Построение сечений

Сечение многогранника

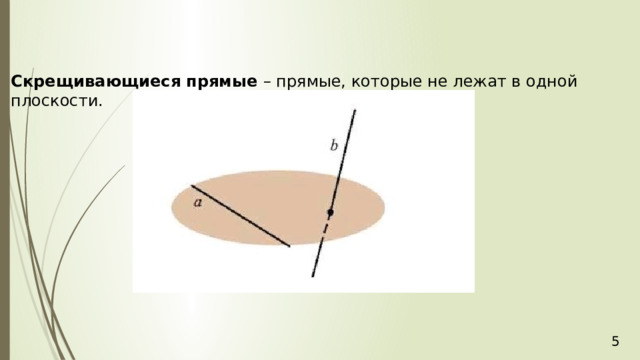
Скрещивающиеся прямые   – прямые, которые не лежат в одной плоскости.

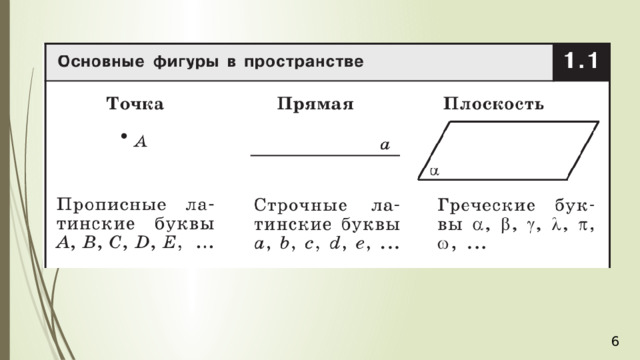
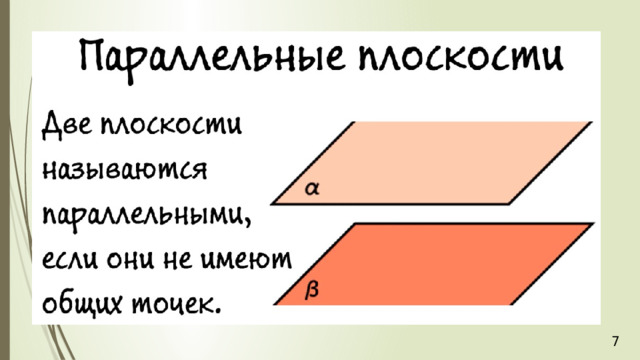
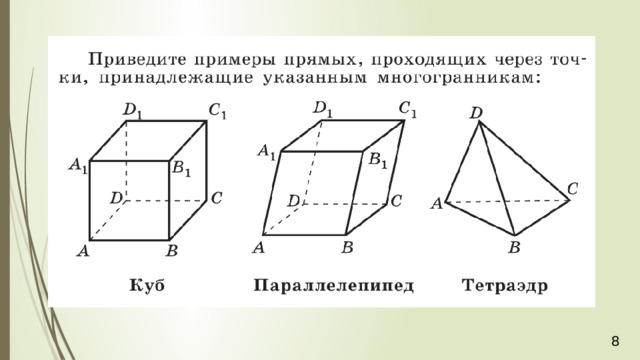
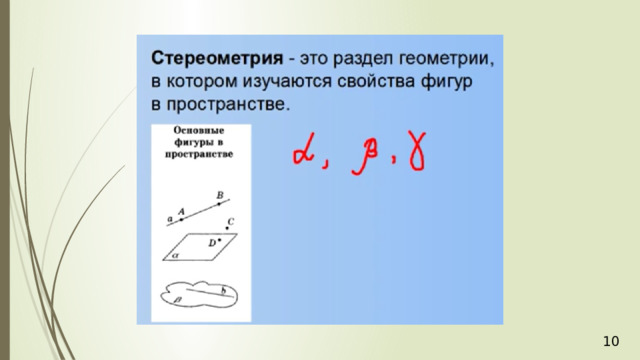
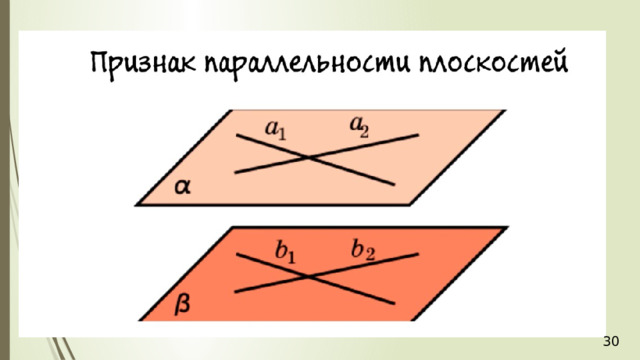
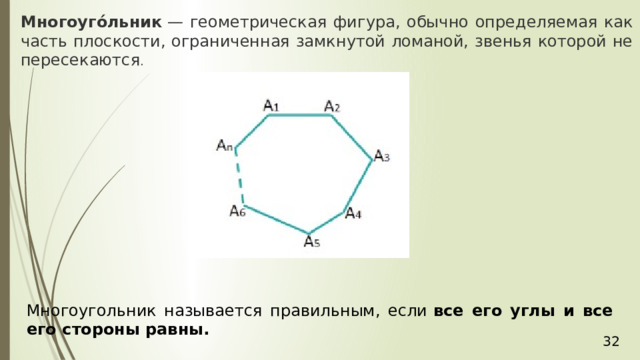
Многоуго́льник  — геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной, звенья которой не пересекаются . 

Многоугольник называется правильным, если  все его углы и все его стороны равны.

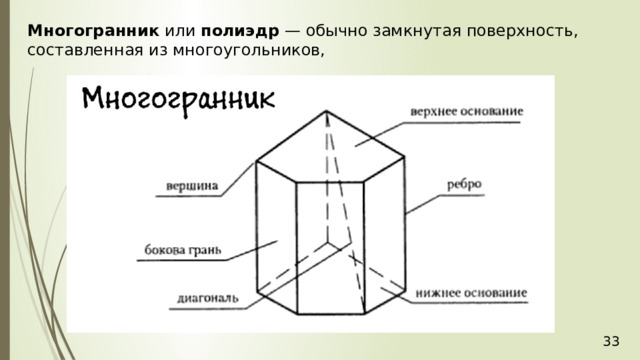
Многогранник  или  полиэдр  — обычно замкнутая поверхность, составленная из многоугольников,

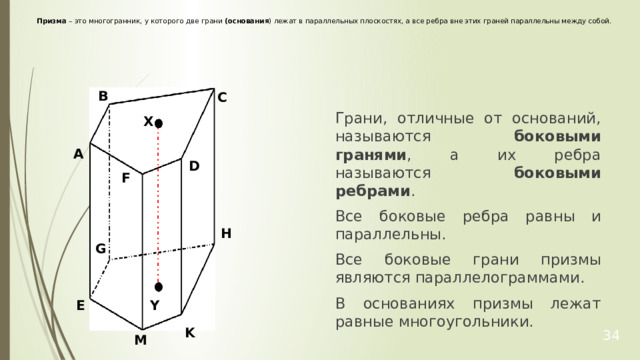
Призма – это многогранник, у которого две грани (основания ) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой.

B

C

Грани, отличные от оснований, называются боковыми гранями , а их ребра называются боковыми ребрами .

Все боковые ребра равны и параллельны.

Все боковые грани призмы являются параллелограммами.

В основаниях призмы лежат равные многоугольники.

X

A

D

A

F

H

G

E

Y

K

34

M

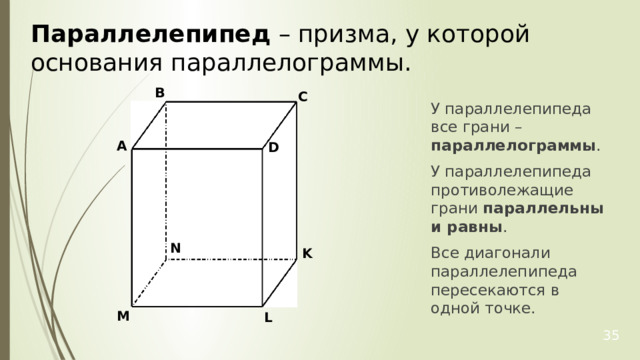
Параллелепипед – призма, у которой основания параллелограммы.

B

C

У параллелепипеда все грани – параллелограммы .

У параллелепипеда противолежащие грани параллельны и равны .

Все диагонали параллелепипеда пересекаются в одной точке.

A

D

N

K

M

L

35

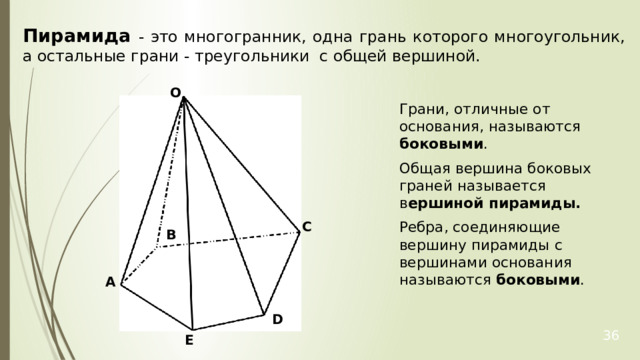
Пирамида - это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной.

O

Грани, отличные от основания, называются боковыми .  

Общая вершина боковых граней называется в ершиной пирамиды.

Ребра, соединяющие вершину пирамиды с вершинами основания называются боковыми .

C

B

A

D

36

E

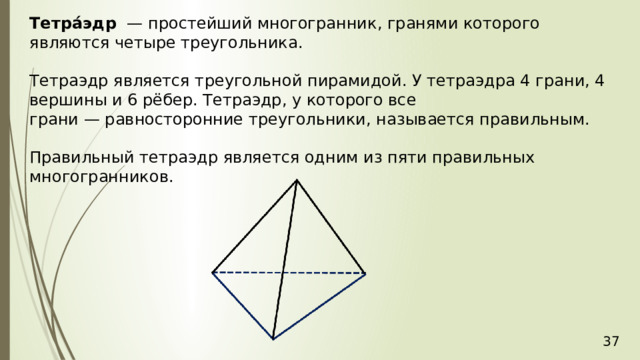
Тетра́эдр   — простейший многогранник, гранями которого являются четыре треугольника.

Тетраэдр является треугольной пирамидой. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным. 

Правильный тетраэдр является одним из пяти правильных многогранников.

36

36

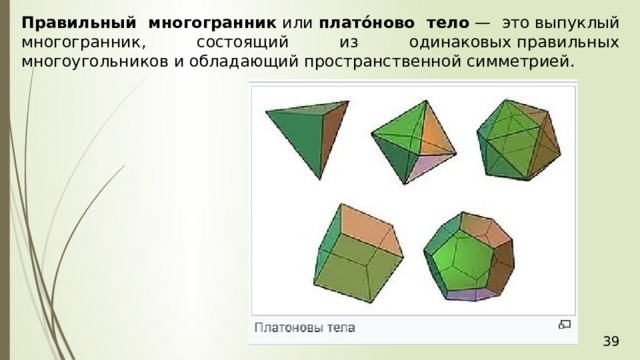
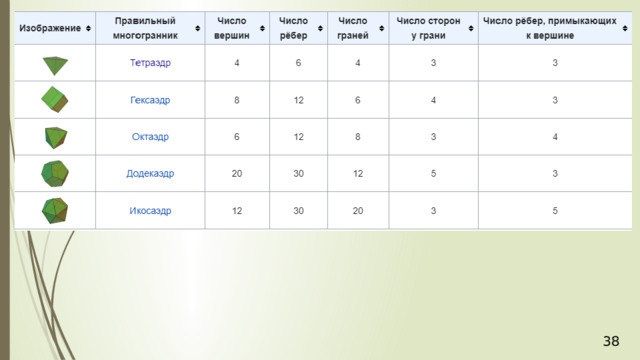
Правильный многогранник  или  плато́ново тело  — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.

36

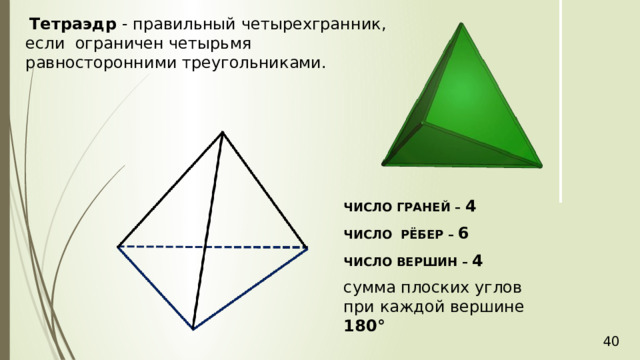
Тетраэдр - правильный четырехгранник, если ограничен четырьмя равносторонними треугольниками.

ЧИСЛО ГРАНЕЙ – 4

ЧИСЛО РЁБЕР – 6

ЧИСЛО ВЕРШИН – 4

сумма плоских углов при каждой вершине 180 °

36

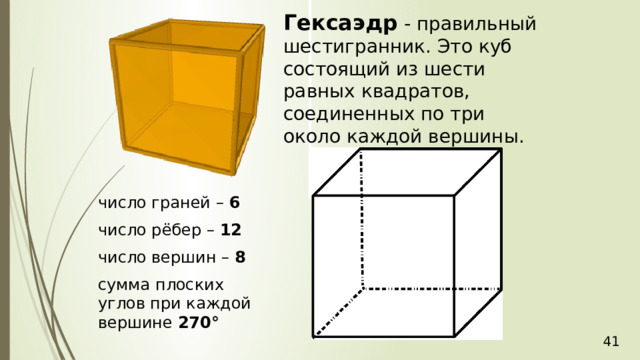
Гексаэдр - правильный шестигранник. Это куб состоящий из шести равных квадратов, соединенных по три около каждой вершины.

число граней – 6

число рёбер – 12

число вершин – 8

сумма плоских углов при каждой вершине 270 °

36

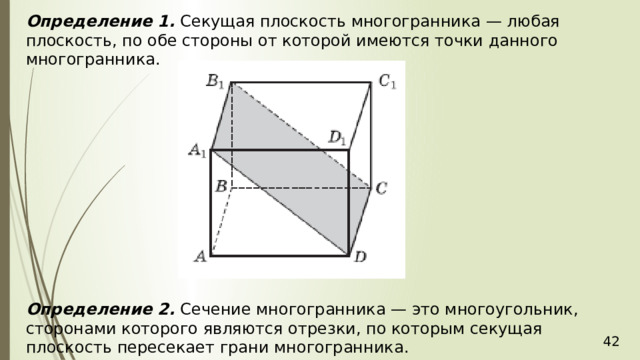
Определение 1.  Секущая плоскость многогранника — любая плоскость, по обе стороны от которой имеются точки данного многогранника.

Определение 2.  Сечение многогранника — это многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани многогранника.

36

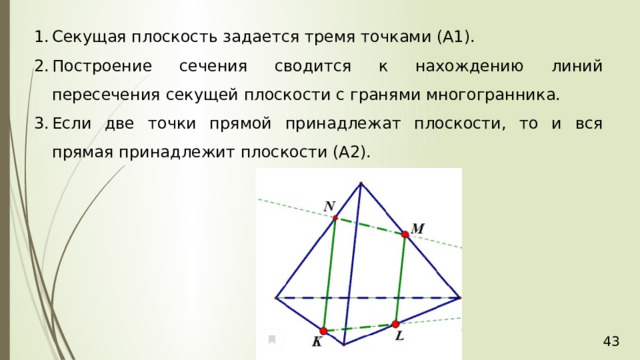
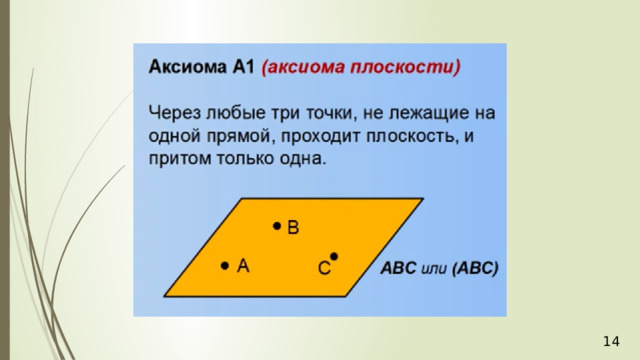
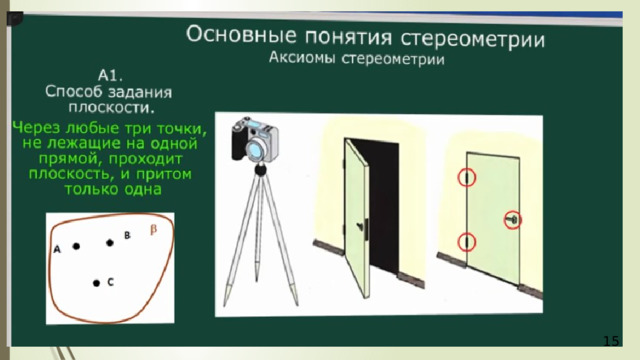
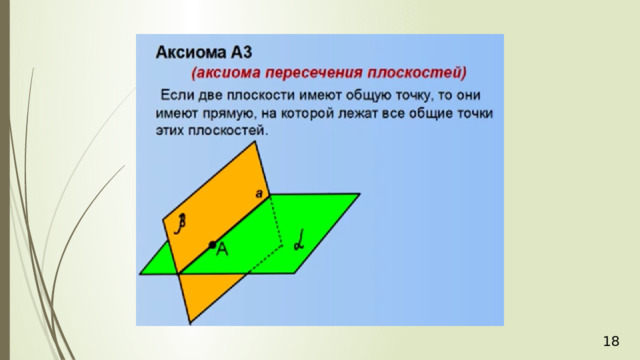
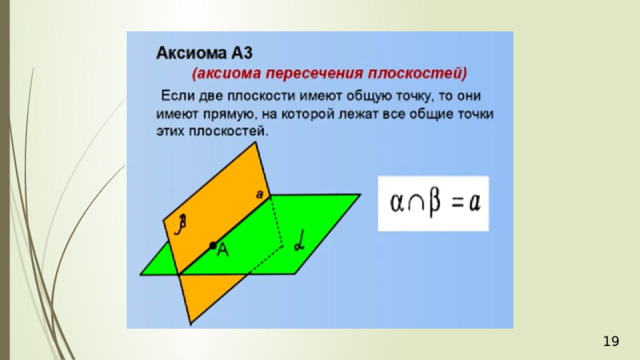
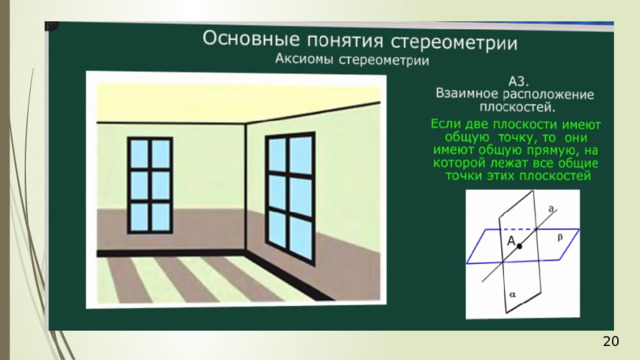
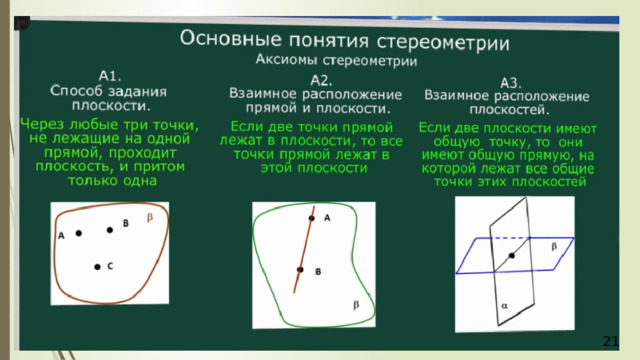
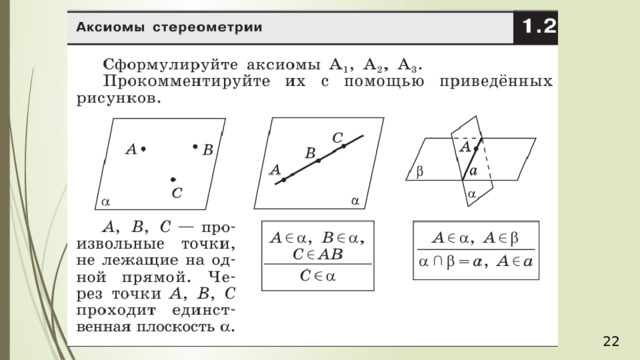
• Секущая плоскость задается тремя точками (А1).
• Построение сечения сводится к нахождению линий пересечения секущей плоскости с гранями многогранника.
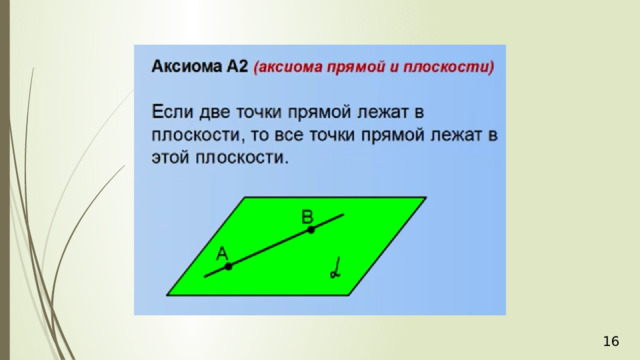
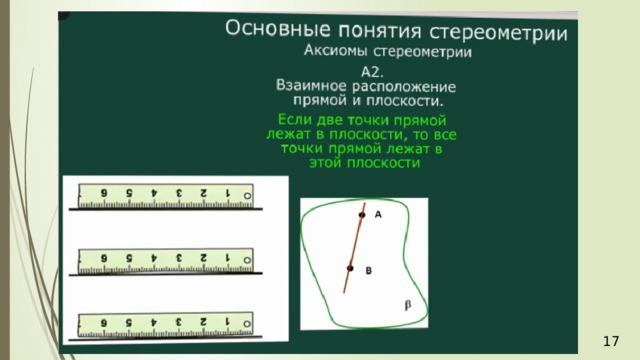
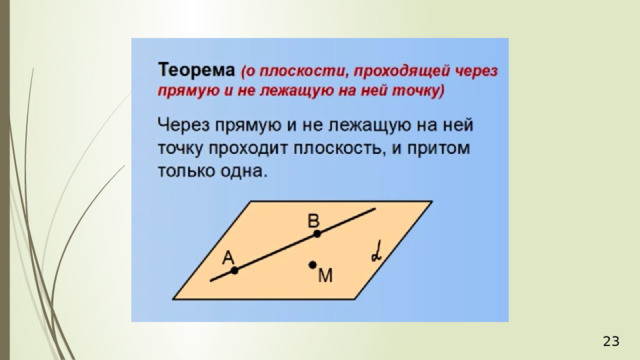
• Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости (А2).

36

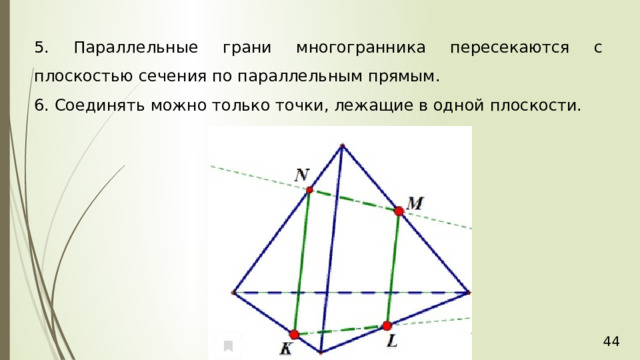
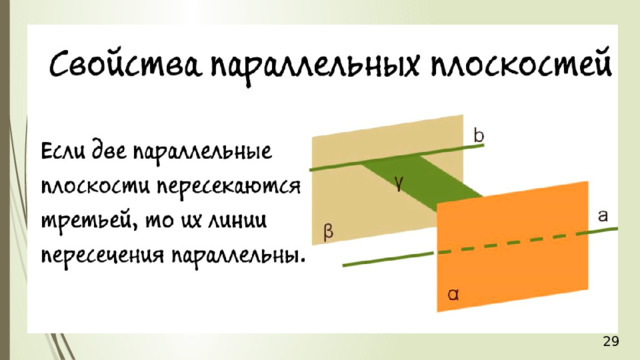
5. Параллельные грани многогранника пересекаются с плоскостью сечения по параллельным прямым .

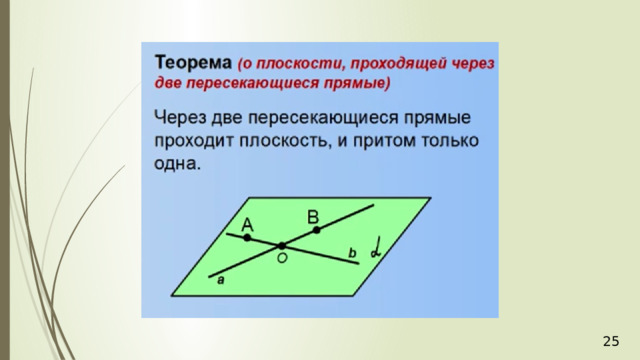
6. Соединять можно только точки, лежащие в одной плоскости.

36

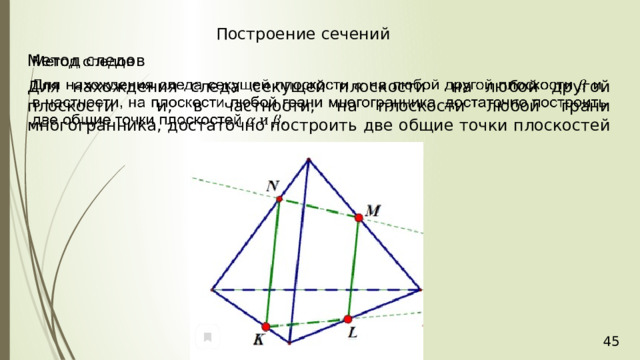
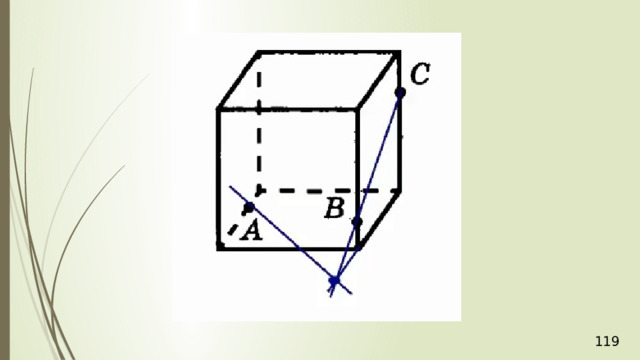
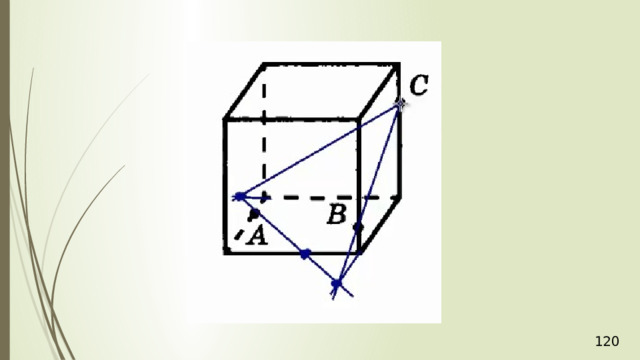
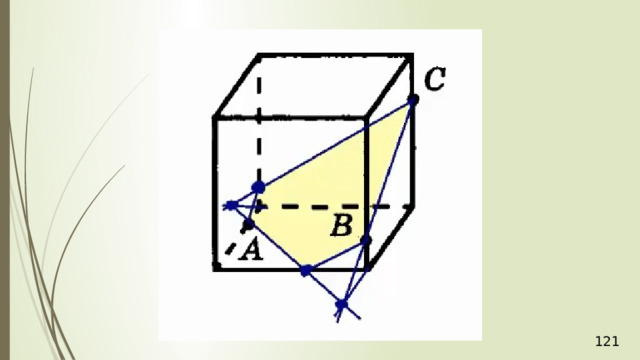
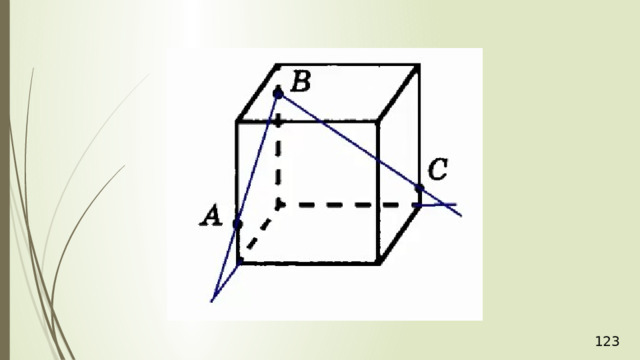
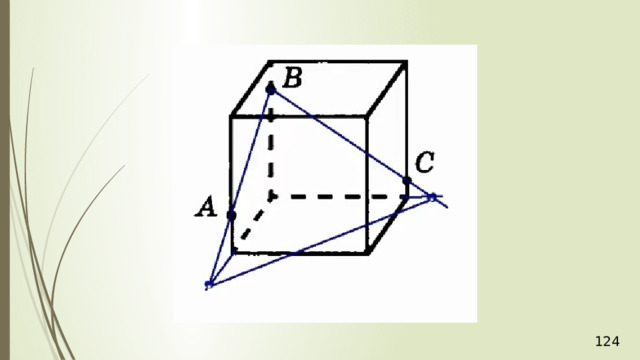
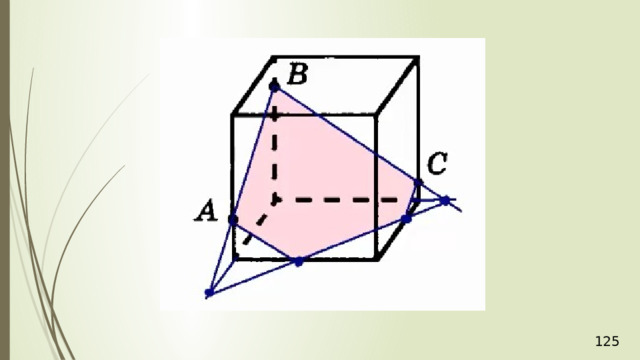
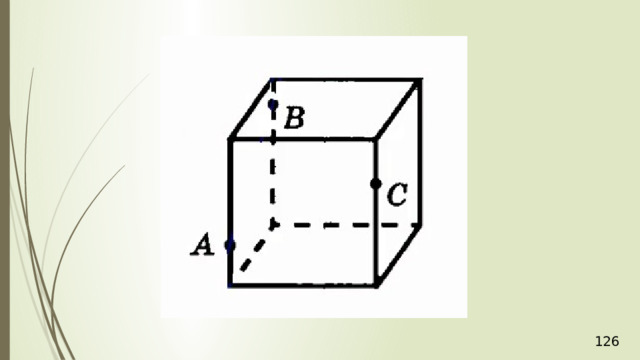
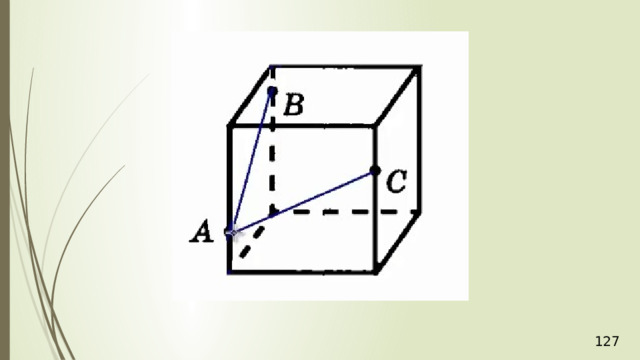
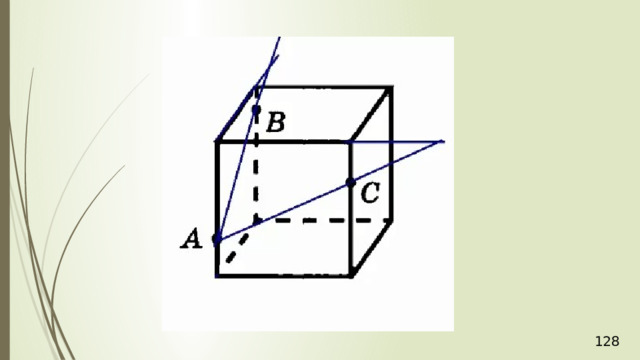
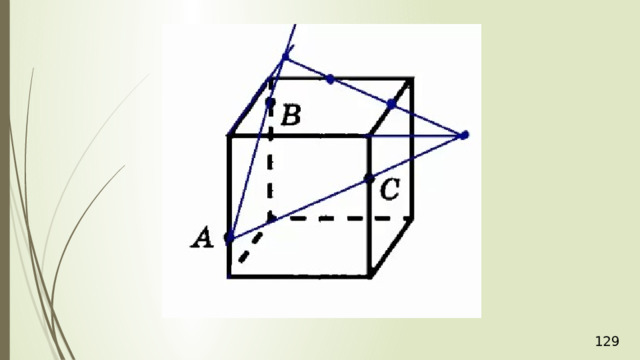
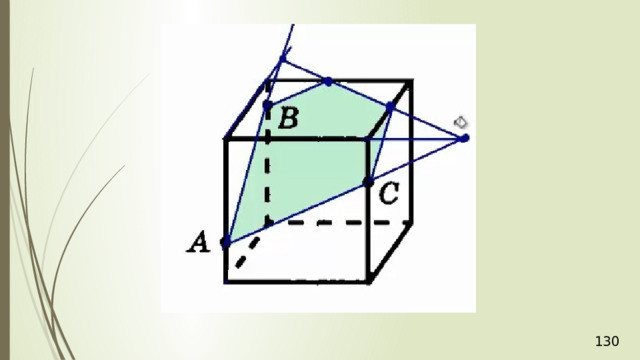
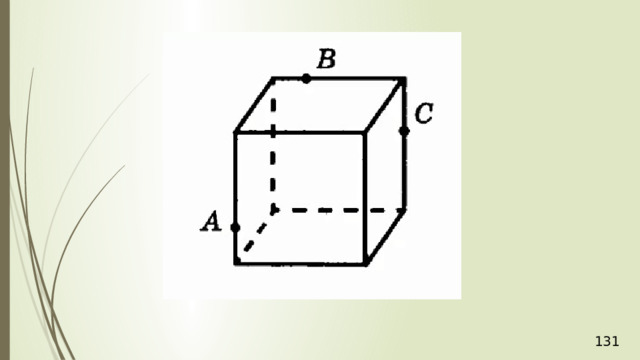
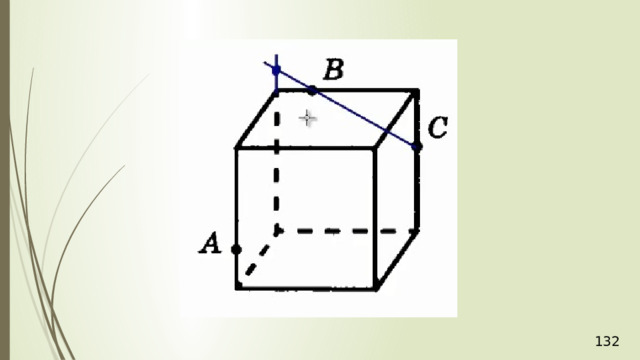
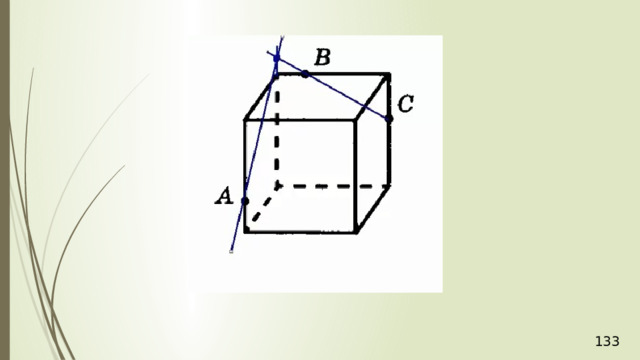
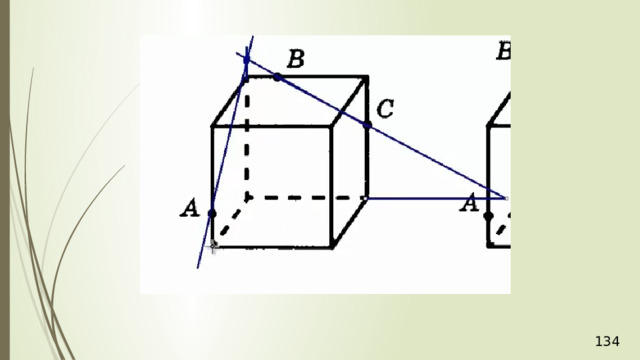
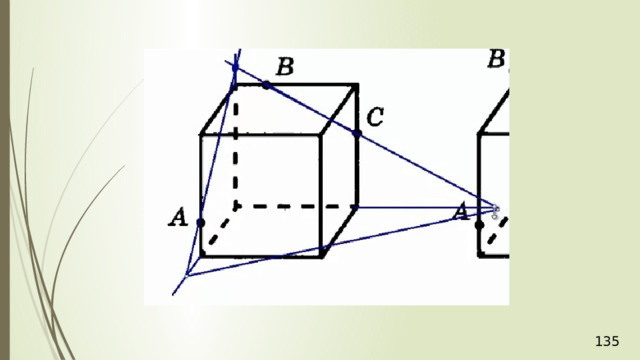
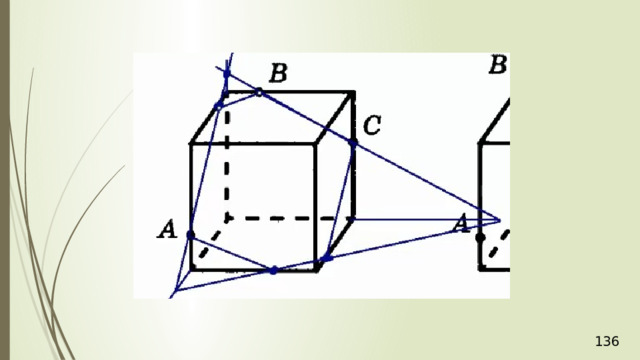
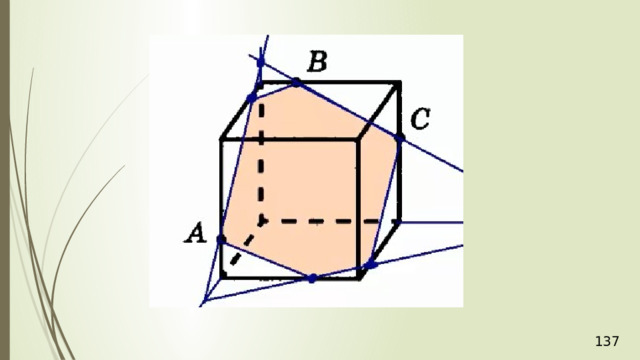
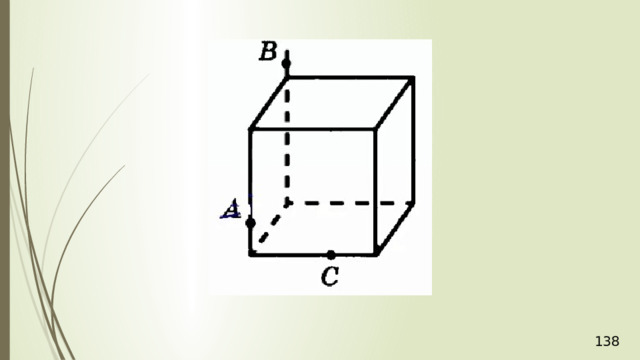
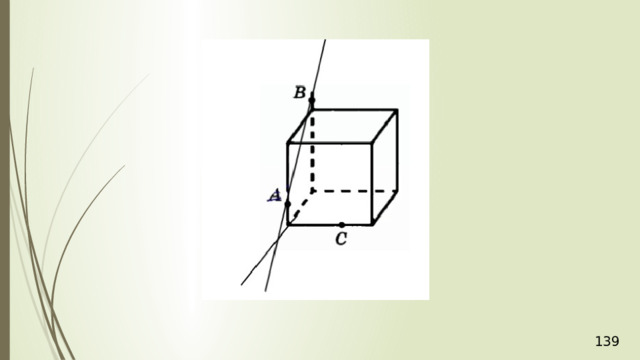
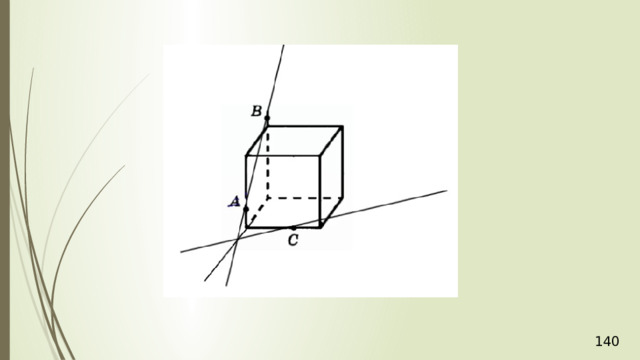
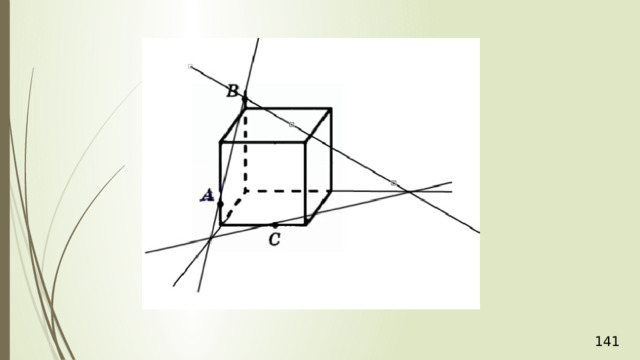
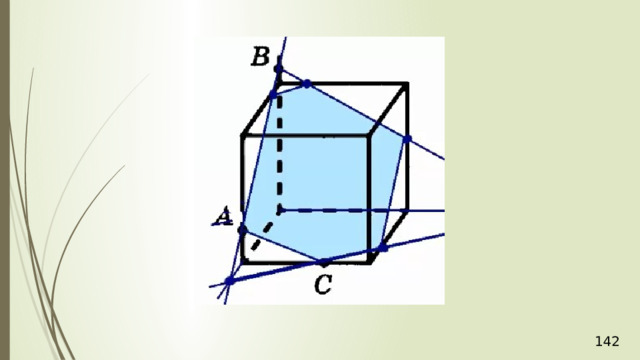
Построение сечений

Метод следов

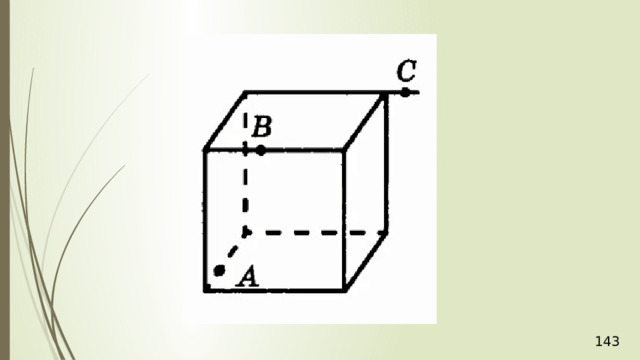
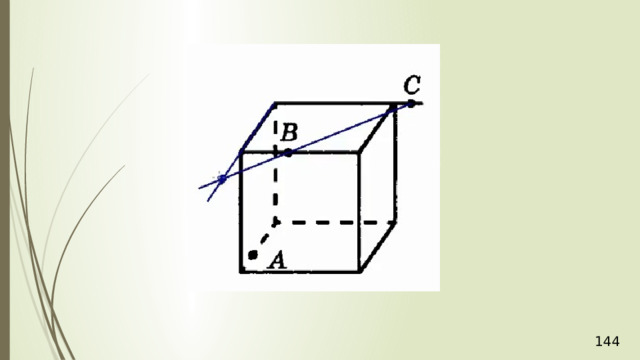
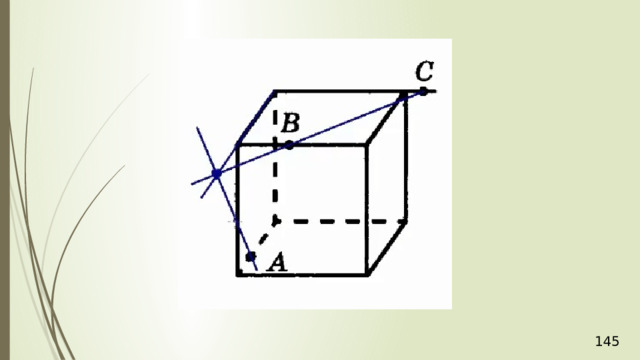
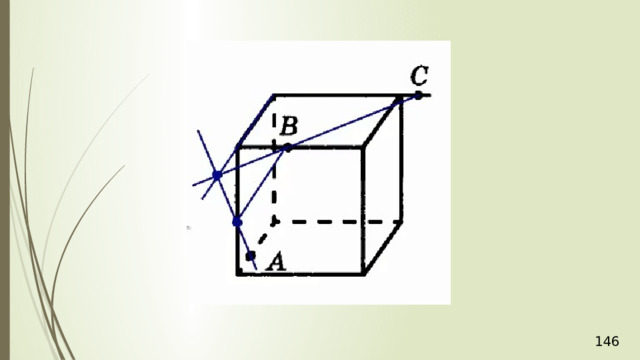
Для нахождения следа секущей плоскости на любой другой плоскости и, в частности, на плоскости любой грани многогранника, достаточно построить две общие точки плоскостей

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

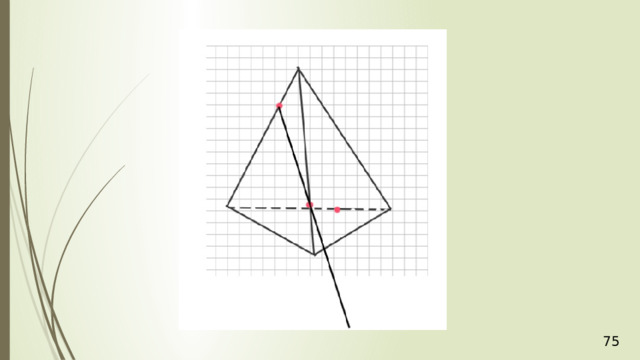
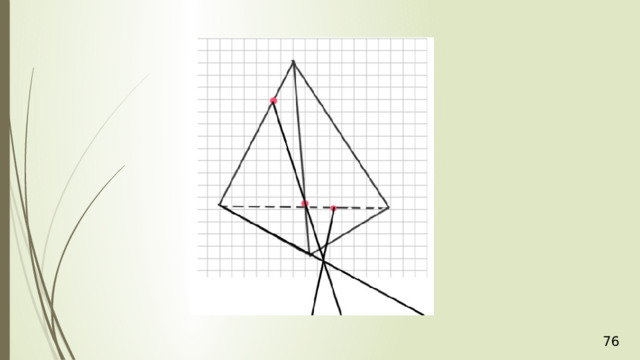
Е

D

К

36

36

36

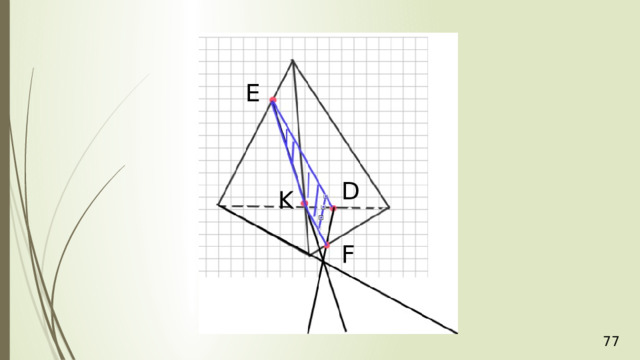
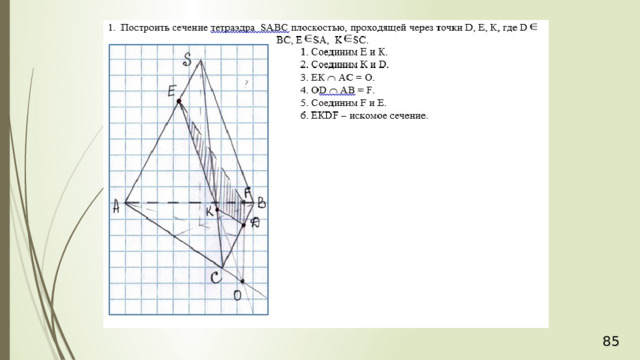
Е

D

K

F

36

36

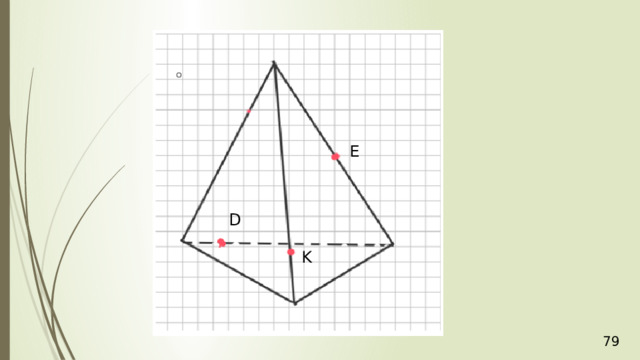
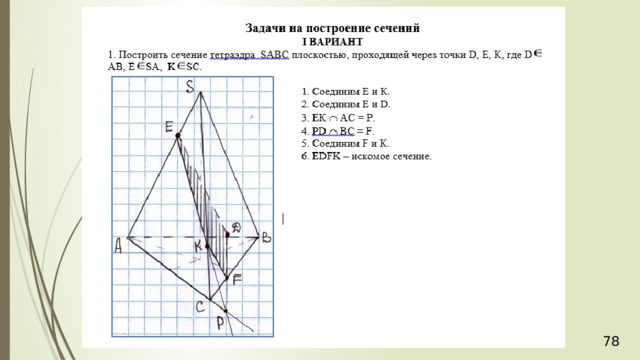
E

D

K

36

36

36

36

36

36

36

36

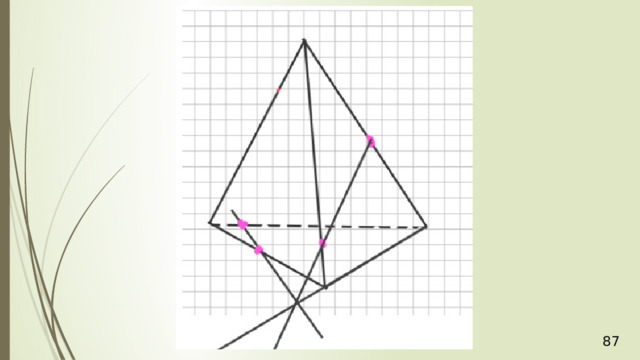
36

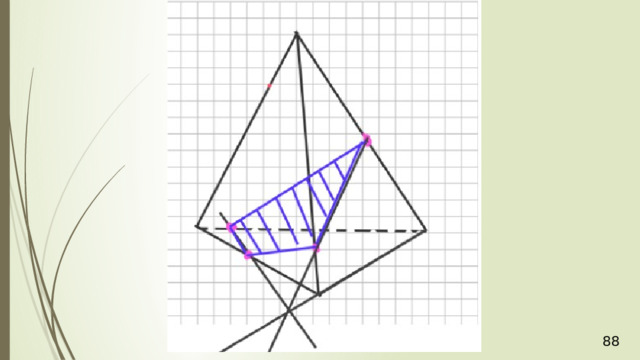
36

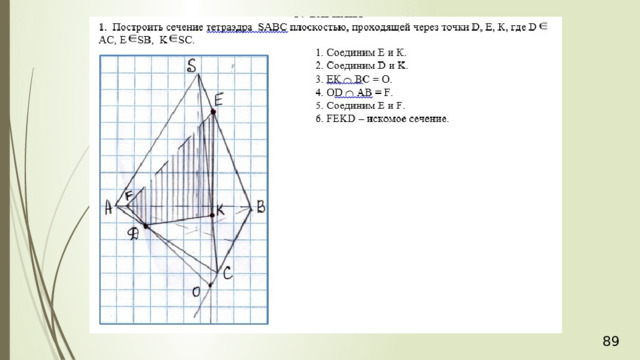
36

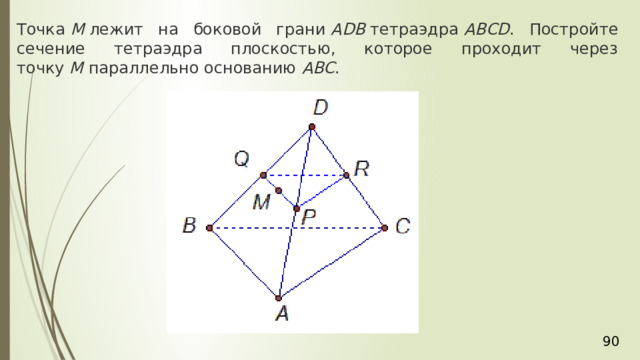
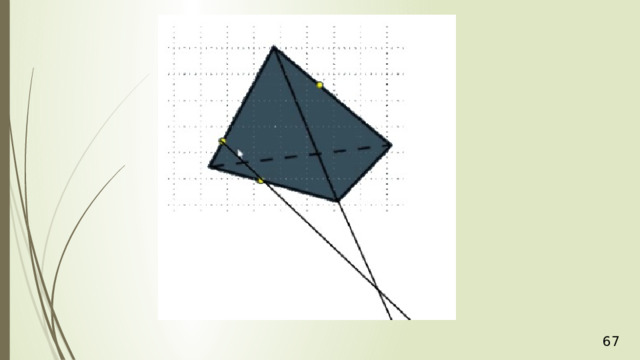
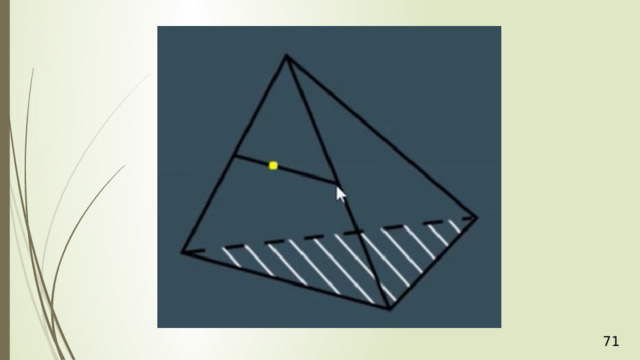
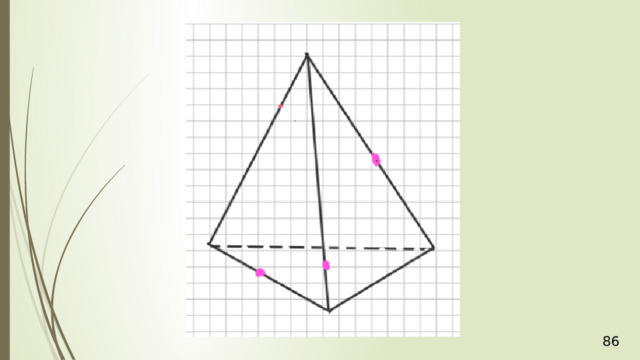
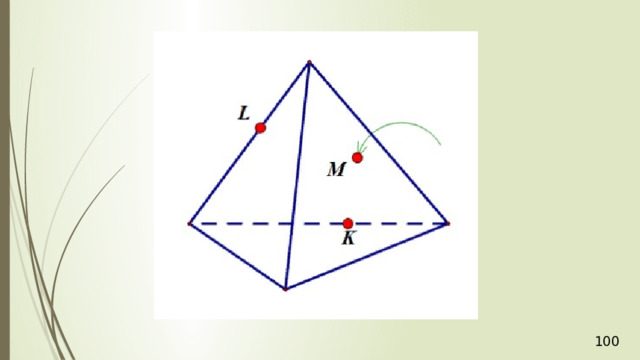
Точка  М  лежит на боковой грани  АDВ  тетраэдра  АВСD . Постройте сечение тетраэдра плоскостью, которое проходит через точку  М  параллельно основанию  АВС .

36

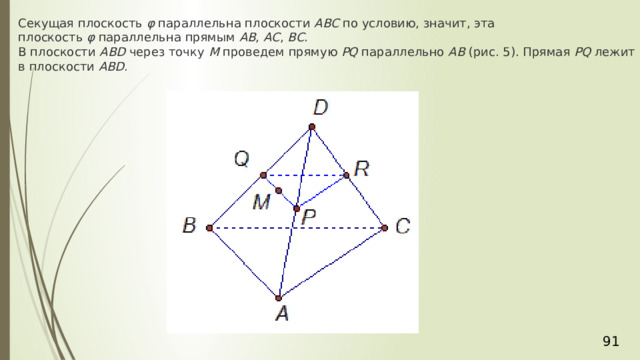
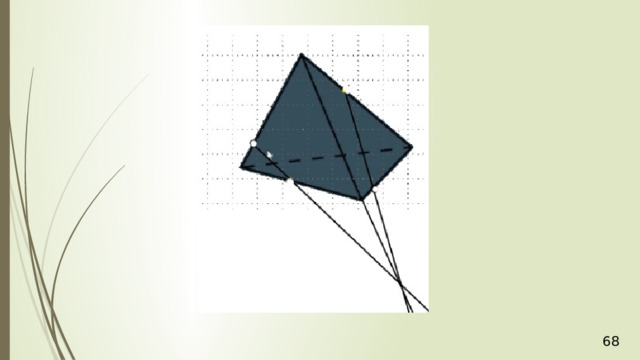
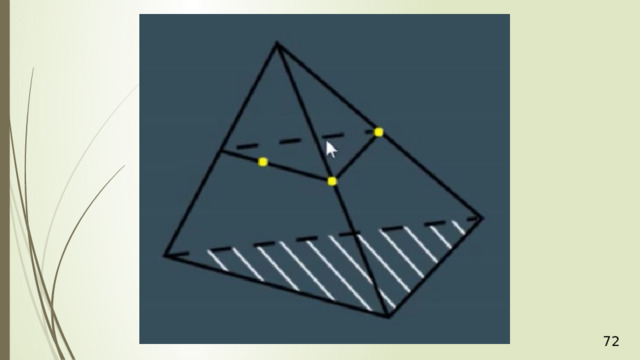
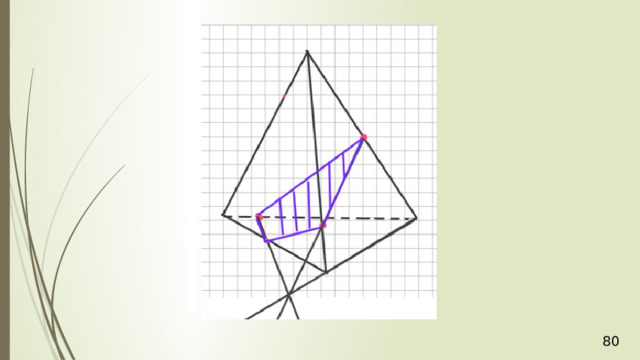
Секущая плоскость  φ  параллельна плоскости  АВС  по условию, значит, эта плоскость  φ  параллельна прямым  АВ ,  АС ,  ВС .  В плоскости  АВD  через точку  М  проведем прямую  PQ  параллельно  АВ  (рис. 5). Прямая  PQ  лежит в плоскости  АВD .

36

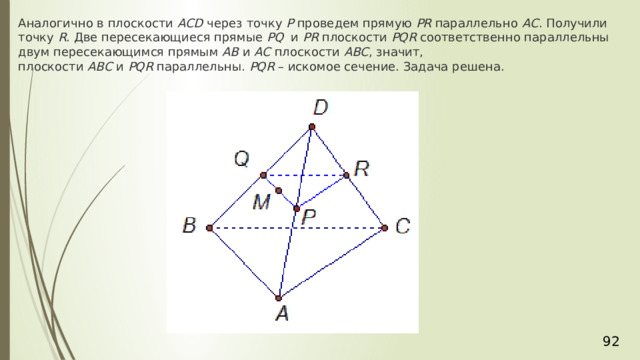
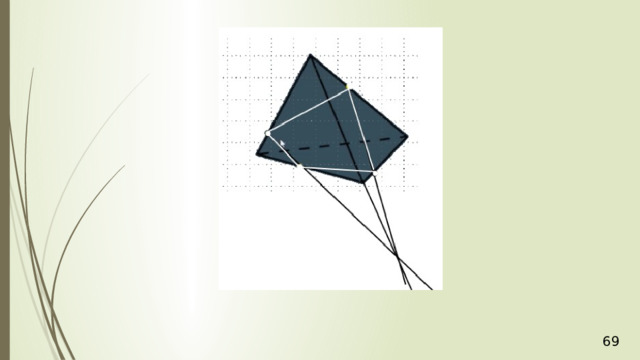
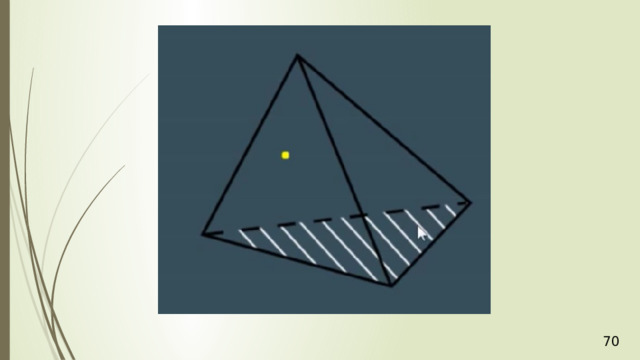
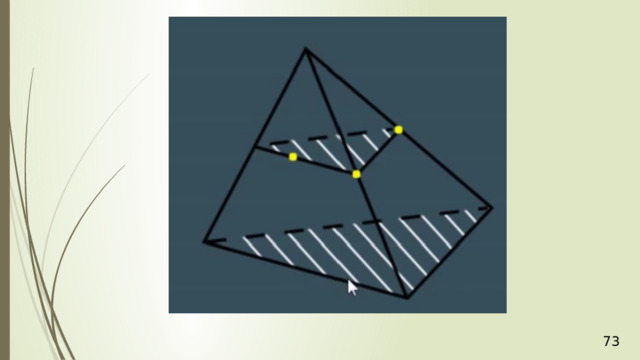
Аналогично в плоскости  АСD  через точку  Р  проведем прямую  РR  параллельно  АС . Получили точку  R . Две пересекающиеся прямые  PQ   и  РR  плоскости  РQR  соответственно параллельны двум пересекающимся прямым  АВ  и  АС  плоскости  АВС , значит, плоскости  АВС  и  РQR  параллельны.  РQR  – искомое сечение. Задача решена.

36

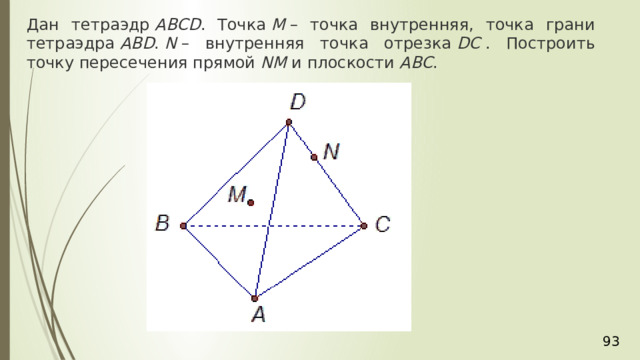
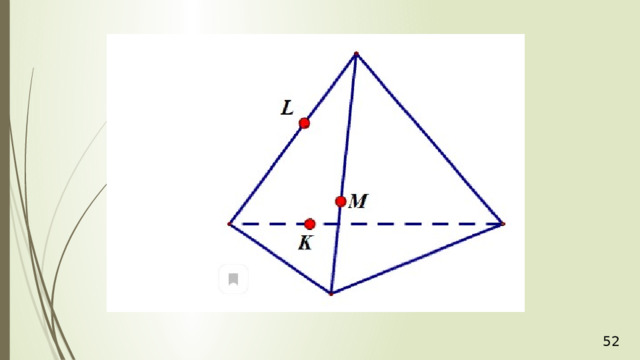
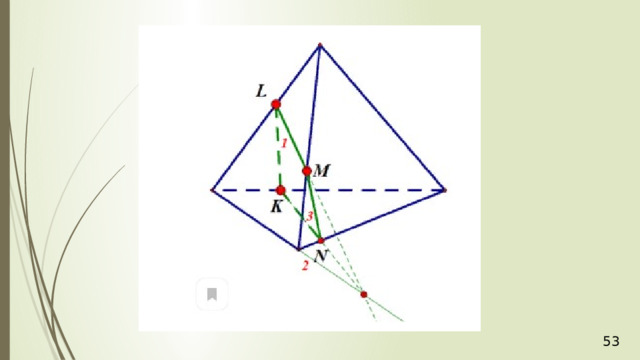
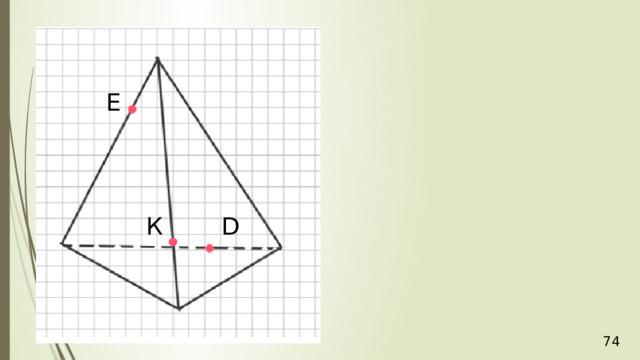
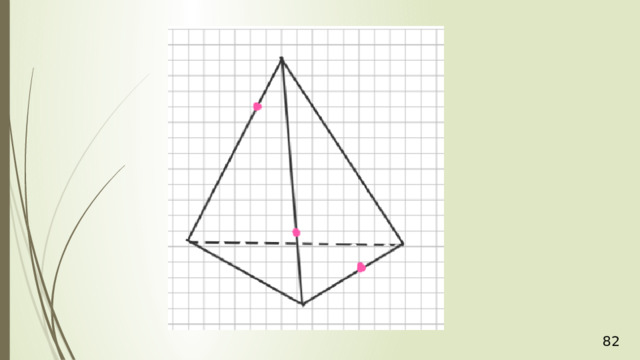
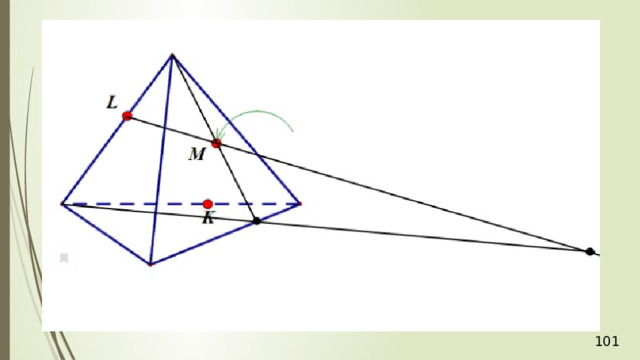
Дан тетраэдр  АВСD . Точка  М  – точка внутренняя, точка грани тетраэдра  АВD .  N  – внутренняя точка отрезка  DС  . Построить точку пересечения прямой  NM  и плоскости  АВС .

36

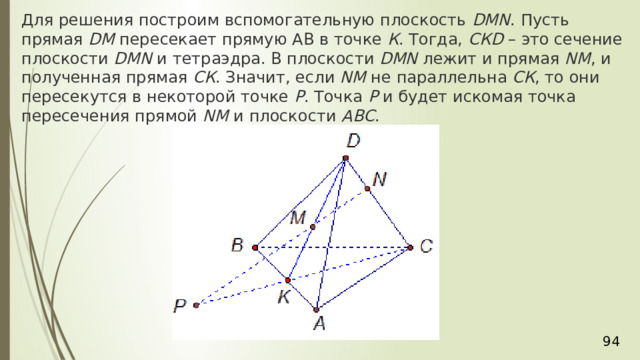
Для решения построим вспомогательную плоскость  DМN . Пусть прямая  DМ  пересекает прямую АВ в точке  К . Тогда,  СКD  – это сечение плоскости  DМN  и тетраэдра. В плоскости  DМN  лежит и прямая  NM , и полученная прямая  СК . Значит, если  NM  не параллельна  СК , то они пересекутся в некоторой точке  Р . Точка  Р  и будет искомая точка пересечения прямой  NM  и плоскости  АВС .

36

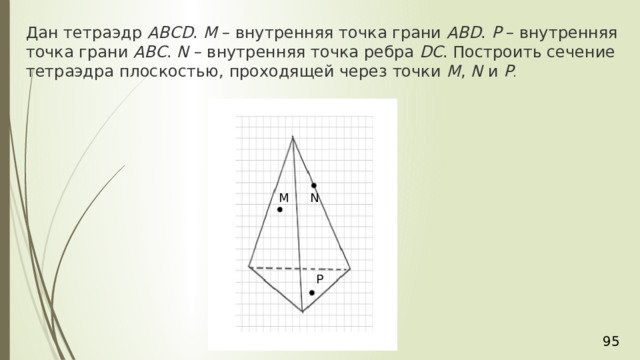
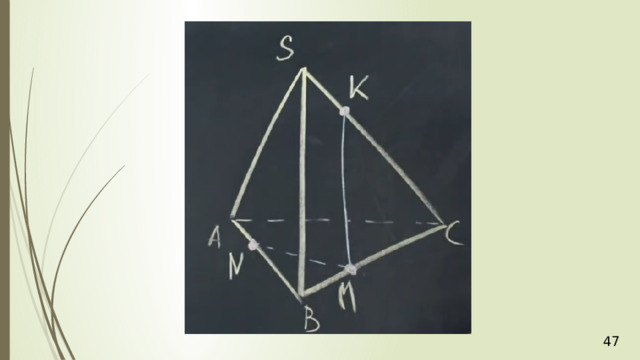
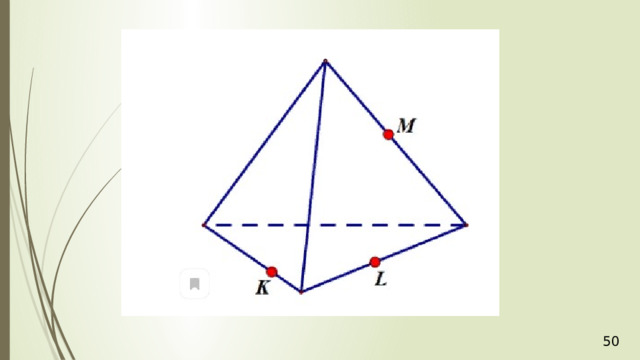
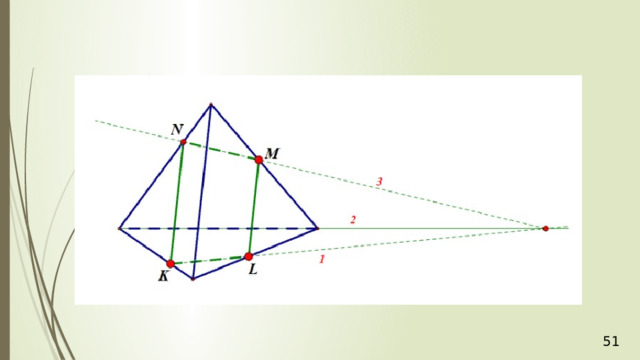
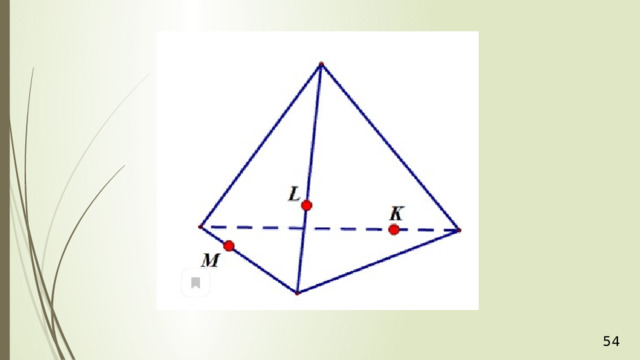
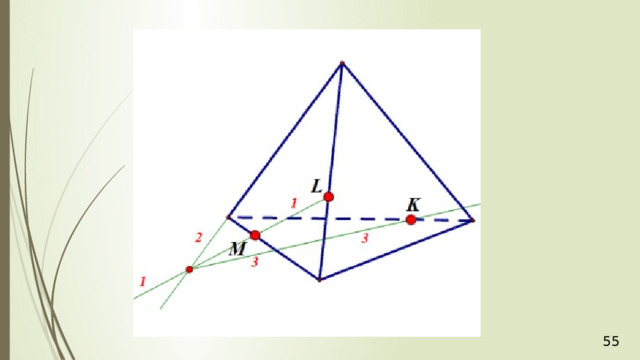
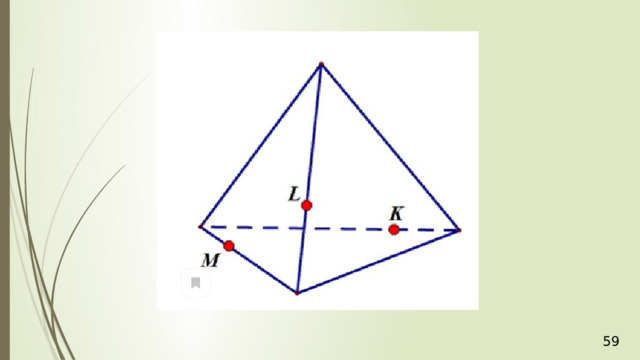
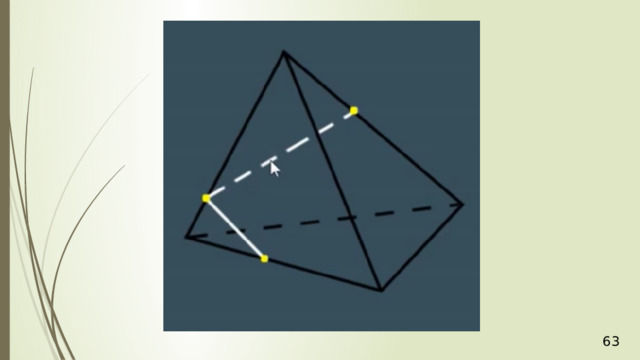
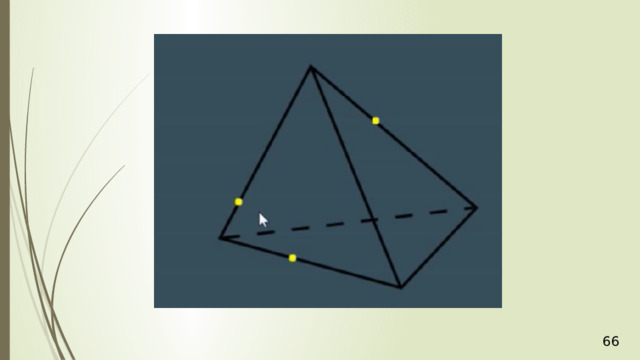
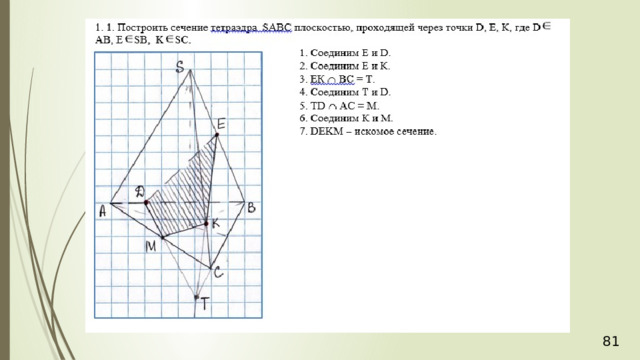
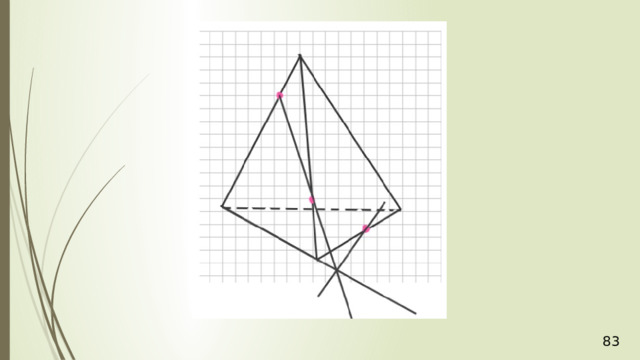
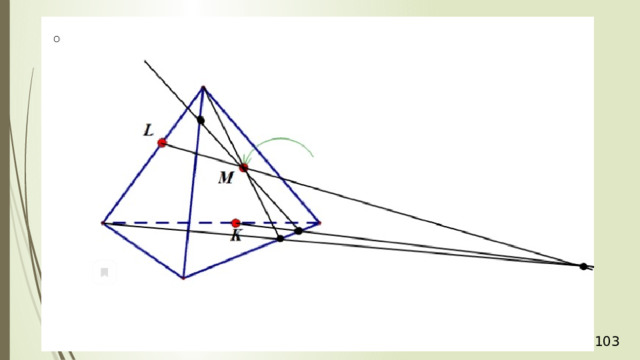
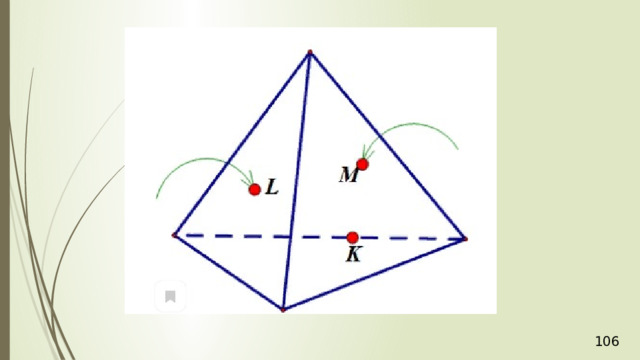
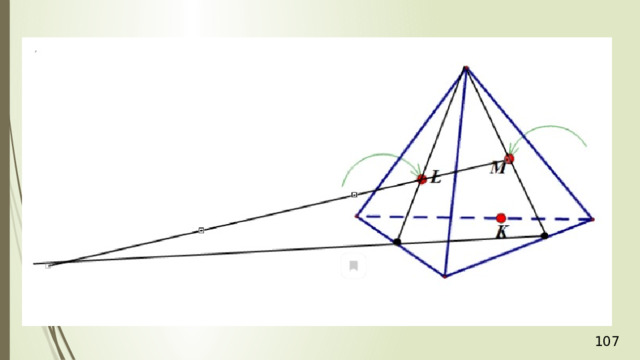
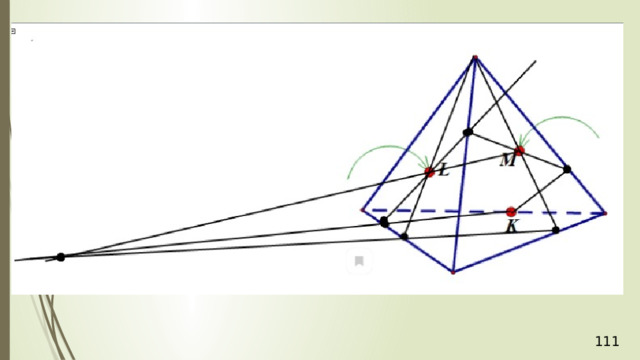
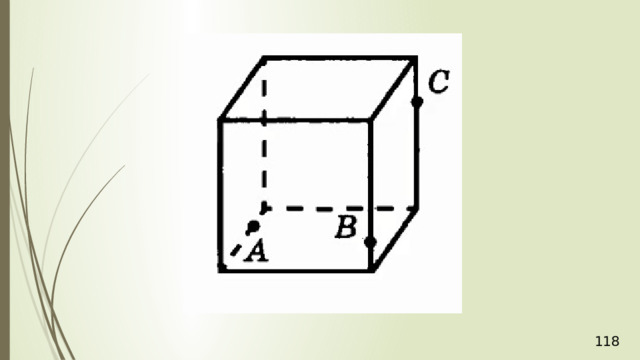
Дан тетраэдр  АВСD .  М  – внутренняя точка грани  АВD .  Р  – внутренняя точка грани  АВС .  N  – внутренняя точка ребра  DС . Построить сечение тетраэдра плоскостью, проходящей через точки  М ,  N  и  Р .

N

М

P

36

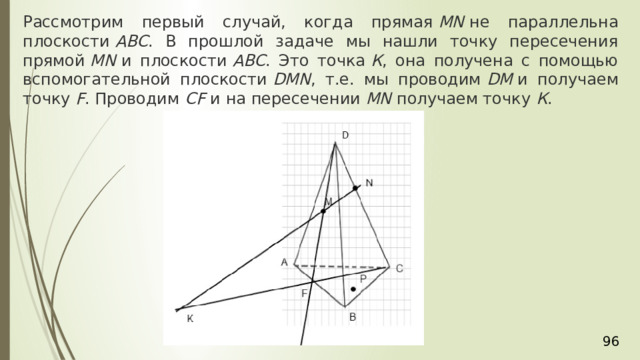
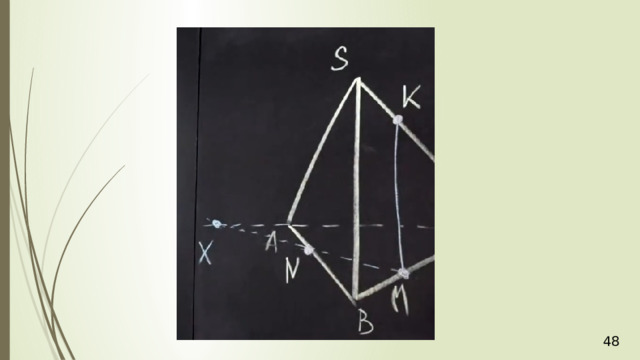
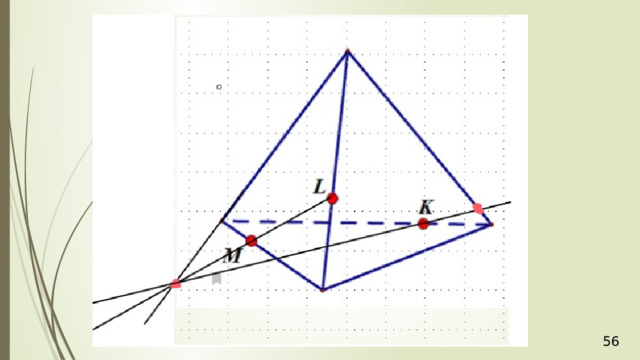
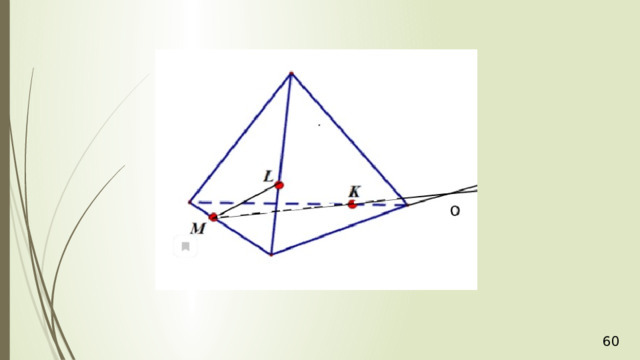
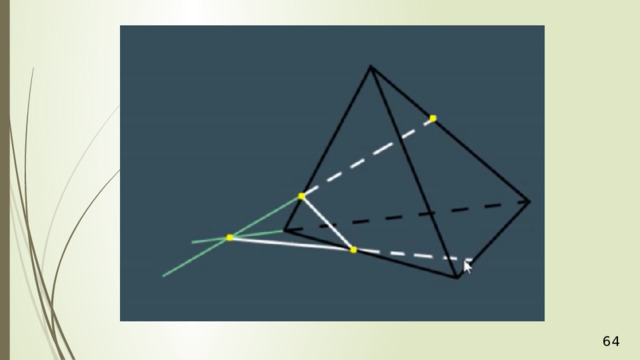
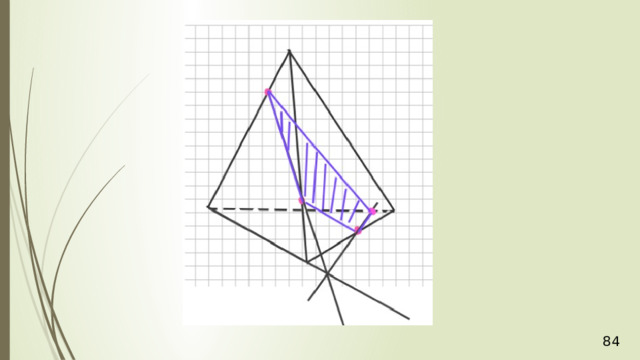
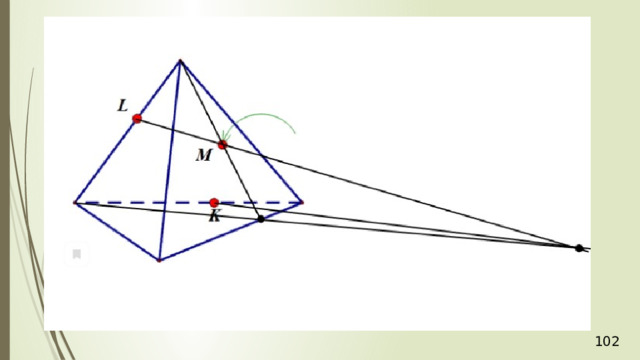
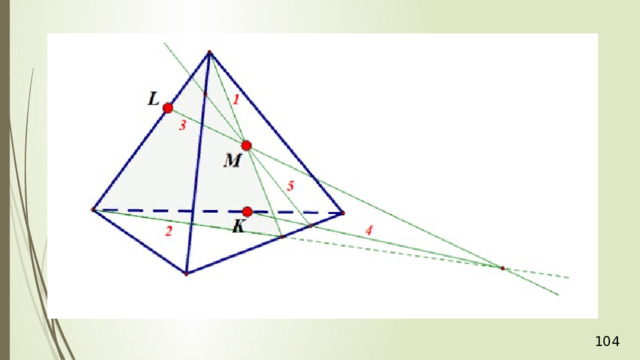
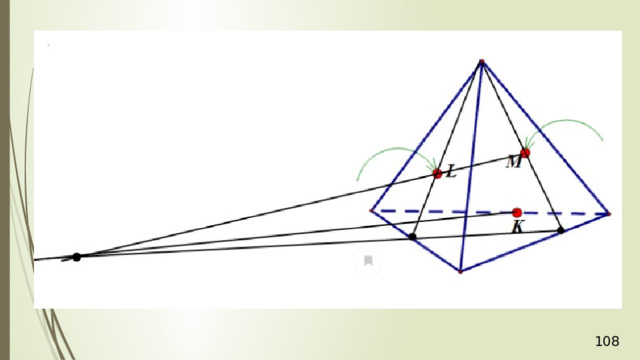
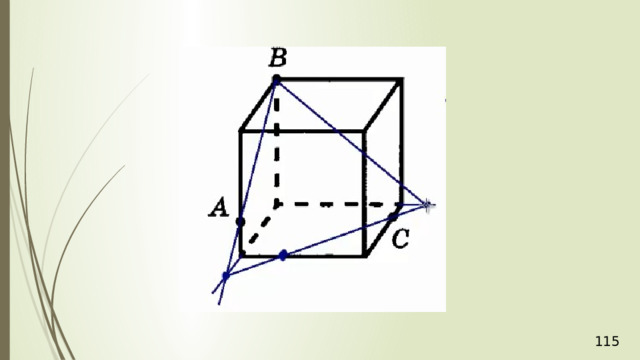
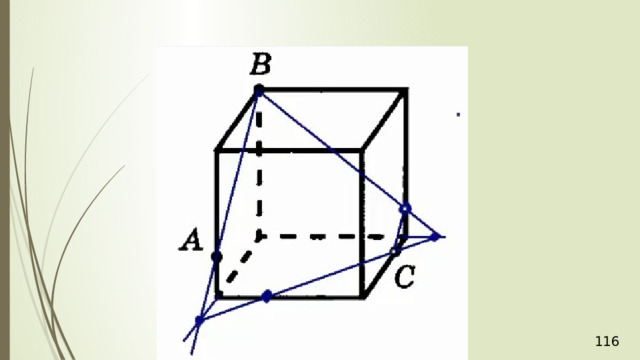
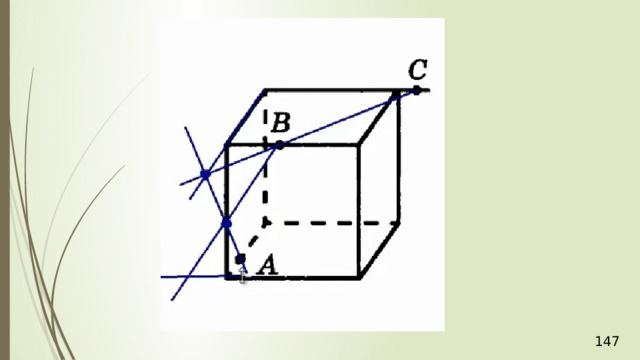
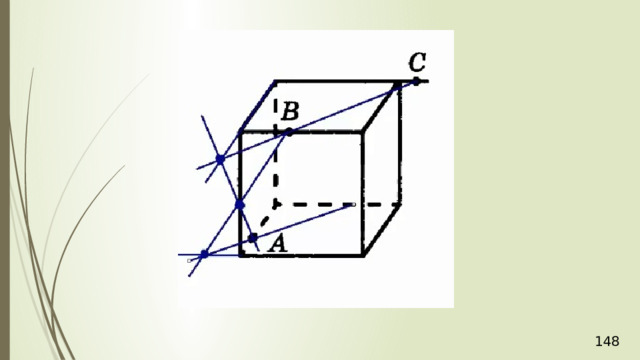
Рассмотрим первый случай, когда прямая  MN  не параллельна плоскости  АВС . В прошлой задаче мы нашли точку пересечения прямой  MN  и плоскости  АВС . Это точка  К , она получена с помощью вспомогательной плоскости  DМN , т.е. мы проводим  DМ  и получаем точку  F . Проводим  СF  и на пересечении  MN  получаем точку  К .

36

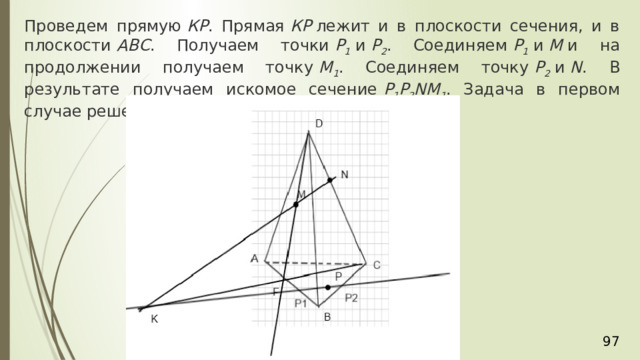
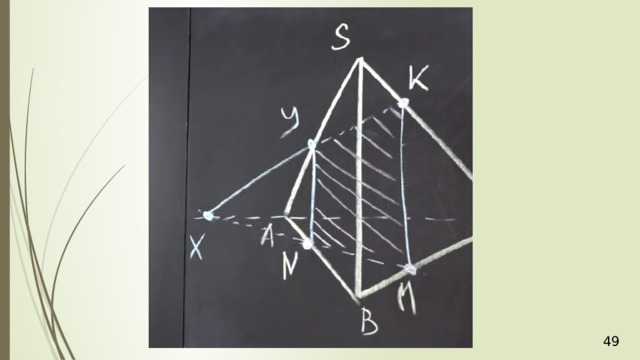
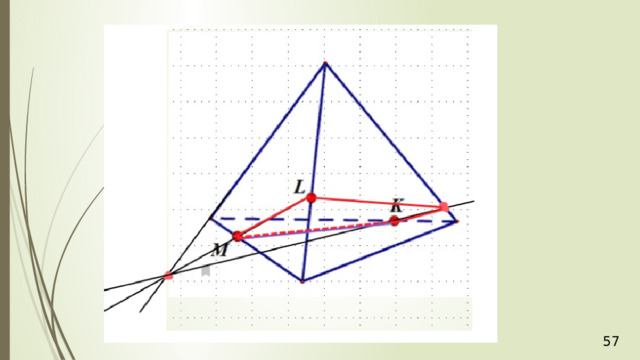
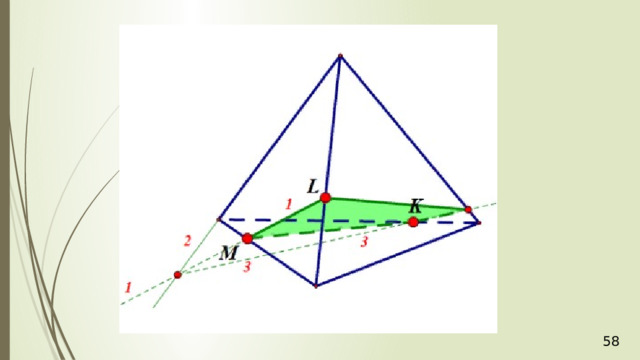
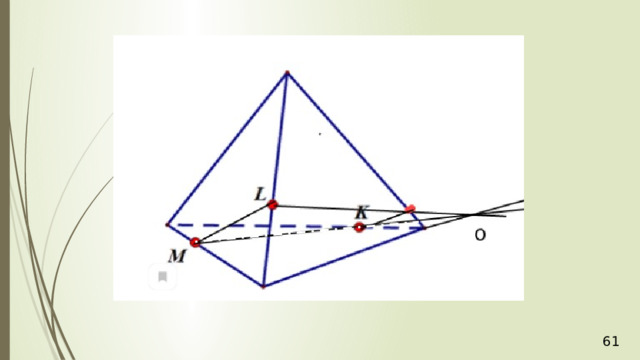
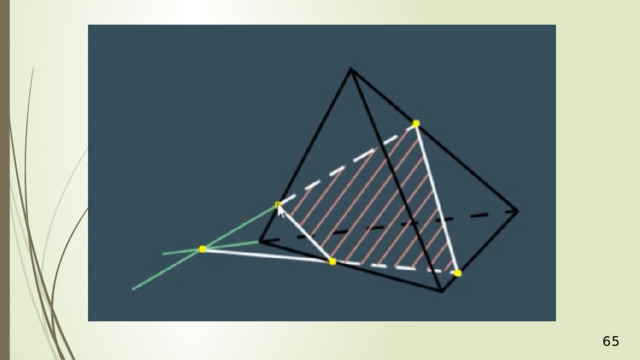
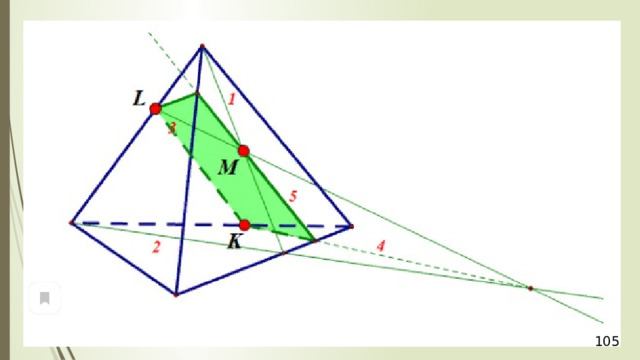
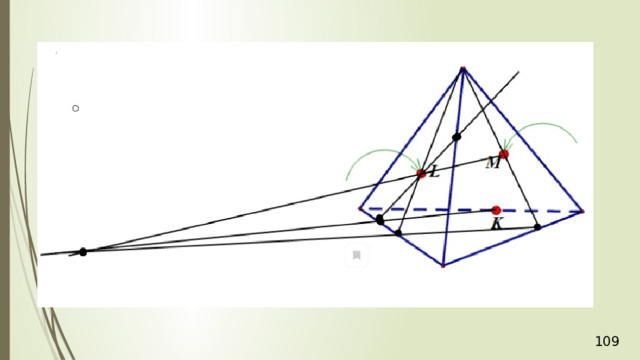
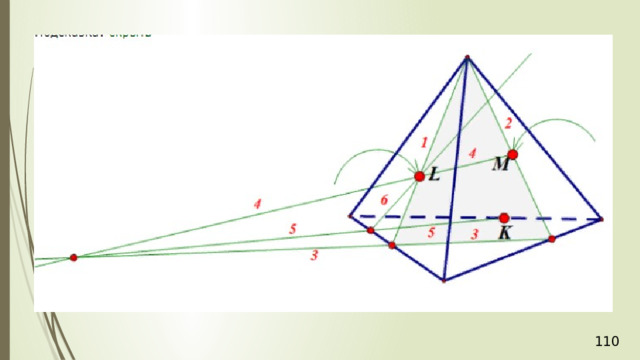
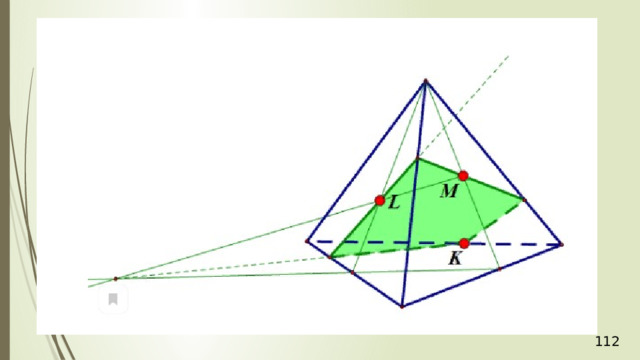
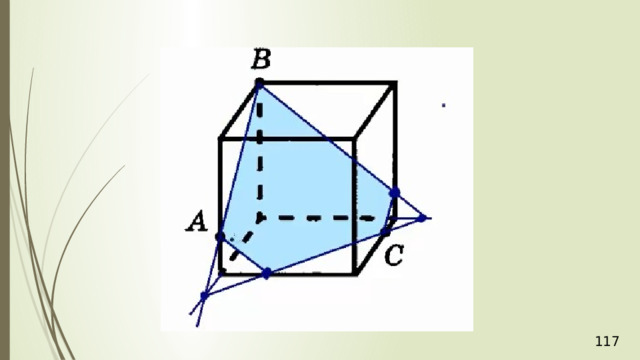
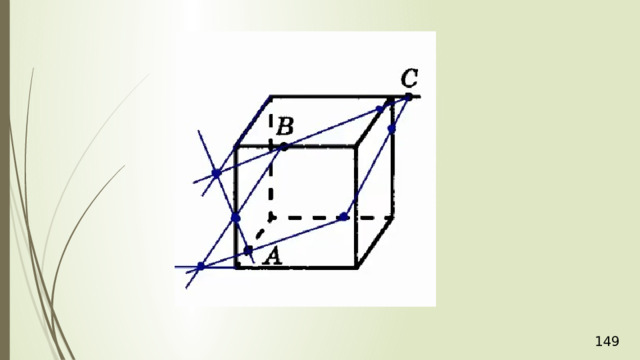
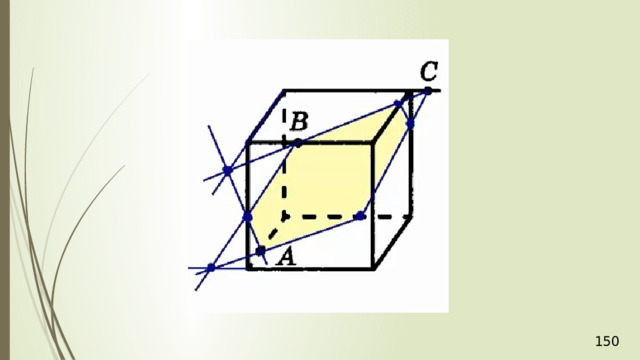
Проведем прямую  КР . Прямая  КР  лежит и в плоскости сечения, и в плоскости  АВС . Получаем точки  Р 1  и  Р 2 . Соединяем  Р 1  и  М  и на продолжении получаем точку  М 1 . Соединяем точку  Р 2  и  N . В результате получаем искомое сечение  Р 1 Р 2 NМ 1 . Задача в первом случае решена.

36

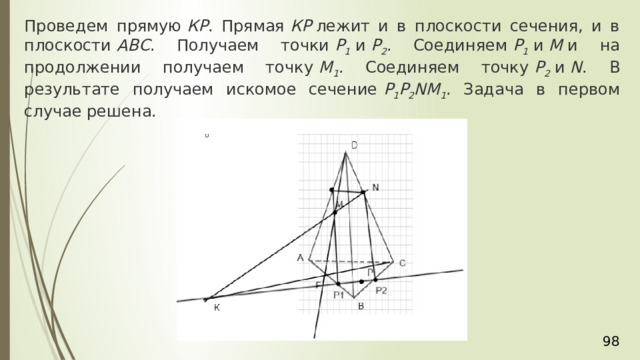
Проведем прямую  КР . Прямая  КР  лежит и в плоскости сечения, и в плоскости  АВС . Получаем точки  Р 1  и  Р 2 . Соединяем  Р 1  и  М  и на продолжении получаем точку  М 1 . Соединяем точку  Р 2  и  N . В результате получаем искомое сечение  Р 1 Р 2 NМ 1 . Задача в первом случае решена.

36

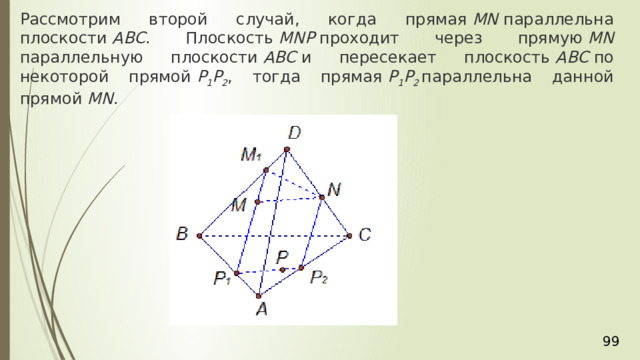
Рассмотрим второй случай, когда прямая  MN  параллельна плоскости  АВС . Плоскость  МNР  проходит через прямую  МN параллельную плоскости  АВС  и пересекает плоскость  АВС  по некоторой прямой  Р 1 Р 2 , тогда прямая  Р 1 Р 2  параллельна данной прямой  MN .

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36

36