Функции, графики и их свойства встречаются в школьном курсе математики на протяжении всей основной и старшей школы. В основной школе рассматриваются линейные, квадратичные, степенные функции, функции обратной пропорциональности, иррациональные функции и функции, содержащие модуль. Данные функции встречаются в заданиях №11 и №22 основного государственного экзамена по математике.
Для качественного освоения данного материала рекомендуется изучать его в предложенном порядке, поскольку каждая последующая тема включает в себя предыдущие, и задачи расположены от простой к сложной.
Оглавление
1.Общие сведения о функции 3
2. Линейная функция 5
3.Квадратичная функция 17
3.Функция 𝑦=𝑘𝑥 25
4.Функция 𝑦=𝑥 33
5.Функции, содержащие знак модуля 39
6.Кусочно-непрерывные функции 48
7.Нахождение наименьшего и наибольшего значения 55
Ответы к практикумам по заданиям из ОГЭ 58
Список литературы 60
1.Общие сведения о функции
Функция – это одно из важнейших математических понятий. Функция – зависимость переменной 𝑦 от переменной 𝑥, если каждому значению 𝑥 соответствует единственное значение 𝑦. Переменную 𝑥 называют независимой переменной или аргументом. Переменную 𝑦 называют зависимой переменной.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции, то есть по оси абсцисс откладываются значения переменной x, а по оси ординат откладываются значения переменной y. Для построения графика функции необходимо знать свойства функции.
Основные свойства функций
Область определения функции – это множество всех допустимых действительных значений аргумента 𝑥 (переменной 𝑥), при которых функция 𝑦 = 𝑓(𝑥) определена.
Область значений функции – это множество всех действительных значений 𝑦, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
Монотонность функции.
Возрастающая функция (в некотором промежутке) – функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) – функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Четность (нечетность) функции.
Четная функция – функция, у которой область определения симметрична относительно начала координат и для любого x из области определения выполняется равенство 𝑓(−𝑥) = 𝑓(𝑥). График четной функции симметричен относительно оси ординат.
Нечетная функция – функция, у которой область определения симметрична относительно начала координат и для любого x из области определения справедливо равенство 𝑓(−𝑥) = −𝑓(𝑥). График нечетной функции симметричен относительно начала координат.
Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число 𝑀, что
|𝑓(𝑥)| ≤ 𝑀 для всех значений 𝑥. Если такого числа не существует, то функция – неограниченная
Линейная функция
Теория
Линейная функция — это функция вида 𝑦 = 𝑘𝑥 + 𝑏, где 𝑥 — независимая переменная, 𝑘, 𝑏 — некоторые числа. При этом 𝑘 — угловой коэффициент, 𝑏 — свободный коэффициент.
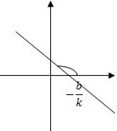
Геометрический смысл коэффициента 𝑏 — длина отрезка, который отсекает прямая по оси 𝑂𝑦, считая от начала координат.
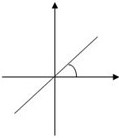
Геометрический смысл коэффициента 𝑘 — угол наклона прямой к положительному направлению оси 𝑂𝑥, считается против часовой стрелки.
Если известно конкретное значение 𝑥, можно вычислить соответствующее значение 𝑦.
Свойства линейной функции:
Область определения линейной функции есть вся вещественная ось;
Если 𝑘 ≠ 0, то область значений линейной функции есть вся вещественная ось. Если 𝑘 = 0, то область значений линейной функции состоит из числа 𝑏;
Четность и нечетность линейной функции зависят от значений коэффициентов 𝑘 и 𝑏.
𝑏 ≠ 0, 𝑘 = 0, следовательно, 𝑦 = 𝑏 – четная;
𝑏 = 0, 𝑘 ≠ 0, следовательно 𝑦 = 𝑘𝑥 –
нечетная;
𝑏 ≠ 0, 𝑘 ≠ 0, следовательно 𝑦 = 𝑘𝑥 + 𝑏 –
функция общего вида;
𝑏 = 0, 𝑘 = 0, следовательно 𝑦 = 0 – как
четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает;
Точки пересечения с осями координат:
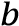
 , следовательно
, следовательно
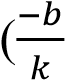 ; 0) – точка пересечения с осью абсцисс.
; 0) – точка пересечения с осью абсцисс.
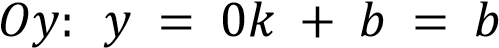 , следовательно
, следовательно 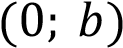 –
–
точка пересечения с осью ординат.
Замечание. Если 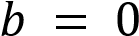 и
и 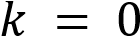 , то
, то 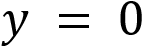 обращается в ноль при любом значении переменной х. Если
обращается в ноль при любом значении переменной х. Если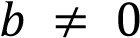 и
и 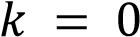 , то функция
, то функция 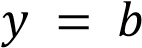 не обращается в ноль ни при каких значениях переменной
не обращается в ноль ни при каких значениях переменной 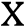 .
.
Промежутки знакопостоянства зависят от коэффициента k.
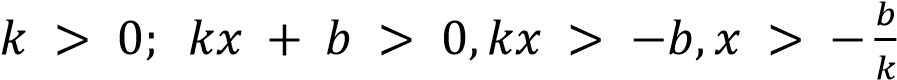 .
.
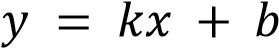 – положительна при
– положительна при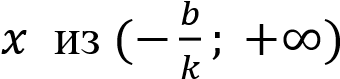 ,
,
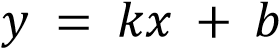 – отрицательна при
– отрицательна при 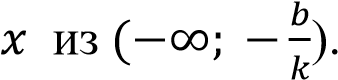
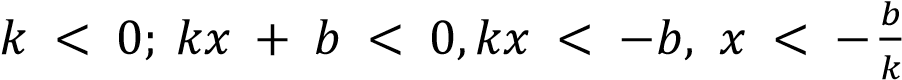 .
.
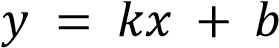 – положительна при
– положительна при  ,
,
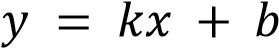 – отрицательна при
– отрицательна при 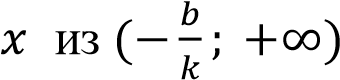 .
.
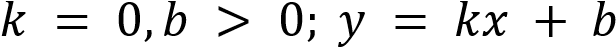 положительна на
положительна на
всей области определения,  отрицательна на всей
отрицательна на всей
области определения.
7) Промежутки монотонности линейной функции зависят от коэффициента  .
.
 , следовательно
, следовательно 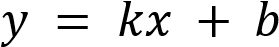 возрастает на
возрастает на
всей области определения,
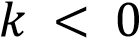 , следовательно
, следовательно убывает на
убывает на
всей области определения.
График линейной функции
Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов 𝑘 и 𝑏. Ниже приведена таблица, которая наглядно это иллюстрирует.
Решение заданий из ОГЭ Задание 1.
На рисунках изображены графики функций вида
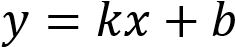 . Установите соответствие между знаками коэффициентов
. Установите соответствие между знаками коэффициентов  и
и  и их графиками функций.
и их графиками функций.
Коэффициенты
А) 
Б) 
В)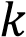

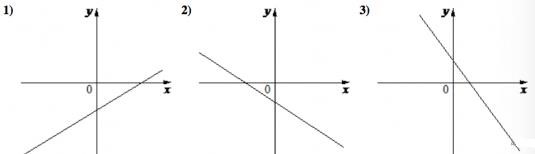
Решение:
Даны три графика функций вида  . Если значение функции возрастает с увеличением
. Если значение функции возрастает с увеличением  , то коэффициент
, то коэффициент  положителен, если убывает – отрицателен. Значение
положителен, если убывает – отрицателен. Значение 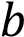 соответствует значению функции в точке
соответствует значению функции в точке 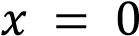 , следовательно, если график пересекает ось ординат выше оси абсцисс, то значение
, следовательно, если график пересекает ось ординат выше оси абсцисс, то значение  положительно, если ниже оси абсцисс – отрицательно.
положительно, если ниже оси абсцисс – отрицательно.
Таким образом, коэффициентам соответствуют следующие графики:
А – 2, Б – 3, В – 1. Ответ: 231.
Задание 2.
На рисунке изображены графики функций вида 𝑦 =
𝑘𝑥 + 𝑏. Установите соответствие между знаками коэффициентов 𝑘 и 𝑏 и графиками.
Коэффициенты
А) 𝑘 , 𝑏 Б) 𝑘 0, 𝑏 0
В) 𝑘 0, 𝑏
Графики

Решение:
Если значение функции возрастает с увеличением x, то коэффициент k положителен, если убывает — отрицателен. Значение b соответствует значению функции в точке x = 0, следовательно, если график пересекает ось ординат выше оси абсцисс, то значение b положительно, если ниже оси абсцисс — отрицательно.
Таким образом, графикам соответствуют следующие коэффициенты: А — 3, Б — 2, В — 1.
Ответ: 321.
Задание 3.
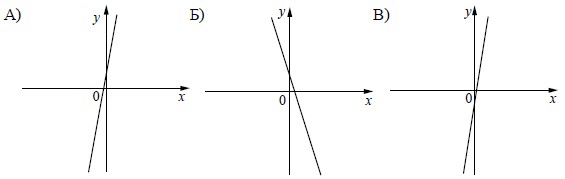
На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
Коэффициенты 1) 𝑘 , 𝑏 0
𝑘 0, 𝑏 0
𝑘 , 𝑏
𝑘 0, 𝑏
Графики
Решение:
Если прямая задана уравнением y=kx + b то при 𝑘 0 функция возрастает, при 𝑘 — убывает. Значению 𝑏 соответствует значение функции в точке 𝑥 = 0 Таким образом, графику A соответствуют коэффициенты 2, Б − 1, В − 4. Ответ: 214
Задание 4.
Установите соответствие между функциями и их графиками.
Функции
А)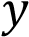
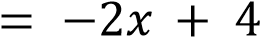
Б) 
В) 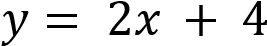
Графики
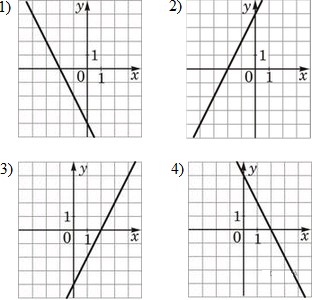
Решение:
Если прямая задана уравнением 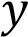
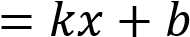 то при
то при  функция возрастает, при
функция возрастает, при 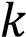
 – убывает. Значению
– убывает. Значению 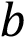 соответствует значение функции в точке
соответствует значение функции в точке 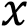
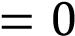
Уравнение 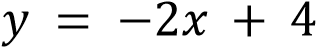 задаёт убывающую функцию, пересекающую ось ординат в точке 4.
задаёт убывающую функцию, пересекающую ось ординат в точке 4.
Уравнение 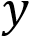
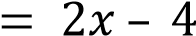 задаёт возрастающую функцию, пересекающую ось ординат в точке −4. Уравнение
задаёт возрастающую функцию, пересекающую ось ординат в точке −4. Уравнение 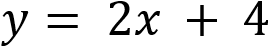 задаёт возрастающую функцию, пересекающую ось ординат в точке 4. Ответ: 432
задаёт возрастающую функцию, пересекающую ось ординат в точке 4. Ответ: 432
Задание 5.
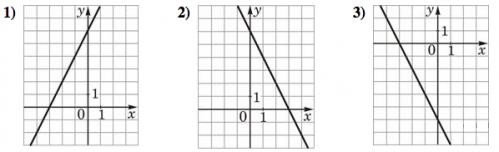
Установите соответствие между функциями и их графиками.
Функции
А) 
Б) 
В)
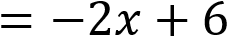
Графики
Решение:
Напомним, что если прямая задана уравнением 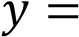
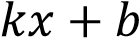 , то: при
, то: при
 тангенс угла наклона прямой к оси абсцисс положителен.
тангенс угла наклона прямой к оси абсцисс положителен.
Уравнение 
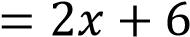 задает прямую, которая пересекает ось ординат в точке 6. Ее график изображен на рисунке 1).
задает прямую, которая пересекает ось ординат в точке 6. Ее график изображен на рисунке 1).
Уравнение 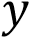
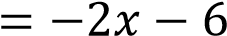 задает прямую, которая пересекает ось ординат в точке -6. Ее график изображен на рисунке 3).
задает прямую, которая пересекает ось ординат в точке -6. Ее график изображен на рисунке 3).
Уравнение 𝑦 = −2𝑥 + 6 задает прямую, которая пересекает ось ординат в точке 6. Ее график изображен на рисунке 2).
Тем самым, искомое соответствие: А — 1, Б — 3, В — 2.
Ответ: 132.
Задание 6.
Постройте график функции 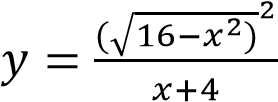 и найдите все значения 𝑎, при которых прямая 𝑦 = 𝑎 имеет с графиком данной функции ровно одну общую точку.
и найдите все значения 𝑎, при которых прямая 𝑦 = 𝑎 имеет с графиком данной функции ровно одну общую точку.
Решение:
Найдём область определения функции:
16 − 𝑥2 ≥ 0;
𝑥𝜖[−4; 4] и 𝑥 + 4 ≠ 0
Значит функция определена при 𝑥 𝜖 (−4; 4].
Поскольку  , получаем что на области определения функция принимает вид 𝑦 = 4 − 𝑥
, получаем что на области определения функция принимает вид 𝑦 = 4 − 𝑥
Теперь строим график
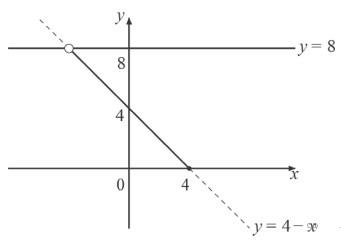
Прямая 𝑦 = 𝑎 имеет с графиком данной функции ровно одну общую точку при 𝑎 𝜖 [0; 8). Ответ: 𝑎 𝜖 [0; 8)
Задание 7
Постройте график функции  и найдите все значения 𝑎, при которых прямая 𝑦 = 𝑎, не имеет с графиком данной функции общих точек.
и найдите все значения 𝑎, при которых прямая 𝑦 = 𝑎, не имеет с графиком данной функции общих точек.
Решение:
Найдем область определения функции:
𝑥2 − 5𝑥 + 6 ≥ 0; 𝑥 𝜖 (−∞; 2] ∪ [3;+∞) и
𝑥 − 3 ≠ 0
Значит, функция определена при:
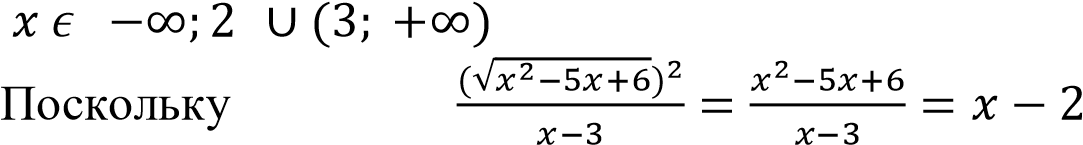 ( ]
( ]
,
получаем, что на области определения функция принимает вид 𝑦 = 𝑥 − 2.
Строим график
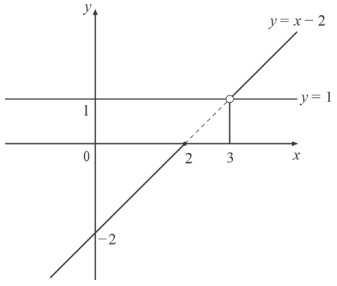
Прямая 𝑦 = 𝑎 не имеет с графиком данной функции общих точек при 𝑎 𝜖 (0,1]
Ответ: 𝑎 𝜖 (0,1]
Задачи для самостоятельного решения
На рисунке изображены графики функций вида
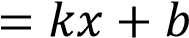 Установите соответствие между графиками функций и знаками коэффициентов
Установите соответствие между графиками функций и знаками коэффициентов  и
и 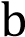 .
.
Коэффициенты
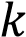
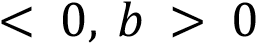
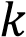
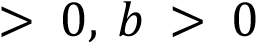
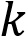
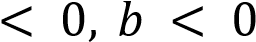
Графики
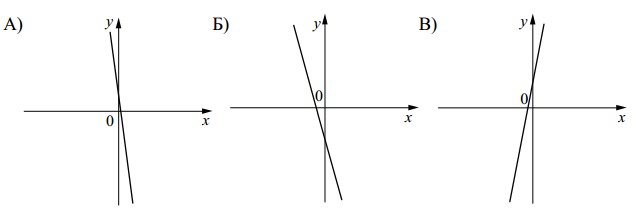
На рисунке изображены графики функций вида 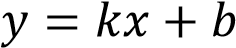 . Установите соответствие между графиками функций и знаками коэффициентов
. Установите соответствие между графиками функций и знаками коэффициентов  и
и .
.
Коэффициенты
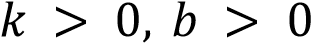
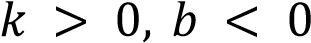

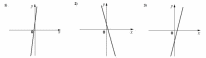
Установите соответствие между функциями и их графиками.
А)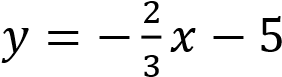
Б)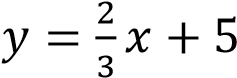
В)
Графики:

Постройте график функции 
 и определите, при каких значениях
и определите, при каких значениях 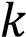 построенный график не будет иметь общих точек с
построенный график не будет иметь общих точек с
прямой 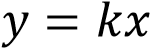
Найдите все значения  , при каждом из которых прямая
, при каждом из которых прямая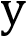
 имеет с графиком функции
имеет с графиком функции
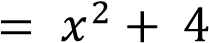 ровно одну общую точку.
ровно одну общую точку.
Постройте этот график и все такие прямые.
Постройте график функции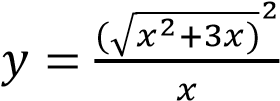 .
.
Найдите значения 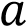 , при которых прямая
, при которых прямая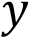
 не имеет с графиком данной функции общих точек.
не имеет с графиком данной функции общих точек.
3.Квадратичная функция
Предполагается, что перед изучением функционально-графического метода решения квадратных уравнений была изучена тема «График функции 𝑦 = 𝑥2».
Основные способы графического решения квадратных уравнений 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0, 𝑎, 𝑏, 𝑐– любые числа, но 𝑎 ≠ 0:
Построить график функции
𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐,
найти точки пересечения с осью абсцисс, которые и будут решением уравнения. Построить два графика 𝑦 = 𝑎𝑥2 и 𝑦 = −𝑏𝑥 − 𝑐, найти абсциссы точек пересечения этих графиков.
Построить два графика
𝑦 = 𝑎𝑥2 + 𝑐 и 𝑦 = −𝑏,
найти абсциссы точек пересечения этих графиков. Графиком первой функции будет парабола, смещенная либо вниз либо вверх, в зависимости от знака числа с. Второй график – прямая, проходящая через начало координат.
Выделить полный квадрат, то есть привести исходное уравнение к виду: 𝑎(𝑥 + 1)2
Построить два графика функции
𝑦 = 𝑎(𝑥 + 1)2 и 𝑦 = −𝑚,
найти их точки пересечения. Графиком первой функции будет парабола, смещенная либо влево, либо вправо, в зависимости от знака числа l.
Графиком второй функции будет прямая, параллельная оси абсцисс и пересекающая ось ординат в точке равной −m.
Разделить исходное уравнение на 
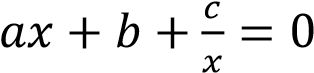 .
.
Преобразовать к виду: 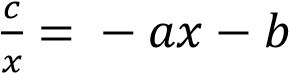 .
.
Решение заданий из ОГЭ
Задание 8
На рисунке изображены графики функций вида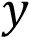
 . Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта
. Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта .
.
Графики
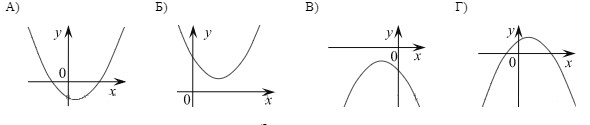
Знаки чисел

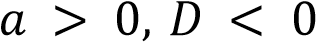
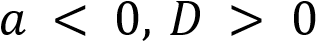
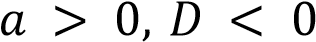
Решение:
График функции
 — парабола. Ветви этой параболы направлены вверх, если
— парабола. Ветви этой параболы направлены вверх, если 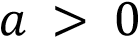 и вниз, если
и вниз, если  .
.
При D 0 уравнение 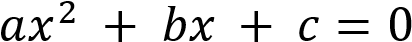 имеет два корня, то есть график функции
имеет два корня, то есть график функции 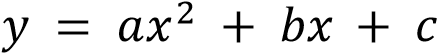 имеет два пересечения с осью
имеет два пересечения с осью
абсцисс. Если  , то корней нет, а соответственно график не пересекает ось абсцисс. Таким образом, получаем ответ: A — 1, Б — 2, В — 4, Г — 3. Ответ: 1243
, то корней нет, а соответственно график не пересекает ось абсцисс. Таким образом, получаем ответ: A — 1, Б — 2, В — 4, Г — 3. Ответ: 1243
Задание 9
На рисунке изображён график квадратичной функции 𝑦 = 𝑓(𝑥).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
𝑓(−1) = 𝑓(3)
Наибольшее значение функции равно 3.
𝑓(𝑥) 0 при −1
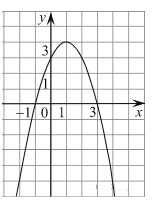
Решение:
Проверим каждое утверждение.
𝑓(−1) = 𝑓(3) Первое утверждение верно.
Наибольшее значение функции равно 4. Второе утверждение неверно.
𝑓(𝑥) 0 при −1 Третье утверждение верно.
Ответ: 2
Задание 10
Найдите значение 𝑐 по графику функции 𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐 изображенному на рисунке.

Решение:
Абсцисса вершины параболы равна 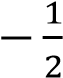 , поэтому
, поэтому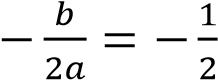 откуда 𝑏 = 𝑎 Парабола пересекает
откуда 𝑏 = 𝑎 Парабола пересекает
ось ординат в точке с ординатой 1, поэтому 𝑐 = 1 Ответ: 1
Задание 11
Постройте график функции
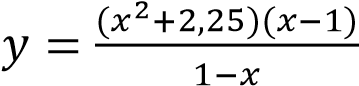
и определите, при каких значениях 𝑘 прямая
𝑦 = 𝑘𝑥
имеет с графиком ровно одну общую точку.
Решение:
Упростим выражение:
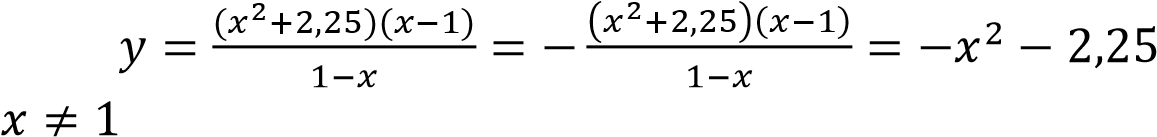 , График исходной функции сводится к графику параболы 𝑦 = −𝑥2 − 2,25 с выколотой точкой (1; -3;25)
, График исходной функции сводится к графику параболы 𝑦 = −𝑥2 − 2,25 с выколотой точкой (1; -3;25)
Построим график функции:
График функции 𝑦 = −𝑥2 − 2,25 получается из графика функции 𝑦 = 𝑥2 отражением относительно оси 𝑂𝑥 и последующим сдвигом на (0; -2,25)

Чтобы прямая 𝑦 = 𝑘𝑥 имела с построенным графиком одну общую точку, нужно чтобы:
или прямая 𝑦 = 𝑘𝑥 была касательной к графику 𝑦 = −𝑥2 − 2,25 (и точка касания не равна 1), или прямая пересекает график в точке и в какой-то
второй точке.
Случай касания реализуется, когда дискриминант квадратного уравнения −𝑥2 − 2,25 = 𝑘𝑥 равен нулю.
𝑘2 − 9 = 0
𝑘 ≠ ±3
Если 𝑘 = −3, точка касания 𝑥 = 1,5, а если 𝑘 = 3, точка касания 𝑥 = −1,5 .
Случай 2. Подставим 𝑥 = 1 в уравнение −𝑥2 − 2,25 = 𝑘𝑥.
получим 𝑘 = −3,25. При этом дискриминант этого уравнения будет больше нуля, значит, еще одно решение точно есть.
Ответ: -3,25; -3,3
Задание 12
Постройте график функции
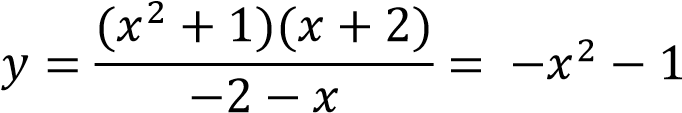
при условии, что 
Решение:
Построим график
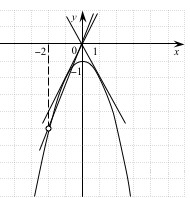
Прямая 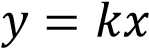 имеет с графиком ровно дну общую точку, если она проходит через точку
имеет с графиком ровно дну общую точку, если она проходит через точку 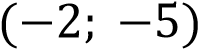 или если уравнение
или если уравнение  имеет один корень. Дискриминант уравнения
имеет один корень. Дискриминант уравнения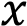
 равен
равен 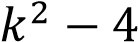 ,
,
и он должен быть равен нулю. Получаем, что 
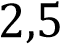 ,
,  и
и
 .
.
Ответ: 2,5; -2; 2.
Задачи для самостоятельного решения
1.Установите соответствие между функциями и их графиками.
Функции
А) 𝑦 = 𝑥2 − 2𝑥 Б) 𝑦 = 𝑥2 + 2𝑥 В) 𝑦 = −𝑥2 − 2𝑥
Графики

2.Установите соответствие между функциями и их графиками.
Функции
А) 𝑦 = 𝑥2 − 2𝑥
Б) 𝑦 = 𝑥2 + 2𝑥
В) 𝑦 = −𝑥2 − 2𝑥
Графики
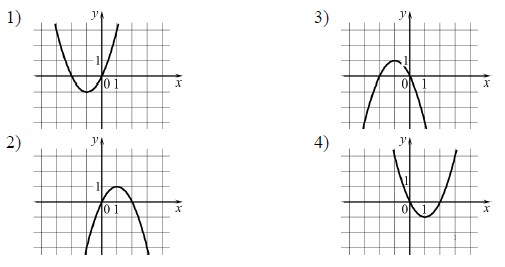
3.На рисунке изображён график функции
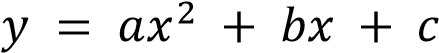 .
.
Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.

Утверждения
А) функция возрастает на промежутке;
Б) функция убывает на промежутке
Помежутки
1) [1;2], 2) [0;2], 3) [-1;0], 4) [-2;3] ОТВЕТ:31
4.Найдите значение  по графику функции
по графику функции
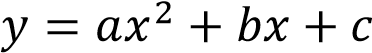 ,
,
изображенному на рисунке
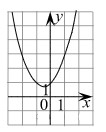
5.Постройте график функции 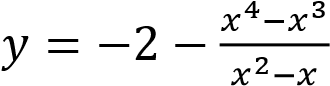 и определите, при каких значениях
и определите, при каких значениях 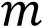 прямая
прямая 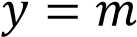 имеет с графиком ровно две общие точки.
имеет с графиком ровно две общие точки.
3.Функция

Графиком функции является гипербола.
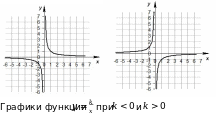
Свойства функции:
Область определения функции:
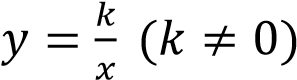 является множество
является множество
всех действительных чисел, кроме 𝑥 = 0,
т.е. 𝐷(𝑦): (−∞, 0) U (0, ∞);
множеством значений функции являются все числа, кроме 𝑦 = 0, т.е. промежуток 𝐸(𝑦): (−∞, 0) U (0, ∞);
наименьшего и наибольшего значений функция 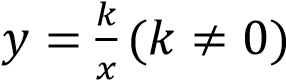 не имеет;
не имеет;
функция является нечетной, график симметричен относительно начала координат (0; 0);
функция непериодическая;
график функции не пересекает координатных
осей;
функция не имеет нулей;
функция  на каждом из промежутков (−∞, 0) и (0, ∞) является убывающей.
на каждом из промежутков (−∞, 0) и (0, ∞) является убывающей.
Функция 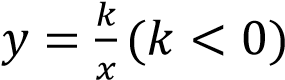 на каждом из промежутков(−∞, 0) и (0, ∞) является возрастающей;
на каждом из промежутков(−∞, 0) и (0, ∞) является возрастающей;
функция  принимает отрицательные значения на промежутке (−∞, 0) и положительные значения на промежутке (0, ∞).
принимает отрицательные значения на промежутке (−∞, 0) и положительные значения на промежутке (0, ∞).
Функция 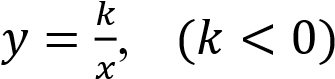 принимает отрицательные значения на промежутке (0, ∞) и положительные значения на промежутке (−∞, 0).
принимает отрицательные значения на промежутке (0, ∞) и положительные значения на промежутке (−∞, 0).
Задание 13
Найдите значение 𝑘 по графику функции 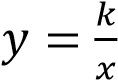 изображенному на рисунке.
изображенному на рисунке.
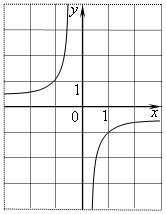
Решение:
Поскольку гипербола проходит через точку
(−1; 1), имеем: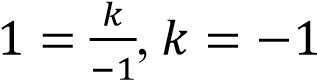
Ответ: -1
Задание 14
График какой из приведенных ниже функций изображен на рисунке?
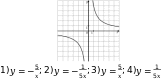
Решение:
Изображённая на рисунке гипербола расположена в первой и третьей четвертях, следовательно, данному графику могут соответствовать функции 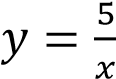 или
или
 . При 𝑥 = 1 ордината функции на графике равна 5, следовательно, это график функции
. При 𝑥 = 1 ордината функции на графике равна 5, следовательно, это график функции 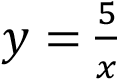
Ответ: 3
Задание 15
Установите соответствие между функциями и их графиками.
Функции:
А) 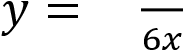 − 1 Б)
− 1 Б) В)
В) 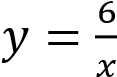
Графики


Решение:
Все представленные здесь функции — гиперболы. Общая формула для уравнения гиперболы:  , если 𝑎 0, то ветви гиперболы располагаются в первой и третьей четвертях, в противном случае — во второй и четвёртой четвертях.
, если 𝑎 0, то ветви гиперболы располагаются в первой и третьей четвертях, в противном случае — во второй и четвёртой четвертях.
Для того, чтобы отличить гиперболы лежащие в одинаковых четвертях нужно подставить какое-нибудь значение 𝑥 в формулу и проверить, какому графику будет соответствовать полученное значение.
Таким образом, установим соответствие: А-4, Б-2, В-1.
Ответ: 421
Задание 16
Постройте график функции  и определите при каких значениях 𝑚 прямая 𝑦 = 𝑚 не имеет с графиком ни одной общей точки. Решение:
и определите при каких значениях 𝑚 прямая 𝑦 = 𝑚 не имеет с графиком ни одной общей точки. Решение:
Преобразуем выражение :  при условии , что 𝑥 ≠ −4.
при условии , что 𝑥 ≠ −4.
Построим график. Прямая 𝑦 = 𝑚 не имеет с графиком ни одной общей точки при 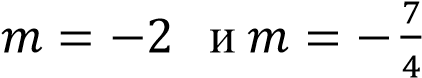

Задание: 17
Постройте график функции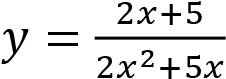 Определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
Определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
Решение:
Упростим выражение для функции:
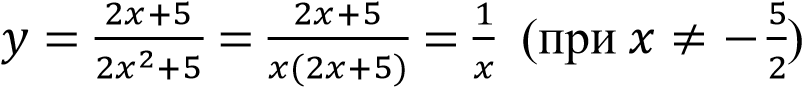
Таким образом, получили, что график нашей функции сводится к графику функции с выколотой
с выколотой
точкой 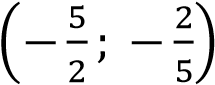
Построим график функции
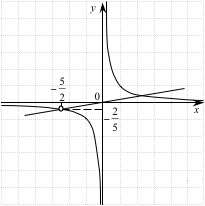
Заметим, что прямая 𝑦 = 𝑘𝑥 проходит через начало координат и будет иметь с графиком функции ровно одну общую точку только тогда, когда будет проходить через выколотую точку 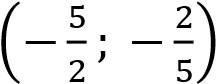 Подставим координаты этой точки в уравнение прямой и найдём коэффициент 𝑘
Подставим координаты этой точки в уравнение прямой и найдём коэффициент 𝑘
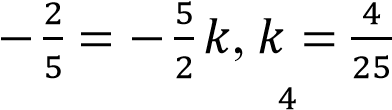
Ответ:
25
Задачи для самостоятельного решения
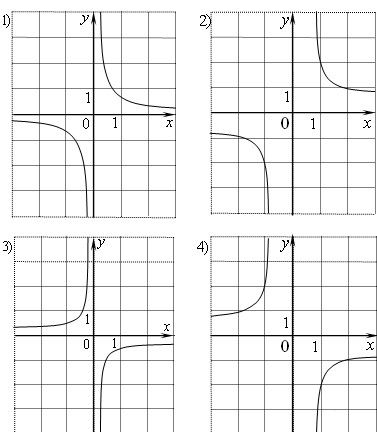
На одном из рисунков изображен график функции
 . Укажите номер этого рисунка
. Укажите номер этого рисунка
Установите соответствие между
функциями и их графиками Функции
А) 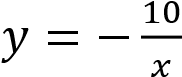
Б)
В)
Графики

На одном из рисунков изображен график
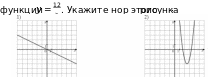

определите, при каких значениях 𝑘 прямая 𝑦 = 𝑘𝑥 имеет с графиком ровно одну общую точку.
5. Постройте график функции  и
и
определите, при каких значениях 𝑘 прямая 𝑦 =
𝑘𝑥 имеет с графиком ровно одну общую точку.
4.Функция
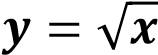

Свойства функции:
выражение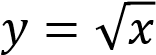 имеет смысл только при неотрицательных значениях 𝑥 ⇒ областью определения функции является промежуток [0; ∞);
имеет смысл только при неотрицательных значениях 𝑥 ⇒ областью определения функции является промежуток [0; ∞);
множеством значений функции является промежуток [0; ∞);
значение функции 𝑦 = 0 является наименьшим, а наибольшего значения функция не имеет;
функция не является ни четной, ни нечетной;
функция непериодическая;
график функции пересекается с осями в
единственной точке – (0; 0);
точка (0; 0) является нулем функции;
функция монотонно возрастает на области определения;
функция принимает положительные значения на промежутке (0; ∞), график расположен в I координатном угле.
Задание 18
Установите соответствие между графиками функций и формулами, которые их задают.
Графики

Функции
1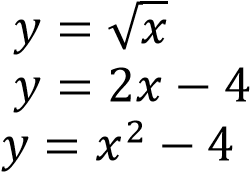 )
)
2)
3)
Решение:
Определим вид графика каждой из функций.
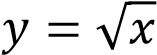 — уравнение верхней ветви параболы, направленной вправо.
— уравнение верхней ветви параболы, направленной вправо.
𝑦 = 2 − 𝑥2 — уравнение параболы с
вертикальным расположением веток,
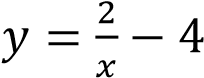 — уравнение прямой.
— уравнение прямой.
Тем самым найдено соответствие: A-1, Б-3, В-2.
Ответ: 132
Задание 19
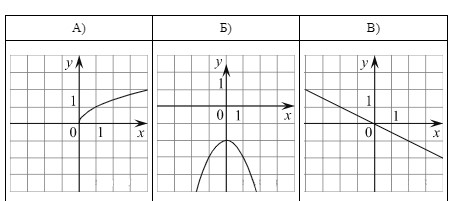
Установите соответствие между графиками функций и формулами, которые их задают.
Графики
Формулы:
1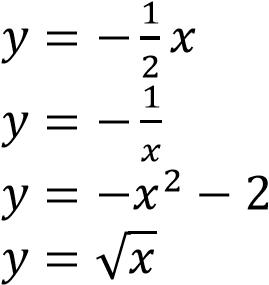 )
)
2)
3)
Решение:
Определим вид графика каждой из функций.
 — уравнение прямой.
— уравнение прямой.
 — уравнение гиперболы.
— уравнение гиперболы.
𝑦 = −𝑥2 − 2 — уравнение параболы, ветви которой направленны вниз.
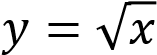 — уравнение верхней ветви параболы, направленной вправо.
— уравнение верхней ветви параболы, направленной вправо.
Ответ: 431.
Задание 20
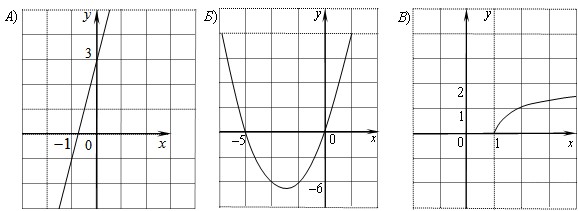
Укажите соответствие между графиками функций и формулами, которые их задают.
Графики
Функции
1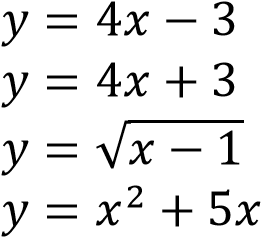 )
)
2)
3)
4)
Решение:
Определим вид графика каждой из функций:
𝑦 = 4𝑥 − 3 уравнение прямой, которая пересекает ось абсцисс в точке 0,75 ; ось ординат в точке
1.
𝑦 = 4𝑥 + 3 уравнение прямой, которая пересекает ось абсцисс в точке −0,75 ; ось ординат в точке 7.
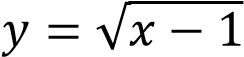 уравнение степенной функции с положительным дробным показателем. В точке 1 значение функции равно 0.
уравнение степенной функции с положительным дробным показателем. В точке 1 значение функции равно 0.
𝑦 = 𝑥2 + 5𝑥 уравнение параболы, которая пересекает ось абсцисс в точках 0 и -5.
Таким образом, искомое соответствие: A-2, Б -4, В-3.
Ответ: 243.
Задание 21
Установите соответствие между графиками функций и формулами, которые их задают.
Графики
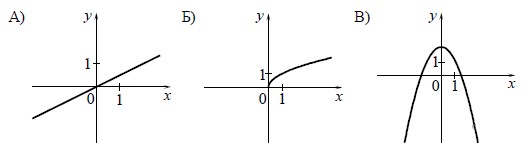
Коэффициенты
1 )
)
2)
3)
4) Решение:
Определим вид графика каждой из функций. 1) – уравнение гиперболы.
– уравнение гиперболы.
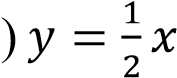 – уравнение прямой.
– уравнение прямой.
) 𝑦 = 2 − 𝑥2 – уравнение параболы.
 – уравнение верхней ветви параболы, направленной вправо.
– уравнение верхней ветви параболы, направленной вправо.
Тем самым найдено соответствие: A–2, Б – 4, В – 3. Ответ: 243.
Задачи для самостоятельного решения
1) Установите соответствие между графиками функций и формулами, которые их задают.
Графики
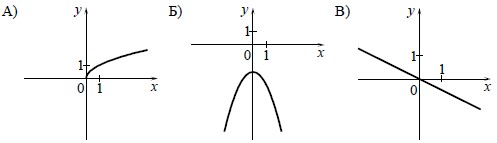
Функции
1 )
)
2)
3)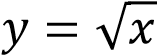
Установите соответствие между графиками функций и формулами, которые их задают
Графики

Функции
1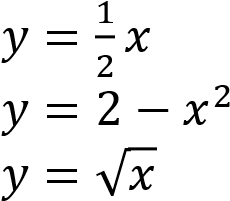 )
)
2)
3)
Найдите наибольшее значение функции
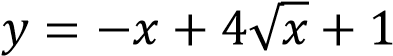 . При каком значении аргумента
. При каком значении аргумента
оно достигается?
5.Функции, содержащие знак модуля
График функции с модулем можно построить стандартным способом и способом преобразования симметрии относительно оси 𝑂𝑥 или оси 𝑂𝑦.
Для построения графиков квадратичных функций, содержащих знак модуля стандартным способом, как и при решении уравнений, сначала находят корни выражений, стоящих под знаком модуля. В результате ось 𝑂𝑥 разбивается на промежутки. Убираем знаки модуля, беря каждое выражение в каждом промежутке с определённым знаком,
которые находим методом интервалов. В каждом промежутке получается функция без знака модуля.
Строим график каждой функции в каждом промежутке.
Для построения графиков функций вида
𝑦 = 𝑎𝑥2 + 𝑏|𝑥| + 𝑐,
𝑦 = |𝑎𝑥2 + 𝑏𝑥 + 𝑐|,
𝑦 = |𝑎𝑥2 + 𝑏|𝑥| + 𝑐| воспользуемся способом симметричного отображения. Рассмотрим это на конкретном примере.
Функция 𝑦 = |𝑥2 − 2𝑥 − 3| Шаг первый:
Строим график функции 𝑦 = 𝑥2 − 2𝑥 − 3. Вершина параболы 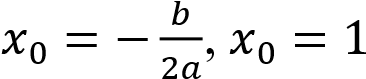 ,
,
𝑦0 = 12 − 2 ∗ 1 − 3 = −4.
Нули функции: 𝑥1 = −1, 𝑥2 = 3
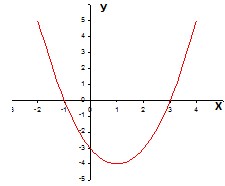
Шаг второй:
Часть графика, которая расположена под осью 𝑂𝑥, симметрично отображаем относительно оси абсцисс.

Шаг третий:
Нижнюю часть графика убираем
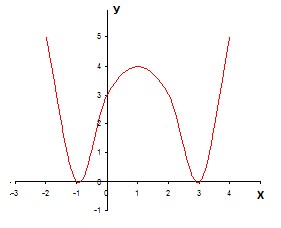
Задание 22
Постройте график функции
𝑦 = 𝑥|𝑥| + 2|𝑥| − 5𝑥
Определите, при каких значениях 𝑚 прямая
𝑦 = 𝑚
имеет с графиком ровно две общие точки.
Решение:
Раскроем модуль.
При 𝑥 ≥ 0 имеем: 𝑦 = 𝑥(𝑥) + 2𝑥 − 5
𝑦 = 𝑥2 − 3𝑥
Графиком данной функции является парабола, ветви которой направлены вверх. Абсцисса вершины: ордината
ордината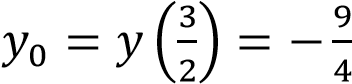 .
.
Точка пересечения графика с осью ординат:
𝑦(0) = 0.
Точки пересечения с осью абсцисс найдем из уравнения 𝑥2 − 3𝑥 = 0, получим: 𝑥 = 0, 𝑥 = 3.
Дополнительная точка: 𝑦(4) = 4.
При 𝑥 имеем:
𝑦 = 𝑥(−𝑥) + 2(−𝑥) − 5𝑥, 𝑦 = −𝑥2 − 7𝑥
Графиком данной функции является парабола, ветви которой направлены вниз.
Абсцисса вершины: 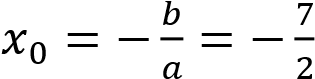 ордината вершины
ордината вершины 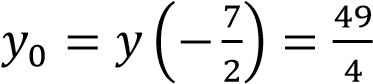 . Точка пересечения графика с осью ординат: 𝑦(0) = 0 Точки пересечения с осью абсцисс найдем из уравнения
. Точка пересечения графика с осью ординат: 𝑦(0) = 0 Точки пересечения с осью абсцисс найдем из уравнения
−𝑥2 − 7𝑥 = 0
получим, 𝑥 = 0, 𝑥 = 7. Дополнительная точка: 𝑦(−8) = −8
Прямая 𝑦 = 𝑚 имеет построенным графиком ровно
две общие точки при 
Ответ: 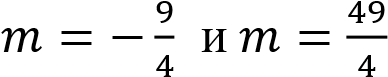
Задание 23
Постройте график функции 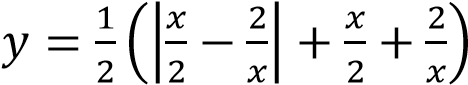 .
.
Определите, при каких значениях 𝑚 прямая 𝑦 = 𝑚 имеет с графиком ровно одну общую точку.
Решение:
Значение выражения 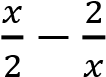 неотрицательно при −2 ≤ 𝑥 и 𝑥 ≥ 2, а при 𝑥 и 0 значение этого выражения отрицательно. Посмотрим график функции
неотрицательно при −2 ≤ 𝑥 и 𝑥 ≥ 2, а при 𝑥 и 0 значение этого выражения отрицательно. Посмотрим график функции 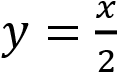 при −2 и 𝑥 ≥ 2 и график функции
при −2 и 𝑥 ≥ 2 и график функции 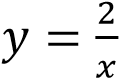 при 𝑥 и 0 . Прямая 𝑦 = 𝑚 имеет с графиком ровно одну общую точку при 𝑚 = 1 и 𝑚 = −1.
при 𝑥 и 0 . Прямая 𝑦 = 𝑚 имеет с графиком ровно одну общую точку при 𝑚 = 1 и 𝑚 = −1.

Задание 24
Постройте график функции 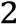 𝑦 = 𝑥 + 11𝑥 − 4|𝑥 + 6| + 30.
𝑦 = 𝑥 + 11𝑥 − 4|𝑥 + 6| + 30.
Определите, при каких значениях 𝑚 прямая
𝑦 = 𝑚
имеет с графиком три общие точки. Решение Имеем:
𝑦 = 𝑥2 + 11𝑥 − 4|𝑥 + 6| + 30;

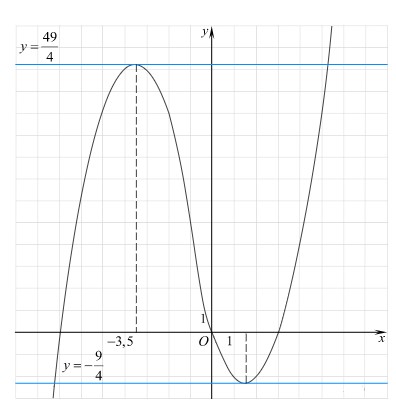
Для построения искомого графика построим график функции 𝑦 = 𝑥2 + 7𝑥 + 6 на промежутке [−6; +∞) и график 𝑦 = 𝑥2 + 15𝑥 + 54 на промежутке (−∞; −6).
Графиком функции 𝑦 = 𝑥2 + 7𝑥 + 6 является парабола, ветви которой направлены вверх, вершина имеет координаты (-3,5; -6,25).
Графиком 𝑥2 + 15𝑥 + 54 является парабола, ветви которой направлены вверх, вершина имеет координаты (-7,5; -2,25). График данной функции изображен на рисунке. Прямая y = m имеет с построенным графиком ровно три общие точки при m = 0 и при m = −2,25.
Ответ: -2,25; 0.
Задание 25
Постройте график функции 𝑦 = |𝑥2 + 3𝑥 + 2|.
Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Решение:
График данной функции — это график параболы 𝑦 = 𝑥2 + 3𝑥 + 2 отрицательная часть которого отражена относительно оси 𝑂𝑥 Этот график изображён на рисунке.
Прямая, параллельная оси абсцисс задаётся формулой 𝑦 = 𝑐, где 𝑐 — постоянная. Из графика видно, что прямая 𝑦 = 𝑐 может иметь с графиком функции не более четырёх общих точек.

Ответ: 4
Задание 26
Постройте график функции 𝑦 = 𝑥2 − 5|𝑥| − 𝑥 и определите, при каких значениях 𝑐 прямая 𝑦 = 𝑐 имеет с графиком ровно три общие точки.
Решение:
Раскрывая модуль, получим, что график функции можно представить следующим образом:

Этот график изображен на рисунке:
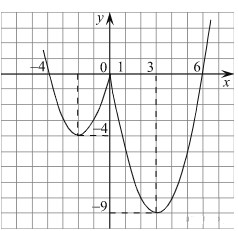
Из графика, видно, что прямая 𝑦 = 𝑐 имеет с графиком функции ровно три общие точки при с = −4, с = 0.
Ответ -4; 0.
Задание 27.
Постройте график функции
 .
.
Определите, при каких значениях 𝑚 прямая
𝑦 = 𝑚
имеет с графиком ровно одну общую точку. Решение:
Раскроем модуль: 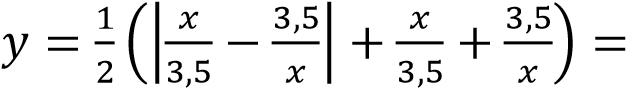

Из графика видно, что прямая 𝑦 = 𝑚 имеет с графиком функции ровно одну общую точку при 𝑚 =
−1 и 𝑚 = 1 Ответ: −1; 1.
Задачи для самостоятельного решения
Постройте график функции
𝑦 = |𝑥 + 1| − |𝑥 − 1|
и найдите все значения 𝑘 при которых прямая
𝑦 = 𝑘𝑥
имеет с графиком данной функции ровно одну
общую точку.
Постройте график функции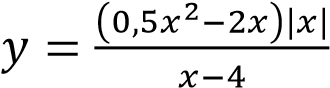 и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.
Постройте график функции и определите, при каких значениях 𝑘 прямая 𝑦 = 𝑘𝑥 не имеет с графиком ни одной общей точки.
и определите, при каких значениях 𝑘 прямая 𝑦 = 𝑘𝑥 не имеет с графиком ни одной общей точки.
Постройте график функции 𝑦 = 𝑥2 − |8𝑥 + 1|. Определите, при каких значениях 𝑚 прямая 𝑦 = 𝑚 имеет с графиком ровно три общие точки.
Постройте график функции 𝑦 = 2𝑥 + 4|𝑥| − 𝑥2 и определите, при каких значениях 𝑐 прямая 𝑦 = 𝑐 имеет с графиком ровно три общие точки.
6.Кусочно-непрерывные функции
Графики кусочно-непрерывных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения. Для того чтобы построить график кусочно-непрерывной функции, необходимо учесть:
При построении графиков кусочно-заданных функций сначала на оси абсцисс найдите граничные точки и разметьте координатную плоскость вертикальными прямыми, проходящим через граничные точки. Назовем получившиеся области полосами.
Строим график в каждой полосе по своей формуле. Если несколько промежутков, на которых формулы разные, то не нужно проводить график каждой из них на всей координатной плоскости.
Помните, что при вычислении значений функции значения 𝑥 нужно выбирать из соответствующих областей определения для каждой формулы. В каждой полосе считаем значения по соответствующей формуле.
Если граничная точка входит в промежуток (например, 𝑦 = 𝑥2 − 20, если 𝑥 ≤ 5), то считаем в ней значение функции (𝑦 = 52 − 20 = 5) и точку (5;5) оставляем «черной». Если граничная точка не входит в промежуток, но граничит с ним (например, 𝑦 = 3𝑥, если 𝑥 5), то считаем в ней значением функции на том участке, в который эта точка входит.
Если в граничной точке значения «граничащих» функции равны, то точку не нужно выделять.
Задание 28
Постройте график функции
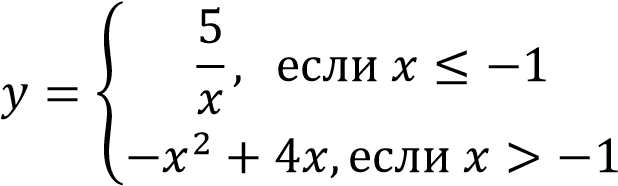
и определите, при каких значениях 𝑦 = 𝑐 будет
пересекать график в трех точках.
Решение:
Выделим полный квадрат
𝑦 = −𝑥2 + 4𝑥 = −𝑥2 + 4𝑥 − 4 + 4 =
= −(𝑥2 − 4𝑥 + 4) + 4 = −(𝑥 − 2)2 + 4
Следовательно, график функции 𝑦 = −𝑥2 + 4𝑥 получаем из графика функции 𝑦 = 𝑥2 сдвигом на (2; 4) и отражением вдоль оси 𝑂𝑥.
График функции  получается из графика функции
получается из графика функции 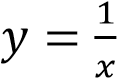 растяжением в 5 раз.
растяжением в 5 раз.
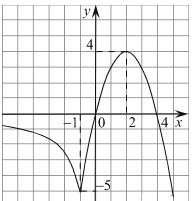
Из графика видно, что прямая 𝑦 = 𝑐 будет иметь с графиком функции ровно три точки пересечения при 𝑐 принадлежащем множеству: (-5; 0) Ответ: (-5; 0).
Задание 29
Построить график функции

Определите, при каких значениях 𝑚 прямая 𝑦 = 𝑚 имеет с графиком ровно две общие точки.
Решение:
Построим график функции 𝑦 = −𝑥 + 3 при 𝑥 и график функции 𝑦 = −𝑥2 + 10𝑥 − 21при 𝑥 ≥ 3.
Прямая 𝑦 = 𝑚 имеет с графиком ровно две общие точки при 𝑚 = 0 и 𝑚 = 4
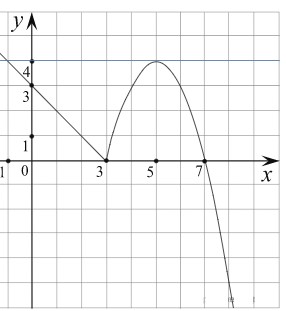
Ответ: при 𝑚 = 0 и 𝑚 = 4
Задание 30
Постройте график функции

Определите, при каких значениях m прямая y = m имеет с графиком ровно одну общую точку.
Решение:
Построим график функции при 𝑥 и график функции 𝑦 = 𝑥2 + 4𝑥 + 5 при 𝑥 ≥ −5.
при 𝑥 и график функции 𝑦 = 𝑥2 + 4𝑥 + 5 при 𝑥 ≥ −5.
Прямая  имеет с графиком ровно одну общую точку при
имеет с графиком ровно одну общую точку при  и при
и при  .
.

Ответ:
Задание 31
Постройте график функции
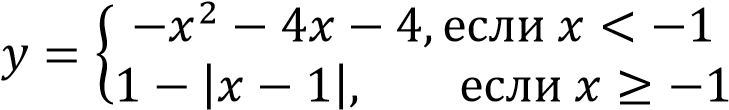
и определите, при каких значениях параметра 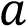 он
он
имеет ровно две общие точки с прямой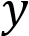
 .
.
Решение:
Преобразуем выражения:

График функции 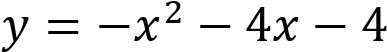 получается из графика функции
получается из графика функции 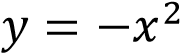 сдвигом на
сдвигом на  и отражением через ось
и отражением через ось 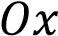 . Построим его на промежутке
. Построим его на промежутке
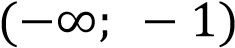 .
.
Построим график функции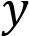
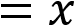 на промежутке
на промежутке 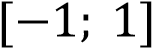 и график функции
и график функции 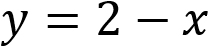 на промежутке
на промежутке

.
Прямая  имеет с построенным графиком ровно две общие точки при
имеет с построенным графиком ровно две общие точки при 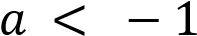 и при
и при 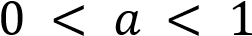 .
.
Ответ:  ,
, 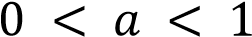 .
.
Задание 32.
Постройте график функции
 и определите, при каких
и определите, при каких
значениях 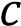 прямая
прямая  будет иметь с графиком единственную общую точку. Решение:
будет иметь с графиком единственную общую точку. Решение:

Из графика видно, что прямая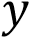
 будет иметь с графиком функции единственную точку пересечения при
будет иметь с графиком функции единственную точку пересечения при принадлежащем множеству
принадлежащем множеству  .
.
Ответ: 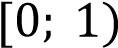 .
.
Задание 33
Постройте график функции
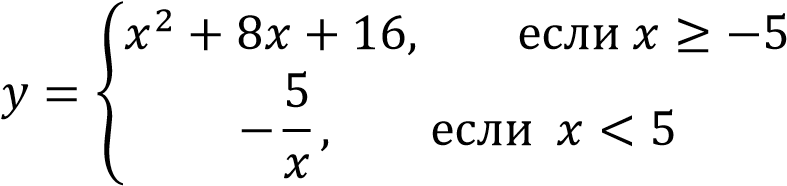
Определите, при каких значения  прямая
прямая
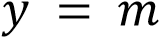
имеет с графиком одну или две общие точки.
Решение:
График функции
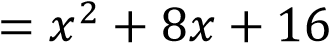 получается из графика функции
получается из графика функции  сдвигом на
сдвигом на  . График функции
. График функции получается из графика функции
получается из графика функции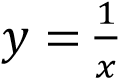 растяжением в 5 раз и отражением через ось
растяжением в 5 раз и отражением через ось 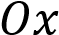 .
.
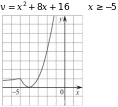
Построим график функции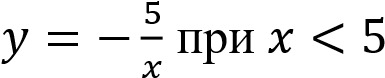 и график функции при
и график функции при
Прямая 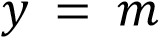 имеет с графиком одну или две общие точки при
имеет с графиком одну или две общие точки при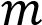
 или при
или при 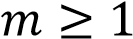 Ответ:
Ответ: 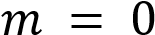 или при
или при 
Задачи для самостоятельного решения
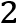 Постройте график функции
Постройте график функции
 и определите, при каких
и определите, при каких
значениях параметра  прямая
прямая
 имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Постройте график функции
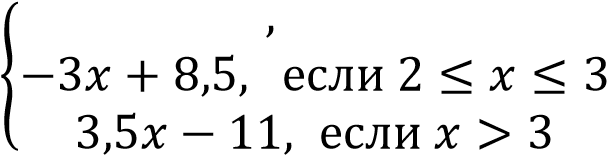
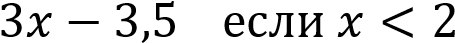 и определите, при каких
и определите, при каких
значениях прямая 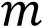 прямая
прямая 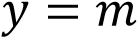 имеет с графиком ровно две общие точки.
имеет с графиком ровно две общие точки.
 Постройте график функции
Постройте график функции
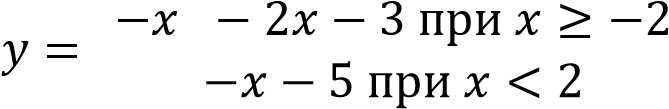
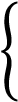
Определите, при каких значениях  прямая
прямая
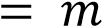 имеет с графиком ровно две общие точки.
имеет с графиком ровно две общие точки.
 Постройте график функции
Постройте график функции
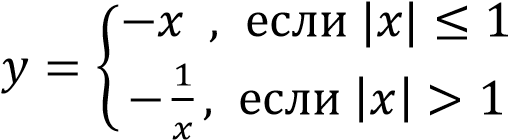 и определите, при каких значениях параметра
и определите, при каких значениях параметра 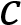 прямая
прямая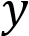
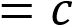 имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
5. Постройте график функции
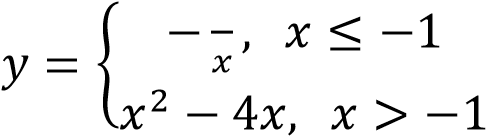
 и определите, при каких
и определите, при каких
значениях 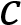 прямая
прямая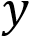
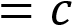 будет пересекать построенный график в трех точках.
будет пересекать построенный график в трех точках.
7.Нахождение наименьшего и наибольшего значения
Число m называют наименьшим значением функции 𝑦 = 𝑓(𝑥) на множестве 𝑋 ⊂ 𝐷(𝑓), если
существует точка 𝑥0 ∈ 𝑋, такая, что 𝑓(𝑥0) = 𝑚;
для любого значения 𝑥 ∈ 𝑋 выполняется неравенство 𝑓(𝑥) ≥ 𝑓(𝑥0).
Число M называют наибольшим значением функции 𝑦 = 𝑓(𝑥) на множестве 𝑋 ⊂ 𝐷(𝑓), если
существует точка 𝑥0 ∈ 𝑋, такая, что 𝑓(𝑥0) = 𝑀;
для любого значения 𝑥 ∈ 𝑋 выполняется неравенство 𝑓(𝑥) ≤ 𝑓(𝑥0).
Если функция имеет наибольшее значение 𝑦наиб, то её называют ограниченой сверху.
Если функция имеет наименьшее значение 𝑦наим, то её называют ограниченной снизу.
Соответственно, можно рассуждать наоборот. Если функция не ограничена сверху, то у неё не существует наибольшего значения 𝑦наиб. И если функция не ограничена снизу, то у неё не существует наименьшего значения 𝑦наим.
Задача 39
Найдите наименьшее значение выражения и
значения 𝑥 и 𝑦, при которых оно достигается
|6𝑥 + 5𝑦 + 7| + |2𝑥 + 3𝑦 + 1|
Решение:
Сумма |6x+5y+7|+|2+3y+1| принимает наименьшее значение, равное 0, только в том случае, когда оба слагаемых одновременно равны 0. Получаем систему уравнений

Далее решаем эту систему:

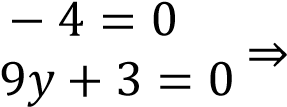
Задача 40
Постройте график функции:  .
.
Найдите наибольшее и значение функции на отрезке

Решение:
По формуле найдем 
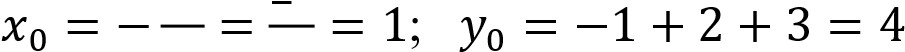

(1;4) – вершина параболы, ветви которой направлены вниз  это и будет наибольшей значение функции.
это и будет наибольшей значение функции.

Задание 41
Найдите наименьшее значение уравнения
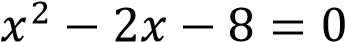 .
.
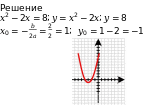
Ответ: (-2; 4)
Задание 42
Найдите наименьшее значение выражения
(5𝑥 − 4𝑦 + 3)2 + (3𝑥 − 𝑦 − 1)2
и значения 𝑥 и 𝑦, при которых оно достигается.
Решение.
При любых значениях 𝑥 и 𝑦 имеем
(5𝑥 − 4𝑦 + 3)2 + (3𝑥 − 𝑦 − 1)2 ≥ 0 .
Значение, равное 0, достигается только в том случае, когда 5𝑥 − 4𝑦 + 3 и 3𝑥 − 𝑦 − 1 равны нулю одновременно. Составим систему уравнений
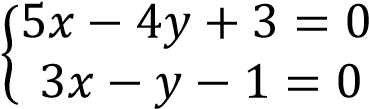
Решив её, получим 𝑥 = 1, 𝑦 = 2
Таким образом, наименьшее значение выражения равно 0, оно достигается при 𝑥 = 1, 𝑦 = 2 Ответ: 0, при 𝑥 = 1, 𝑦 = 2
Задачи для самостоятельного решения. 1. Найдите наименьшее значение выражения
|3𝑥 − 4𝑦 − 2| + |𝑥 − 5𝑦 + 3| и значения 𝑥 и 𝑦, при которых оно достигается.
Найдите наибольшее значение функции
 2
2
Найдите наименьшее значение выражения
(5𝑥 − 4𝑦 + 3)2 + (3𝑥 − 𝑦 − 1)2 и значения 𝑥 и 𝑦, при которых оно достигается.
Найдите наименьшее значение выражения
|6𝑥 + 5𝑦 + 7| + |2𝑥 + 3𝑦 + 1| и значения 𝑥 и 𝑦, при которых оно достигается.
Ответы к практикумам по заданиям из ОГЭ
Линейная функция
132
132
231
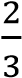 ; 1; 2
; 1; 2
−4; 4
𝑎 𝜖 (0; 3]
Квадратичная функция
413
132
31
𝑎 = 1
(−∞; −3) ∪ (−3; 2)
Функция 
1 .
.
2.
3.
4.
5.

Функция 𝑦 = √𝑥
312
132
-9 при 𝑥 = 9
2 при 𝑥 = 3
Функции, содержащие знак модуля
1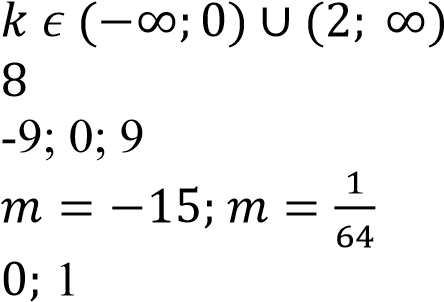 .
.
2.
3.
4.
5.
Кусочно–непрерывные функции
(1; 0]
-0,5; 2,5
𝑚 = −2 и 𝑚 = −3
[0; 1)
(0;5)
Нахождение наименьшего и наибольшего значения
0; (2; 1)
2
0; (1; 2)
0; (-2; 1)
Список литературы
Дремов В.А. Задачи ОГЭ с развернутым ответом. 9-й класс/ В.А. Дремов, А.П. Дремов; под. ред. Ф. Ф. Лысенко, С.Ю.Кулабухова. – 4-е изд., доп.- Ростов н/Д: Легион,2019. – 176с.- (ОГЭ). ISBN 978-5-9966-1323-6
Макарычев Ю.Н. Алгебра. 7 класс: учеб. для обобщеобразоват. учреждений/ А45 [Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова]; под.ред.
С.А.Теляковского. – М.:Просвещение, 2013. – 256 с.: ил. – ISBN 978-5-09-018967-5.
Макарычев Ю.Н. Алгебра. 8 класс: учеб. для обобщеобразоват. учреждений/ А45 [Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова]; под.ред.
С.А.Теляковского. – М.:Просвещение, 2013. – 287 с.: ил. – ISBN 978-5-09-022881-7.
Макарычев Ю.Н. Алгебра. 8 класс: учеб. для обобщеобразоват. учреждений/ А45 [Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова]; под.ред.
С.А.Теляковского. – М.:Просвещение, 2014. – 2871 с.: ил. – ISBN 978-5-09-032009-2.
ФГБНУ «ФИПИ». – Москва. – URL: https://fipi.ru/ (дата обращения: 06.11.2020). – Текст: электронный.
Федеральный государственный образовательный стандарт основного общего образования, утвержден приказом Министерства образования и науки Российской Федерации от 17 декабря 2010 г. №1897. [Электронный ресурс]. Режим доступа: https://fgos.ru/ (дата обращения 27.04.2020).
Электронный ресурс – Решу ОГЭ. URL:
https://oge.sdamgia.ru/ (Дата обращения 15.05.2021)



















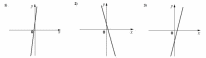







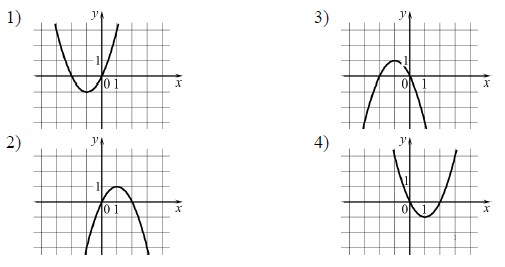




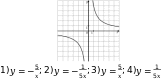










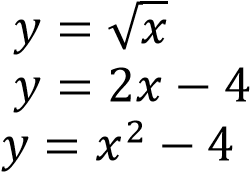 )
)
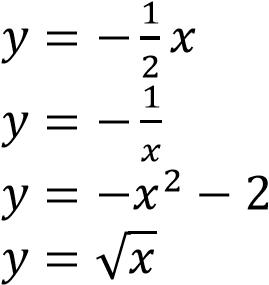 )
)
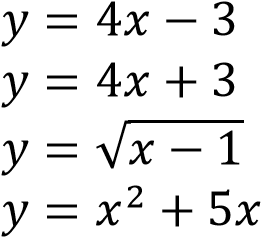 )
)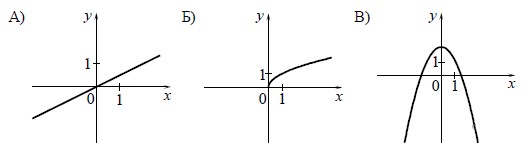
 )
)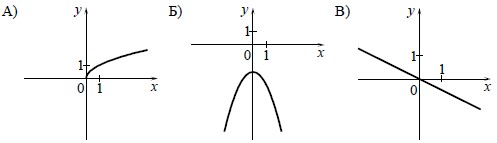

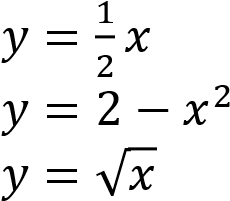 )
)








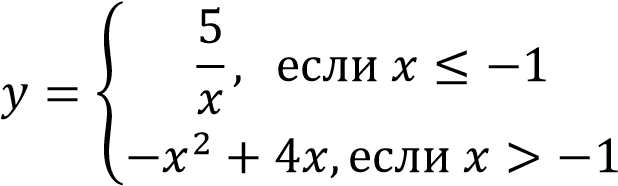







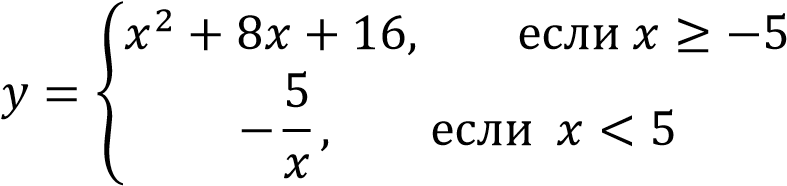

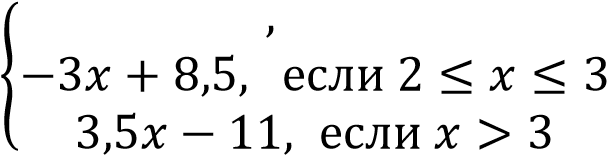



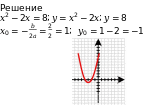

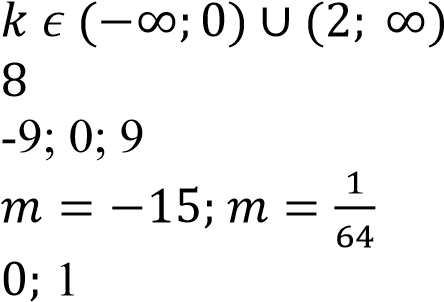 .
. 
















