Преобразование выражений
Теоретический материал
Рациональные выражения
Формулы сокращенного умножения многочленов
(a + b)(a – b) = a2 – b2. | 4. (a + b)(a2 – ab + b2) = a3 + b3. | 7. (a – b)3 = a3 – 3a2b + 3ab2 – b3. |
(a + b)2 = a2 + 2ab + b2. | 5. (a – b)(a2 + ab + b2) = a3 – b3. |
|
(a – b)2 = a2 – 2ab + b2. | 6. (a + b)3 = a3 + 3a2b + 3ab2 + b3. |
|
Формулы корней квадратного уравнения
Алгебраическое уравнение 2-й степени называют квадратным. Общий вид квадратного уравнения с одним неизвестным ax2 + bx + c = 0, где a 0.
Дискриминант: D = b2 – 4ac.
Если D
Если D ≥ 0, то  .
.
2. Если b – четное число, то удобнее представить общую формулу в виде
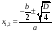 , где
, где  .
.
Формула разложения квадратного трехчлена на множители
ax2 + bx + c = a(x – x1)(x – x2), где x1 , x2 – корни квадратного трехчлена, a ≠ 0.
Теорема Виета
Если приведенное квадратное уравнение x2 + px + q = 0 имеет действительные корни, то 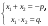
Если квадратное уравнение ax2 + bx + c = 0 (где a ≠ 0) имеет действительные корни, то 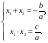
Верны и обратные утверждения.
Основные свойства степени ( x R, y R, a R, a 0, b R, b 0).
а) 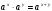 , б)
, б) 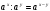 , в)
, в) 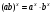 , г)
, г) 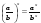 , д)
, д)  , e)
, e)  , ж)
, ж) 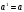 , з)
, з)  .
.
Иррациональные выражения
Определение 1. Корнем n-й степени из неотрицательного числа a (n = 2, 3, 4, 5, …) называют такое неотрицательное число, которое при возведении в степень n дает в результате число a.
Определение 2. Корнем нечетной степени n из отрицательного числа a (n = 3, 5,7, …) называют такое отрицательное число, которое при возведении в степень n дает в результате число a.
Определение 3. Если 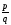 – обыкновенная дробь (
– обыкновенная дробь (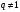 ) и
) и  , то под
, то под  понимают
понимают 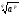 , т.е.
, т.е.  .
.
Свойства функции  при четной степени n (n = 2, 4, 6, …):
при четной степени n (n = 2, 4, 6, …):
1) 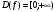 ;
;
2) функция не является ни четной, ни нечетной;
3) функция возрастает на 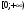 ;
;
4) функция не ограничена сверху, ограничена снизу;
5) функция не имеет наибольшего значения; yнаим= 0;
6) функция непрерывна;
7) 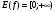 .
.
Свойства функции 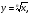 при нечетной степени n (n = 3, 5, 7, …):
при нечетной степени n (n = 3, 5, 7, …):
1)  ;
;
2) функция нечетна;
3) функция возрастает;
4) функция не ограничена ни сверху, ни снизу;
5) функция не имеет наибольшего и наименьшего значений;
6) функция непрерывна;
7)  .
.
Свойства корня n-й степени (n = 2, 3, 4, 5, …) из неотрицательного числа ( )
)
1)  ; 2)
; 2)  (
( ); 3)
); 3)  ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  .
.
Замечания.  , где
, где  (в частности
(в частности  ).
).  , где
, где  ,
,  .
.
Теорема. При натуральном n уравнение  равносильно системе
равносильно системе 
Логарифмы
Определение. Логарифм числа х по основанию а есть показатель степени, в которую надо возвести число а, чтобы получить х.
Тождество  (где x 0, a 0 и a 1) называют основным логарифмическим тождеством.
(где x 0, a 0 и a 1) называют основным логарифмическим тождеством.
Определение. Логарифмической функцией называется функция вида у = log x, где a 0, a 1.
x, где a 0, a 1.
Основные свойства логарифмической функции у = log x (a 0, a 1).
x (a 0, a 1).
1. D(loga ) = R+ .
2. E(loga ) =R.
3. Логарифмическая функция на всей области определения возрастает при а 1 и убывает при 0 a
4. Основные свойства логарифмов.
4.1. При любых a 0 (a 1), b 0 (b 1), x 0, y 0, p R, k R верны равенства:
| а)  ; ; б)  ; ; в)  ; ; г)  | д)  ; ; e)  ; ; ж)  (в частности (в частности  ). ). |
| 4.2. При любых a 0 (a 1), b 0 (b 1), x ≠ 0, y ≠ 0, p N верны равенства: а)  ; б) ; б)  в)  . . |
При решении логарифмических уравнений и неравенств используются теоремы, вытекающие из свойств монотонности логарифмической функции.
Теорема 1. Если  , то
, то
log f(x) = log
f(x) = log g(x)
g(x)
Теорема 2. log (f(x)) = b f(x)= a
(f(x)) = b f(x)= a (a 0, a 1).
(a 0, a 1).
Теорема 3. Если a 1, то
log f(x) log
f(x) log g(x)
g(x)
Теорема 4. Если 0 a
log f(x) log
f(x) log g(x)
g(x)
1. ОГЭ, 1_31412. Найдите значение выражения  . Ответ: −2.
. Ответ: −2.
2. ОГЭ, 1_337273. Найдите значение выражения  . Ответ: 0,8.
. Ответ: 0,8.
3. ОГЭ, 1_287946. Найдите значение выражения  . Ответ: 12,5.
. Ответ: 12,5.
4. ОГЭ, 21_311255. Упростите выражение  . Ответ: 0,5.
. Ответ: 0,5.
5. ОГЭ, 21_311552. Один из корней уравнения 5x2 – 2x + 3p = 0 равен 1. Найдите второй корень. Ответ: − 0,6.
6. Найдите  , если
, если  , при
, при  .
.
7. Найдите  , если
, если  .
.
8. Найдите  , если
, если  при
при  .
.
9. Найдите  , если
, если  .
.
10. Найдите  при
при  .
.
11. Найдите  , если
, если  .
.
12. Найдите значение выражения  .
.
13. Найдите значение выражения  .
.
14. Найдите значение выражения  при b = 6.
при b = 6.
15. Найдите значение выражения  при x = 3.
при x = 3.
16. Найдите значение выражения  .
.
17. Найдите корень уравнения:  . Если уравнение имеет более одного корня, укажите меньший из них.
. Если уравнение имеет более одного корня, укажите меньший из них.
18. Найдите значение выражения  .
.
19. Найдите значение выражения  .
.
20. Найдите значение выражения  .
.
21. Вычислите значение выражения:  .
.
22. Решите уравнение  .
.
23. Решите уравнение  .
.
24. Решите уравнение  .
.
25. Решите уравнение  . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
26. Найдите ошибку
|  . О.Д.З.: . О.Д.З.:  . .
|
| 




x = – 1 c учетом О.Д.З. корней нет. Ответ: корней нет. | 




 c учетом О.Д.З. c учетом О.Д.З. 
Ответ:  . . |
27. Решите уравнение . Ответ: 625.
Критерии оценивания задания 21 ОГЭ







 .
.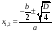 , где
, где  .
.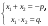
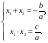
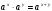 , б)
, б) 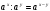 , в)
, в) 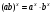 , г)
, г) 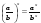 , д)
, д)  , e)
, e)  , ж)
, ж) 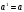 , з)
, з)  .
. 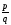 – обыкновенная дробь (
– обыкновенная дробь (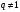 ) и
) и  , то под
, то под  понимают
понимают 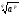 , т.е.
, т.е.  .
. при четной степени n (n = 2, 4, 6, …):
при четной степени n (n = 2, 4, 6, …):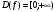 ;
;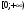 ;
;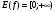 .
.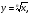 при нечетной степени n (n = 3, 5, 7, …):
при нечетной степени n (n = 3, 5, 7, …): ;
;
















