Содержание и методика преподавания сложных тем учебной программы предмета в процессе подготовки учащихся к ЕНТ.
Целями Единого Национального тестирования являются организация единого государственного контроля качества общего образования на заключительном этапе и обеспечение всем желающим равного доступа к высшему образованию. Что такое для нас ЕНТ? Во-первых - это внешняя экспертиза по единым правилам. Во-вторых - это и способ создать определенные тенденции в развитии системы образования. В-третьих - это способ управлять качеством системы и введение элементов конкуренции в систему образования. В-четвертых - это способ анализа эффективности работы системы.
Умение правильно отвечать на вопросы тестовых заданий, выбирать правильный вариант ответа - обычный навык, которым можно овладеть. Для этого нужно организовать не только работу на уроках, но и дополнительные занятия. В любом случае положительный эффект от таких занятий будет только в том случае, если они носят систематический и планомерный характер. Целью этих занятий является не «натаскивание» на угадывание ответов, а обучение методам, алгоритмам, приемам работы с тестовыми заданиями.
Учитель должен знать виды и типы тестов, формы предтестовых заданий, различные методы оценивания результатов тестирования, уметь анализировать полученные данные в рамках классической и современной теории создания тестов и их использованию в педагогической практике. Нужно готовить учащихся к новой форме проведения экзамена. Использование на уроках тренировочных тестов поможет учащемуся выработать умения обращения с ними. Знание типовых конструкций тестовых заданий поможет учащимся практически не тратить время на понимание конструкции, а также на то, чтобы успокоиться. Такие тренировки выполнения тестовых заданий научат школьников мобилизовать себя в решающей ситуации.
Анализ выполнения учащимися тестов, показал, что наибольшее число ошибок при выполнении заданий ЕНТ по физике учащиеся допускают при решении задач по разделу механика, в который входят кинематика, динамика, законы сохранения.
Одним из методов преподавания сложных тем по физике является алгоритмический метод.
Под алгоритмом подразумевается некий определённый для данного круга задач порядок выполнения операций. Это совокупность точных правил и закономерностей, показывающих, как нужно распорядиться своим знанием, чтобы получить решение или достичь цели. Как учил академик А.Ершов, «алгоритм позволяет не угадывать решение или находить его от случая к случаю, а приходить к нему закономерно, следуя точным правилам».
Ведь если вдуматься, то вся наша жизнь алгоритмизирована: значительную часть того, что мы совершаем, мы делаем по алгоритмам – правилам, которые даются нам обучением, воспитанием или нашим жизненным опытом. Чётко сформулированный алгоритм не создаёт какой-либо «неопределённости» в наших действиях: одно действие строго следует за другим, – в этом точность алгоритма.
Решение задач – одно из средств развития мышления. Как показывает опыт, именно неумение решать задачи, незнание методов подхода к их решению создаёт у ученика отрицательное отношение к физике, а потеря интереса порождает неуверенность в собственных силах. Приступая к решению, ученик испытывает трудности с выбором определённого плана решения – ему нужна конкретизация имеющихся знаний. Это заставляет ученика думать. По каждому типу задач в условии могут быть предложены различные физические ситуации. Но алгоритмическое предписание указывает, ЧТО надо делать, а вот КАК делать – ученик решает сам.
Таким образом, изучение и использование алгоритмических методов позволяет создать базу, фундамент, вырабатывает навыки и умения решать типовые, стандартные задачи, а это есть шаг на пути к решению творческих задач.
Вместе с тем каждый учитель должен ясно осознавать, что излишнее увлечение алгоритмизацией может дать «обратный» эффект – выработать стереотип мышления, шаблон, лишить человека самостоятельности, творчества. Поэтому предлагаемый метод нужно рассматривать как один из методов в общем комплексе привития навыков решения задач по физике...
Если частные алгоритмы, рассчитанные на знание фактического материала (подобные клубку Ариадны, указывающему Тесею путь из лабиринта), основаны на точном соблюдении «правил игры», то более высокий уровень мыслительной деятельности формируется с помощью задач, в которых на поставленный вопрос даётся набор ответов, среди которых верен только один. Ученик перестаёт быть «ведомым», а становится активным участником выбора правильного ответа: теперь требуется не только знать и выполнять, но и уметь сопоставлять, обобщать, самостоятельно находить верный путь! Всё это приучает ученика осмысленно относиться к выполнению заданий, вырабатывает у него культуру выполнения любой (!) работы, умение разумно и рационально расходовать своё время.
Для овладения методом решения кинематических задач учащиеся должны усвоить следующее: что такое система отсчёта, скорость, ускорение, путь и перемещение; понять содержание уравнений зависимости координаты и скорости от времени при равномерном и равноускоренном движении; усвоить классический закон сложения скоростей; понять смысл относительности движения и описание движений в различных системах отсчёта.
Много трудностей возникает при попытке наиболее рационально выбрать систему (уровень) отсчёта. В кинематике нет ограничений в том, с каким телом связать систему отсчёта, что принимать за начало координат (точку отсчёта), за начало отсчёта времени. И всё же систему отсчёта следует выбирать таким образом, чтобы движение в ней описывалось наиболее простым способом, чтобы легко определялись начальные условия.
Рассмотрим алгоритмические предписания для довольно большого и разнообразного круга задач на движение тел по вертикали, ибо, как показывает опыт, именно здесь возникают трудности при нахождении кинематических характеристик (так, например, чтобы узнать, где будет находиться брошенное вертикально вверх тело через определённое время, ученики начинают вычислять путь, который тело пройдёт до точки наивысшего подъёма, а затем – вычислять путь, пройденный при падении из высшей точки, и т.д.).
С чего начинать решение задач? По этому поводу весьма иронично высказался венгерский педагог и популяризатор науки Дьердь Пойа: «Прежде чем решать задачу, имеет смысл ознакомиться с её условием». К сожалению, довольно часто учащиеся, бегло просмотрев условие задачи, не вдумываясь в её содержание, начинают решать «свою» задачу, и только потратив впустую уйму времени, начинают понимать допущенную по невнимательности ошибку.
Итак, составим алгоритм:
1. Внимательно ознакомиться с условием задачи и кратко записать данные (при этом разумно начать с записи искомой величины, что позволит потом дописывать дополнительные данные, различные константы), сведя их к единой системе единиц.
2. Проанализировать условие.
3. Выбрать систему отсчёта (тело отсчёта, начало системы координат, начало отсчёта времени, задать направление оси или осей).
4. Расставить в системе отсчёта векторы кинематических характеристик.
5. Установить вид движения вдоль каждой оси и написать кинематические уравнения движения (координаты и скорости) в векторной форме для тела, а если тел несколько, то для каждого.
6. Спроецировать векторы на выбранную ось или оси и записать уравнения движения вдоль каждой оси с учётом знаков проекций векторов на эти оси – в скалярной форме, а также с учётом начальных условий.
7. Решить уравнение относительно искомой величины в общем виде.
8. Подставить в полученную формулу числовые значения входящих в неё величин и вычислить результат.
9. Пользуясь общей формулой, проверить наименование искомой величины, подставив в неё наименования входящих величин.
10. Проанализировать полученный результат, а если это возможно, то оценить его реальность, дав небольшой комментарий.
С сожалением можно отметить, что большое число учеников начинают решение задач с того, что пишут все известные им формулы по данной теме, а потом «подбирают» формулы под данные величины, ничуть не вдумываясь в физическую сущность задачи.
Пример 1. Из некоторой точки вертикально вверх брошен камень с начальной скоростью 10 м/с относительно Земли. Пренебрегая сопротивлением среды, установите, где будет камень через 3 с от начала движения и какой будет его скорость?
Решая задачу, следуем вышеописанному алгоритму:
1. y – ?  – ?
– ?
_____________
 0 = 10 м/с,
0 = 10 м/с,
t = 3 с,
g = 9,8 м/с2.
2. Камень – материальная точка. Движение происходит на высоте, которая много меньше радиуса Земли  g = const.
g = const.
3. СО – Земля. Начало отсчёта – точка бросания. Отсчёт времени ведётся с момента бросания.
5. Движение – равноускоренное, следовательно:
а) уравнение перемещения:
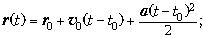
б) уравнение скорости:  (t) =
(t) =  0 + a(t – t0); a = g.
0 + a(t – t0); a = g.
6. Для выбранной оси:
а) y(t) = y0 +  0y(t – t0) +
0y(t – t0) + 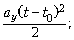
б)  y(t) =
y(t) =  0y + ay(t – t0).
0y + ay(t – t0).
7. Начальные условия: y0 = 0; t0 = 0; ay = –g;  0y =
0y =  0. Отсюда:
0. Отсюда:
а) y(t) =  0t –
0t – 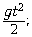
б)  y(t) =
y(t) =  0 – gt.
0 – gt.
8. Ввиду того, что в данной задаче не потребуются какие-либо дополнительные соотношения и нет необходимости преобразовывать уравнения для получения общей формулы, приступаем к подстановке численных значений:
а) y(t) = 10 • 3 –  = –14,1 (м);
= –14,1 (м);
б) б)  y = 10 – 9,8 • 3 = –19,4 (м/с).
y = 10 – 9,8 • 3 = –19,4 (м/с).
9. Проверяем наименования полученных величин:
а) [y] = 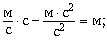
б) [ ] =
] = 
10. Анализ результатов:
Знак «–» у координаты указывает на то, что спустя 3 с от начала движения камень окажется на 14,1 м ниже уровня бросания (разумеется, если точка бросания поднята над Землёй не менее, чем на 14,1 м).
Знак «–» у проекции скорости означает, что в этот момент скорость направлена против выбранной оси (т.е. тело будет «на спуске»).
Кстати, полезно заметить, что алгоритм – это не «жёсткая», а «гибкая» схема, когда требуется выполнение не всех алгоритмических предписаний!
Пример 2. Электромагнит подъёмного крана поднимает кусок железа вертикально со скоростью 10 м/с. В 6 м от Земли этот кусок отрывается. Через какое время после момента отрыва и с какой скоростью он упадёт на Землю? Сопротивлением среды пренебречь.
1. t – ?  – ?
– ?
 0 = 10 м/с,
0 = 10 м/с,
h = 6 м,
g = 10 м/с2.
2. Кусок железа – материальная точка. Ускорение свободного падения постоянно. Движение – прямолинейное.
3. СО – Земля. Начало отсчёта – начальная точка подъёма железа. Начало отсчёта времени – момент отрыва железа от электромагнита.
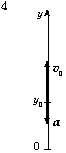
5. r(t) = r0 +  0(t – t0) +
0(t – t0) + 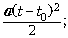
 (t) =
(t) =  0 + a(t – t0);
0 + a(t – t0);
a = g.
6. Скалярные уравнения:
y(t) = y0 +  0y(t – t0) +
0y(t – t0) + 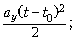
 y(t) =
y(t) =  0y + ay(t – t0).
0y + ay(t – t0).
7. Начальные условия: y0 = h; t0 = 0; ay = –g;  0y =
0y =  0. Дополнительные условия: в момент падения на Землю y(t) = 0. С учётом начальных и дополнительных условий:
0. Дополнительные условия: в момент падения на Землю y(t) = 0. С учётом начальных и дополнительных условий:
y(t) = h +  0t –
0t –  ;
;
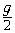 • t2 –
• t2 –  0 • t – h = 0;
0 • t – h = 0;
 y =
y =  0 – gt.
0 – gt.
8. Решив квадратное уравнение относительно времени, подставляем результат в выражение для скорости:
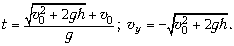
9. Вычисления: t = 2,5 с;  y = –15 м/с.
y = –15 м/с.
10. Позволим себе не проверять в этой задаче наименования.
11. Знак «–» у проекции скорости вполне соответствует тому, что кусок железа падает на Землю, т.е. против выбранной оси.
Пример 3. С Земли вертикально вверх брошено тело со скоростью 100 м/с. Одновременно с ним из точки, находящейся на высоте 100 м над Землёй, по той же вертикали брошено вверх второе тело со скоростью 20 м/с. Где и с какими скоростями столкнутся тела? Сопротивлением среды пренебречь.
1. y – ?  1 – ?
1 – ?  2 – ?
2 – ?
 01 = 100 м/с,
01 = 100 м/с,
h = 100 м,
 02 = 20 м/с,
02 = 20 м/с,
g = 10 м/с.
2. Тела – материальные точки. Движения прямолинейные и равноускоренные. Пренебрегаем зависимостью ускорения свободного падения от высоты над Землёй.
3. СО – Земля. Начало отсчёта – точка бросания тела 1, начало отсчёта времени – момент его броска.

5. Уравнения движения:
r(t) = r0 +  0(t – t0) +
0(t – t0) + 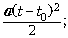
 (t) =
(t) =  0 + a(t – t0);
0 + a(t – t0);
a = g.
6. Проецирование уравнений на оси для обоих тел:
y1 = y01 +  01y(t – t0) +
01y(t – t0) +  ;
;
y2 = y02 +  02y (t – t0) +
02y (t – t0) +  ;
;
 1y =
1y =  01y + ayt;
01y + ayt;  2y =
2y =  02y + ayt.
02y + ayt.
7. Начальные условия: y01 = 0; y02 = h; ay = –g; t0 = 0. Дополнительные условия: при столкновении y1 = y2. Записываем: 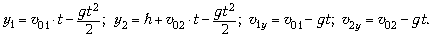
8. Решение в общем виде: 
9. Вычисления: y = 117 м;  1y = 87,5 м/с;
1y = 87,5 м/с;  2y = 7,5 м/с.
2y = 7,5 м/с.
10. По знаку проекций скоростей устанавливаем, что столкновение произойдёт, когда оба тела будут на подъёме.
Навыки, приобретённые при использовании алгоритмических предписаний, позволяют успешно справляться с решением довольно обширного круга задач, формально не подпадающих под разобранные выше предписания. Но отработанное на их применении умение анализировать процесс или явление, «разложить всё по полочкам», расположить информацию в логическом порядке даёт и в этих случаях ощутимые положительные результаты.