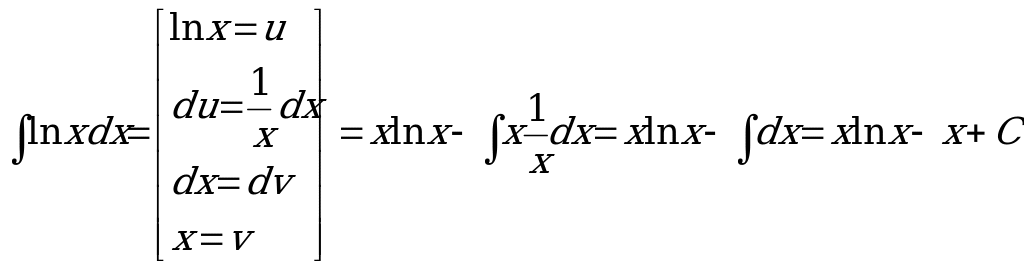5
Лекция№2
Тема: Первообразная функции и неопределенный интеграл.
План:
Первообразная функция.
Неопределенный интеграл и его свойства.
Таблица неопреленных интегралов.
Методы интегрирования.
1. Первообразная функция:
Под дифференцированием функции мы понимаем процесс нахождения производной, но в практике есть еще и обратные задачи, нахождение функции, зная её производную. Процесс нахождения производной и первообразной являются взаимообратные операции.
Определение: Функция F(x) называется первообразной функцией для функции f(x) на интервале (а, b), если F(x) дифференцируема на (а, b) и F'(x) = f(x)
Первообразная обозначается F(x)
Пример: Функция х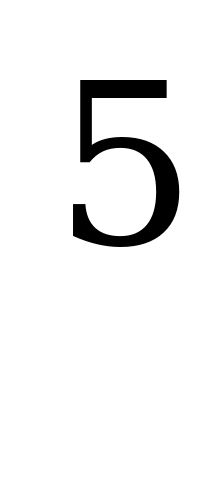 является первообразной для 5х
является первообразной для 5х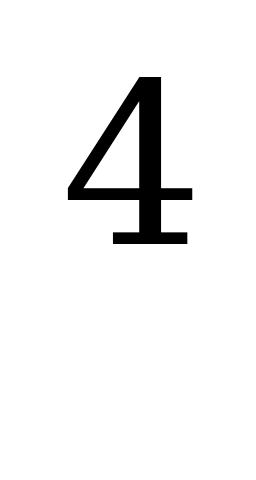 на (-∞;+∞), так как (х
на (-∞;+∞), так как (х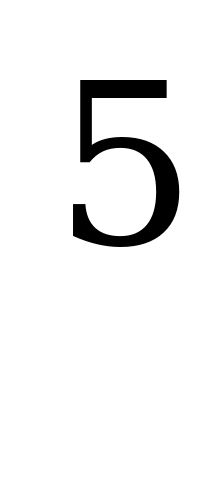 )
)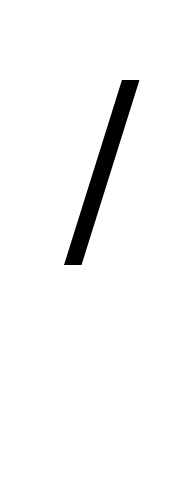 =5х
=5х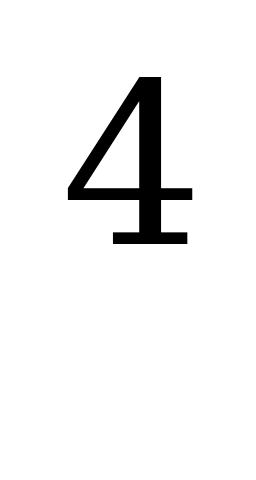
Теорема 1: Если функция непрерывна на каком-нибудь промежутке, то она имеет на нем первообразную. (Без доказательства).
Теорема 2: Если F(x)- первообразная для функции f(x) на интервале (а, b), то F(x) +С, также первообразная , где С - любое число.
Теорема 3:Если F (x) и F
(x) и F (x) – две первообразные для функции f(x) на интервале (а, b), то они на этом промежутке отличаются на постоянную т.е. F
(x) – две первообразные для функции f(x) на интервале (а, b), то они на этом промежутке отличаются на постоянную т.е. F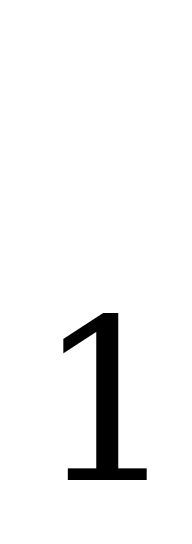 (x) - F
(x) - F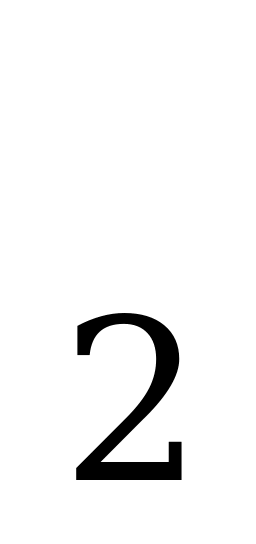 (x) = С
(x) = С
Из данных теорем следует что, если функция f(x) непрерывна на промежутке (а, b), то она имеет не одну первообразную, а множество первообразных.
Множество всех первообразных обозначается F(x) +С
2.Неопределенный интеграл и его свойства.
Действие нахождения первообразной называется интегрированием
Определение: Множество всех первообразных функции f(x) на интервале (а, b) называется неопределенным интегралом от функции f(x) и обозначается символом: 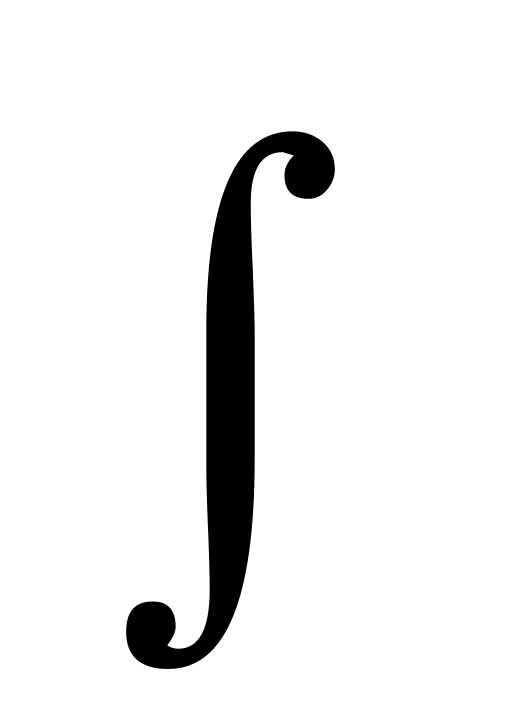 f(x)dx.
f(x)dx.

Где f(x) – подынтегральная функция, dx- дифференциал независимой переменной, f(x)dx – подынтегральное выражение.
Примеры: 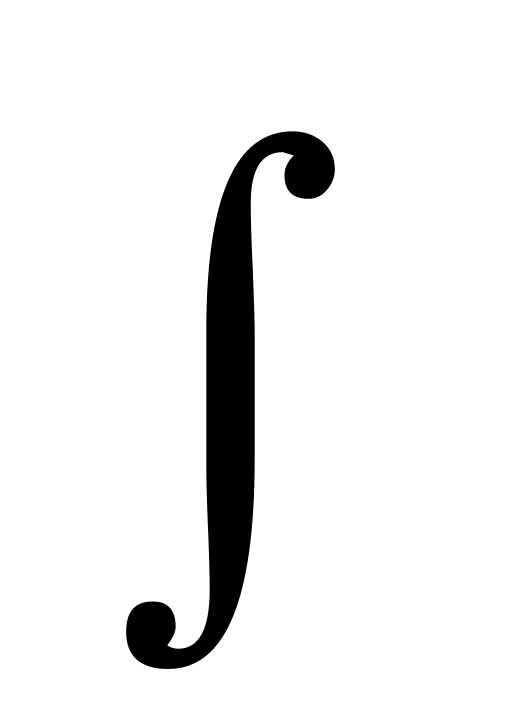 cosxdx = sinx +C ;
cosxdx = sinx +C ; 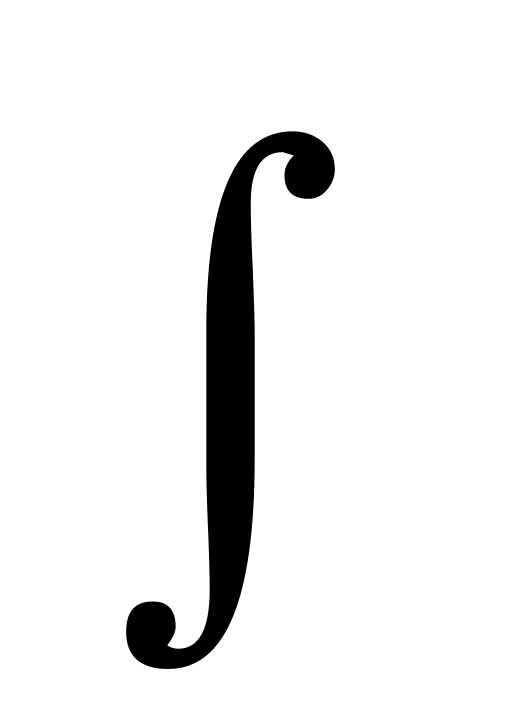 xdx= x
xdx= x /2
/2
Для того, чтобы проверить, правильно ли выполнено интегрирование, надо взять производную от результата и убедиться, что получена подынтегральная функция f(x). Как и всякая обратная операция, интегрирование более сложное действие чем дифференцирование.
Основные свойства неопределенного интеграла:
а). Производная неопределенного интеграла равна подынтегральной
Функции (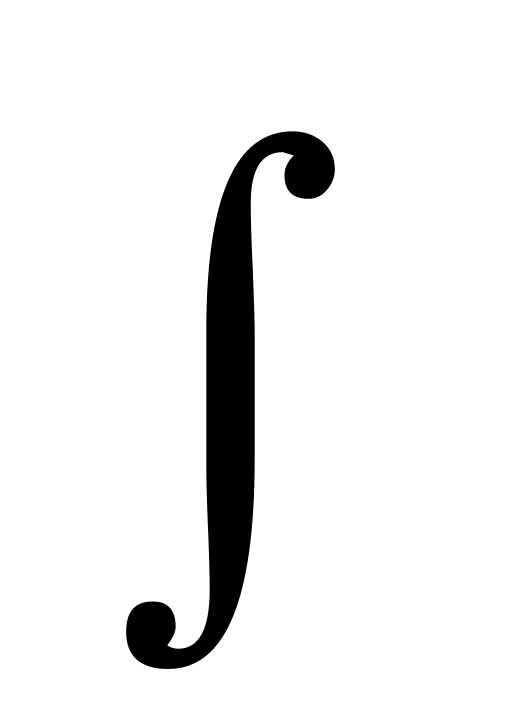 f(x)dx)' = f(x); .
f(x)dx)' = f(x); .
б). Неопределенный интеграл от алгебраической суммы функций равен сумме интегралов от слагаемых функций 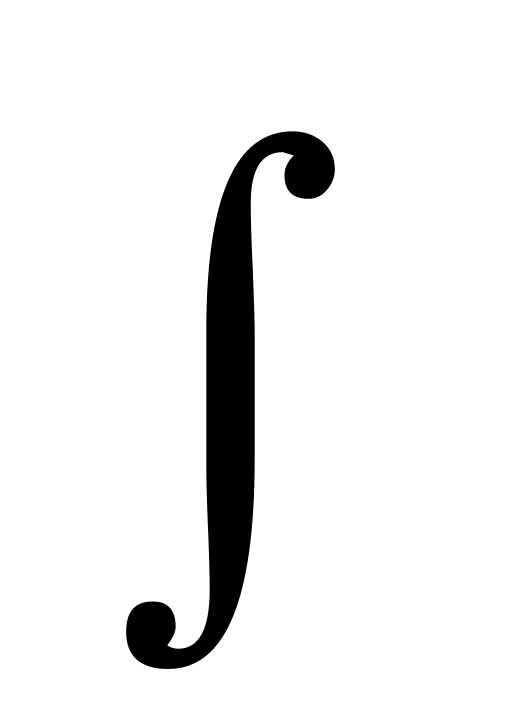 (f
(f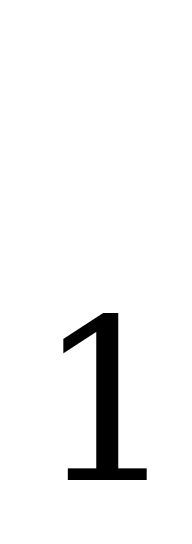 (x) + f
(x) + f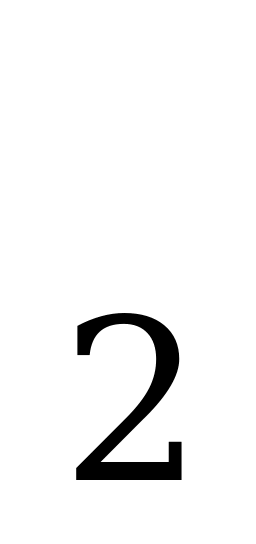 (x))dx =
(x))dx = 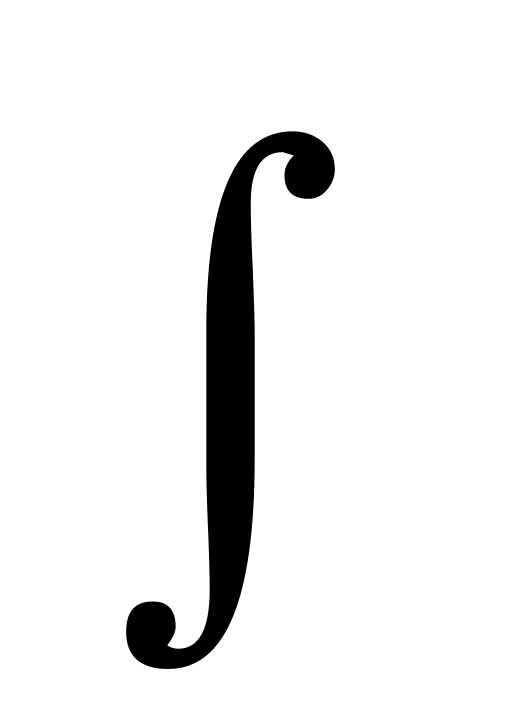 f
f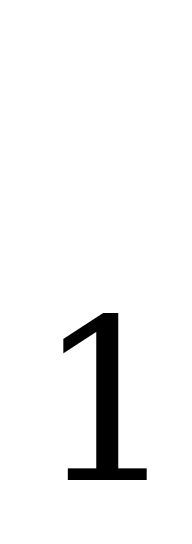 (x) +
(x) + 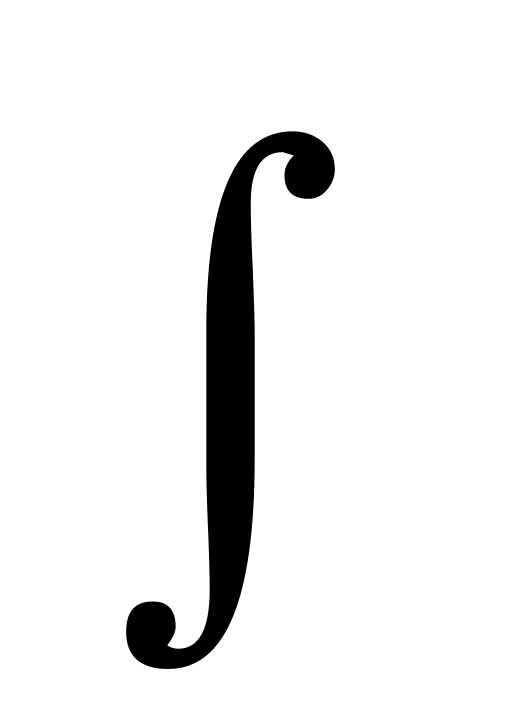 f
f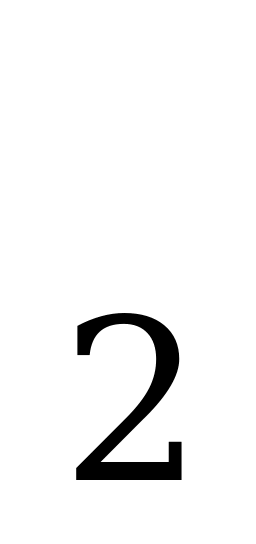 (x);
(x);
в). Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то 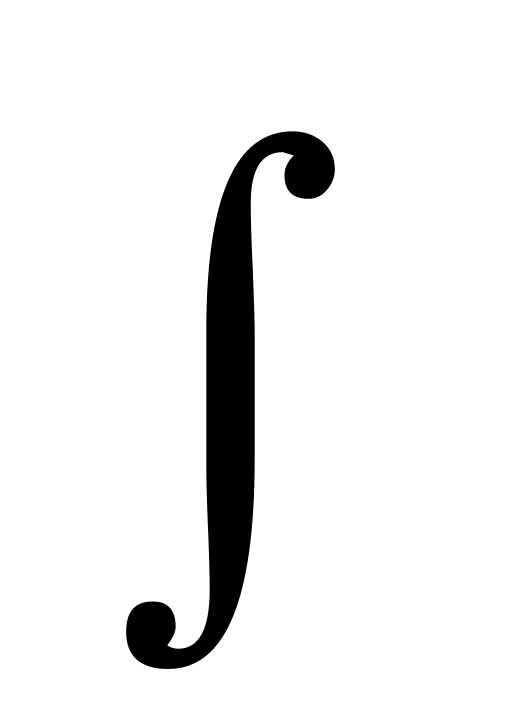 k f(x)dx) = k
k f(x)dx) = k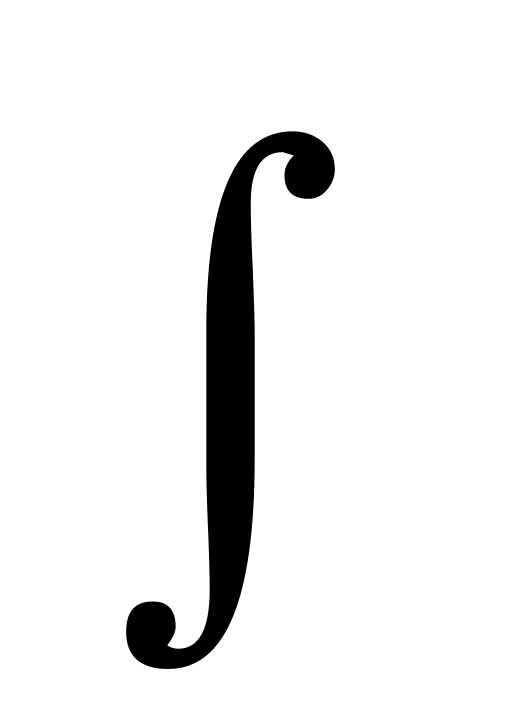 f(x)dx).
f(x)dx).
г)Если F(x) есть первообразная f(x), то 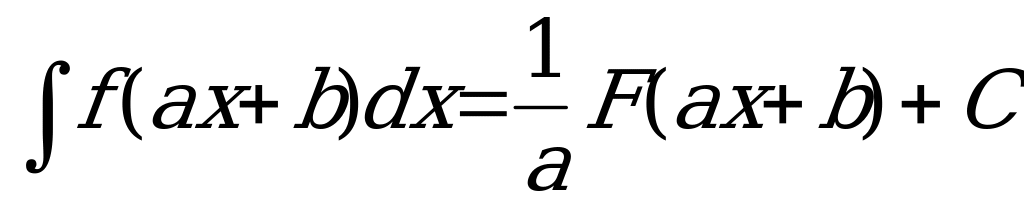
3. Таблица неопределенных интегралов:
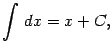
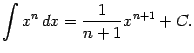
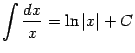
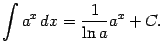
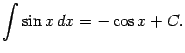
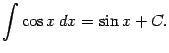
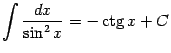
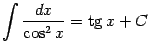
8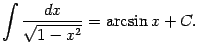 .
.
9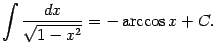 .
.
1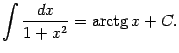 0.
0.
1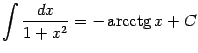 1.
1.
12.
1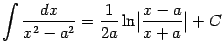 3.
3.
Интегралы содержащие в этой таблице называются табличными.
4. Методы интегрирования:
Непосредственным интегрированием называется способ вычисления неопределенных интегралов с помощью тождественных преобразований подынтегральной функции и применения свойств неопределенных интегралов.
Пример1. 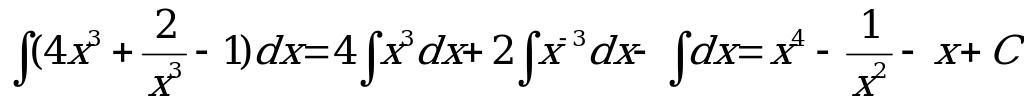
Пример2. 
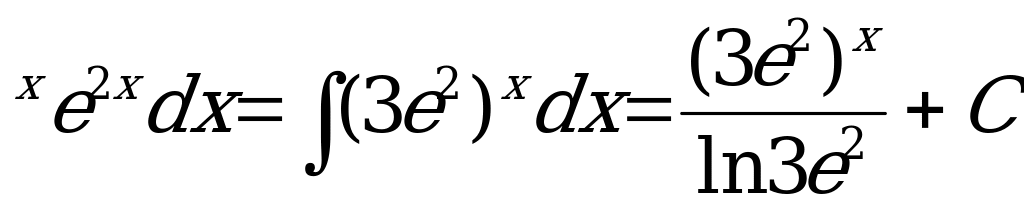
В основе метода лежит утверждение о независимости вида неопределенного интеграла от выбора аргумента, то есть если 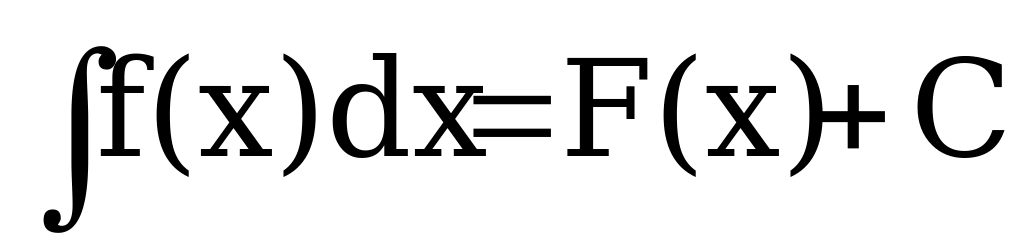 , то для любой непрерывно дифференцируемой функции U= h(x) также существует неопределенный интеграл, причем
, то для любой непрерывно дифференцируемой функции U= h(x) также существует неопределенный интеграл, причем 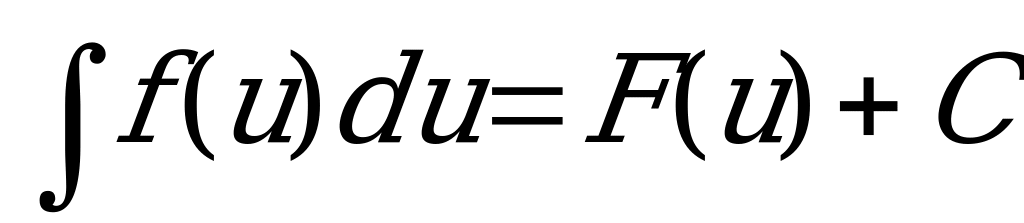 .
.
Таким образом, получаем формулу интегрирования подстановкой:
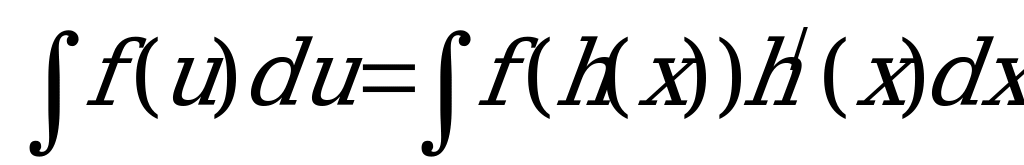 , где U = h(x).
, где U = h(x).
Пример1. 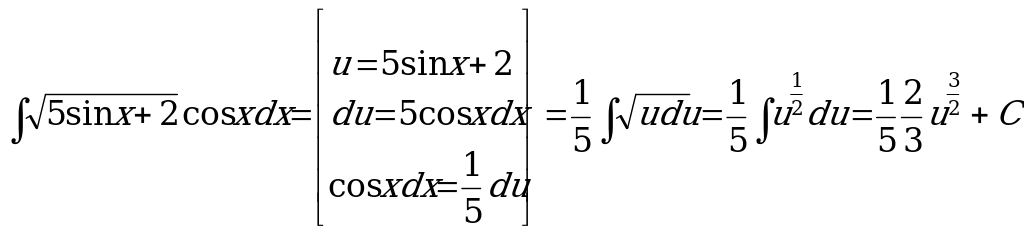 , делаем обратную подстановку и таким образом:
, делаем обратную подстановку и таким образом:
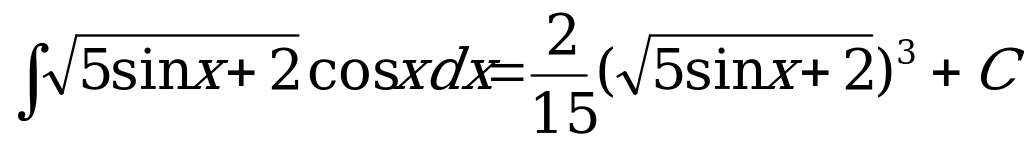
Пример2. 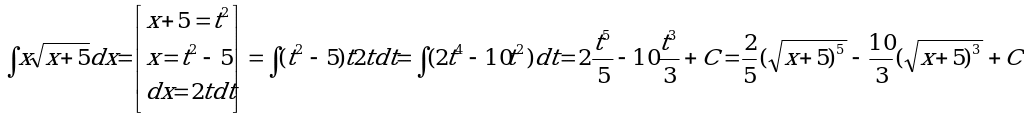
Пусть U(x) и V(x) функции аргумента х, имеющие производные U' и V' .
Формула интегрирования по частям:
 UdV = UV -
UdV = UV - 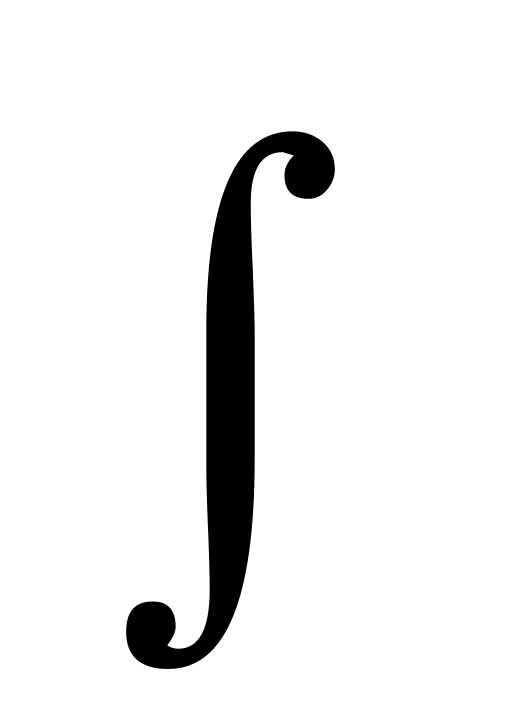 VdU
VdU
Этот метод целесообразно выполнять, когда имеется произведение алгебраического многочлена на элементарную функцию.
Порядок применения формулы интегрирования по частям:
Выбор U и DV
Нахождение DU 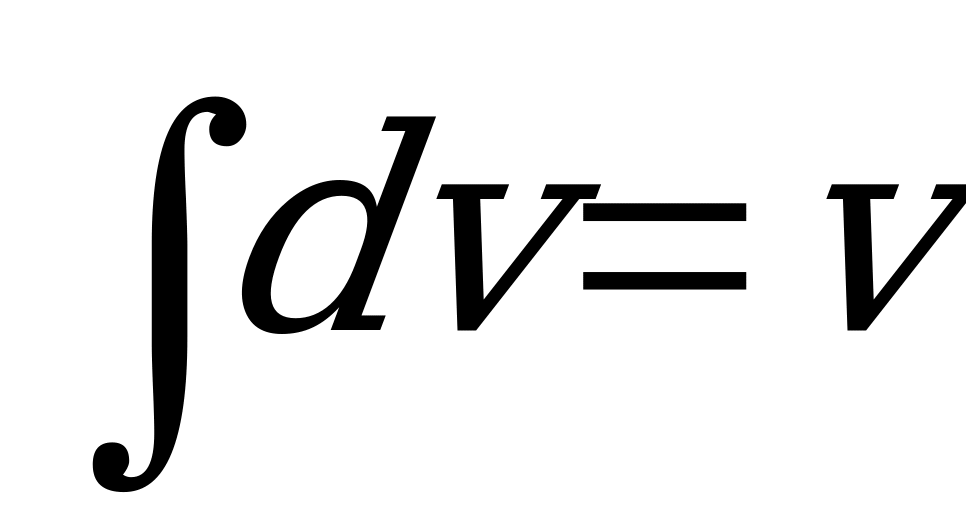 (без учета постоянной С)
(без учета постоянной С)
Применение формулы интегрирования по частям.
Поскольку под знаком интегрирования стоит обычно произведение 2-х функций, то иногда бывает трудно сделать выбор U и V. В этом случае можно воспользоваться простым правилом.
Правило: В качестве функции U выбирается та из функций, которая при дифференцировании упрощается больше, а в качестве V выбирается та из функций, которую легче внести под знак дифференциала. Например: 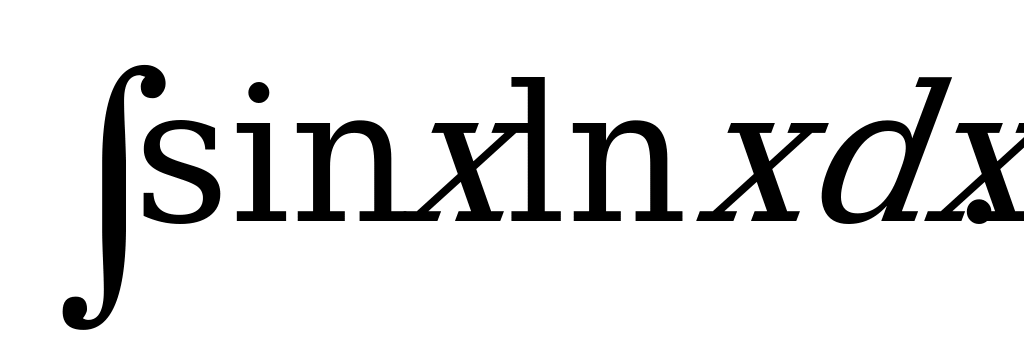 sinxdx = - cosx, но lndx=?. Поэтому dv=sinx dx.
sinxdx = - cosx, но lndx=?. Поэтому dv=sinx dx.
Пример: 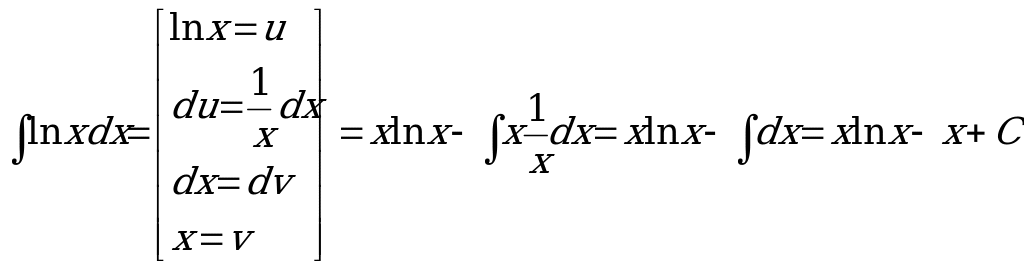







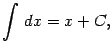
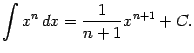
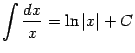
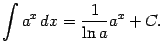
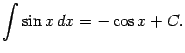
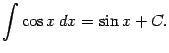
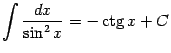
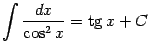
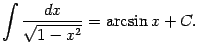 .
.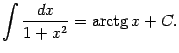 0.
0.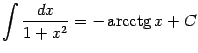 1.
1.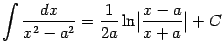 3.
3.