Одномерные отображения
Неподвижная точка — точка, кот зад отобр переводит в неё же, иными сл, реш ур .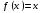
К прим, отобр 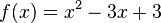 имеет неподв точки x=1 и x=-3, т к f(1)=1 и f(3)=3.
имеет неподв точки x=1 и x=-3, т к f(1)=1 и f(3)=3.
Неподв есть не у всякого отобр — например, отобр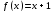 вещ прямой в себя непод точек не имеет.
вещ прямой в себя непод точек не имеет.
Периодические точки - Точки, возвращающиеся в себя после конечного числа итераций, т е, решение ур 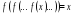
неподвижные точки — это периодические точки периода 1).
Теорема Шарковского. Пусть I – отрезок на числовой прямой, а f: I → I – непрерывное
отображение. Если f имеет точку периода p и 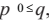 , то найдется точка периода q
, то найдется точка периода q
Пр1.Непрерывное отображение f: [1,5] → [1, 5], имеющее период 5, но не имеющее периода 3 Пусть f задано в точках 1, 2, 3, 4, 5 так : 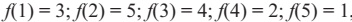
а на промежуточные отрезки распространено по линейности (рис). а на промежуточные
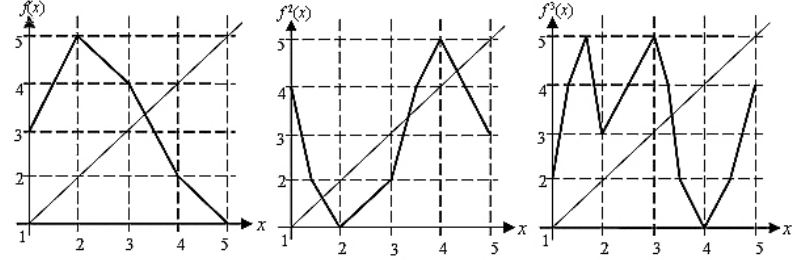
отрезки распространено по линейности (рис. 1). Орбита точки x = 1 имеет вид 1, 3, 4, 2, 5, 1, …, т. е. f обладает периодом 5. Из графиков  видим что нет орбиты периода 3
видим что нет орбиты периода 3
пр2 Непрерывное отображение f: [1,7] → [1, 7], спериод 7, не имеющее периоды 5 и 3.
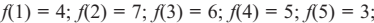
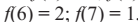
Орбита точки x = 1 имеет вид 1, 4, 5, 3, 6, 2, 7, 1, т е имеет период 7
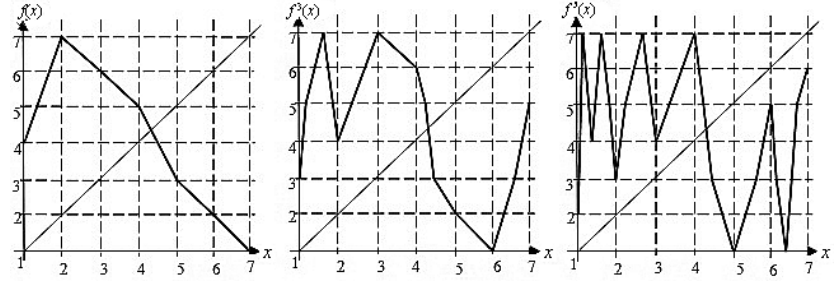
Из последнего рис решение уравнения 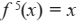 есть только неподвижная точка. Значит, точек предыдущих периодов нет.
есть только неподвижная точка. Значит, точек предыдущих периодов нет.
Задачи на одномерные отображения
пр Найти неподвижную точку отображения промежутка [0, 1] в себя, заданного ф-лой:
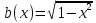
РЕШ: Неподвижная точка отображения промежутка [0, 1] соотв т пересеч графика
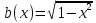 с биссектрисой коорд угла
с биссектрисой коорд угла 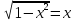
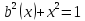
графиком явл окружность в ц нач к=т и с рад = 1ед измерения Неподвижная точка получ путем поворота т (1; 0) на угол 45◦, вокруг центра
1)Функция y = sign x не имеет обратной.
2) Дано уравнение 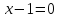 преобразуем его к виду
преобразуем его к виду 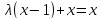 Найдите все , при которых применение теоремы возможно на отрезке [0,2]. Отв: -2
Найдите все , при которых применение теоремы возможно на отрезке [0,2]. Отв: -2
3) Для каждого из следующих множеств указать пример непрерывного отображенияч этого множества в себя без неподвижных точек:
а) числовая прямая; б) полуинтервал (0,1]; в) пара отрезков [-2,-1] и [1,2].
4) указать пример разрывного (т.е. не непрерывного) отображения отрезка [0,1] в себя, не имеющего неподвижных точек
5)На числовой прямой R заданы функции. Какая из них отображает отрезок [0,1] в себя?
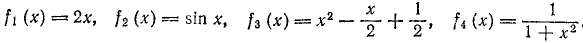
6) Пусть f – непрерывная функция на отрезке 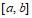 , отображающая каждый конец отрезка в себя, т. е.
, отображающая каждый конец отрезка в себя, т. е. 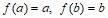 . Пусть g – непрерывная функция, отображающая отрезок
. Пусть g – непрерывная функция, отображающая отрезок 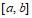 в себя. Докажите, что тогда на этом отрезке найдется такая точка x0, что
в себя. Докажите, что тогда на этом отрезке найдется такая точка x0, что 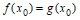 . Сохранится ли это в силе, если g – произвольная непрерывная функция на
. Сохранится ли это в силе, если g – произвольная непрерывная функция на 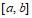 ?
?
7). Докажите, что непрерывное отображение f отрезка 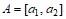 на (весь) отрезок
на (весь) отрезок  , содержащий в себе отрезок А, имеет неподвижную точку. Верно ли это, если образ
, содержащий в себе отрезок А, имеет неподвижную точку. Верно ли это, если образ  отрезка А не совпадает с В, а только лежит в нем?
отрезка А не совпадает с В, а только лежит в нем?
8).Пусть f –непрерывное отображение отрезка 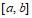 на себя. Докажите, что отображение
на себя. Докажите, что отображение  (композиция отображения f с самим собой) имеет по крайней мере две неподвижных точки. Верно ли это, если f отображает отрезок
(композиция отображения f с самим собой) имеет по крайней мере две неподвижных точки. Верно ли это, если f отображает отрезок 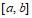 в себя, но не на себя?
в себя, но не на себя?
9) Показать, что отображение  оси Ох в себя имеет единственную неподвижную точку. В качестве приближенного значения корня уравнения
оси Ох в себя имеет единственную неподвижную точку. В качестве приближенного значения корня уравнения  взять 3й член посл-ти
взять 3й член посл-ти  , полученной методом итерации, и оценить величину погрешности.
, полученной методом итерации, и оценить величину погрешности.
10) Отображение А на полупрямой  переводит каждую точку
переводит каждую точку  в
в  . Является ли оно сжимающим и имеет ли неподвижную точку?
. Является ли оно сжимающим и имеет ли неподвижную точку?
Логистическое отображение (квадратичное отображение) - это полиномиальное отображение, описывающее изменение численности популяции с течением времени. 2 вида записи
| Отобр Фейгенбаума | отобр Ферхюльста |
| | |
описывает два эффекта:
1)когда численность популяции xn мала, она размножается со скоростью, пропорциональной этой численности, т к если 
2) скорость размножения падает, возрастает конкуренция и смертность (нелинейное ограничение роста  ) :
) :
1)Найдите неподвижные точки логистического отображения и иссл их устойивость в зависимости от λ отв  и
и
2). Найдите в явном виде элементы 2- цикла логистического отображения В каком интервале параметра λ существует 2й- цикл ?
3)Построить с помощью компьютера итерационные диаграммы для логистического отображения для значений параметра  Какой процесс будет устанавливаться в каждом случае по прошествии достаточно большого времени ?
Какой процесс будет устанавливаться в каждом случае по прошествии достаточно большого времени ?
7)пример разрывного (т.е. не непрерывного) отобр отр [0,1] в себя, не имеющ неподвижных точек.
Инволюции
Непрерывное отображение f отрезка [0,1] в себя называют инволюцией, если  оставляет неподв каждую точку отрезка. Иначе, это значит, что функция f обратна самой себе.
оставляет неподв каждую точку отрезка. Иначе, это значит, что функция f обратна самой себе.
-----------------------------------------------------------------------------------------------------------------
1)Проверить что следующие функции являются инволюциями
2)Доказать что каждая нетривиальная инволюция имеет только 1 непод точку
3)Пусть f – непрерывная функция на отрезке  , отобр каждый конец отрезка в себя, т.е.
, отобр каждый конец отрезка в себя, т.е.  . Пусть g – любая непрер функция, отобр отрезок
. Пусть g – любая непрер функция, отобр отрезок  в себя. До, что тогда на этом отрезке найдется такая т x0, что
в себя. До, что тогда на этом отрезке найдется такая т x0, что  . Сохранится ли это утверждение в силе, если g – произвольная непрерывная функция на
. Сохранится ли это утверждение в силе, если g – произвольная непрерывная функция на  ?
?
Теорема о неподвижной точке.
Допустим, что некоторый шар заполнен песком. Если мы встряхнем этот шар, то все песч немн изменят свое положение. Но, оказывается, что есть такая песчинка, которая останется неподвижной.Пусть А – отрезок тонкой резинки. Б его деформир как уг, но без разрывов и склеивания. И в таком деформир виде заставим его занимать на пл=ти то же место, что и раньше (или часть места). Оказ, что при этом хотя бы одна точка займёт свое первона место.
Эти 2 примера дают понятие т о неподвижной точке. Л.Брауэра и причис к важн т в матем. Ещё прим этой т: если круг повернуть вокруг ц на угол 30о, то единств неподв точкой б центр круга.Но если то же отобр рассм на окружн, то она не б иметь неподвижных точек.
Каждое пост отобр произв пр=ва в себя имеет одну неподвижную т. А отобр некот множества в себя м иметь, а может и не иметь этой точки.
: Точка х, обл свойством, что f(x)=x, наз неподвижной точкой отображения.
Т БРАУЭРА: Каждое непрерывное отображение прямолинейного отрезка в себя имеет хотя бы 1 неподвижную точку.
Интуитивное доказательство
ДОК: В на прямой, содержащей этот отрезок, к-ты так, что отрезок превр в замкн промеж [a, b].
Тогда рассматриваемое отображение будет непрерывной функцией f, отображающей промежуток в себя (f :[a,b]→[a,c]). Опр новую ф q:[a,b]→R с усл, что q(x)=f(x) –x для x € [a,b] . Таким обр, функция q равна, взятому с определенным знаком, расстоянию между точкой Х и её образом f(x).
Если f(x) x, то f(x) - x= q 0, а если f(x)
а) Если неподвижен какой-н из концов промежeжутка, то доказывать нечего, т.к. этот конец и будет неподвижен точно.
б) Доп, что ни один из концов промежутка не неподвижен. Т к f(a) и f(b) принадлежат [a,b], то f(a)a и f(b)0 (f(a) – а = q0) и q (b)
Функция q непрерывна= она принимает все значения между q(a) и q(b). Следовательно, в некой точке х € [a, b] функция g(х) = 0. Эта точка и является искомой неподвижной точкой отображения .Ч т д.
Т Бореука-Улама для окружности. Пусть f : C R - непрерывная функция на окружности C. Тогда существует пара точек - антиподов x, x* такая, что f (x) = f (x*).
Следствие: на любой большой окружности земного шара (например, на экваторе) найдется пара антиподов, в которых температура воздуха одинакова.
Т (о блинах). Если A и B - ограниченные фигуры на плоскости, то существует прямая, которая делит каждую из этих фигур на две части равной площади.
Итерационный метод как применение сжатых отображений
Метод простой итерации - для уточнения корня уравнение f(x) = 0 (1) заменяется эквивалентным уравнением  (2) Т е из
(2) Т е из  следует
следует  и наоборот. Привести (1) к (2) можно многими способами, например,
и наоборот. Привести (1) к (2) можно многими способами, например,  , где
, где  - непрерывная произвольная знакопостоянная функция. Геометрически на интервале отделения корня уравнение (1) представляется в виде двух пересекающихся линий
- непрерывная произвольная знакопостоянная функция. Геометрически на интервале отделения корня уравнение (1) представляется в виде двух пересекающихся линий  и y = x
и y = x
Условия сходимости достаточное f(x)- непрерывно дифференцируемая,  при этом
при этом  должна переводить отрезок [a,b] в себя.
должна переводить отрезок [a,b] в себя.
Итерационная последовательность 
Пример найти корень уравнения  на отрезке [0,1]
на отрезке [0,1]
1 способ 
 но
но  не непрерывно дифференцируема на [0,1]
не непрерывно дифференцируема на [0,1]
Условие сжимаемости не выполнено
2 способ  переводит [0,1] в себя и
переводит [0,1] в себя и 
Условие сжимаемости выполнено
Непрерывные отображения на квадрате
Задается уравнениями 


Интуитивное доказательство теоремы Брауэра
Теорема о неподвижной точке формулируется для отрезка, квадрата. Она верна для круга и всякого выпуклого многоугольника
Лемма Шпернера — комбинаторный аналог теоремы Брауэра о неподвижной точке, один из основных результатов комбинаторной топологии. Утверждает, что при любой Шпернеровской раскраске вершин в триангуляции n-мерного симплекса найдётся ячейка триангуляции, вершины которой покрашены во все цвета. В 1мер сл, лемма Шпернера м рассм как дискр аналог т Больцано Коши.- если большой отрезок разбит на подотр и в вершинах отр расст 1 и 2, то при усл, что в верш большого отрезка стоят разные зн, сущ отрезок подразби, в верш кот стоят разные зн.
Есть триангуляция треугольника T. Вершины отмечены числами 1, 2 и 3 соот. Все вершины триангуляции от этими же числами с соблюдением след граничных условий: если такая вершина лежит на стороне треугольника T, то она получена в качестве отметки одно из тех 2 чисел, кот соотв концам этой стороны. Тогда есть хотя бы 1 грань с 3 разными отметками вершин (хорошая грань). Есть нечетное число хороших граней. , возможны пути 3 типов: 1) от гранич ребра (1,2) к хорошей грани (или в обратном направлении, что несущ), 2) от гранич ребра (1,2) к др такому же ребру, 3) от хорошей грани к другой такой же грани
Задачи на двумерные отображения и неподвижные точки
6) . К остову треугольника (рис.) применяется одно из следующих отображений: 1) каждый угол треугольника, состоящий из 4 граней, загибается внутрь, 2) весь треугольник поворачивается вокруг центра на угол 120 против часовой стрелки. В каждом из этих слу найтит неподвижные и почти неподвижные точки
двумерное отображение Эно
может служить для описания динамики ряда простых физических систем, таких как частица в вязкой среде под действием импульсных толчков, интенсивность которых зависит от координаты.
Параметр b характеризует степень диссипативности Параметр a -нелинейность (эквивалентен параметру λ в отображении Фейгенбаума).
1) Найти неподвижные точки отображения Эно
Отв
2) При выполнении какого условия в отображении появляются устойчивая и неустойчивая точки?
двумерное отображение с кубической нелинейностью Холмса
1. Найти аналитически координаты неподвижных точек периода 1 двумерного отображения Холмса и определить область их существования
метод простой итерации для системы двух уравнений
Рассмотрим систему двух уравнений
разными способами преобразуем к виду
Итерационный процесс
Достаточные условия сходимости
ф)(х, у) и ф2(х, у) определены и непрерывно дифференцируемы в заданной области;
начальные приближения х0, у0 и все последующие х,„ у„ принадлежат заданной области;
в рассматриваемой области выполняются неравенства:
или
Пример решить систему 2 уравнений
Преобразуем
Ограничимся положительным решением. Из рис за начальное приближение положительного решения системы можно принять
Точное решение системы имеет вид
Литература
1)Шашкин. Неподвижные точки, сер. Популярные лекции по математике, М.Наука,1989
2) Прошин Ю.Н., Шакиров М.А., Моделирование и визуализация нелинейных динамических систем, КФУ, Институт физики, 2017 г
3) Лемма Шпернера и справедливое деление, автореферат дипломной работы, СГУ им Чернышевского, каф. Компьютерной алгебры и теории чисел, Свратов, 2017
4) Данилов В.И., Лекции о неподвижных точках. —Российская экономическая школа, М, 2006 г
5) А.П. КузнецовА.В. Савин Л.В. Тюрюкина Введение в физику нелинейных отображений
6) Старостина В.В., Тепляков В.В. Вокруг теоремы Шарковского







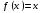
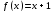 вещ прямой в себя непод точек не имеет.
вещ прямой в себя непод точек не имеет. 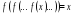


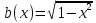
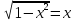
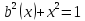
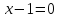 преобразуем его к виду
преобразуем его к виду 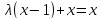 Найдите все , при которых применение теоремы возможно на отрезке [0,2]. Отв: -2
Найдите все , при которых применение теоремы возможно на отрезке [0,2]. Отв: -2 


















