Определенный интеграл
Определение определенного интеграла
Пусть функция  определена на отрезке [a, b], ab. Разобьем этот отрезок на n произвольных частей точками
определена на отрезке [a, b], ab. Разобьем этот отрезок на n произвольных частей точками  . В каждом из полученных частичных отрезков
. В каждом из полученных частичных отрезков  выберем произвольную точку
выберем произвольную точку  и составим сумму
и составим сумму 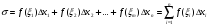 где
где 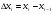 . Сумма вида (1) называется интегральной суммой для функции
. Сумма вида (1) называется интегральной суммой для функции  на [a, b].
на [a, b].
Обозначим через  длину наибольшего частичного отрезка разбиения:
длину наибольшего частичного отрезка разбиения: 
Определение. Если существует конечный предел I интегральной суммы (1) при 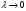 , то этот предел называется определенным интегралом от функции
, то этот предел называется определенным интегралом от функции  по отрезку [a, b] и обозначается следующим образом:
по отрезку [a, b] и обозначается следующим образом:
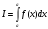 или
или 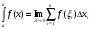
В этом случае функция  называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования,
называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования,  - подынтегральной функцией,
- подынтегральной функцией,  - переменной интегрирования.
- переменной интегрирования.
Для интегрируемости функции достаточно непрерывности функции на отрезке [a, b].
Пример 7. Используя определение, вычислить интеграл
 , где C – некоторое число.
, где C – некоторое число.
Решение. Разобьем отрезок [a, b] на n произвольных частей точками  и составим соответствующую интегральную сумму (1). Так как подынтегральная функция
и составим соответствующую интегральную сумму (1). Так как подынтегральная функция  постоянна, то для любого выбора промежуточных точек
постоянна, то для любого выбора промежуточных точек  получим интегральную сумму вида
получим интегральную сумму вида 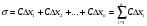 . Далее имеем
. Далее имеем

Видим, что интегральная сумма для данной функции не зависит ни от разбиения, ни от выбора точек,  и равна С(b-a). Следовательно, и ее предел при
и равна С(b-a). Следовательно, и ее предел при 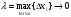 равен той же величине.
равен той же величине.
Таким образом, по определению,

Геометрический смысл определенного интеграла.
Если функция  непрерывна и неотрицательна на отрезке [a, b], где ab, то определенный интеграл
непрерывна и неотрицательна на отрезке [a, b], где ab, то определенный интеграл  геометрически представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции
геометрически представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции  , снизу отрезком [a, b] оси OX, а с боков отрезками прямых x=a, x=b.
, снизу отрезком [a, b] оси OX, а с боков отрезками прямых x=a, x=b.

Основные свойства определенного интеграла:
По определению 
По определению 
Каковы бы ни были числа a, b, c, всегда имеет место равенство

Постоянный множитель можно выносить за знак определенного интеграла, т. е.

Постоянный множитель от алгебраической суммы функции равен алгебраической сумме их интегралов, т. е. 
Следствие (оценка определенного интеграла)
Если функция 
 , то
, то  .
.
Метод “интегрирования” определенных интегралов
Формула Ньютона-Лейбница
Если функция  непрерывна на отрезке [a, b] и F(x)- первообразная функции
непрерывна на отрезке [a, b] и F(x)- первообразная функции  на этом отрезке, то
на этом отрезке, то

Пример 8. Вычислить
Решение: .
Интегрирование заменой переменной
Теорема: Пусть выполняются следующие условия.
тогда  .
.
Пример 9. Вычислить интеграл:  .
.
Решение:
Интегрирование по частям
Теорема: Пусть  определены на отрезке [a, b], тогда
определены на отрезке [a, b], тогда

Пример 10. Вычислить интеграл: 
Решение:
Геометрические приложения определенного интеграла
Вычисление площадей плоских фигур.
Площадью криволинейной трапеции, ограниченной кривой  и прямыми
и прямыми  и отрезком [a, b] оси OX вычисляется по формуле:
и отрезком [a, b] оси OX вычисляется по формуле:
a. 

b. 

Площадь фигуры, ограниченной кривыми  и
и  (таких, что
(таких, что  ) и прямыми
) и прямыми  и отрезком [a, b] оси OX вычисляется по формуле
и отрезком [a, b] оси OX вычисляется по формуле

Пример 11. Найти площадь фигуры, ограниченной линиями  и
и  .
.
Решение:
Вычисление длины дуги плоской кривой.
Если кривая  на отрезке [a, b] гладкая (то есть
на отрезке [a, b] гладкая (то есть  ), то длина соответствующей дуги этой кривой находится по формуле
), то длина соответствующей дуги этой кривой находится по формуле

Вычисление объемов тел вращения.
Если криволинейная трапеция, ограниченная кривой  и прямыми
и прямыми  , вращается вокруг оси OX, то объем тела вращения вычисляется по формуле
, вращается вокруг оси OX, то объем тела вращения вычисляется по формуле

Формально заменяя в формуле переменную x на y получим формулу для вычисления объема тела, полученного от вращения криволинейной трапеции вокруг оси OY

Если трапеция ограничена прямыми  , то
, то  .
.
Площадь поверхности вращения.
Если дуга гладкой кривой  вращается вокруг оси OX, то площадь поверхности вращения вычисляется по формуле
вращается вокруг оси OX, то площадь поверхности вращения вычисляется по формуле
 .
.
Контрольные вопросы
Что называется первообразной для функции f(x) на промежутке x.
Что называется неопределенным интегралом.
Свойства неопределенного интеграла.
Метод замены переменной в неопределенном интеграле.
Метод интегрирования по частям.
Что называется разбиением отрезка.
В чем заключается геометрический смысл определенного интеграла.
Свойства определенного интеграла.
Формула Ньютона – Лейбница.
Интегрирование заменой переменной.
Интегрирование по частям.
Как вычисляются площади плоских фигур.
Как вычисляется длина дуги плоской кривой.
Как вычисляются объемы тел вращения вокруг осей.
Как вычисляется площадь поверхности вращения.







 определена на отрезке [a, b], ab. Разобьем этот отрезок на n произвольных частей точками
определена на отрезке [a, b], ab. Разобьем этот отрезок на n произвольных частей точками  . В каждом из полученных частичных отрезков
. В каждом из полученных частичных отрезков  выберем произвольную точку
выберем произвольную точку  и составим сумму
и составим сумму 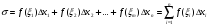 где
где 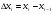 . Сумма вида (1) называется интегральной суммой для функции
. Сумма вида (1) называется интегральной суммой для функции  длину наибольшего частичного отрезка разбиения:
длину наибольшего частичного отрезка разбиения: 
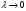 , то этот предел называется определенным интегралом от функции
, то этот предел называется определенным интегралом от функции 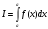 или
или 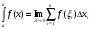
 - переменной интегрирования.
- переменной интегрирования. , где C – некоторое число.
, где C – некоторое число. постоянна, то для любого выбора промежуточных точек
постоянна, то для любого выбора промежуточных точек  получим интегральную сумму вида
получим интегральную сумму вида 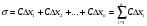 . Далее имеем
. Далее имеем 
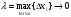 равен той же величине.
равен той же величине.

















