| Логарифмические уравнения |
| Логарифмическим уравнением называется уравнение, в котором неизвестное содержится под знаком логарифма ( в частности, в основании логарифма). Простейшее логарифмическое уравнение имеет вид: 1. logaf(x) = b, используя определение логарифма получим f(x) = ab Решение любого логарифмического уравнения предполагает переход от логарифмов к выражениям, стоящим под знаком логарифмов. 2. logaf(x) = logag(x) Сделать равносильный переход от исходного уравнения к системе, включающей область допустимых значений уравнения: 1.f(x) = g(x) и f(x)0 или 2. f(x) = g(x) и g(x)0, в зависимости от того, какое неравенство проще. 3.Если уравнение содержит неизвестное в основании логарифма: l oga(x)f(x) = loga(x)g(x),то мы переходим к системе: f(x) = g(x) oga(x)f(x) = loga(x)g(x),то мы переходим к системе: f(x) = g(x) g(x) 0 a(x ) 0 a(x) ≠ 1 4. Отдельно найти область допустимых значений уравнения, затем решить уравнение и проверить, удовлетворяют ли найденные решения ОДЗ уравнения.
5. Решить уравнение, и потом сделать проверку: подставить найденные решения в исходное уравнение, и проверить, получим ли мы верное равенство. |
| Внимание! Мы всегда ищем ОДЗ исходного уравнения, а не того, которое получится в процессе преобразований. То есть ОДЗ записываем перед тем, как переходим к решению уравнения. |
| Вид уравнения | Метод решения | Примеры |
| 1.log a f(x)=b, где a 0, а ≠ 1, f(x) 0 Применение определения логарифма: f(x) = ab. log (x+1)(2x2+1) =2. Найдем ОДЗ уравнения:  (х+1) 0 х -1 (х+1) 0 х -1 (2x2+1) 0 для любого х ОДЗ : По определению логарифма: (x+1)2 =2x2+1; x2+2x+1 =2x2+1; x2-2x = 0; х(х-2) = 0 х = 0 или х - 2 = 0; x1 = 0; x2 = 2. Из двух полученных корней только корень x2 =2 принадлежит ОДЗ, а x1 =0 не принадлежит ОДЗ и, следовательно, является посторонним корнем. Ответ: x =2. | Решить уравнение: 1. log3(2x+1)=2 По определению логарифма имеем:  1.2х + 3 = 32 1.2х + 3 = 32 2.2х + 3 0 -ОДЗ 3.а = 3 0 , значит основание подходит. 1.2х + 3 = 9, 2х = 9 – 3, 2х = 6, х = 6:2, х=3. 2.2х+30, 2х -3, х -3:2, х -1,5 - ОДЗ Вывод: х=3 принадлежит ОДЗ. Ответ:3. Замечание! Можно было не находить ОДЗ, а сделать проверку корня, подставив его значение х=3 в первоначальное уравнение. 2. log3 (2х-1) = 2 Исходя из определения логарифма, а именно, что логарифм - это число, в которое надо возвести основание, чтобы получить выражение, которое находится под знаком логарифма, т.е. 3 2 = 2х-1 или 2х = 9+1 и х=5
| 1 .log2(3 – 6x) = 3
2. lg(х2 – 2х) = = lg (2х + 12)
3. х lg х = 10000
4. log3x - log3 x = 3
5. log2x – log4x =3
6. log3 x = - x
7. lg (x2 – 2x) = lg(2x + 12)
8. log3 x - 2log � � х = 6 � х = 6 9. log5(2x + 3) = log5(x + 1) |
| 2. loga f(x) = loga g(x)   f(x) =g(x) f(x) =g(x) f(x)0 или  f(x)=g(x) f(x)=g(x) g(x) 0
Уравнения, которые содержат логарифмы только в первой степени. Они с помощью преобразований и использования свойств логарифмов приводятся к виду 2, т.е используется метод потенцирования. Решить уравнение: 1. log x-6(x2-5) =log x-6(2x+19). x2-5 =2x+19; x2-2x-24 =0; x1 =6; x2 =-4. Подставим у уравнение x2 =-4, получим log -4-6((-4)2-5) =log -4-6(2∙(-4)+ + 19). log -1011 =log -10 11, а = -10 , но по определению это невозможно Аналогично проверим второй корень. Учитывая проверку, отметим, что x2 =-4; x1 =6 - посторонний корень. Ответ: решений нет. | Решить уравнение: 1. log5x =log5(6-x2)  Применяя метод потенцирования, получим: Применяя метод потенцирования, получим: x = 6-x2; х 0 x2 + x - 6 = 0;по т .Виета х1∙х2 = -6 .Виета х1∙х2 = -6 х1+х2 = -1, подбором найдём корни x1 =2; x2 =-3. Учитывая ОДЗ, отметим, что x2 =-3 - посторонний корень. Ответ: x =2.
2. log3 (2х-5) = log3х Применяем потенцирование, получаем: 2х-5 = х 2х – 1х = 5 х = 5 ОДЗ находить не будем, а сделаем проверку корня. Подставим х = 5 в первоначальное уравнение log3 (2∙5-5) = log35 log3 5= log35 верное равенство. Ответ: 5. | 
|
| а) loga f(x)+loga g(x)=logah(x)  loga( f(x)∙ g(x)) = logah(x)   ( f(x)∙ g(x)) = h(x) ( f(x)∙ g(x)) = h(x) f(x) 0 g(x) 0 h(x) 0 | Решить уравнение: 1. lg(x+3) =2lg2- lgx Преобразуем: перенесём - lgx из правой части в левую поменяв знак, а 2 внесём в степень числа 2 (2lg2 = lg22). lg(x+3) =lg22-lgx; lg(x+3) + lgx= lg22, применив формулу а). lg((x+3)∙x) = lg22 ((x+3)∙x) = 22 x2 + 3x - 4 = 0, по т. Виета х1∙х2 = -4 , а х1+х2 = -3. Подбором найдём корни: x1 =1; x2 =-4. Учитывая ОДЗ ,т.е , (x+3)0  х -3 отметим, что x2 = -4 - посторонний корень. Ответ: x=1. 1.log2(х+5) = 2log2 (1- х) Преобразуем по формуле в). Имеем: log2 (х+5)= log2 (1- х)2 ОДЗ: х +5 0 или х -5 х+5 = (1 – х)2 или х2-3х-4=0, тогда х1=4, а х2 =-1 Ответ: х1=4, а х2 =-1 | 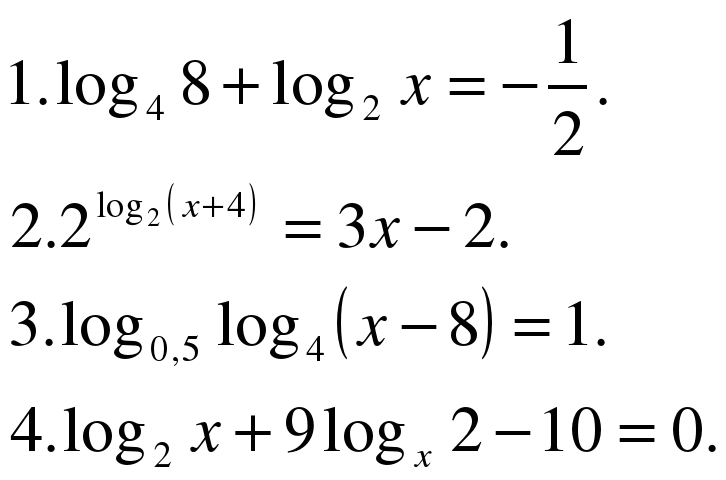
5.log2 (4х + 5) = log2 (9 – 2х) 6.log3 (х² - 5х – 23) =0; 7.lg(x + 2) + lg(x – 2) = lg(5x + +10)
|
| б) loga f(x)-loga g(x)=logah(x)  log a ( f(x):g(x)) = log a h(x) log a ( f(x):g(x)) = log a h(x)  ( f(x) : g(x)) = h(x) ( f(x) : g(x)) = h(x) f(x) 0 h(x) 0 g(x) 0
Из б) всегда можно получить а), перенеся слагаемое в другую часть уравнения. |
| в) nloga f(x)=logah(x)  loga f n(x) =logah(x)  f n(x) = h(x) f n(x) = h(x) f(x) 0 h(x) 0
|
| 3.log2a f(x)+b∙ log a f(x)+c = 0 Пусть log a f(x) = t,тогда log2a f(x ) = t2 и уравнение примет вид t2 + bt + c = 0. Найдём t1 и t2. Затем вернёмся к старой переменной, решив уравнения: 1) log a f(x) = t1 2) log a f(x) = t2 | Решить уравнение: 1. log32x-log3x =2 log32x-log3x – 2 = 0 ОДЗ: x 0. Пусть log3x =у, тогда уравнение примет вид: y2-y-2 =0, по т .Виета у1∙у2 = -2 .Виета у1∙у2 = -2 у1+у2 = 1, подбором найдём корни: y1 =2; y2 =-1. Вернёмся к старой переменной. Т.к log3x =у, то 1)log3x =2; x1 =32; x1 =9; 2)log3x =-1; x2 =3-1; x2 =1/3. Так как x1 0, x2 0 то они принадлежат ОДЗ уравнения и являются его корнями. Ответ: x1 =9; x2 =1/3. |
|
| Важно! Прежде чем вводить замену, нужно «растащить» логарифмы, входящие в состав уравнения на «кирпичики», используя свойства логарифмов. |
| 4.Приведение к одному основанию, если они различные. Решить уравнение: log7x+logx7 =2,5. ОДЗ: x 0, logx7 = log7x +  = = умножим на 2∙ logx7 умножим на 2∙ logx7 2log27x-5 log7x+2 =0 или log27 x-2,5 log7x+1 =0. Пусть log7x =у, тогда y2-2,5y+1 =0; y1 =2; y2 =1/2. 1)log7x =2; x1 = 72 = 49; 2)log7x =1/2; x2 =70,5 =  ; ; Ответ: x1 =49; x2 =  . . | Решить уравнение: 1. log16x+log4x+log2x =7 ОДЗ: x 0. Логарифмы в левой части уравнения приведем к оснаванию 2 по формуле. log16x =log24 x=1/4 ∙log2x; log4x =log2 2x=1/2log2x 1/4log2x)+1/2log2x+log2x =7; (7/4)log2x =7; log2x =7:7/4; log2x = 4 x =24 х =16 0. Ответ: x=16. |
|
| 5.Логарифмирование левой и правой части уравнения по одному и тому же основанию «a», если уравнение имеет вид: х loga g(x) =b | Решить уравнение: х log2х+2 = 8. Прологарифмируем левую и правую части уравнения по основанию 2. Получим log2 (х (log2х+2)) = log2 8, (log2 х + 2) · log2 х = 3. log2 2 х + 2 · log2 х = 3. log2 2 х + 2 · log2 х – 3 = 0 Пусть log2 х = t. t2 + 2t – 3 = 0. t1= -3 t2 = 1 Значит 1. log2 х = 1 и х1 = 2 или 2. log2 х = -3 и х2 =2-3 = 1/8 Ответ: х1 = 2 и х2 =1/8
|
|
| 6.Функционально-графический метод, если уравнение имеет вид: log a f(x) = g(x)

у = log2 x y = 3 – x
Ответ: х = 2 | Строим графики функций у = log a f(x) и у = g(x) Решение – абсцисса ( х) точки пересечения графиков. Решить уравнение: log3 x = 4-x Построим графики функций у = 4 – х и у = log3 x Абсцисса точки пересечения графиков х = 3 есть решение данного уравнения.

|
|





 б)
б)
 og
og (х+1) 0 х -1
(х+1) 0 х -1 1.2х + 3 = 32
1.2х + 3 = 32

 Применяя метод потенцирования, получим:
Применяя метод потенцирования, получим: .Виета х1∙х2 = -6
.Виета х1∙х2 = -6

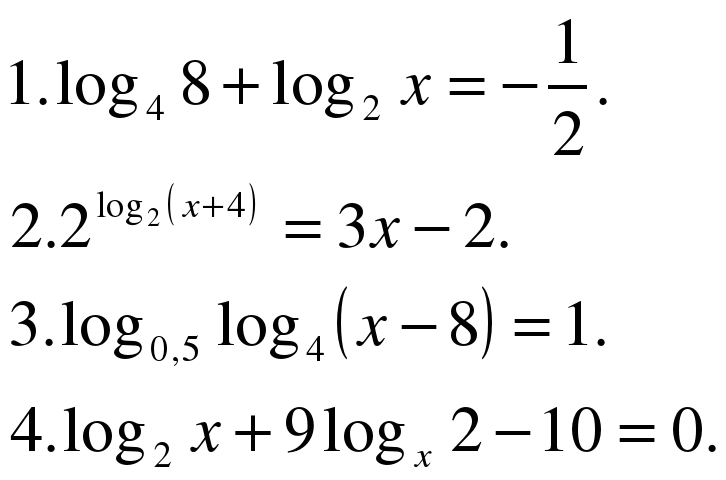


















 (x)
(x)
 5х - 9≤ 3х + 1
5х - 9≤ 3х + 1 

















