| Призма Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники называются основаниям призмы, а отрезки, соединяющие соответствующие вершины, - боковыми ребрами призмы. Так как параллельный перенос есть движение, то основания призмы равны. Так как при параллельном переносе плоскость переходит в параллельную плоскость (или в себя), то у призмы основания лежат на параллельных плоскостях. Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у призмы боковые ребра параллельны и равны. Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. У каждого из этих параллелограммов две стороны являются соответствующими сторонами оснований, а две другие – соседними боковыми ребрами. Высотой призмы называется расстояние между плоскостями ее оснований. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани называется диагональю призмы. Призма называется n-угольной, если ее основания – n-угольник. Изображение: 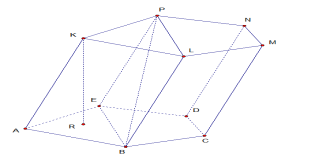 Теорема: Объем любой призмы равен произведению площади ее основания на высоту. Формула. Пусть H – высота произвольной призмы, S –площадь основания, V –объем, тогда: V = SН. Призмой, вписанной в цилиндр, называется такая призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами – образующие цилиндра. 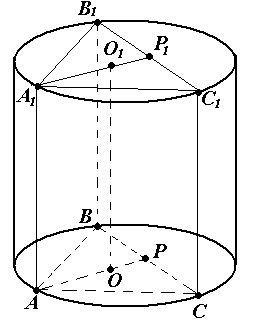 Призмой, описанной около цилиндра, называется призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра. 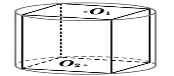
| Прямая призма Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной. 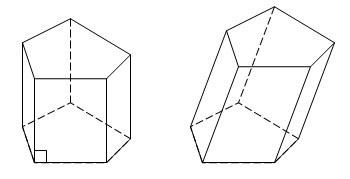 У прямой призмы боковые грани являются прямоугольниками. При изображении прямой призмы на рисунке боковые ребра обычно проводят вертикально. Прямая призма называется правильной, если ее основания являются правильными многоугольниками. Боковой поверхностью призмы (точнее, площадью боковой поверхности) называется сумма площадей боковых граней. Пол-ная поверхность призмы равна сумме боковой поверхности и площадей оснований. Теорема: Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т. е. на длину бокового ребра. Формула. Пусть p – периметр основания прямой призмы, H – высота прямой призмы, Sбок – площадь боковой поверхности прямой призмы, тогда: Sбок = pH. |
| Пирамида Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Пирамида называется n-угольной, если ее основанием является n-угольник. Треугольная пирамида называется также тетраэдром. Теорема: Объем любой пирамиды равен одной трети произведения площади ее основания на высоту: V = 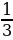 SH. SH. Пирамидой, вписанной в конус, называется такая пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса. Боковые ребра пирамиды, вписанной в конус, являются образующими конуса. 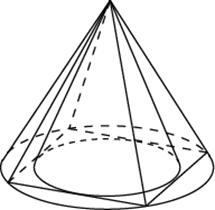 Пирамидой, описанной около конуса, называется пирамида, у которой основанием служит многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса. Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса.
| Правильная пирамида Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника. Осью правильной пирамиды называется прямая, содержащая ее высоту. У правильной пирамиды боковые ребра равны, следовательно, боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. Боковой поверхностью пирамиды называется сумма площадей ее боковых граней. Теорема: Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему. Изображение пирамиды 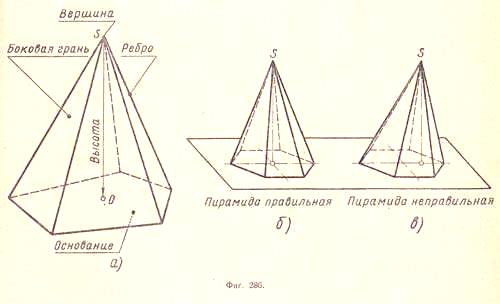 Формула. Пусть р – периметр произвольной пирамиды, l –апофема пирамиды, Sбок – площадь боковой поверхности правильной пирамиды, тогда: Sбок = 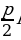 Усеченная пирамида, которая получается из правильной пирамиды, также называется правильной. Боковые грани правильной усеченной пирамиды – равные равнобокие трапеции; их высоты называются апофемами. |
| Прямоугольный параллелепипед Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани – прямоугольники. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом. Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями). У прямоугольного параллелепипеда три измерения. !!!Теорема: В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений. Симметрия прямоугольного параллелепипеда. У прямоугольного параллелепипеда, как у всякого параллелепипеда, есть центр симметрии, проходящее через центр симметрии параллельно граням. Она проходит через середины четырех параллельных ребер параллелепипеда. Концы ребер являются симметричными точками. Если у параллелепипеда все линейные размеры разные, то у него нет других плоскостей симметрии, кроме названных. Если же у параллелепипеда два линейных размера равны, то у него есть еще две плоскости симметрии. Эти плоскости диагональных сечений. 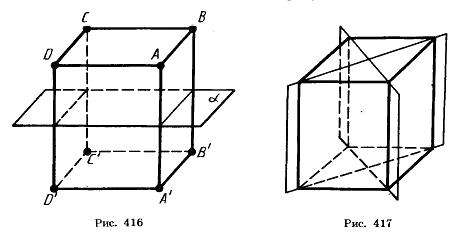 Если у параллелепипеда все линейные размеры равны, т. е. он является кубом, то у него плоскость любого диагонального сечения является плоскостью симметрии. У куба 9 плоскостей симметрии. !!!Теорема: Объем прямоугольного параллелепипеда с линейными размерами а, b, с вычисляется по формуле V = abc. Призма Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn , расположенных в параллельных плоскостях, и n параллелограммов, называется призмой. Перпендикуляр, проведенный из какого-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Прямая призма Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой. Высота прямой призмы равна ее боковому ребру. Прямая призма называется правильной, если ее основания – правильные многоугольники. Теорема: Объем прямой призмы равен произведению площади основания на высоту. Теорема: Объем наклонной призмы равен произведению площади основания на высоту. 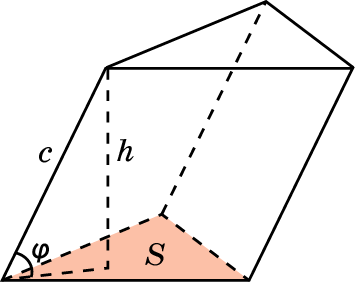 Теорема: Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ему сечению. |
Треугольная пирамида – это тетраэдр. Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т. е. основания и боковых граней), а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней. Sполн = Sбок + Sосн. Теорема: Объем пирамиды равен одной трети произведения площади основания на высоту. Формула. Пусть Н –высота произвольной пирамиды, S – площадь основания, V –объем, тогда: V = 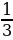 SH. SH. Усеченная пирамида Теорема: Площадь боковой поверхности правильной усеченной пирамиды равна произведению полу-суммы периметров оснований на апофему. Боковые грани усеченной пирамиды – трапеции. Высота этих трапеций называется апофемами. Усеченная пирамида называется правильной, если она получается сечением правильной пирамиды плоскостью, параллельной основанию. Площадью боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней. !!!Теорема: Объем усеченной пирамиды, высота которой равна h, а площадь оснований равны S и S1, вычисляется по формуле V = 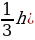 1 + 1 + 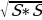 1) 1) |
| Пирамида Рассмотрим многоугольник А1А2…Аn и точку P, не лежащую в плоскости этого многоугольника. Соединив точку P отрезками с вершинами многоугольника, получим n треугольников.: PА1А2, PА2А3,…, PАnА1. Многогранник, составленный из n-угольника А1А2…Аn и n треугольников, называется пирамидой.
Многоугольник А1А2…Аn называется основанием, а треугольники (n) –боковыми гранями пирамиды. Точка P называется вершиной пирамиды, а отрезки PА1, PА2,…, PАn – ее боковыми ребрами. Пирамиду с основанием А1А2…Аn и вершиной P обозначают так: PА1А2…Аn – называют n-угольной пирамидой. | Правильная пирамида Пирамида называется правильной, если ее основание –правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. ( Центром правильного многоугольника называется центр вписанной в него окружности.) Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками. Высота боковой грани правильнойпирамиды, проведенная из ее вершины, называется апофемой. Апофемы правильной пирамиды равны друг другу. Теорема: Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. |
| Параллелепипед Рассмотрим два равных параллелограмма АВСD и А1В1С1D1, расположенных в параллельных плоскостях так, что отрезки АА1, ВВ1 , СС1 и DD1 параллельны (Рис. 35). Четырехугольники АВВ1А1, ВСС1В1, СDD1C1, DАА1D1 также являются параллелограммами, так как каждый из них имеет попарные параллельные противоположные стороны, например, в четырехугольнике АВВ1А1 стороны АА1, ВВ1 параллельны по условию, а стороны АВ и А1В1 – по свойству линей пересечения двух параллельных плоскостей третьей. Поверхность составленная из двух равных параллелограммов АВСD и А1В1С1D1 и четырех параллелограммов, называется параллелепипедом и обозначается так: АВСDА1В1С1D1. 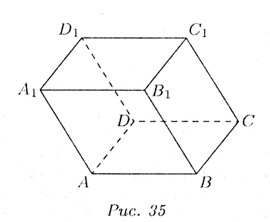 Параллелограммы, из которых составлен параллелепипед, называют гранями, их стороны – ребрами, а вершины параллелограммов – вершинами параллелепипеда. Параллелепипед имеет 6 граней, 12 ребер и 8 вершин. Две грани параллелепипеда, имеющее общее ребро, называются смежными, а не имеющие общих ребер – противоположными. Две вершины, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Каждый параллелепипед имеет 4 диагонали. Часто выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани – боковыми гранями параллелепипеда. Свойства: 10 Противоположные грани параллелепипеда параллельны и равны. 20 Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. | Прямоугольный параллелепипед Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники. Свойства: 10 В прямоугольном параллелепипеде все шесть граней –прямоугольники. Полуплоскости, в которых расположены смежные грани параллелепипеда, образуют двугранные углы, которые называются двугранными углами параллелепипеда. 20 Все двугранные углы прямоугольного параллелепипеда – прямые. Длины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипеда. Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. 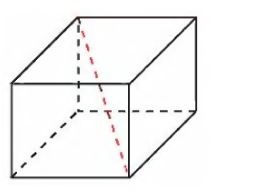 Формула. Пусть d – диагональ прямоугольного параллелепипе-да, а, b, c – его измерения, тогда: d2 = a2+ b2 + c2. Следствие: Диагонали прямоугольного параллелепипеда равны. Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом. Все грани куба – равные друг другу квадраты. Теорема: Объем прямоугольного параллелепипеда равен произведению трех его измерений. Следствие 1: Объем прямоугольного параллелепипеда равен произведению площади основания на высоту. V = abc =Sh. Следствие 2: Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту. |
|
Призма Призма – многогранник, поверхность которого состоит из двух равных многоугольников, называемых основаниями призмы, и параллелограммов имеющих общее стороны с каждым из оснований и называемых боковыми гранями призмы. Многогранником называется тело, поверхность которого состоит из конечного числа многоугольников, называемых гранями многогранника. Стороны и вершины этих многоугольников называются, соответственно, ребрами и вершинами многогранника. Теорема: Около любой прямой призмы можно описать сферу, тогда и только тогда, когда около основания этой призмы можно описать окружность. Теорема: В прямую призму можно вписать сферу тогда и только тогда, когда в основании этой призмы можно вписать окружность и высота призмы равна диаметру этой окружности. Объем наклонной призмы с площадью основания S и высотой h вычисляется по формуле: V =Sh (по учеб. пособию «Геометрия 10-11» И. М. Смирнова) |
Призма. Определение: Призмой называется многогранник, все вершины которого расположены в двух параллельных плоскостях, причем в этих же двух плоскостях лежат две грани призмы, представляющие собой равные многоугольники с соответственно параллельными сторонами, а все ребра, не лежащие в этих плоскостях, параллельны. Боковая поверхность призмы – это совокупность параллелограммов, являющихся ее боковыми гранями. Призма называется правильной, если она прямая, а ее основания – правильные многоугольники. !!!Теорема: (формула для вычисления объема треугольной призмы через площадь боковой грани). Пусть Q – площадь одной из боковых граней треугольной призмы, d – расстояние от противоположного ребра до этой грани. Тогда объем этой призмы может быть найден по формуле V = 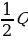 d. ( по учеб. пособию «Геометрия 10-11» И. Ф. Шарыгина) d. ( по учеб. пособию «Геометрия 10-11» И. Ф. Шарыгина)
|
| Усеченная пирамида Пусть плоскость пересекает пирамиду и параллельна ее основании. Часть пирамиды, заключенная между этой плоскость и основанием, называется усеченной пирамидой. Сечение пирамиды также называется основанием усеченной пирамиды. 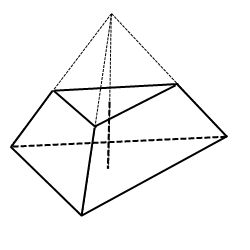 (по учеб. пособию «Геометрия 10-11» И. М. Смирнова)
| Прямая призма Призма, боковыми гранями которой являются прямоугольники, называется прямой. В противном случае призма называется наклонной. Прямая призма, основаниями которой являются правильные многоугольники, называется правильной. (по учеб. пособию «Геометрия 10-11» И. М. Смирнова)
|
| Пирамида Пирамида – многогранник, поверхность которого состоит из многоугольника, называемого основанием пирамиды, и треугольников имеющих общую вершину, называемых боковыми гранями пирамиды. Общая вершина боковых граней называется вершиной пирамиды. Ребра, сходящиеся в вершине пирамиды, называется боковыми ребрами. Определение: Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники и в каждой вершине сходятся одинаковое число граней. Наиболее простым правильным многогранником является треугольная пирамида, грани которой правильные треугольники. В каждой ее вершине сходится по три грани. Имея всего 4 грани, этот многогранник называется также тетраэдром, что в переводе с греческого языка означает «четырехгранник». !!!Теорема: Около любой треугольной пирамиды можно описать сферу, притом только одну. 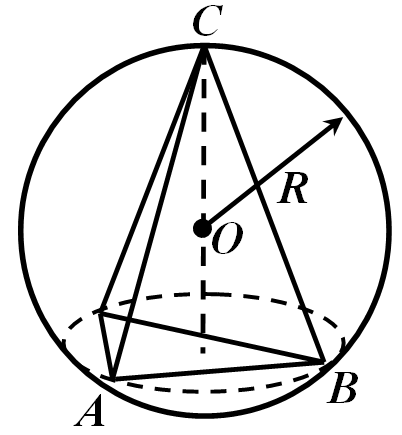 !!!Теорема: В любую треугольную пирамиду можно вписать сферу, и притом только одну. 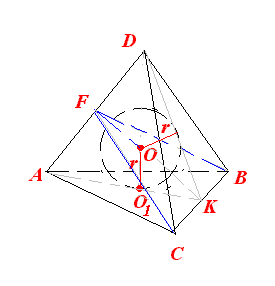 Объем пирамиды равен одной третьей произведения площади ее основания на высоту. (по учеб. пособию «Геометрия 10-11» И. М. Смирнова)
| Правильная пирамида Пирамида, в основании которой правильный многоугольник и все боковые ребра которой равны, называется правильной. (по учеб. пособию «Геометрия 10-11» И. М. Смирнова) Параллелепипед Параллелепипед – многогранник, поверхность которого состоит из шести параллелограммов. (по учеб. пособию «Геометрия 10-11» И. М. Смирнова)
Прямоугольный параллелепипед Параллелепипед, у которого все грани – прямоугольники, называется прямоугольным. (по учеб. пособию «Геометрия 10-11» И. М. Смирнова)
Параллелепипед Определение: Параллелепипед – это четырехугольная призма, основаниями которой являются параллелограммы. Причем за основание можно взять любую грань параллелепипеда. Диагональ параллелепипеда – это отрезок, соединяющий его противоположные вершины. Следствие. Параллелепипед имеет центр симметрии. Это – точка пересечения его диагоналей. Двенадцать ребер параллелепипеда образуют три четверки соответственно равных между собой и параллельных отрезков. ( по учеб. пособию «Геометрия 10-11» И. Ф. Шарыгина) Прямоугольный параллелепипед Теорема: ( теорема Пифагора для прямоугольного параллелепипеда). Пусть а, b и с – длины трех непараллельных ребер прямоугольного параллелепипеда, d – его диагональ. Тогда a2+ b2 + c2 = d2. ( Эта теорема представляет собой один из многих пространственных аналогов теоремы Пифагора.) ( по учеб. пособию «Геометрия 10-11» И. Ф. Шарыгина)
|
| Пирамида Определение: n-Угольной пирамидой называется многогранник, имеющий n+1 грань (т.е. Т+1-гранник), причем одна грань у него – n-угольник, а nоставшихся граней – треугольники с общей вершиной.
Особенность треугольной пирамиды состоит в том, сто любую грань можно рассматривать как основание. (три другие грани являются соответственно боковыми гранями.)
Теорема: (свойство пирамиды с равными боковыми ребрами). Если боковые ребра пирамиды равны между собой, то в основании этой пирамиды лежит многоугольник, около которого можно описать окружность. При этом вершина пирамиды проектируется в центр описанной около основания окружности. Теорема: (свойство пирамиды с равными углами между основанием и боковыми гранями). Если все углы между плоскостями боковых граней и плоскостью основания равны между собой ( иными словами, боковые грани наклонены к плоскости основания под равными углами), то все прямые, на которых лежат стороны основания, касаются одной окружности , а вершины пирамиды проектируются в центр этой окружности. Теорема: Сечением пирамиды плоскостью, параллельной основанию является многоугольник, подобный основанию. Определение: Пирамида называется правильной если в основании ее лежит правильный многоугольник, а все боковые ребра равны между собой. Правильным называется тетраэдр (т. е. треугольная пирамида), у которого все ребра равны между собой. Теорема: ( об описанной сфере треугольной пирамиды). Треугольная пирамида имеет единственную описанную сферу. Теорема ( о вписанной сфере треугольной пирамиды.) У любой треугольной пирамиды существует единственная вписанная сфера. | Теорема: (об отношении объемов треугольных пирамид). Рассмотрим три прямые, не лежащие в одной плоскости и проходящие через общую D. Пусть А1 и А2 – какие-то две точки на одной прямой, В1 и В2 – на другой, С1 и С2 – на третьей, V1 – объем тетраэдра (треугольной пирамиды) А1В1С1D, V2 - объем тетраэдра A2B2C2D. Тогда 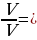 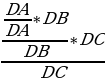 Теорема: ( вычисление объема тетраэдра, через площади двух граней, двугранный угол и ребро). Пусть P и Q – площади двух граней тетраэдра, а – длина общего ребра, 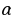 - величина двугранного угла между этими гранями. Тогда объем тетраэдра может быть вычислен по формуле V = - величина двугранного угла между этими гранями. Тогда объем тетраэдра может быть вычислен по формуле V = 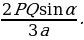 Теорема: ( вычисление объема тетраэдра через два противоположных ребра, расстояние и угол между ними.) Пусть а и b – длины двух противоположных ребер тетраэдра, d – расстояние, 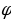 – угол между ними. Тогда объем тетраэдра может быть найден по формуле V = – угол между ними. Тогда объем тетраэдра может быть найден по формуле V = 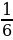 abd abd 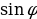 . . ( по учеб. пособию «Геометрия 10-11» И. Ф. Шарыгина) |








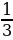 SH.
SH.

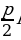


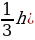 1 +
1 + 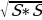 1)
1) 

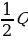 d. ( по учеб. пособию «Геометрия 10-11» И. Ф. Шарыгина)
d. ( по учеб. пособию «Геометрия 10-11» И. Ф. Шарыгина)


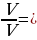
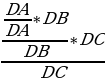
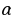 - величина двугранного угла между этими гранями. Тогда объем тетраэдра может быть вычислен по формуле V =
- величина двугранного угла между этими гранями. Тогда объем тетраэдра может быть вычислен по формуле V = 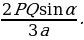
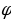 – угол между ними. Тогда объем тетраэдра может быть найден по формуле V =
– угол между ними. Тогда объем тетраэдра может быть найден по формуле V = 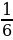 abd
abd 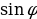 .
.















