Методическая разработка "Теоремы в геометрии"

Л.С. Атанасян. Геометрия 10-11

c

b

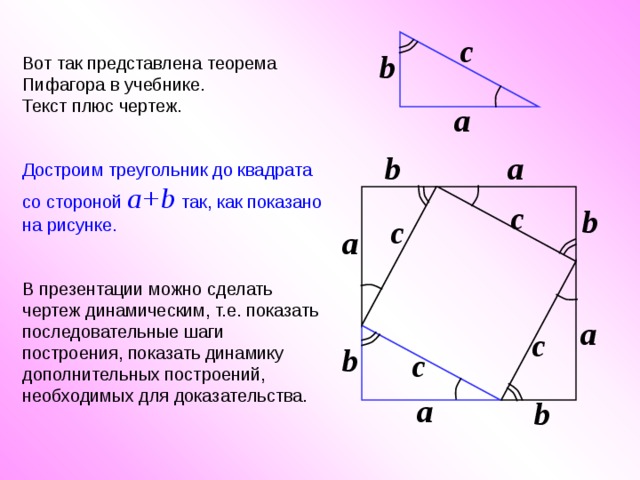
Вот так представлена теорема Пифагора в учебнике.

Текст плюс чертеж.

Достроим треугольник до квадрата со стороной a+b так, как показано на рисунке.

В презентации можно сделать чертеж динамическим, т.е. показать последовательные шаги построения, показать динамику дополнительных построений, необходимых для доказательства.

a

b

a

c

b

c

a

a

c

b

c

a

b

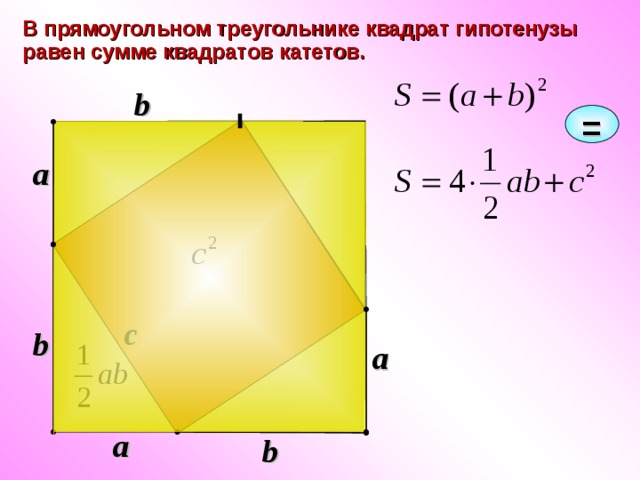
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

b

=

a

c

b

a

a

b

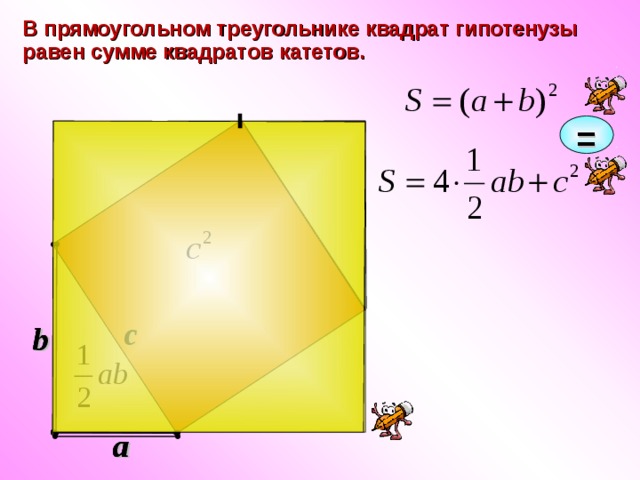
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

=

c

b

b

b

a

a

a

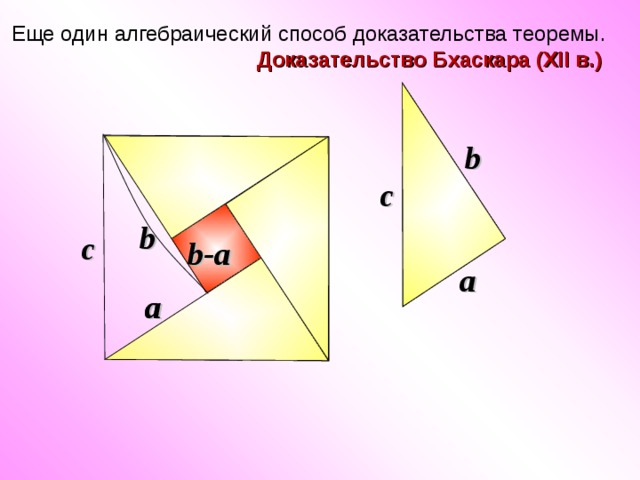
Еще один алгебраический способ доказательства теоремы.

Доказательство Бхаскара (XII в.)

b

c

b

c

b-a

a

a

a

(b-a) 2 +4*1/2ab=c 2

5

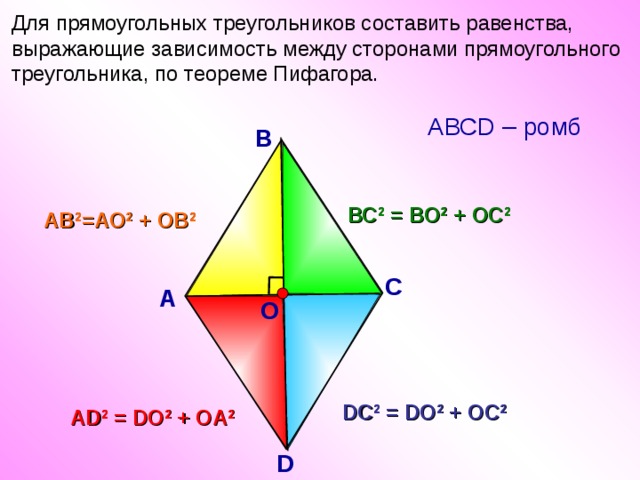
Для прямоугольных треугольников составить равенства, выражающие зависимость между сторонами прямоугольного треугольника, по теореме Пифагора.

АВСD – ромб

В

ВС 2 = ВО 2 + ОС 2

АВ 2 =АО 2 + ОВ 2

О

С

А

DC 2 = DO 2 + OC 2

АD 2 = DO 2 + OA 2

D

6

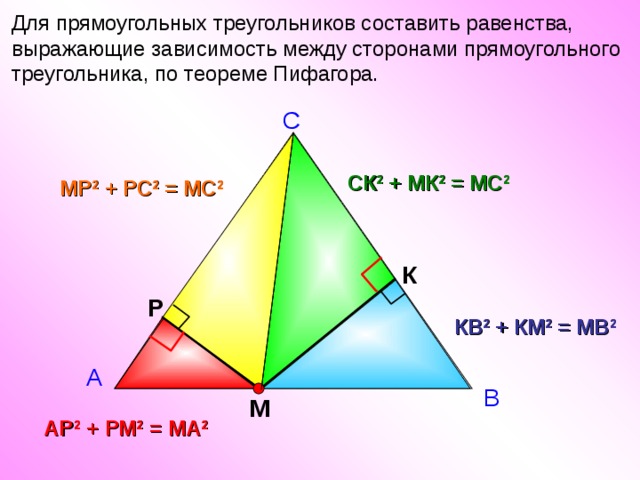
Для прямоугольных треугольников составить равенства, выражающие зависимость между сторонами прямоугольного треугольника, по теореме Пифагора.

С

СК 2 + МК 2 = МС 2

МР 2 + РС 2 = МС 2

К

Р

КВ 2 + КМ 2 = МВ 2

А

В

М

АР 2 + РМ 2 = МА 2

6

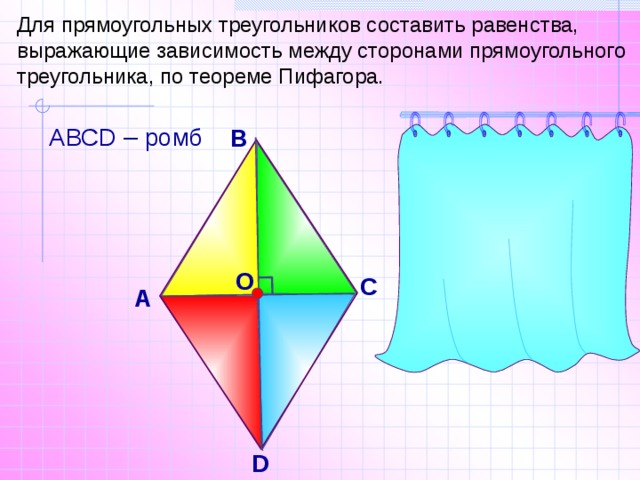
Для прямоугольных треугольников составить равенства, выражающие зависимость между сторонами прямоугольного треугольника, по теореме Пифагора.

АВСD – ромб

В

АВ 2 =АО 2 + ОВ 2

DC 2 = DO 2 + OC 2

АD 2 = DO 2 + OA 2

О

С

А

ВС 2 = ВО 2 + ОС 2

D

8

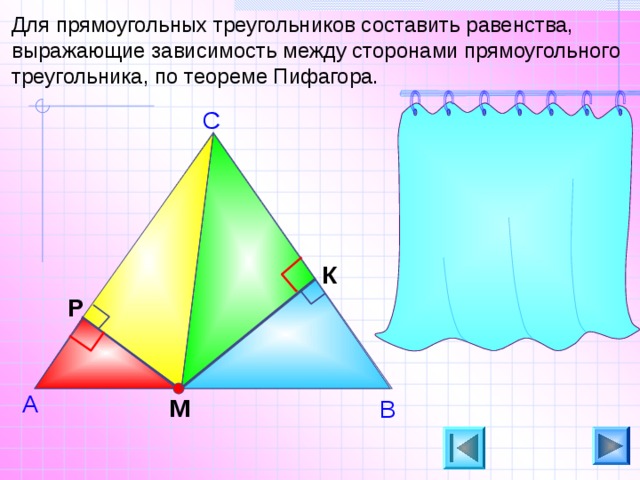
Для прямоугольных треугольников составить равенства, выражающие зависимость между сторонами прямоугольного треугольника, по теореме Пифагора.

С

МР 2 + РС 2 = МС 2

КВ 2 + КМ 2 = МВ 2

АР 2 + РМ 2 = МА 2

К

СК 2 + МК 2 = МС 2

Р

А

М

В

9

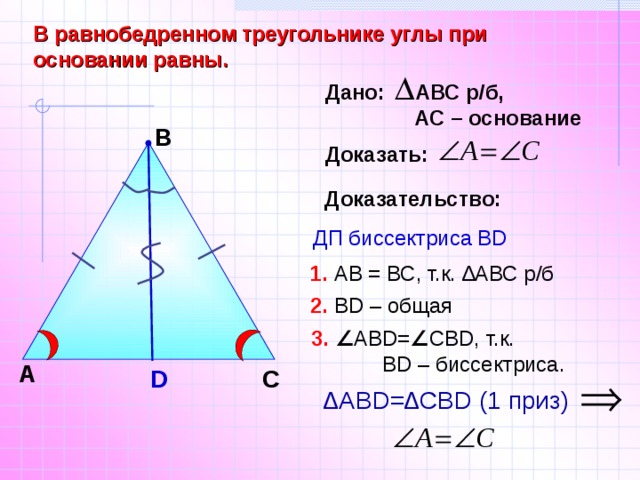
В равнобедренном треугольнике углы при основании равны.

Дано: АВС р/б,

АС – основание

В

Доказать:

Доказательство:

ДП биссектриса ВD

1. АВ = ВС, т.к. ∆АВС р/б

2. ВD – общая

3. ∠ ABD= ∠ СВD, т.к.

ВD – биссектриса.

А

D

С

∆ АВD=∆СBD (1 приз)

III признак равенства треугольников

по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника,

то такие треугольники равны.

У

С

Л

О

В

И

Е

З А К Л Ю Ч Е Н И Е

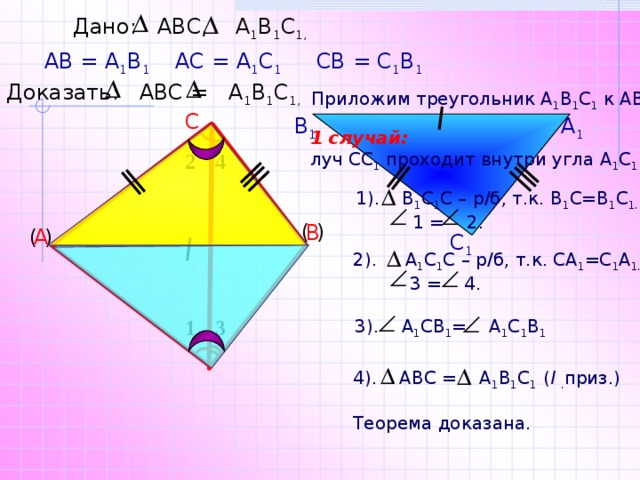
Дано: АВС, А 1 В 1 С 1,

АВ = А 1 В 1

АС = А 1 С 1

СВ = С 1 В 1

Доказать: АВС = А 1 В 1 С 1,

Приложим треугольник А 1 В 1 С 1 к АВС.

С

В 1

А 1

1 случай:

луч СС 1 проходит внутри угла А 1 С 1 В 1 .

2

4

1). В 1 С 1 С – р/б, т.к. В 1 С=В 1 С 1.

1 = 2.

( )

В

( )

А

С 1

2). А 1 С 1 С – р/б, т.к. СА 1 =С 1 А 1.

3 = 4.

1

3

3). А 1 СВ 1 = А 1 С 1 В 1

4). АВС = А 1 В 1 С 1 ( I . приз.)

Теорема доказана.

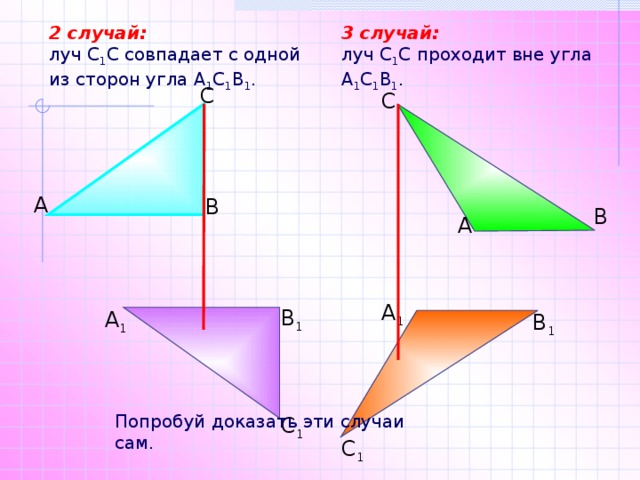
2 случай:

3 случай:

луч С 1 С проходит вне угла А 1 С 1 В 1 .

луч С 1 С совпадает с одной из сторон угла А 1 С 1 В 1 .

С

С

А

В

В

А

А 1

В 1

А 1

В 1

Попробуй доказать эти случаи сам.

С 1

С 1

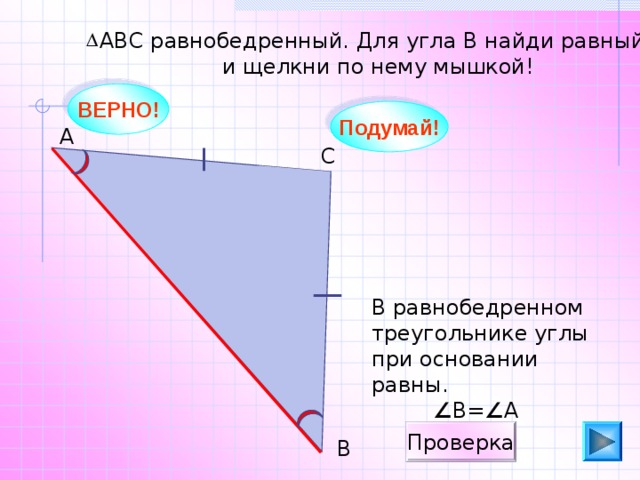
АВС равнобедренный. Для угла В найди равный

и щелкни по нему мышкой!

ВЕРНО!

Подумай!

А

С

В равнобедренном треугольнике углы при основании равны.

∠ В= ∠ А

Пригласите к компьютеру ученика.

Проверка

В

13

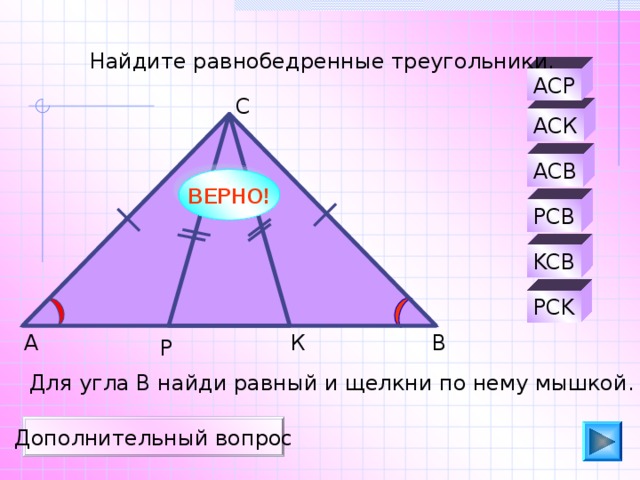
Найдите равнобедренные треугольники.

АСР

С

АСК

АСВ

ВЕРНО!

PCB

KCB

PCK

Пригласите к компьютеру ученика.

К

А

В

Р

Для угла В найди равный и щелкни по нему мышкой.

Дополнительный вопрос

13

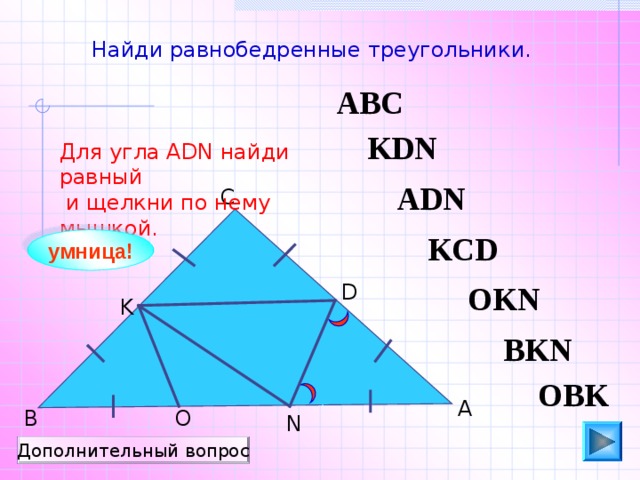
Найди равнобедренные треугольники.

ABC

KDN

Для угла АDN найди равный

и щелкни по нему мышкой.

ADN

С

KCD

умница!

OKN

D

K

Пригласите к компьютеру ученика.

BKN

OBK

А

В

O

N

Дополнительный вопрос

13

23см

23см

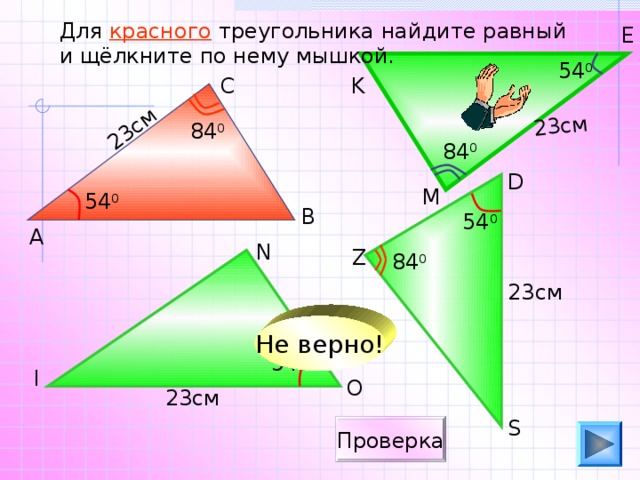
Для красного треугольника найдите равный

и щёлкните по нему мышкой.

E

54 0

K

C

84 0

84 0

D

M

54 0

B

54 0

А

N

Z

84 0

23см

Не верно!

54 0

I

O

23см

S

Проверка

13

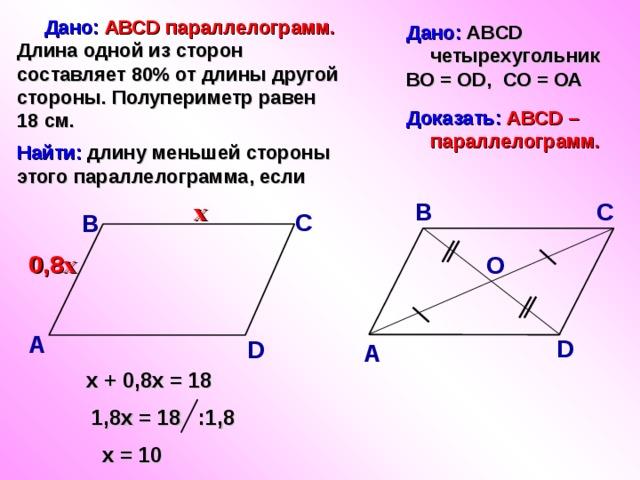
Дано: АВСD параллелограмм. Длина одной из сторон составляет 80% от длины другой стороны. Полупериметр равен 18 см.

Найти: длину меньшей стороны этого параллелограмма, если

Дано: ABCD четырехугольник

ВО = ОD, СО = ОА

Доказать: АВСD –параллелограмм.

х

В

С

С

В

0,8 х

О

Л.И. Звавич, Е.В. Потоскуев «Тестовые задания по геометрии» 8 класс.

А

D

D

А

х + 0,8х = 18

1,8х = 18

:1,8

х = 10

18

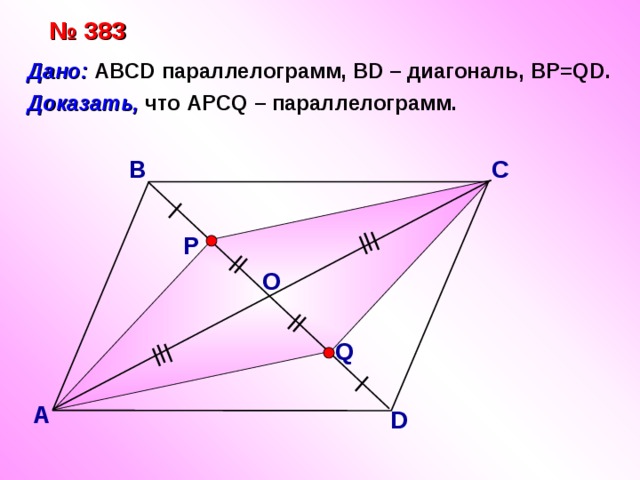
№ 383

Дано: ABCD параллелограмм, BD – диагональ, BP=QD.

Доказать, что АPCQ – параллелограмм.

В

С

Р

О

Q

А

D

19

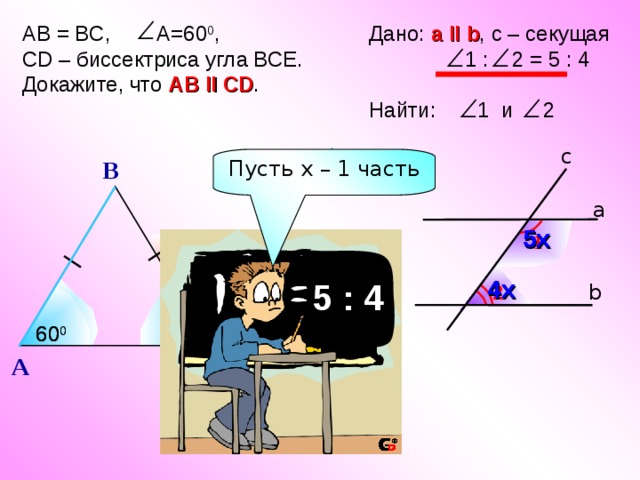
биссектриса

Дано: а II b , с – секущая

1 : 2 = 5 : 4

Найти: 1 и 2

AB = BC, A=60 0 ,

CD – биссектриса угла ВСЕ.

Докажите, что АВ II CD .

c

Пусть х – 1 часть

B

D

а

5х

1

4х

5 : 4

b

2

120 0

60 0

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

60 0

60 0

60 0

E

С

A

20

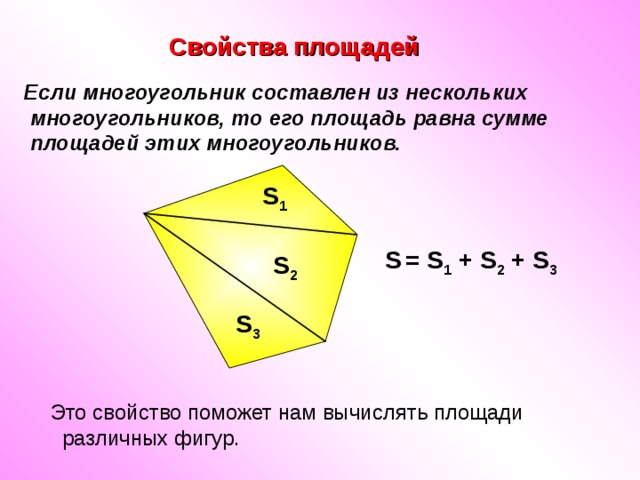
Свойства площадей

Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

S 1

S = S 1 + S 2 + S 3

S 2

S 3

Это свойство поможет нам вычислять площади различных фигур.

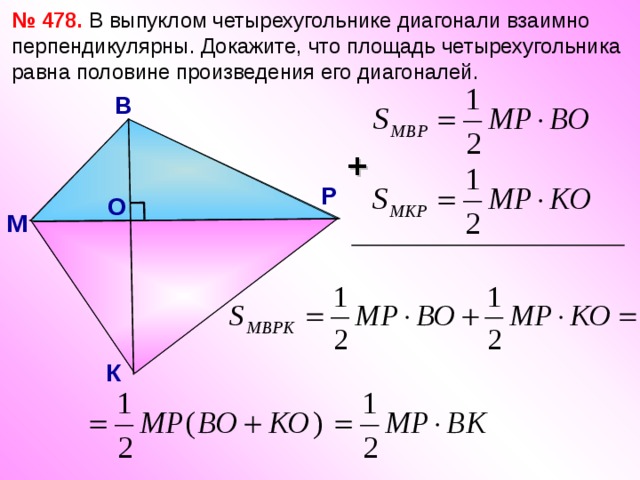
№ 478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырехугольника равна половине произведения его диагоналей.

В

+

Р

О

М

Л.С. Атанасян «Геометрия 7-9» № 478.

К

22

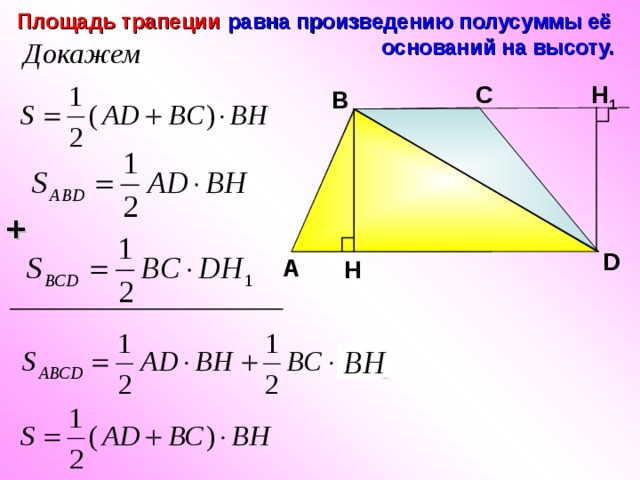
Площадь трапеции равна произведению полусуммы её

оснований на высоту.

H 1

С

В

+

D

А

H

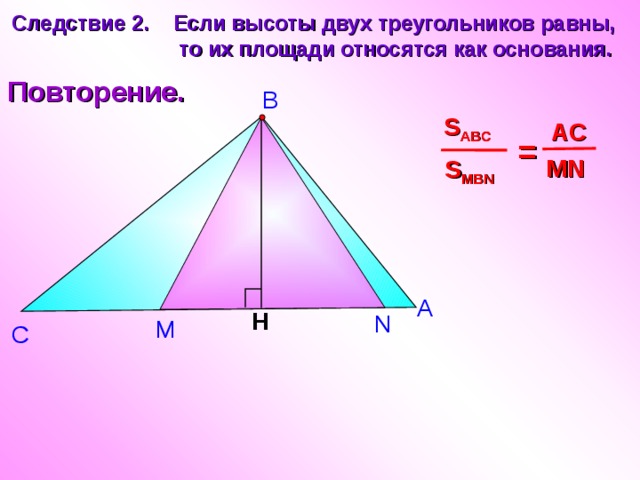
Следствие 2. Если высоты двух треугольников равны,

то их площади относятся как основания.

Повторение.

В

S ABC

AC

=

MN

S MBN

А

H

N

Повторение.

М

С

24

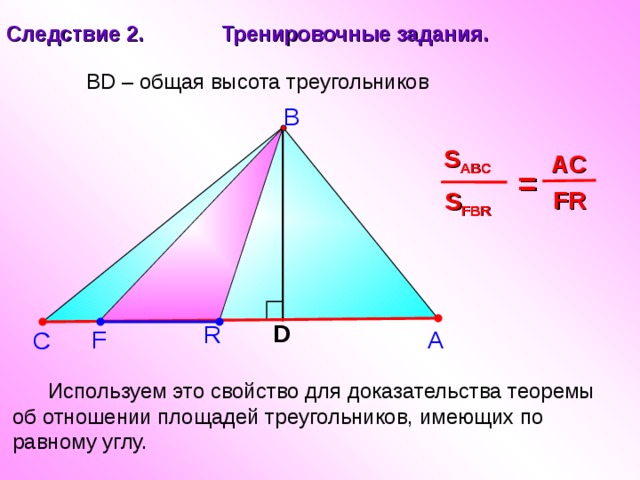
Следствие 2. Тренировочные задания.

BD – общая высота треугольников

В

S ABC

AC

=

FR

S FBR

D

R

А

F

С

Используем это свойство для доказательства теоремы об отношении площадей треугольников, имеющих по равному углу.

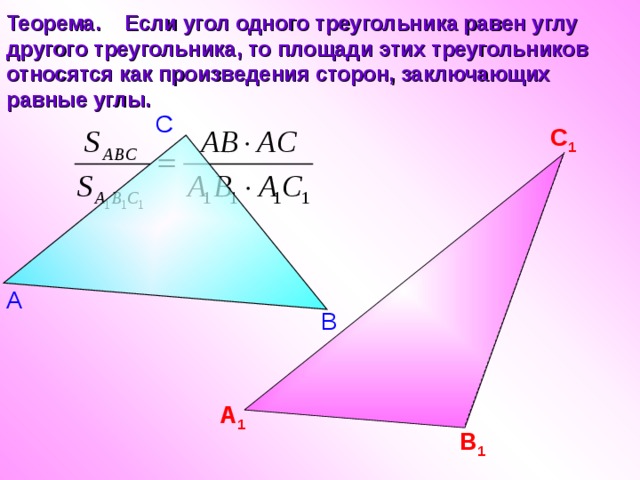
Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

С

С 1

А

В

А 1

В 1

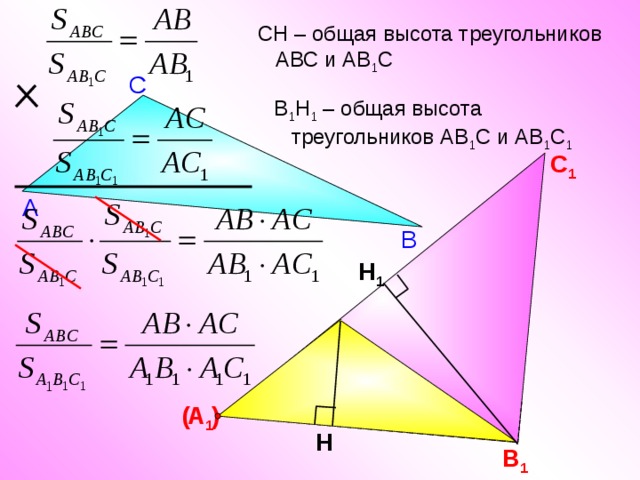
СН – общая высота треугольников АВС и АВ 1 С

С

В 1 Н 1 – общая высота треугольников АВ 1 С и АВ 1 С 1

С 1

А

В

Н 1

1

А 1

( )

Н

В 1

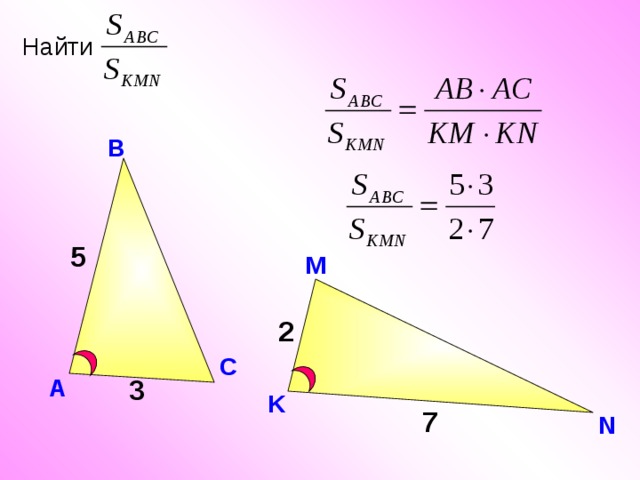
Найти

В

5

M

Н.Ф. Гаврилова «Поурочные разработки по геометрии: 8 класс»

2

С

3

А

K

7

N

27

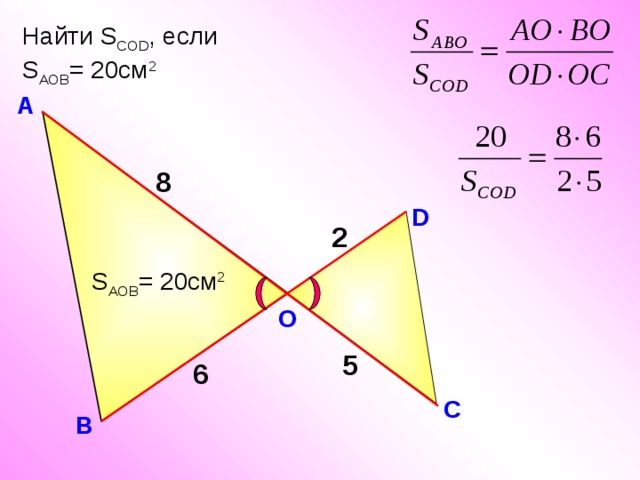
Найти S COD , если S AOB = 20см 2

А

8

D

2

S AOB = 20см 2

O

Н.Ф. Гаврилова «Поурочные разработки по геометрии: 8 класс»

5

6

С

В

29

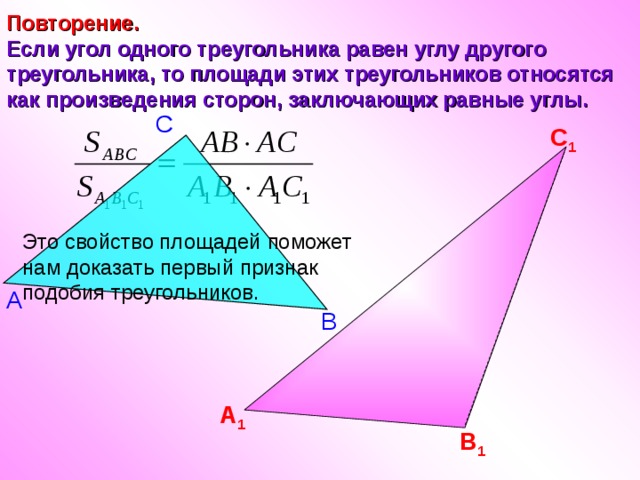
Повторение.

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

С

С 1

Это свойство площадей поможет нам доказать первый признак подобия треугольников.

А

В

А 1

В 1

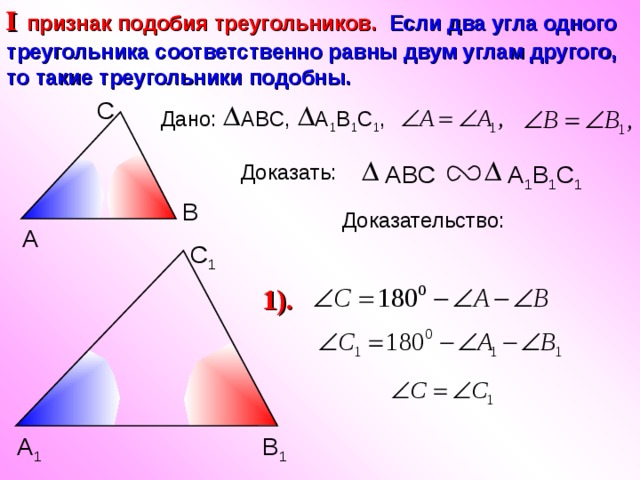
I признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

С

А 1 В 1 С 1 ,

ABC,

Дано:

Доказать:

А 1 В 1 С 1

ABC

В

Доказательство:

А

С 1

1).

А 1

В 1

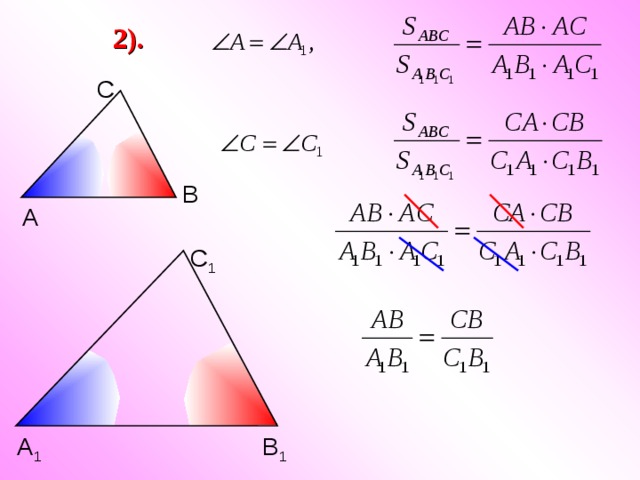
2).

С

В

А

С 1

В 1

А 1

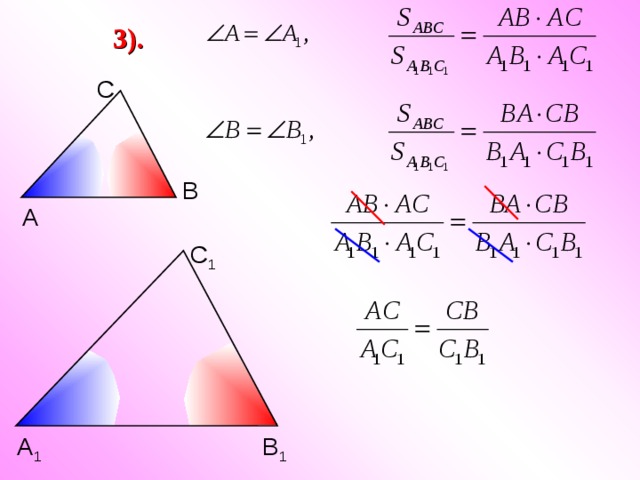
3).

С

В

А

С 1

В 1

А 1

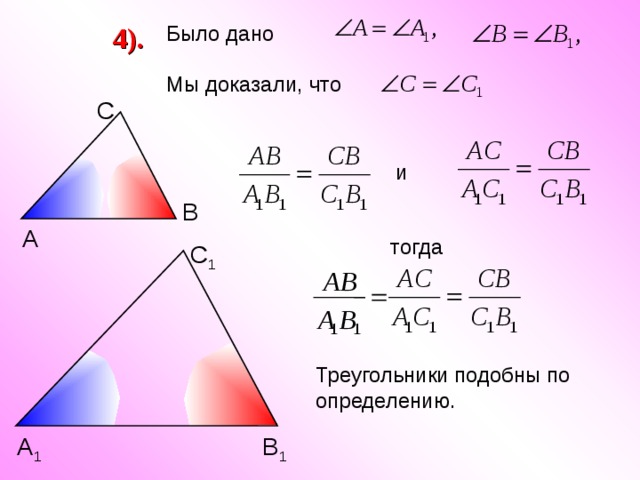
4).

Было дано

Мы доказали, что

С

и

В

А

тогда

С 1

AB



B

A

1

1

Треугольники подобны по определению.

В 1

А 1