Методическая разработка. "Подготовка к олимпиадам по математике.Тренировочные задания для 9, 10 класса"

Задания для 10 класса.

Отличные от нуля числа a, b подобраны так, что уравнение не имеет решений. Докажите, что числа a и b совпадают по модулю.

Расставьте по кругу числа 1, 2, 3, .., 9 так, чтобы среди любых трёх чисел, записанных подряд, одно было равно полусумме двух других.

Четыре круга попарно касаются друг друга внешним образом так, что точки касания образуют квадрат. Следует ли отсюда, что все круги имеют одинаковые радиусы?

Какое наименьшее число клеток можно отметить на шахматной доске так, чтобы в каждом прямоугольнике из 9 или более клеток хотя бы одна клетка была отмечена? Нарисуйте соответствующий рисунок и объясните, почему отметить меньшее число клеток с соблюдением условия невозможно.

В главном супермаркете страны рыцарей и лжецов продаются блюдца и чашки. Чашки бывают белые, синие, и красные, а блюдца – белые, желтые, красные и зеленые. Во время рождественской распродажи 11 человек купили по чайному сервизу (блюдце и чашка, возможно, разного цвета). При выходе каждый получил анкету, состоящую из трёх вопросов: "Вы купили желтую чашку?", "Вы купили белое блюдце?", "Вы купили желтое блюдце?". На каждый вопрос утвердительно ответили по три человека. Докажите, что какие-то двое покупателей купили одинаковые сервизы.

Расположите на плоскости четыре точки так, чтобы попарные расстояния между ними составляли 5, 5, 5, 6, 8, 10 см.

Сколько существует различных натуральных чисел n от 1 до 100, для которых число n является точным квадратом?

Можно ли подобрать три различных числа, образующие арифметическую прогрессию, так, чтобы их попарные произведения тоже составляли арифметическую прогрессию?

На оси ординат координатной плоскости выбраны точки А и В, причём точка В лежит выше начала координат, а точка А ниже начала координат. Пусть Р – произвольная точка окружности, построенной на отрезке АВ как на диаметре, а М – точка пересечения отрезка АР с осью абсцисс. Докажите, что углы ВОР и ВМР равны (О - начало координат).

На столе в ряд выложены 2n карточек, на каждой из которых написано некоторое число. При этом все написанные числа различны. Петя и Вася по очереди забирают любую из двух крайних карточек, причём Петя берёт первым. Докажите, что Петя всегда сможет так выбирать карточки, что сумма чисел на выбранных им карточках не меньше, чем сумма чисел на карточках, выбранных Васей.

РЕШЕНИЯ ЗАДАЧ

10 класс

Числитель обращается в 0 при . Чтобы это значение неизвестного не было решением уравнения, оно должно обращать в 0 и знаменатель. Это приводит к равенству a²–b²=0, следовательно a = b .

Например, так: 9, 5, 1, 3, 2, 4, 6, 8, 7.

Ответ. Не обязательно. Решение. Например, построим ромб O₁O₂O₃O₄ с углом 60⁰ и стороной 1+√3. На сторонах ромба построим точки А, В, С и D так, что O₁A=O₁D=O₃B=O₃C=1. Длины сторон четырехугольника ABCD равны √3, а все углы прямые. Если провести окружности с центрами в точках O₁ и O₃ радиуса 1, а также окружности с центрами в точках O₂ и O₄ радиуса √3, то точки А, В, С и D будут точками касания для этих окружностей.

Ответ. 7 клеток. Решение. Пример для 7 клеток – на левом рисунке. Если отмечено не более 6 клеток, то, выделив 6 прямоугольников как на среднем рисунке, видим, что должно быть отмечено по клетке в каждом прямоугольнике, поэтому оставшиеся клетки с нулями не отмечены. Аналогично, разбиение на правом рисунке дает нам еще 6 неотмеченных клеток (с нулями), и закрашенный прямоугольник состоит из 10 неотмеченных клеток.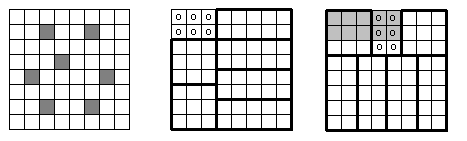

Достаточно доказать, что, по крайней мере, четыре покупателя купили блюдца одного цвета. Прежде всего, заметим, что среди посетителей ровно три лжеца, поскольку трое сказали, что купили несуществующие желтые чашки. Рассмотрим два случая. Первый: хотя бы один лжец купил красное или зеленое блюдце. Тогда каждый из них дал утвердительный ответ на последние два вопроса. Но каждый покупатель жёлтого или белого блюдца (неважно, лжец или рыцарь) даст утвердительный ответ на один из этих вопросов. А, поскольку всего прозвучало 6 утвердительных ответов на эти вопросы, на самом деле белое или жёлтое блюдце купили не более четырёх человек. Значит, красное или зелёное блюдце купили не менее семи человек. Тогда хотя бы одно из блюдец этого цвета купили не менее четырёх человек. Теперь второй случай: все лжецы купили желтые или белые блюдца. Можно считать, что не менее двух лжецов купили жёлтые блюдца. Тогда на последнюю фразу утвердительно ответит не более одного лжеца и, соответственно не менее двух рыцарей. Снова нашли четверых покупателей жёлтых блюдец.

Решение. Например: три точки располагаем в вершинах прямоугольника со сторонами 6 и 8 см, а четвертую – в точке пересечения его диагоналей.

7.Ответ: 55. Решение. Число nn является точным квадратом при всех чётных n=2k. В самом деле: (2k)2k=(2kkk)2. Пусть n=2k+1 –-нечётное и (2k+1)2k+1=х2 . Тогда . Это равенство показывает, что число (2k+1)2k+1 является квадратом в том и только том случае, когда число 2k+1 является квадратом. Значит, ко всем чётным числам надо добавить все квадраты нечётных чисел, не превосходящие числа 100. От 1 до 100 имеем 50 четных чисел и 5 нечетных точных квадратов (1, 9, 25, 49, 81). Итого 55 чисел.

8.Ответ: да, можно. Решение. Например: -2, 1, 4. Их попарные произведения: -8, -2, 4. Примечание. Как можно найти эти числа? Например, так. Обозначим искомые числа a, b, c. В силу свойств арифметической прогрессии одно из этих чисел есть среднее арифметическое других. Пусть b=(a+c)/2 . Тогда тройка попарных произведений: ab, ac, bc. Будем требовать выполнения следующего условия аb=(aс+bc)/2 . Выразим, например, а из первого равенства и подставим во второе. В результате приходим к соотношениям a = -2b, c=4b.

9. Решение. Рассмотрим четырехугольник ОВРМ. В нем ВРМ = 90˚ (вписанный, опирающийся на диаметр), ВОМ = 90˚. Таким образом, ВРМ + ВОМ = 180˚. Значит, около четырехугольника ОВРМ можно описать окружность. Для этой окружности углы ВОР и ВМР равны как вписанные, опирающиеся на одну дугу.

10. Решение. Найдем сумму чисел, написанных на карточках, расположенных в ряду на нечетных местах. Аналогично найдем сумму чисел, написанных на карточках с четными номерами. Пусть, например, первая сумма не меньше второй. Докажем, что Петя может забрать себе все карточки с нечетными номерами. Первым ходом он берет себе карточку под номером 1, тогда перед ходом Васи имеем ряд, который начинается с четного номера и заканчивается четным номером. Независимо от того, какую карточку выбирает Вася, перед ходом Пети ряд будет начинаться или заканчиваться карточкой под нечетным номером. Петя берет именно её и т.д. Если Петя будет действовать таким образом, то после каждого хода Васи на каждом из концов будет находиться карточка с чётным номером. Это означает, что Петя сможет довести свою стратегию до конца и собрать не меньшую сумму.

Задания для 9 класса.

Какое число больше А= или В=?

У 6 девятиклассников есть 5 одинаковых булок. Они хотят разделить булки между собой поровну таким образом, чтобы каждая булка была разрезана на равные куски (при этом разные булки могут быть разрезаны на разное число кусков) и всего получилось 12 кусков. Как им это сделать?

Прямоугольник со сторонами 5 см и 8 см симметрично перегнули по пунктирным линиям так, что обе верхние вершины попали в одну точку. Найдите площадь полученной трапеции.

Докажите, что существует три последовательных 1000-значных натуральных числа, каждое из которых делится на произведение всех своих цифр.

Плоскость выкрашена в 2 цвета: синий и красный. При этом имеются и точки синего цвета, и точки красного цвета. Докажите, что найдётся параллелограмм, у которого три вершины одного цвета, а четвёртая вершина другого цвета.

Натуральные числа х и у подобраны так, что ху+1 – точный квадрат. Докажите, что можно подобрать отличное от х и у натуральное число а такое, что каждое из чисел ах+1 и ау+1 тоже будет точным квадратом.

Автомобилисты Иванов, Петров и Сидоров одновременно с разными скоростями выехали на трассу, ведущую из пункта А в пункт В. В тот момент, когда Иванов проехал всю трассу, Петров находился посередине между ним и Сидоровым. Если Сидоров будет ехать со скоростью, вдвое большей, то уже он будет посередине между Ивановым и Петровым в тот момент, когда Иванов проедет всю трассу. Как и во сколько раз должен изменить свою скорость Иванов, чтобы оказаться посередине между Петровым и Сидоровым в момент, когда самый быстрый гонщик проедет всю трассу?

Во вписанном четырехугольнике есть пара углов, сумма которых вдвое больше суммы остальных углов, и есть пара углов, сумма которых втрое больше суммы оставшихся углов. Найдите все углы четырехугольника.

В выпуклом четырёхугольнике ABCD диагональ AC делит пополам отрезок, соединяющий середины сторон AD и BC. Докажите, что диагональ AC делит пополам диагональ BD.

В тридевятом царстве 100 городов, каждый из которых занумерован числами от 1 до 100. Царь Горох отдал приказ соединить некоторые из городов беспосадочными авиационными рейсами так, чтобы выполнялось следующее условие. Два города соединены беспосадочным рейсом с одним и тем же третьим городом в тех и только тех случаях, когда номер одного из этих двух городов делится на номер другого. Можно ли выполнить приказ царя?

Девятый класс

решения задач

Ответ: AB.

Решение. Возведём оба числа в квадрат: А²=; В²=. Отсюда видно, что А²B² и, в силу положительности А и В, AB.

Ответ. Например, так. Разрезать три булки на 2 половинки каждую, а 2 другие булки на 3 трети каждую. Получается шесть половинок и шесть третьих частей. Каждому девятикласснику нужно дать по одной половинке и одной третьей части.

Ответ: 27,5 см².

Решение. Пусть АВСD – исходный прямоугольник, АКМD – полученная трапеция, О – точка касания двух согнутых половинок. Проведём через точку О высоту трапеции так, что точка Т лежит на нижнем, а точка S на верхнем основании. Тогда АТ=4 и по теореме Пифагора ОТ=3, OS=2. Осталось найти верхнее основание трапеции КМ. Пусть КS=х. Тогда КО=КВ=4–x. Теорема Пифагора для прямоугольного треугольника KOS даёт уравнение (4–х)²=х²+4. Отсюда х=1,5, КМ=3 и площадь трапеции равна =27,5.

Решение. Например, годятся следующие числа: 11..11, 11..12, 11..13. Здесь в первом числе 1000 единиц, во втором и третьем по 999 единиц. Легко видеть, что сумма цифр третьего числа равна 999+3. Поэтому это число делится на 3. Всё остальное очевидно.

Решение. Возьмём две точки разного цвета. Пусть точка А – красная, точка В – синяя, а середина М отрезка АВ, например, красная (если она синяя, то рассуждения проводятся аналогично) Рассмотрим произвольный отрезок КР, равный и параллельный отрезку АМ (и, соответственно, ВМ). Если оба конца этого отрезка красные или оба синие, то годится параллелограмм со сторонами ВМ и КР. Если один из концов красный, а другой синий, то – параллелограмм со сторонами АМ и КР.

Решение. Если ху+1=с², то можно взять а=х+у+2с. Тогда хa+1=aу+1=x² + xy + 2cx +1= x² +2cx+с²=(x+c)². Примечание. Попытаемся подобрать число а. Для этого запишем равенство хa+1= b². Вычитая из этого равенства исходное, получаем: x(a–y)=(b–c)(b+c). Достаточно добиться выполнения равенств x=b–c, a–y=b+c. Вычитая из второго равенства первое, находим число а.

Ответ: уменьшить в 1,75 раза. Решение. Пусть И, П и С (единиц в час) – скорости Иванова, Петрова и Сидорова соответственно. Чтобы Петров оказался между Ивановым и Сидоровым в момент, когда Иванов проедет всю трассу, скорость Петрова должна составить среднее арифметическое скоростей Иванова и Сидорова, то есть 2П = И + С. Аналогично, 2С – среднее арифметическое И и П, 4С =И + П. Выразим остальные скорости через И:

С = 2П – И, 8П – 4И = И + П, откуда П = 5/7 И, С = 3/7 И. Чтобы Иванов оказался между Петровым и Сидоровым в момент, когда Петров проедет всю трассу, его скорость должна составить среднее арифметическое скоростей Петрова и Сидорова, то есть 4/7 И. Чтобы скорость Иванова стала 4/7 И, он должен исходную скорость уменьшить в 7 /4 раза, или в 1,75 раза.

Возможны другие решения. Например, можно было учитывать не среднее арифметическое, а длину трассы. Или учитывать не скорости, а время преодоления трассы.

8. Ответ: 105, 165, 75 и 15 градусов. Решение. Из условия следует, что в четырёхугольнике есть пара углов, составляющих в сумме 120 градусов и пара углов, составляющих в сумме 90 градусов. В эти пары входит один угол, т.к в противном случае сумма всех углов четырёхугольника составляла бы 210 градусов. Это позволяет считать, что ÐА +ÐB = 120° и ÐВ +ÐC = 90°, откуда ÐA–ÐC = 30°. Но по свойству вписанного четырехугольника ÐC+ÐА = 180°, значит ÐА = 105°, ÐC = 75°, ÐВ = 15°. Наконец, ÐD=165°.

9. Решение. Пусть М и К – середины сторон AD и BC, Т – точка пересечения АС и KМ. По условию, Т – середина МК. Пусть Р – середина AB, Е – точка пересечения МР и АС, Н – точка пересечения диагоналей. Нам нужно доказать, что Н – середина диагонали BD. Так как РК – средняя линия треугольника АВС, РК параллельна АС. Тогда ЕТ в треугольнике МРК проходит через середину стороны МК параллельно РК, ЕТ является средней линией треугольника. Тогда Е – середина МР. МР – средняя линия треугольника АBD, PE и EМ – средние линии треугольников АНD и АНВ соответственно. Поэтому НD в два раза больше, чем МЕ, и НВ в 2 раза больше, чем ЕВ. Но тогда BН = НD = МР, Н – середина отрезка BD, что и требовалось доказать.

10. Ответ: нельзя. Решение. Если бы мы могли выполнить требования, то города с номерами 1 и 97 соединены с одним и тем же городом. Пусть этот город A занумерован числом a. Город А и город с номером 1 должны быть соединены с одним и тем же городом. Этот город имеет общего соседа с городом, занумерованным числом 97, поэтому его номер b либо делится на 97, либо является делителем числа 97. Но все делители 1 и 97 простого числа 97 заняты, а следующее число 194, делящееся на 97, уже больше ста. Возможны решения, основанные на рассмотрении не числа 97, а других чисел.