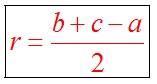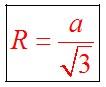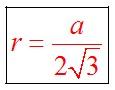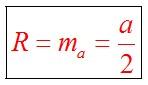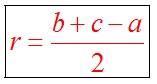Методическое пособие 8 класс "Окружность"

Окружность

8 класс

Свойства биссектрисы треугольника

ОПРЕДЕЛЕНИЕ

Биссектриса угла треугольника – это луч, который исходит из вершины треугольника и делит данный угол пополам.

ОПРЕДЕЛЕНИЕ

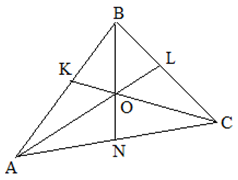
Три биссектрисы треугольника пересекаются в одной точке, которая называется инцентром треугольника.

ОПРЕДЕЛЕНИЕ

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой, находящейся на противолежащей стороне.

Свойства биссектрисы угла треугольника

1. Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам:

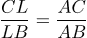
1. Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник.

2. Биссектриса угла – это геометрическое место точек, равноудаленных от сторон этого угла.

3. Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.

4. В правильном треугольнике биссектриса является медианой и высотой.

Свойства медианы треугольника

ОПРЕДЕЛЕНИЕ

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

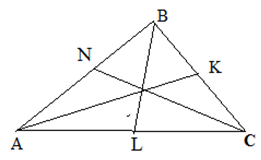
Свойства медиан треугольника

1. Медиана разбивает треугольник на два равновеликих треугольника (т.е. на треугольники с одинаковой площадью).

2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, начиная от вершины. Эта точка называется центром тяжести треугольника.

3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

4. В равнобедренном треугольнике медиана, опущенная на основание, является биссектрисой и высотой.

5. В равностороннем треугольнике любая медиана является высотой и биссектрисой.

Свойства высоты треугольника

ОПРЕДЕЛЕНИЕ

Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение.

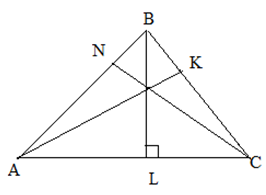
Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.

Свойства высоты треугольника

1. В остроугольном треугольнике высоты пересекаются внутри треугольника; в тупоугольном – вне треугольника; в прямоугольном – в вершине прямого угла.

2. В прямоугольном треугольнике катеты являются высотами.

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

4. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

5. В равнобедренном треугольнике высота, опущенная на основание, является медианой и биссектрисой.

6. В равностороннем треугольнике все высоты являются медианами и биссектрисами.

Серединный перпендикуляр треугольника

Определение и формулы для расчета серединного перпендикуляра треугольника

ОПРЕДЕЛЕНИЕ

Серединный перпендикуляр треугольника – это перпендикуляр, проведенный к середине стороны треугольника.

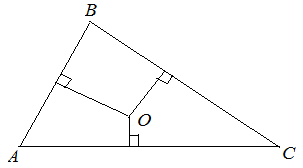
Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанной окружности.

Точка пересечения серединных перпендикуляров в остроугольном треугольнике лежит внутри треугольника; в тупоугольном – вне треугольника; в прямоугольном – на середине гипотенузы.

Свойства срединных перпендикуляров треугольника:

• Любая точка серединного перпендикуляра к стороне равноудалена от концов этой стороны.

• Любая точка, равноудаленная от концов стороны, лежит на серединном перпендикуляре к ней.

• Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Свойства касательной, секущей и хорды

ОПРЕДЕЛЕНИЕ

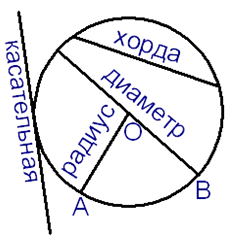
Окружностью называется геометрическое место точек, равноудаленных от одной точки, которая называется центром окружности.

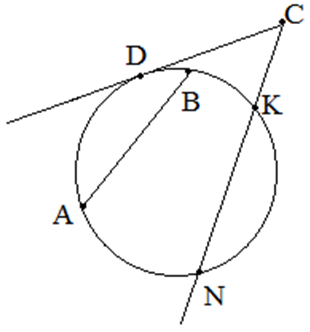
Отрезок, соединяющий две точки окружности, называется хордой (на рисунке это отрезок AB). Хорда, проходящая через центр окружности, называется диаметром окружности.

Хорда окружности обладает следующими свойствами

1. Хорды, находящиеся на одинаковом расстоянии от центра окружности, равны.

2. Если хорды стягивают равные центральные углы, то они равны.

3. Если диаметр перпендикулярен хорде, то он проходит через ее середину.

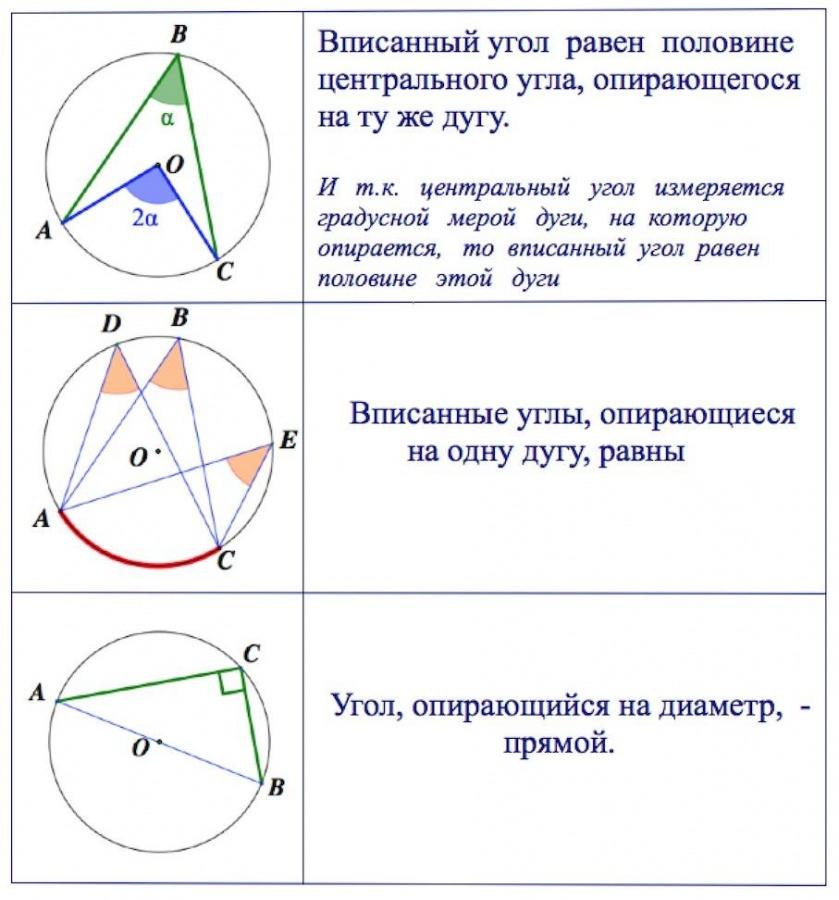
4. Если вписанные углы опираются на одну хорду, то они равны.

5. Две дуги равны, если они заключены между двумя равными хордами.

6. Если пара вписанных углов опирается на одну и ту же хорду, а их вершины лежат по разные стороны хорды, то их сумма составляет 180°.

7. Для любых двух хорд AB и CD, пересекающихся в точке О, выполняется равенство: .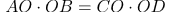

Прямая, имеющая с окружностью одну общую точку, называется касательной (на рисунке отрезок CD).

Прямая, имеющая с окружностью две общие точки, называется секущей (отрезок NC).

Свойства касательной и секущей

1. Касательная перпендикулярна радиусу, проведенному в точку касания.

2. Отрезки касательных, проведенных из одной точки, равны.

3. Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: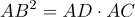

Вписанные и центральные углы   

Вписанная окружность

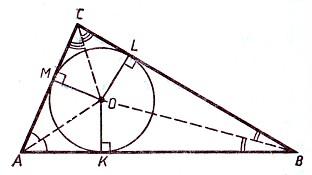
Если все стороны треугольника касаются окружности, то окружность называется вписанной в треугольник, а треугольник - описанным около этой окружности.

Теорема. В любой треугольник можно вписать окружность и при этом только одну.

Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.

Описанная окружность

Если все вершины многоугольника лежат на окружности, то окружность называется описанной около треугольника, а треугольник - вписанным в эту окружность.

Теорема. Около любого треугольника можно описать окружность и при этом только одну.

Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.

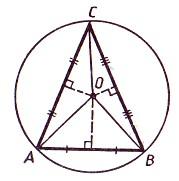
Равносторонний треугольник

Радиус описанной около равностороннего треугольника окружности определяется по формуле:

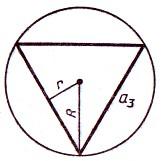
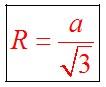
Радиус вписанной в равносторонний треугольник окружности определяется по формуле:

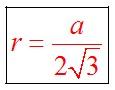
Прямоугольный треугольник

Центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы.

Радиус описанной около прямоугольного треугольника окружности равен длине медианы, проведенной к гипотенузе.

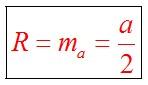
Радиус вписанной в прямоугольный треугольник окружности определяется по формуле: