Министерство образования Пензенской области
ГАПОУ ПО «Кузнецкий колледж электронных технологий»
Методические рекомендации
практического занятия
по учебной дисциплине
ЕН. 01 Математика
на тему: «Решение дифференциальных уравнений»
Кузнецк 2019
Пояснительная записка.
Методические рекомендации к практическому занятию по учебной дисциплине ЕН.01 Математика на тему «Решение дифференциальных уравнений» предназначено для студентов 2 курса специальности 15.02.15 «Технология металлообрабатывающего производства». Рекомендации содержат теоретический материал и примеры выполнения, что позволяет студентам легко выполнить все поставленные задачи.
Выполнение практического занятия направлено на обобщение, систематизацию, углубление теоретических знаний учебной дисциплины; формирование умений применять полученные знания в практической деятельности; на развитие аналитических, проектировочных, конструктивных умений; выработку самостоятельности, ответственности и творческой инициативы.
Для выполнения работы, студент обязан знать:
- понятие дифференциального уравнения;
- алгоритмы решения дифференциальных уравнений с разделяющимися переменными, обыкновенных дифференциальных уравнений 1-го порядка с одной неизвестной функцией, линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Уметь:
- применять различные методы для решения дифференциальных уравнений.
Тема: «Решение дифференциальных уравнений»
Цель: формирование умений и навыков решения дифференциальных уравнений.
Методические указания и теоретические сведения к практической работе
1 Дифференциальные уравнения – это уравнения, содержащие искомые функции, их производные различных порядков и независимые переменные.
2 Порядком дифференциального уравнения называется наивысший порядок, входящих в него производных.
3 Решить дифференциальное уравнение – это значит, найти множество функций y = f (x) + C, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.
4 Частное решение дифференциального уравнения — это решение, не содержащее произвольных постоянных.
5 Обыкновенным дифференциальным уравнением 1-го порядка с одной неизвестной функцией называется соотношение F (x, у, у') = 0 между независимым переменным х, искомой функцией у и еѐ производной.
6 Если уравнение может быть разрешено относительно производной, то получается уравнение y' = f (x, у), разрешенное относительно производной.
7 Дифференциальные уравнения f(y) dy = g(x) dx называют уравнениями с разделенными переменными.
8 Линейное уравнение первого порядка – это уравнение вида:

9 Если q(x) = 0, то уравнение называется однородным, если q(x) ≠ 0, то уравнение неоднородное.
10 Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:  , где p и q – константы (числа), а в правой части – строго ноль.
, где p и q – константы (числа), а в правой части – строго ноль.
Примеры
Задание 1: Найдите общее решение уравнения  .
.
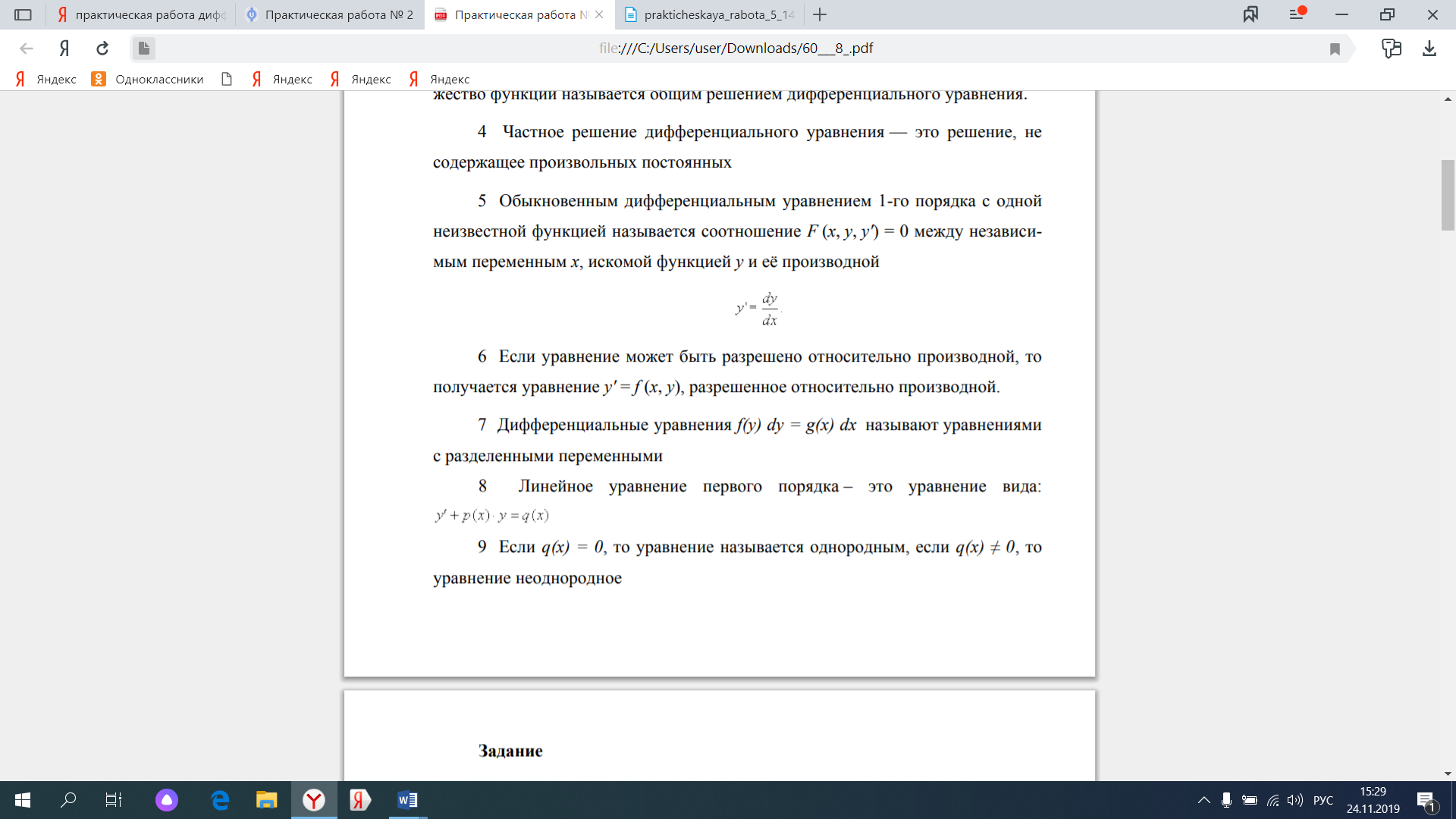
Решение: Разделив переменные, имеем 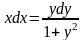 . Интегрируем обе части полученного уравнения:
. Интегрируем обе части полученного уравнения:
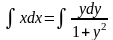 ;
; 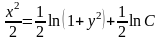 .
.
Так как произвольная постоянная  может принимать любые числовые значения, то для удобства дальнейших преобразований вместо
может принимать любые числовые значения, то для удобства дальнейших преобразований вместо  мы написали
мы написали 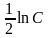 . Потенцируя последнее равенство, получим
. Потенцируя последнее равенство, получим  .
.
Это и есть общее решение данного уравнения.
Задание 2: Найти частное решение уравнения 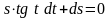 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  при
при  .
.
Решение: Разделив переменные, имеем  . Проинтегрируем обе части полученного уравнения:
. Проинтегрируем обе части полученного уравнения:
 ;
;  ,
,
или
 ,
, 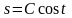 .
.
Это общее решение данного уравнения. Для нахождения значения произвольной постоянной  подставим значения
подставим значения  и
и  в выражение для общего решения:
в выражение для общего решения: 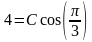 , или
, или 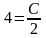 , откуда
, откуда  .Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид
.Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид  .
.
Задание 3: Найдите общее решение уравнения .
Решение: Это линейное уравнение: здесь  ,
,  . Положим
. Положим  и продифференцируем это равенство по
и продифференцируем это равенство по  :
:
 .
.
Подставив теперь выражения для  и
и  в данное уравнение, получим
в данное уравнение, получим
,
или
. (*)
Так как одну из вспомогательных функций  или
или  можно выбрать произвольно, то в качестве
можно выбрать произвольно, то в качестве  возьмем одно из частных решений уравнения
возьмем одно из частных решений уравнения  . Разделив в этом уравнении переменные и проинтегрируя, имеем
. Разделив в этом уравнении переменные и проинтегрируя, имеем  , ;
, ;  ,
,  (произвольную постоянную
(произвольную постоянную  принимаем равной нулю, так как находим одно из частных решений).
принимаем равной нулю, так как находим одно из частных решений).
Подставим теперь выражение для  в уравнение (*); тогда получим уравнение , или
в уравнение (*); тогда получим уравнение , или  .
.
Отсюда находим  ; .
; .
Зная  и
и  , теперь получим общее решение данного уравнения:
, теперь получим общее решение данного уравнения:
.
Задание 4: Решить уравнение: .
Решение: Составим характеристическое уравнение и найдем его корни:  . Отсюда следует, что
. Отсюда следует, что  ,
,  . Так как корни характеристического уравнения действительные и разные, то общее решение данного дифференциального уравнения согласно формуле (3) запишется так:
. Так как корни характеристического уравнения действительные и разные, то общее решение данного дифференциального уравнения согласно формуле (3) запишется так:  .
.
Задание 5: Найти частное решение уравнения , если  и
и  при
при  .
.
Решение: Составим характеристическое уравнение  . Решая его, получим,
. Решая его, получим,  ,
,  . Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения имеет вид:
. Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения имеет вид:  , то есть
, то есть  .
.
Для нахождения искомого частного решения нужно определить значения постоянных  и
и  . Подставив в общее решение значения
. Подставив в общее решение значения  и
и  , получим
, получим  .
.
Продифференцировав общее решение и подставив в полученное выражение значения  и
и  , имеем , отсюда следует, что
, имеем , отсюда следует, что  . Из данного выражения находим:
. Из данного выражения находим:  , .
, .
Таким образом, искомое частное решение имеет вид  .
.
Задание 6: Решить уравнение .
Решение: Составим характеристическое уравнение и найдем его корни:  ,
,  . Характеристическое уравнение имеет равные действительные корни; поэтому согласно формуле (4) общее решение данного дифференциального уравнения записывается в виде .
. Характеристическое уравнение имеет равные действительные корни; поэтому согласно формуле (4) общее решение данного дифференциального уравнения записывается в виде .
Контрольные вопросы.
Какое уравнение называется дифференциальным?
Что называется решением дифференциального уравнения?
Какое решение дифференциального уравнения называется общим?
Какое решение дифференциального уравнения называется частным?
Какие дифференциальные уравнения называются уравнениями первого порядка?
Какие дифференциальные уравнения называются уравнениями с разделяющимися переменными?
Какие дифференциальные уравнения называются уравнениями второго порядка?
Какие уравнения называются линейными однородными дифференциальными уравнениями второго порядка?
Какой вид имеет характеристическое уравнение? Для чего необходимо его нахождение?
Какие случаи возможны при нахождении общего решения дифференциального уравнения второго порядка?
Выполните задания в соответствии со своим вариантом
Вариант 1
1. Найти общее решение дифференциального уравнения к разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.

3.Найти решение однородного дифференциального уравнения первого порядка.

4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.

Вариант 2
1. Найти общее решение дифференциального уравнения c разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
3.Найти решение однородного дифференциального уравнения первого порядка.

4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.

Вариант 3
1. Найти общее решение дифференциального уравнения c разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
3.Найти решение однородного дифференциального уравнения первого порядка.

4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.
Вариант 4
1. Найти общее решение дифференциального уравнения c разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
3.Найти решение однородного дифференциального уравнения первого порядка.

4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.
Вариант 5
1. Найти общее решение дифференциального уравнения к разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
3.Найти решение однородного дифференциального уравнения первого порядка.
4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.
Вариант 6
1. Найти общее решение дифференциального уравнения к разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
3.Найти решение однородного дифференциального уравнения первого порядка.
4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.
Ссылки на используемые источники:
http://gunkoiren.ucoz.ru/_ld/0/60___8_.pdf
https://nsportal.ru/npo-spo/estestvennye-nauki/library/2016/12/12/sbornik-prakticheskih-zanyatiy-en-01matematika
https://infourok.ru/prakticheskaya_rabota_po_matematike_na_temu_differencialnye_uravneniya-533467.htm








 .
.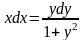 . Интегрируем обе части полученного уравнения:
. Интегрируем обе части полученного уравнения: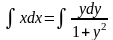 ;
; 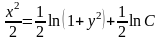 .
. может принимать любые числовые значения, то для удобства дальнейших преобразований вместо
может принимать любые числовые значения, то для удобства дальнейших преобразований вместо 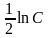 . Потенцируя последнее равенство, получим
. Потенцируя последнее равенство, получим  .
. 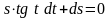 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  при
при  .
. . Проинтегрируем обе части полученного уравнения:
. Проинтегрируем обе части полученного уравнения: ;
;  ,
, ,
, 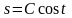 .
.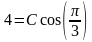 , или
, или 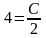 , откуда
, откуда  .Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид
.Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид 

















