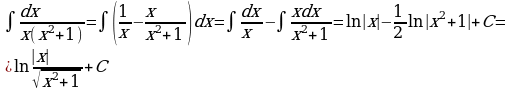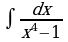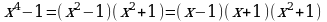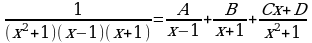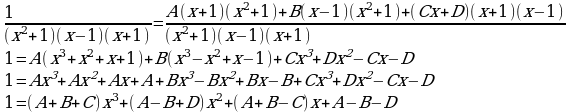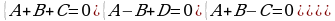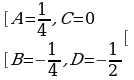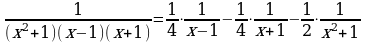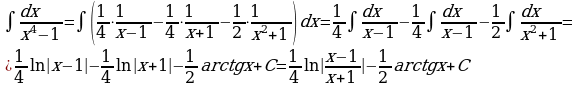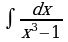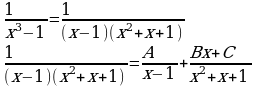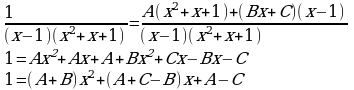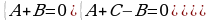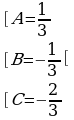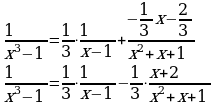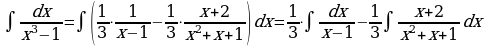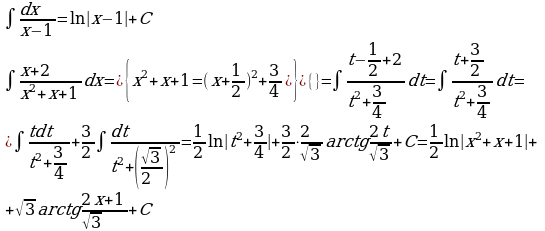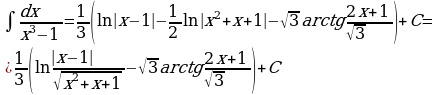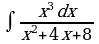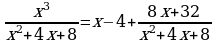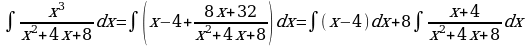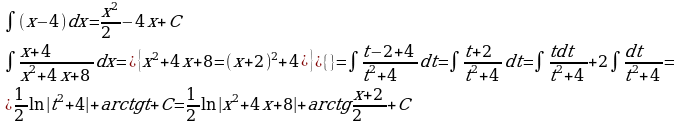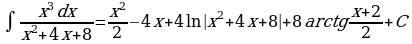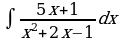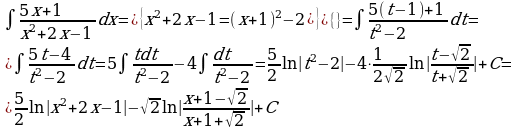Тирский Александр Сергеевич., учитель математики РГ «Эврика» г Олекминска
Интегрирование рациональных функций
Понятие о рациональных функциях
Функция вида
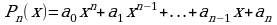 (1)
(1)
где n – натуральное число, 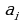 - постоянные коэффициенты, называется многочленом или целой рациональной функцией. Число n называется степенью многочлена.
- постоянные коэффициенты, называется многочленом или целой рациональной функцией. Число n называется степенью многочлена.
Корнем многочлена называется такое значение переменной 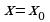 , при котором многочлен обращается в нуль, т.е.
, при котором многочлен обращается в нуль, т.е. 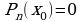 .
.
Теорема 1
Если 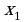 есть корень многочлена
есть корень многочлена 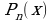 , то многочлен без остатка делится на
, то многочлен без остатка делится на 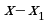 , т.е.
, т.е.
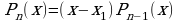 (2)
(2)
Где 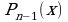 - многочлен степени n-1.
- многочлен степени n-1.
Теорема 2
Всякий многочлен n-ой степени имеет по крайней мере один корень, действительный или комплексный.
Теорема 3
Если многочлен 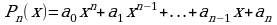 тождественно равен нулю, то все его коэффициенты равны нулю.
тождественно равен нулю, то все его коэффициенты равны нулю.
Теорема 4
Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого.
Известно, что каждый многочлен с действительными коэффициентами единственным образом разлагается на линейные и квадратические множители вида: х-а и 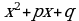 , где р и q - действительные коэффициенты, причем квадратические множители не имеют действительных корней и, следовательно, не разложимы на линейные множители.
, где р и q - действительные коэффициенты, причем квадратические множители не имеют действительных корней и, следовательно, не разложимы на линейные множители.
Продемонстрируем на примерах разложения многочленов на множители:
1) 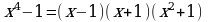
2) 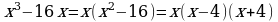
3) 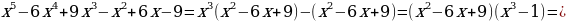
Дробно – рациональной функцией или рациональной дробью называется функция, равная отношению двух многочленов, т.е.
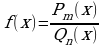 , где
, где 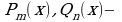 многочлены степени m и n соответственно.
многочлены степени m и n соответственно.
Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя. В противном случае дробь называется неправильной.
Следует заметить, что всякую неправильную дробь 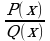 можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби
можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби 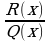 , т.е.
, т.е. 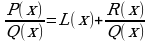 , где R(x) - остаток от деления, а L(x) - целая часть.
, где R(x) - остаток от деления, а L(x) - целая часть.
Будем теперь рассматривать правильные рациональные дроби определенного типа.
Правильные рациональные дроби вида:
1) 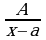 2)
2) 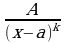 3)
3) 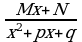 4)
4) 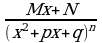 ,
,
где 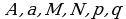 - действительные числа, называются простейшими рациональными дробями I,II,III,IV типов.
- действительные числа, называются простейшими рациональными дробями I,II,III,IV типов.
Замечание: Предполагается, что для дробей III,IV многочлен,
стоящий в знаменателе, не имеет действительных
корней.
Теорема 5
Всякую правильную рациональную дробь 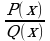 , знаменатель которой разложен на множители:
, знаменатель которой разложен на множители:
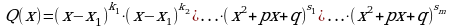
можно представить и притом единственным образом, в виде следующей суммы простейших дробей: 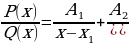 (3)
(3)
Поясним формулировку теоремы на примерах
1) 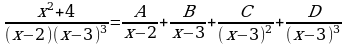
2) 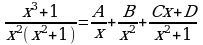
3) 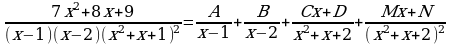
Для нахождения неопределенных коэффициентов в правой части разложения, можно применить метод сравнивания коэффициентов. Суть метода такова:
В правой части равенства (3.1.3) приведем к общему знаменателю Q(x); в результате получим тождество
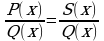 (4)
(4)
где S(x) – многочлен с неопределенными коэффициентами.
так как в полученном тождестве знаменатели равны, то тождественно равны и числители 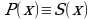 .
.
Приравнивая коэффициенты при одинаковых степенях х (по теореме 3.1.4) в обеих частях тождества (4), получим систему линейных уравнений, из которой и определим искомые коэффициенты.
Рассмотрим пример демонстрирующий методику применения описанного выше метода.
Пример.
Представить дробь 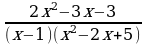 в виде суммы простейших дробей
в виде суммы простейших дробей
Решение:
Согласно теореме (5) имеем:
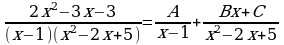
Т.е. 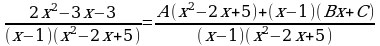
Отсюда следует:
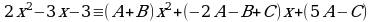
Приравнивая коэффициенты при 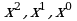 , получаем:
, получаем:
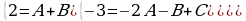
Решая систему, находим ее решение: 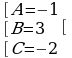
Следовательно, получаем:
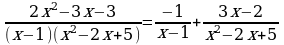
Интегрирование простейших рациональных дробей
Найдем интегралы от простейших рациональных дробей
1) 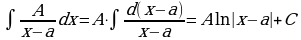
2) 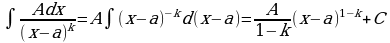
3) Рассмотрим интеграл 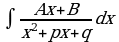 , в числителе подынтегральной функции которого стоит линейный двучлен, а в знаменателе квадратный трехчлен, не имеющий корней. Интегралы такого типа вычисляются путем выделения полного квадрата в знаменателе подынтегральной функции.
, в числителе подынтегральной функции которого стоит линейный двучлен, а в знаменателе квадратный трехчлен, не имеющий корней. Интегралы такого типа вычисляются путем выделения полного квадрата в знаменателе подынтегральной функции.
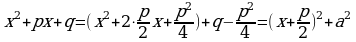 ,где
,где 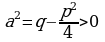 . Сделаем замену
. Сделаем замену 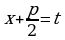 , тогда
, тогда 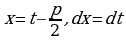 . Подставляя это в исходный и интеграл, получим
. Подставляя это в исходный и интеграл, получим
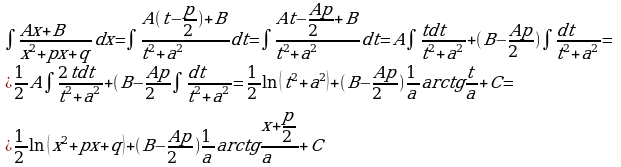
Примеры:
Найти интегралы
1. 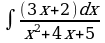


Решение:
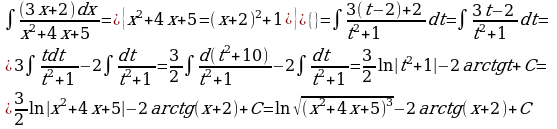
2). 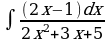
Решение:
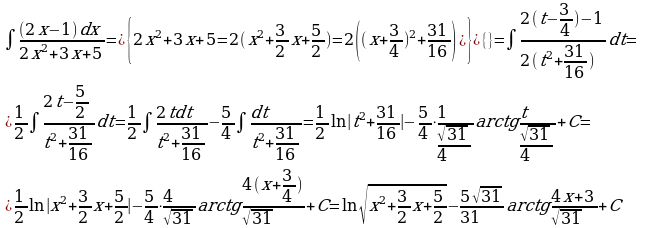
4. 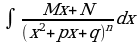 , где знаменатель не имеет действительных
, где знаменатель не имеет действительных
корней.
Данный интеграл подстановкой 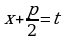 , сводится к сумме двух интегралов:
, сводится к сумме двух интегралов:
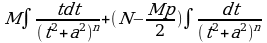 ,
, 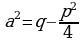
Первый интеграл легко вычисляется:
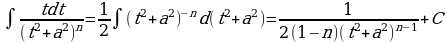
Вычислим второй интеграл:
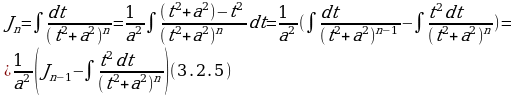 (5)
(5)
К последнему интегралу применяем интегрирование по частям. Положим 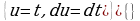
Тогда 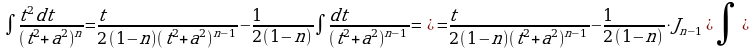
Подставляя найденный интеграл в равенство (5) получаем:
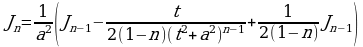 ,
,
Т.е.
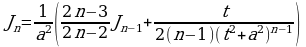 .
.
Полученная формула позволяет найти интеграл 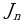 для любого натурального числа
для любого натурального числа 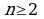 .
.
Рассмотрим пример.
Найти интеграл 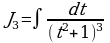
Решение:
Здесь а=1, n=3. Так как 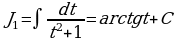 , то
, то
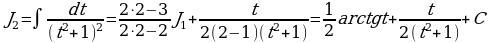 ,
,
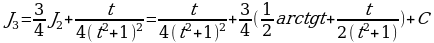 .
.
интегрирование рациональных дробей (ПРАКТИКА)
Рассмотренный в предыдущих пунктах материал позволяет сформулировать общее правило интегрирования рациональных дробей.
если дробь неправильная, то ее необходимо представить в виде суммы многочлена и правильной дроби.
Разложив знаменатель правильной дроби на множители, представить ее в виде суммы простейших рациональных дробей.
Проинтегрировать многочлен и полученную сумму простейших дробей.
Рассмотрим несколько примеров:
Вычислить интегралы
1) 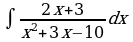
Решение:
Выпишем отдельно подынтегральную функцию, и
разложим знаменатель дроби на линейные множители:
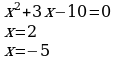 Следовательно,
Следовательно, 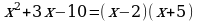
Теперь разложим функцию на простейшие дроби:
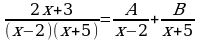
Теперь определяем неизвестные коэффициенты методом их сравнивания.

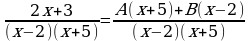 ,
,
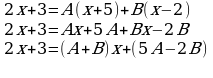
Теперь составляем систему уравнений для нахождения коэффициентов А и В
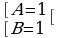
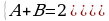
Таким образом, получаем:
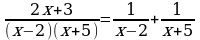 Интегрируя, получаем
Интегрируя, получаем
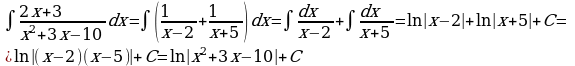
2) 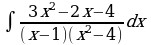
Решение:
Заметим, что данная дробь правильная. Выпишем отдельно подынтегральную функцию и разложим знаменатель дроби на линейные множители:
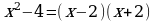
Теперь разложим подынтегральную функцию на простейшие дроби:
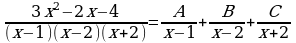
Приводя к общему знаменателю справа, получаем:
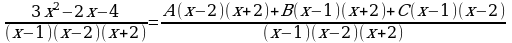
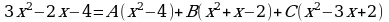
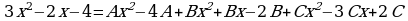
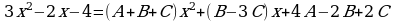
Составляем систему для определения коэффициентов, на основании теоремы о равенстве многочленов
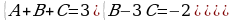
Решая систему получаем: 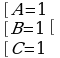 . Таким образом, получаем разложение
. Таким образом, получаем разложение
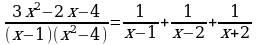
Интегрируя получаем:
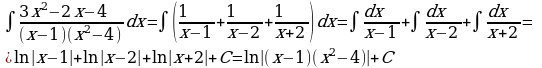
Замечание: В дальнейших примерах подробное пояснение опустим, т.к. оно такое же как и в первых двух.
3) 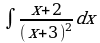
Решение:
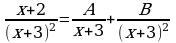
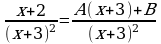 ,
, 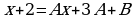
Составляем систему:
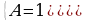
Решая систему, получаем,
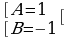
Таким образом, получаем разложение:
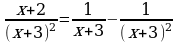
Интегрируя, получаем,
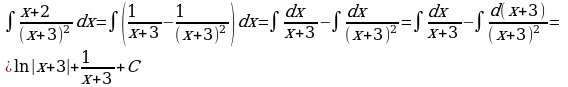
4) 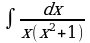
Решение:
Разложим подынтегральную функцию на простейшие дроби:
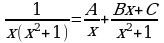
Приводя к общему знаменателю справа, получаем
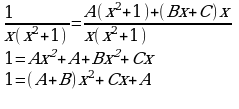
Составляем систему:
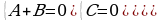
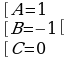
Таким образом, получаем разложение:
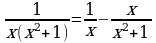 Интегрируя, получаем
Интегрируя, получаем
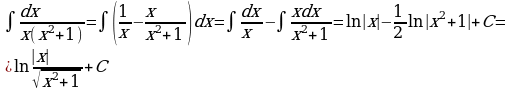
5) 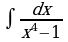
Решение:
Разложим знаменатель подынтегральной функции на множители
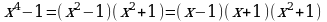
Теперь разложим подынтегральную функцию на простейшие дроби:
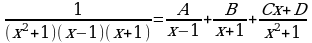
Приводя к общему знаменателю справа, получаем
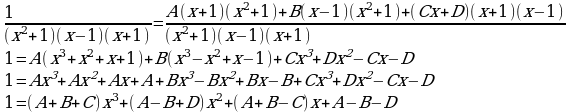
Составляем систему:
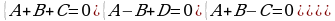
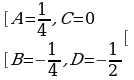
Таким образом, получаем разложение:
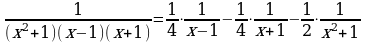
Интегрируя, получаем
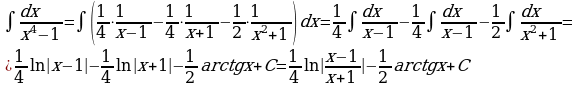
6) 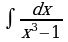
Решение:
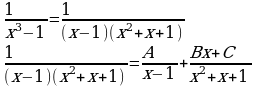
Приводя к общему знаменателю справа, получаем
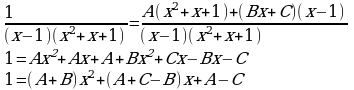
Теперь составляем систему:
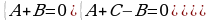
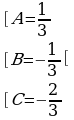
Таким образом, получаем разложение
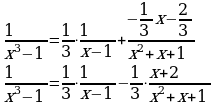
Интегрируя, получаем
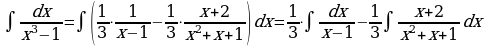
Вычислим отдельно каждый из получившихся интегралов:
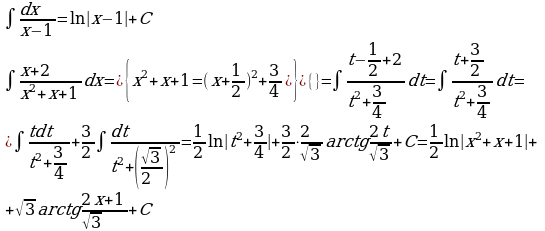
Подставляя, окончательно получаем
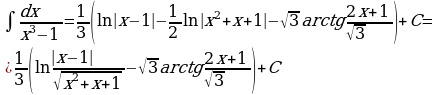
7) 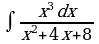
Решение:
Подынтегральная функция представляет собой неправильную рациональную дробь, поэтому выделим сначала целую часть дроби, поделив числитель на знаменатель. В результате получим:
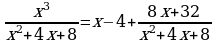
Интегрируя. получаем:
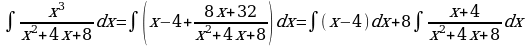
Вычислим отдельно каждый интеграл:
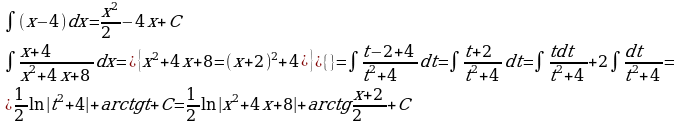
 Таким образом, подставляя получаем,
Таким образом, подставляя получаем,
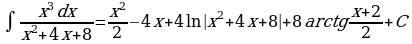
Замечание:
Рассмотрим интеграл 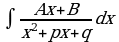 , где знаменатель подынтегральной функции разлагается на линейные множители. Данный интеграл «внешне похож» на интеграл от простейшей дроби третьего типа, однако он таковым не является в силу разложимости знаменателя. По идее для вычисления интеграла необходимо разложить функцию на простейшие дроби и вычислять интеграл как в примере 1. Но если знаменатель функции имеет иррациональные корни, то решение получается достаточно трудоемким. В таких случаях интеграл можно вычислить как интеграл от простейшей дроби третьего типа, т.е выделив в знаменателе дроби полный квадрат. Приведем пример.
, где знаменатель подынтегральной функции разлагается на линейные множители. Данный интеграл «внешне похож» на интеграл от простейшей дроби третьего типа, однако он таковым не является в силу разложимости знаменателя. По идее для вычисления интеграла необходимо разложить функцию на простейшие дроби и вычислять интеграл как в примере 1. Но если знаменатель функции имеет иррациональные корни, то решение получается достаточно трудоемким. В таких случаях интеграл можно вычислить как интеграл от простейшей дроби третьего типа, т.е выделив в знаменателе дроби полный квадрат. Приведем пример.
8. 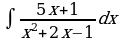
Решение:
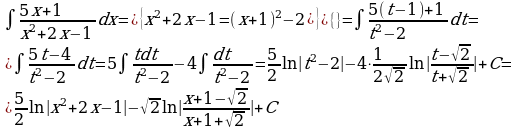
Итак, из вышерассмотренной теории и разобранных примеров, следует, что неопределенный интеграл от любой рациональной и дробно-рациональной функции всегда существует( на интервалах, в которых знаменатель дроби отличен от 0) и выражается через конечное число элементарных функций, а, именно, он является алгебраической суммой, членами которой могут быть лишь многочлены, рациональные дроби, натуральные логарифмы и арктангенсы.







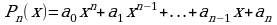 (1)
(1)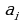 - постоянные коэффициенты, называется многочленом или целой рациональной функцией. Число n называется степенью многочлена.
- постоянные коэффициенты, называется многочленом или целой рациональной функцией. Число n называется степенью многочлена. 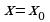 , при котором многочлен обращается в нуль, т.е.
, при котором многочлен обращается в нуль, т.е. 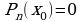 .
.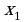 есть корень многочлена
есть корень многочлена 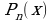 , то многочлен без остатка делится на
, то многочлен без остатка делится на 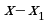 , т.е.
, т.е. 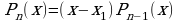 (2)
(2)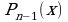 - многочлен степени n-1.
- многочлен степени n-1.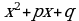 , где р и q - действительные коэффициенты, причем квадратические множители не имеют действительных корней и, следовательно, не разложимы на линейные множители.
, где р и q - действительные коэффициенты, причем квадратические множители не имеют действительных корней и, следовательно, не разложимы на линейные множители.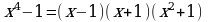
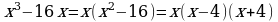
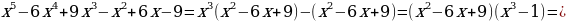
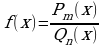 , где
, где 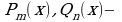 многочлены степени m и n соответственно.
многочлены степени m и n соответственно.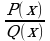 можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби
можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби 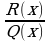 , т.е.
, т.е. 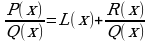 , где R(x) - остаток от деления, а L(x) - целая часть.
, где R(x) - остаток от деления, а L(x) - целая часть.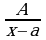 2)
2) 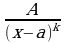 3)
3) 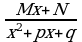 4)
4) 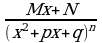 ,
,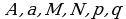 - действительные числа, называются простейшими рациональными дробями I,II,III,IV типов.
- действительные числа, называются простейшими рациональными дробями I,II,III,IV типов.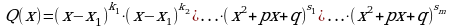
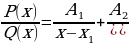 (3)
(3)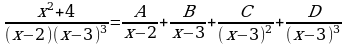
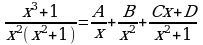
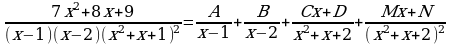
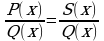 (4)
(4)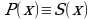 .
.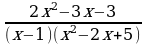 в виде суммы простейших дробей
в виде суммы простейших дробей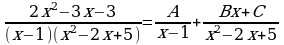
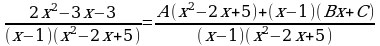
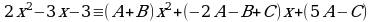
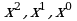 , получаем:
, получаем: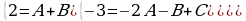
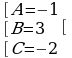
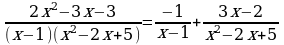
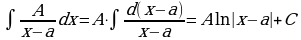
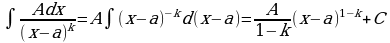
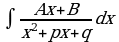 , в числителе подынтегральной функции которого стоит линейный двучлен, а в знаменателе квадратный трехчлен, не имеющий корней. Интегралы такого типа вычисляются путем выделения полного квадрата в знаменателе подынтегральной функции.
, в числителе подынтегральной функции которого стоит линейный двучлен, а в знаменателе квадратный трехчлен, не имеющий корней. Интегралы такого типа вычисляются путем выделения полного квадрата в знаменателе подынтегральной функции.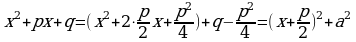 ,где
,где 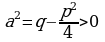 . Сделаем замену
. Сделаем замену 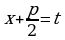 , тогда
, тогда 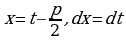 . Подставляя это в исходный и интеграл, получим
. Подставляя это в исходный и интеграл, получим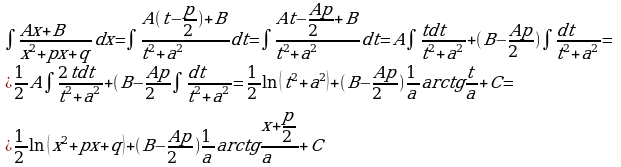
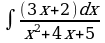

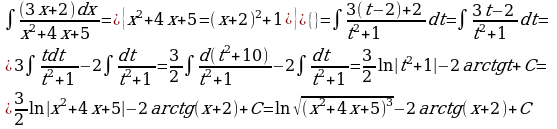
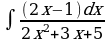
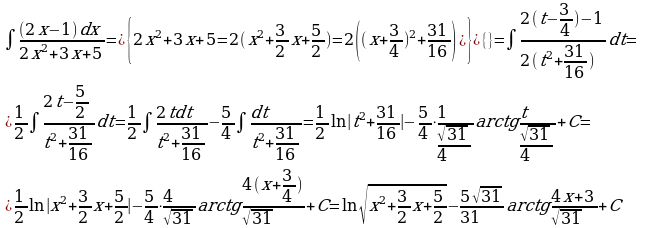
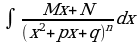 , где знаменатель не имеет действительных
, где знаменатель не имеет действительных 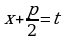 , сводится к сумме двух интегралов:
, сводится к сумме двух интегралов: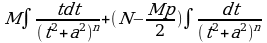 ,
, 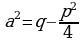
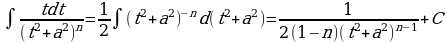
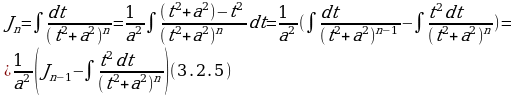 (5)
(5)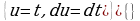
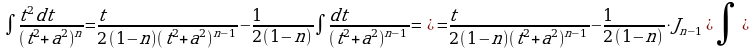
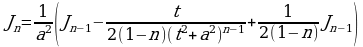 ,
, 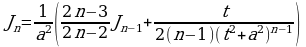 .
.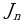 для любого натурального числа
для любого натурального числа 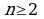 .
.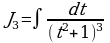
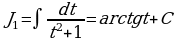 , то
, то 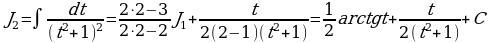 ,
, 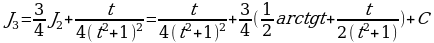 .
.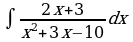
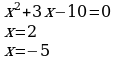 Следовательно,
Следовательно, 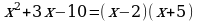
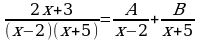
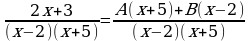 ,
, 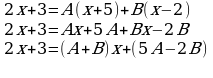
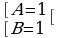
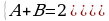
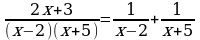 Интегрируя, получаем
Интегрируя, получаем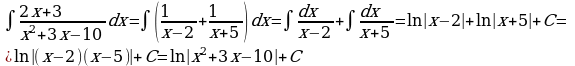
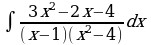
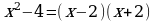
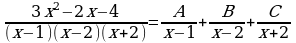
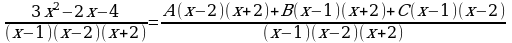
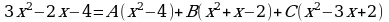
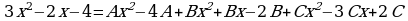
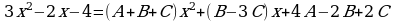
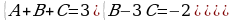
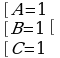 . Таким образом, получаем разложение
. Таким образом, получаем разложение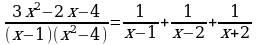
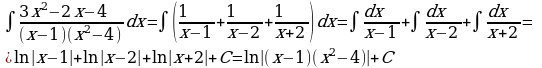
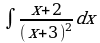
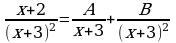
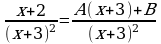 ,
, 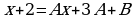
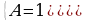
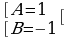
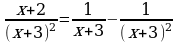
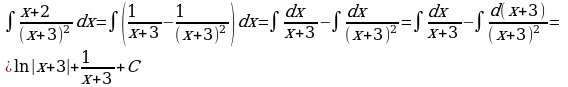
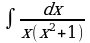
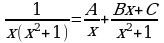
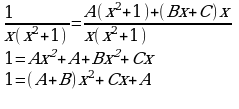
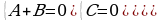
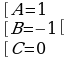
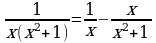 Интегрируя, получаем
Интегрируя, получаем