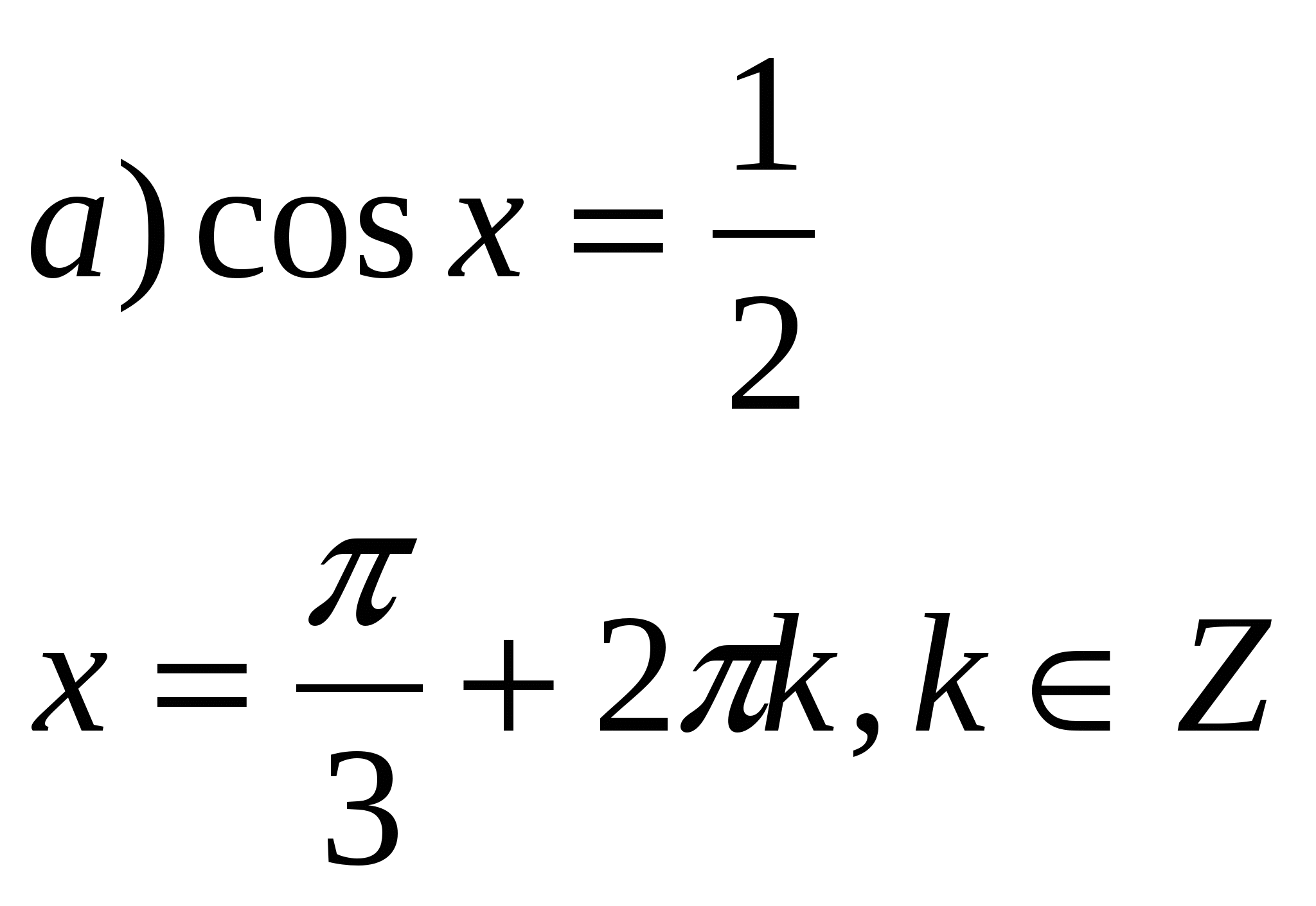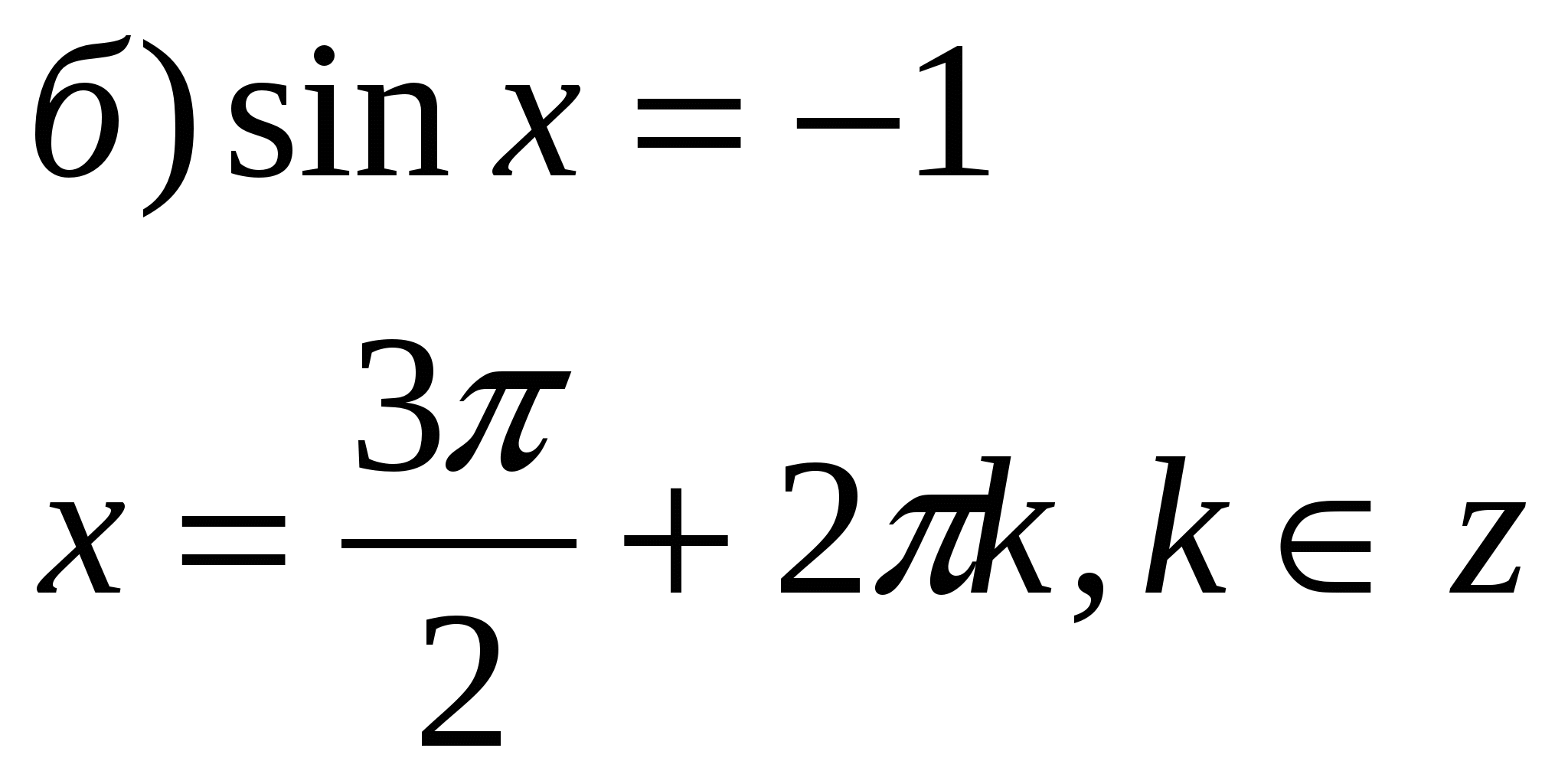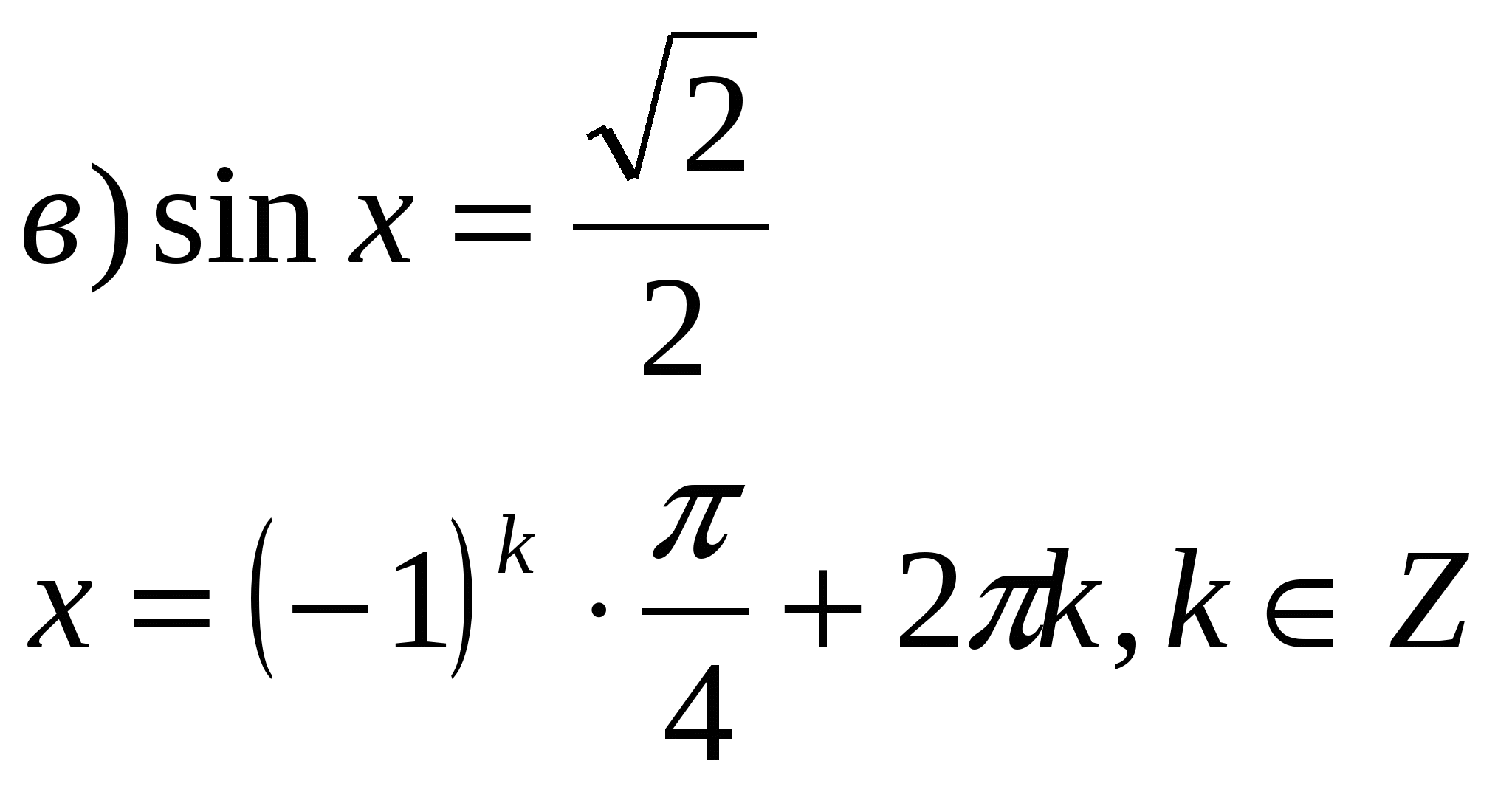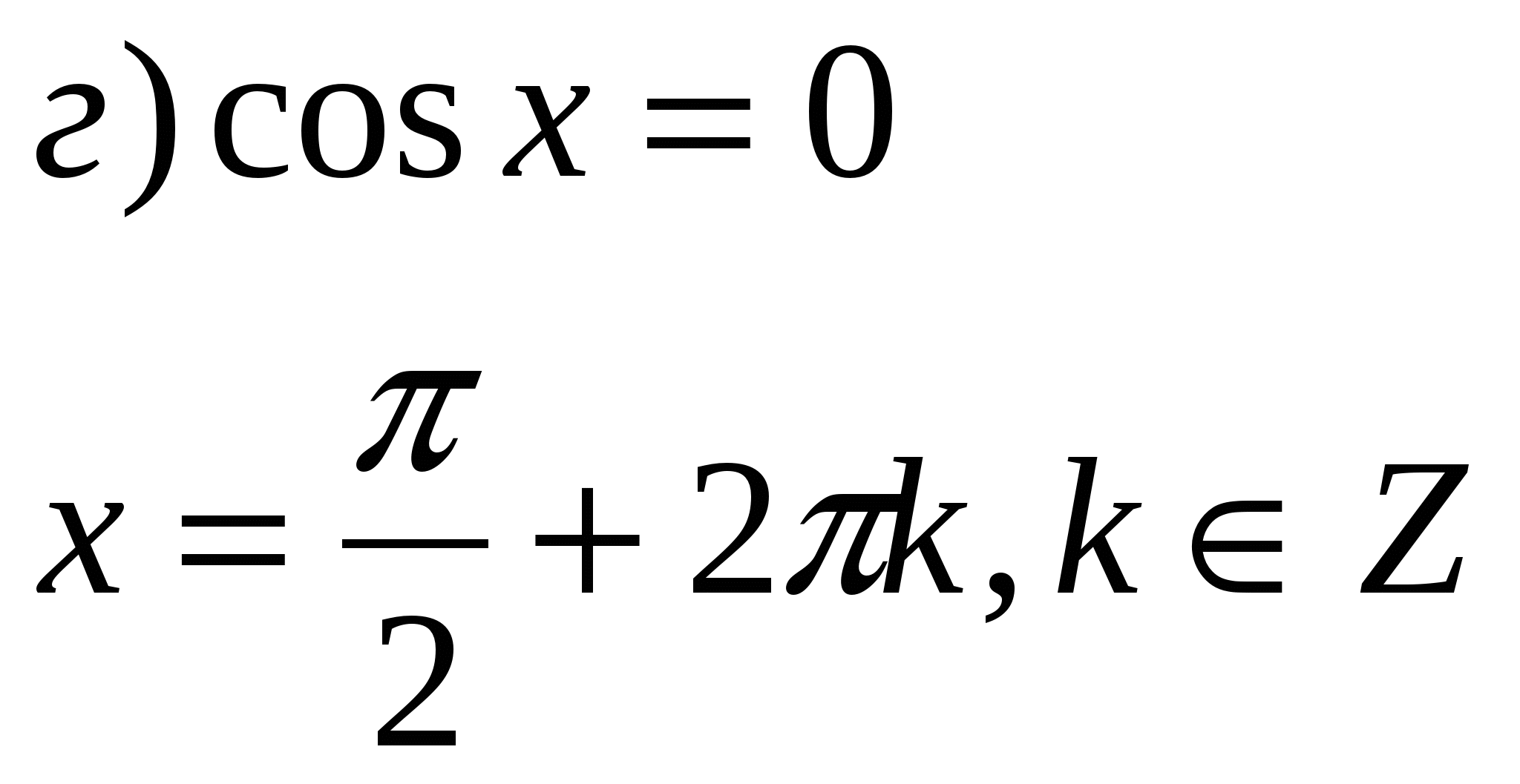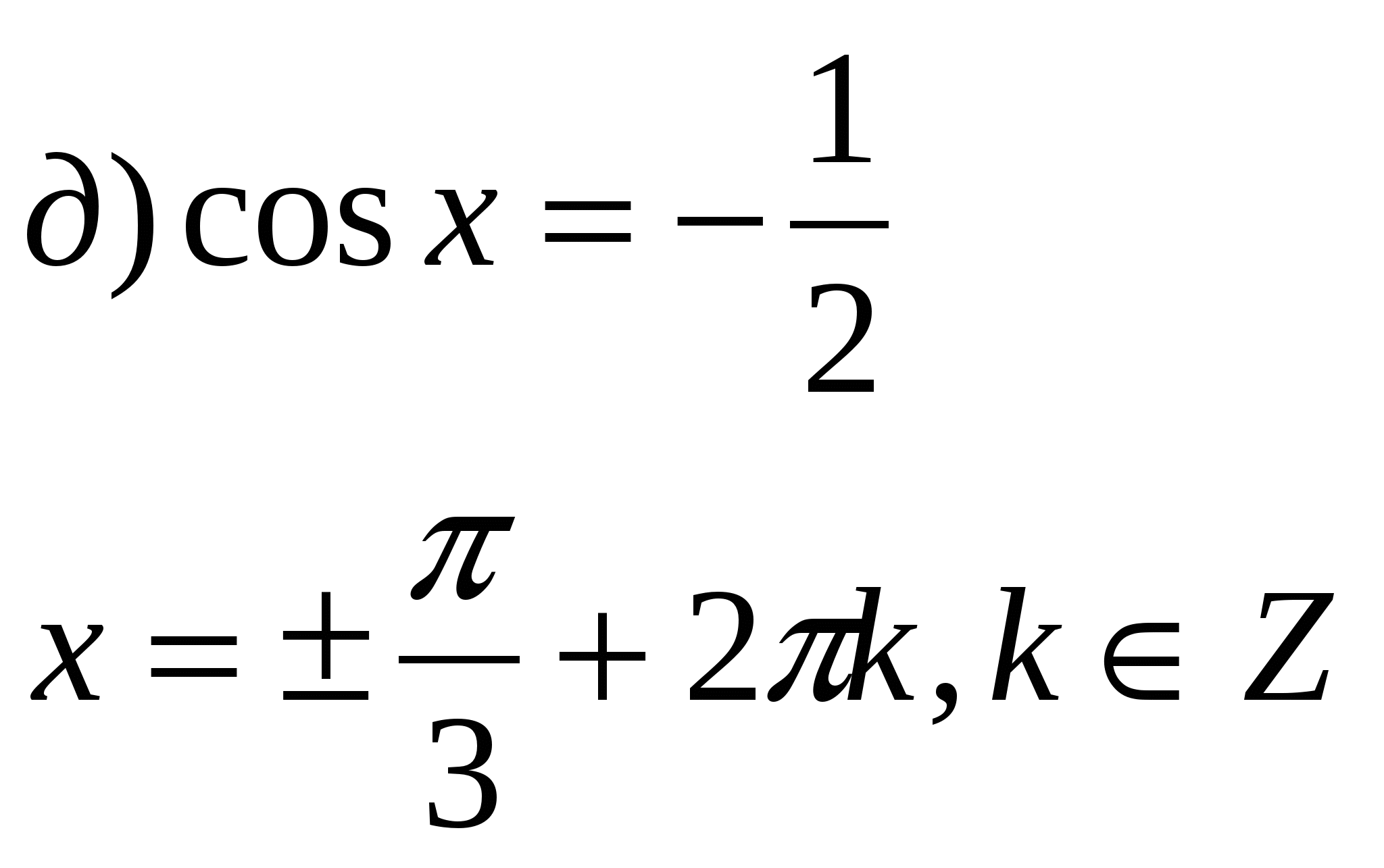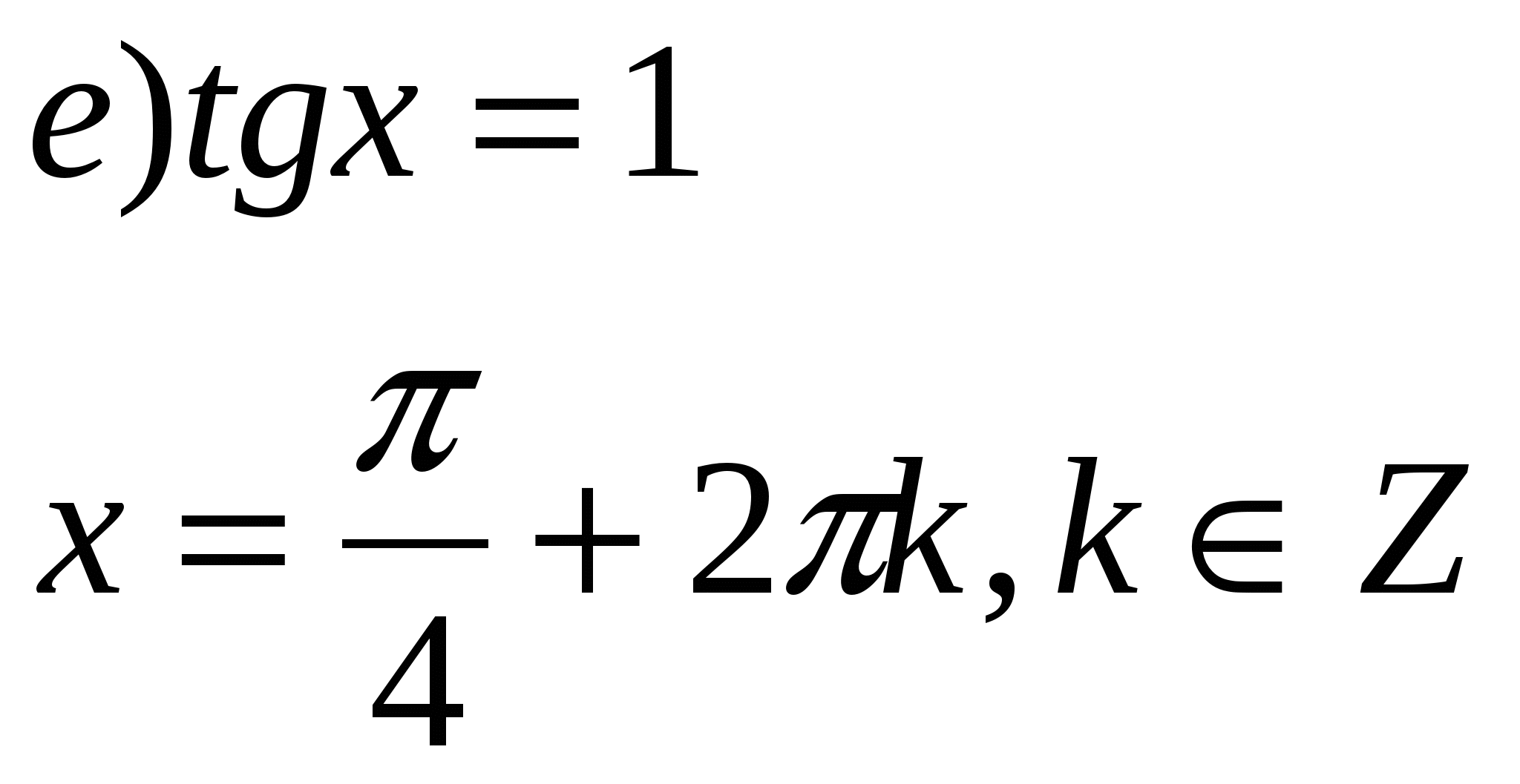Мастер класс по теме: «Решение тригонометрических уравнений».

Мастер класс

по теме: «Решение тригонометрических уравнений».

Цели занятия: 

- обобщить и систематизировать материал по данной теме: провести условную классификацию тригонометрических уравнений и методов их решения;

- способствовать формированию умений применять приёмы: сравнения, обобщения, выделения главного, развитию внимания, мышления, памяти;

- содействовать воспитанию интереса к математике, рациональной организации труда.

Задачи занятия: 

-повторить основные типы тригонометрических уравнений, наиболее типичные приёмы и методы их решения, систематизировать знания по данной теме.


Тип занятия :  обобщения и систематизации знаний.

Форма организации занятия: индивидуальная, фронтальная, групповая.

Китайская мудрость гласит: «Я слышу- я забываю, я вижу- я запоминаю, я делаю- я усваиваю». Сегодня у нас урок решения тригонометрических уравнений. Мы сегодня повторяем, обобщаем, приводим в систему виды тригонометрических уравнений, приёмы и методы их решения.

Сразу обратим внимание на некоторые обстоятельства, которые надо иметь в виду при решении. Во-первых, все общие правила , относящиеся к решению уравнений, имеют ту же силу. Во-вторых, существует условная классификация тригонометрических уравнений. И в- третьих, какой бы сложности ни было уравнение, в конце концов оно всё равно сведётся с решению простейшего тригонометрического уравнения.

При решении тригонометрических уравнений соблюдать общие правила:

- следить за равносильностью преобразований;

- не допускать потери корней;

- отбрасывать посторонние корни.

И последнее, для тригонометрических уравнений не существует единого метода решения. В каждом конкретном случае успех определяется, в частности знанием тригонометрических формул и навыками решения.


1.Записать решение простейших тригонометрических уравнений.

sin x=a sin x=1 sin x=0 sin x=-1 tg x=a
cos x=a cos x=1 cos x=0 cos x=-1 ctg x=a

Бонус:

При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2πn. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово -два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там -два.

Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн. А ещё наоборот бывает. Пропустит человек знак ±, доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)

2. Найдите ошибки в уравнениях.

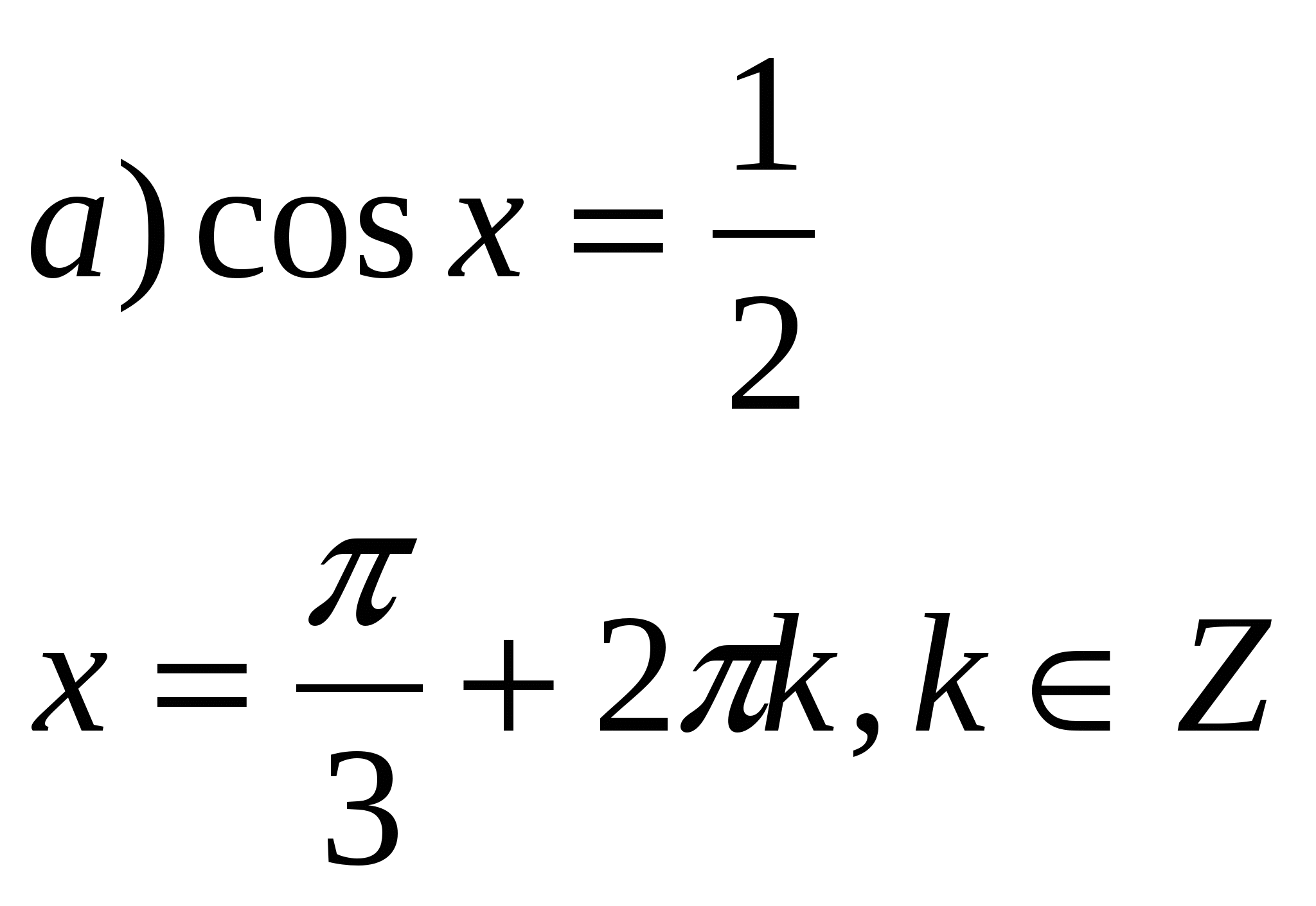
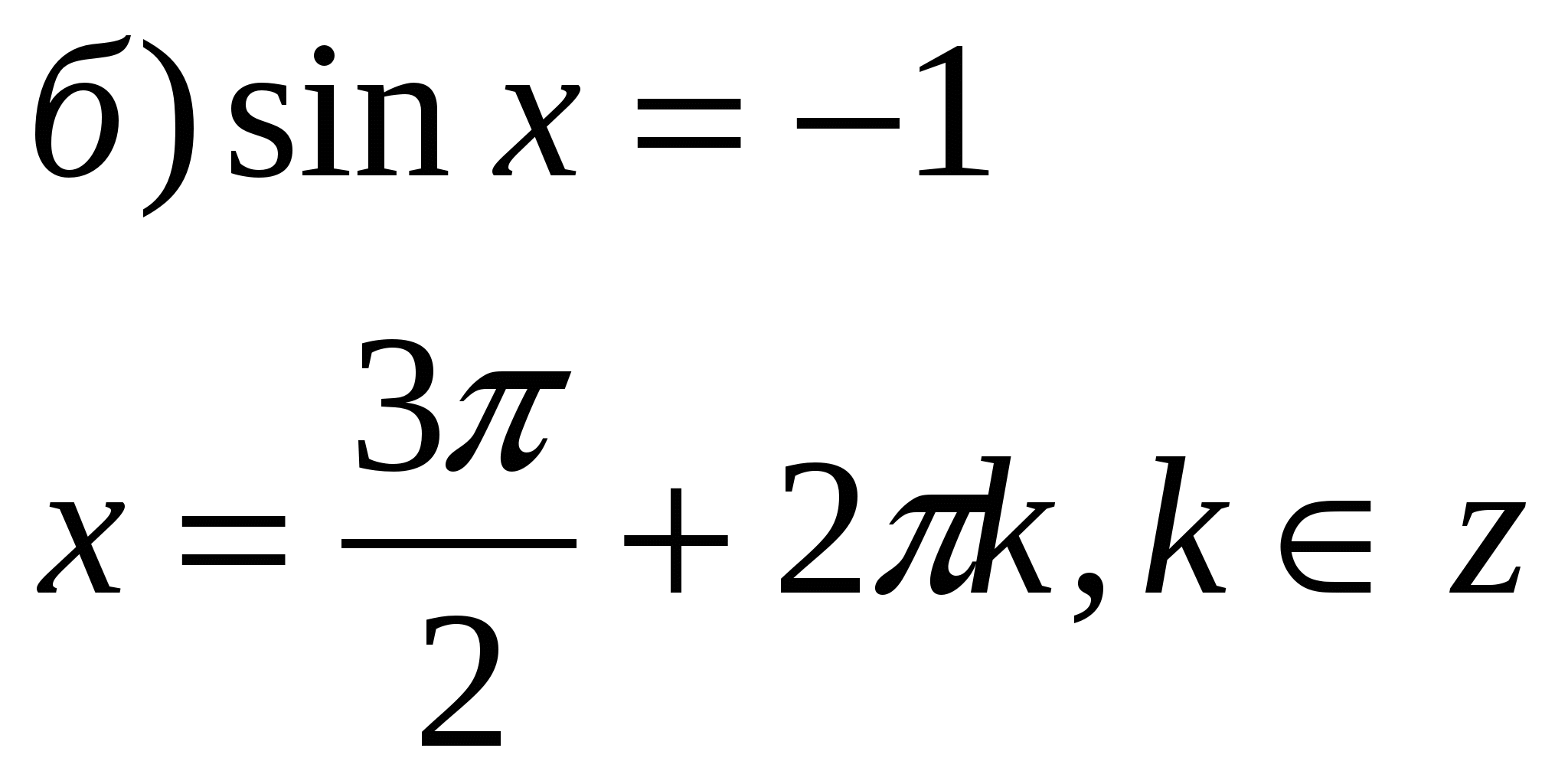
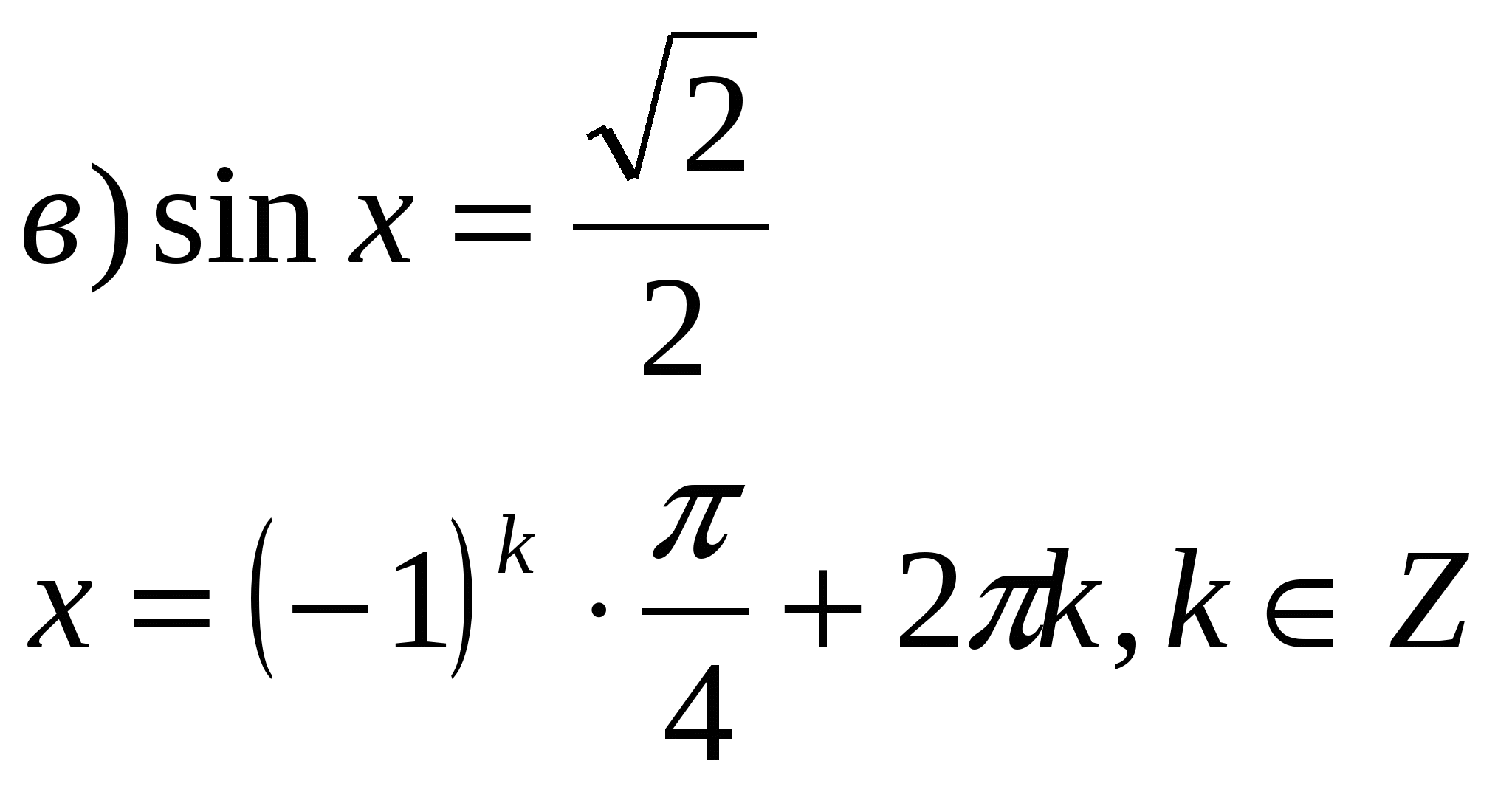
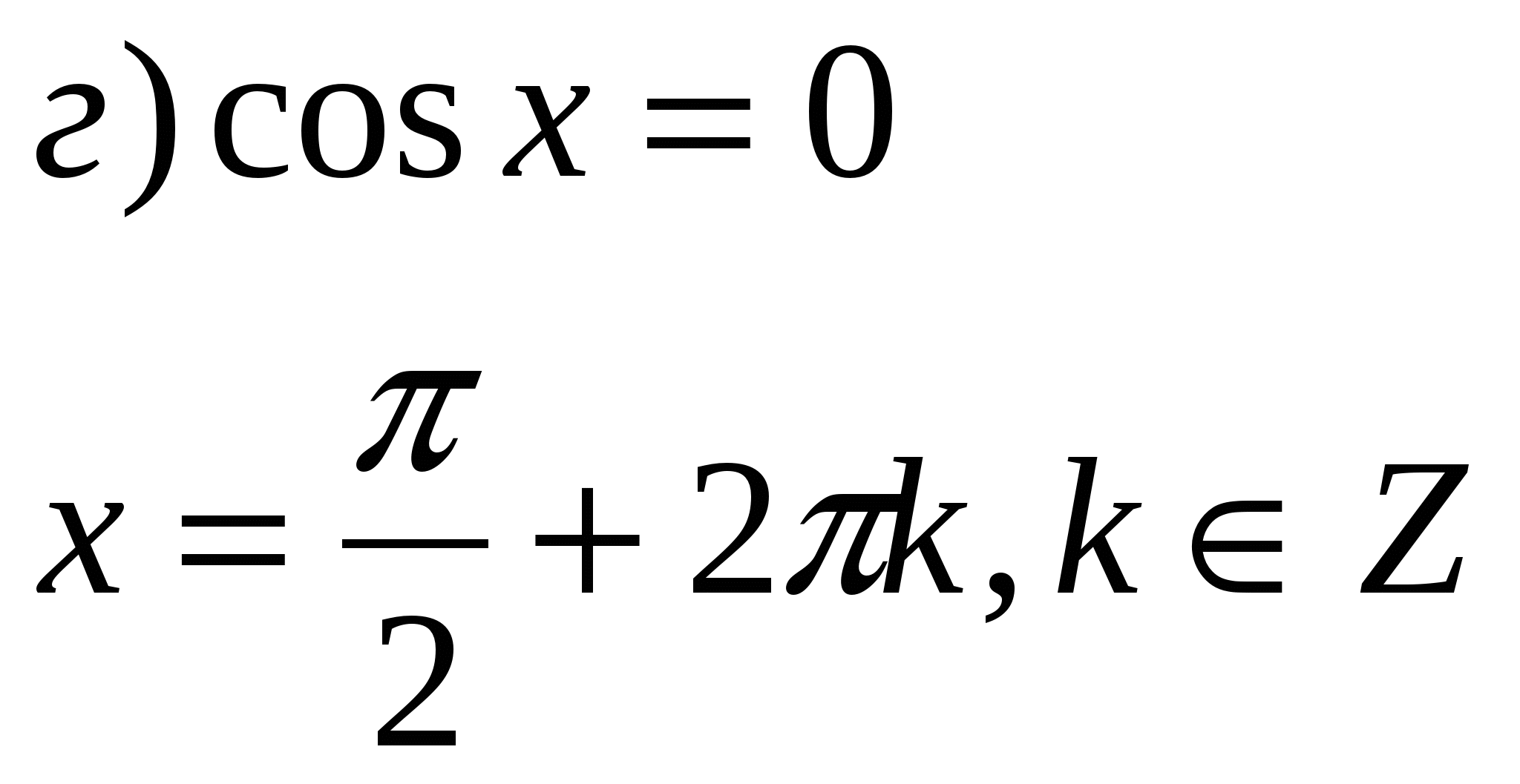
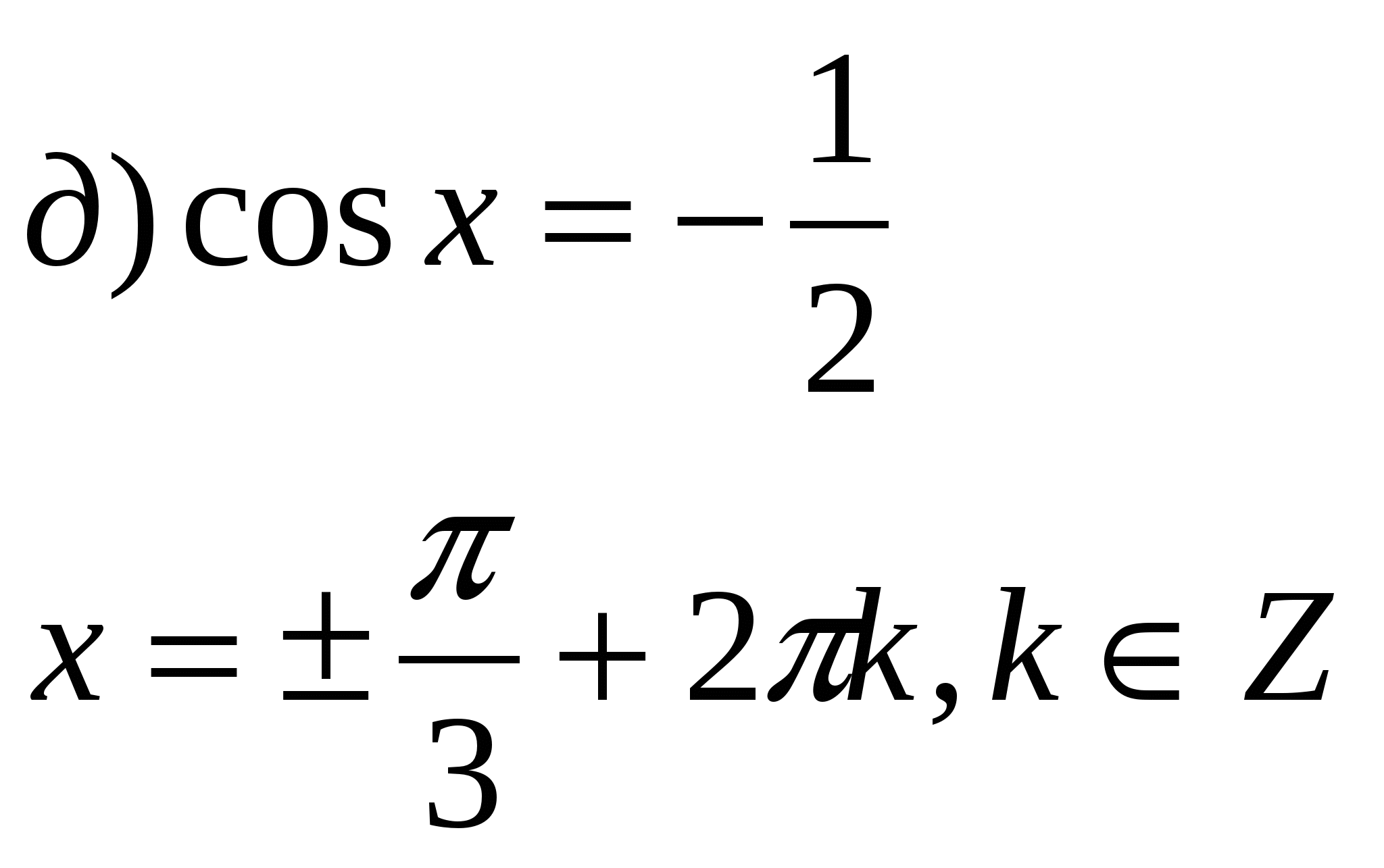
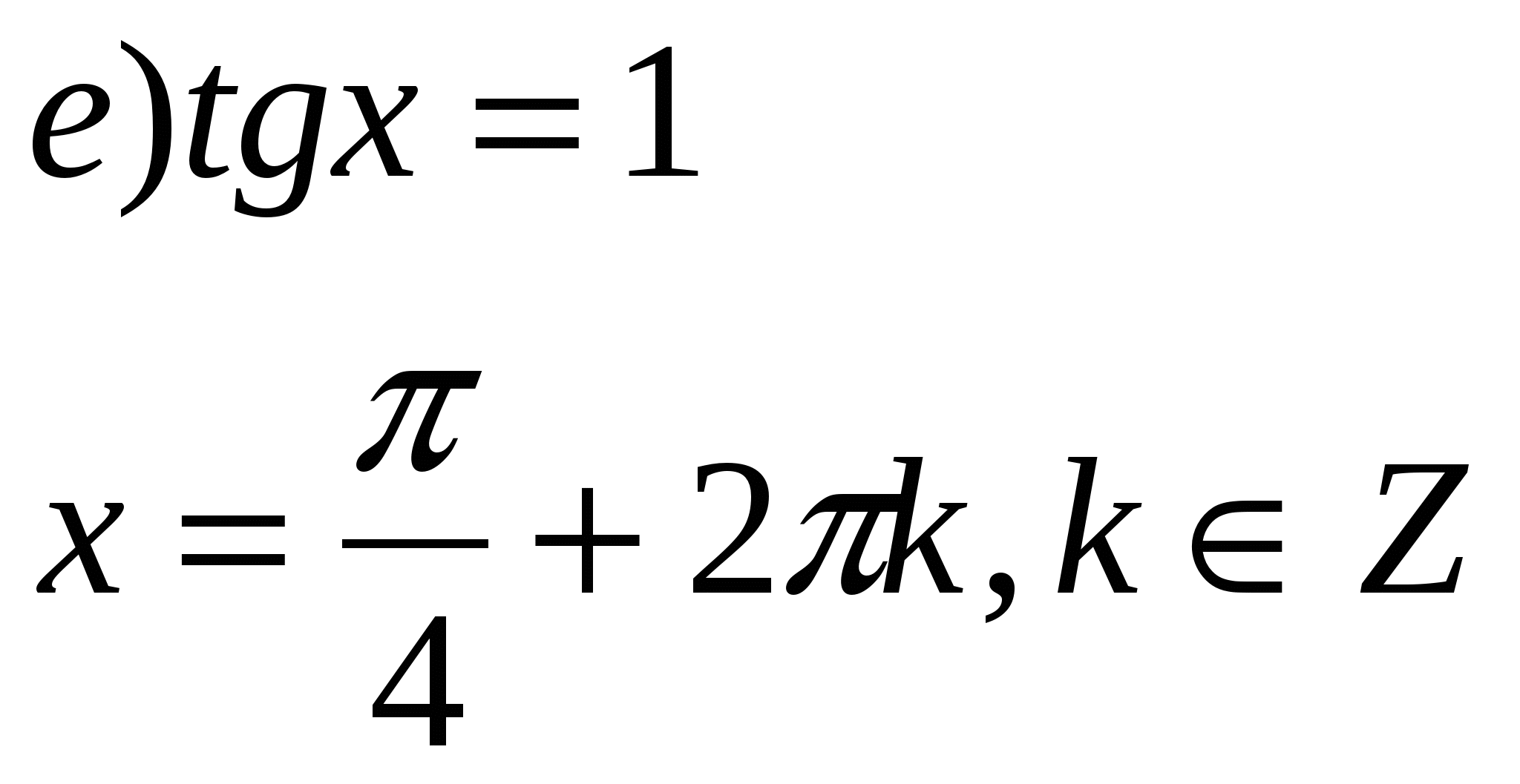
3.Индивидуальная работа. Разгадать фразу, записанную на доске в виде цифр.

КЛЮЧ К РАЗГАДКЕ

Сегодня на уроке мы рассмотрим основные методы решения сложных тригонометрических уравнений.

1. Метод приведение к простейшим тригонометрическим уравнениям.

Сформулируйте алгоритм решения уравнений методом приведения к простейшим тригонометрическим уравнениям:

1. Выразить тригонометрическую функцию через известные компоненты.

2. Найти аргумент функции по формулам:

3. Найти неизвестную переменную.

2. Метод введения новой переменной.

Пример.

2 cos ² x – cos x – 1 = 0

Решение:

t =cos x

2t² – t -1 = 0

D = 9

t_{1 =    1}                                                  t_{2 = 1/2}

_{cos x = 1                                               cos x = 1/2}

Ответ: x=   2πn, n Є Z               x=π/3 +2πn,, n Є Z.

Cформулируйте алгоритм решения уравнений методом введения новой переменной.

1. Привести уравнение к алгебраическому виду относительно одной из тригонометрических функций.

2. Обозначить полученную функцию переменной t .

3. Записать и решить полученное алгебраическое уравнение.

4. Сделать обратную замену.

5. Решить простейшее тригонометрическое уравнение.

3. Метод понижения порядка уравнения.

Формулы понижения степени:

sin² x = 1/2 · (1 – cos 2x);

cos² x = 1/2 · (1 + cos 2x);

tg² x = (1 – cos 2x) / (1 + cos 2x).

Пример.

cos 2x + cos² x = 5/4.

Решение.

1) cos 2x + 1/2 · (1 + cos 2x) = 5/4.

2) cos 2x + 1/2 + 1/2 · cos 2x = 5/4;

3/2 · cos 2x = 3/4;

cos 2x = 1/2;

2x = ±π/3 + 2πn, n Є Z;    

x = ±π/6 + πn, n Є Z.

Ответ:  x = ±π/6 + πn, n Є Z.

Сформулируйте алгоритм решения уравнений методом введения новой переменной.

1. Заменить данное уравнение линейным, используя для этого формулы понижения степени:

2. Решить полученное уравнение с помощью методов I и II.

4. Приведение уравнения к виду  tg x =a

Однородные уравнения.

Пример.

5sin² x + 3sin x · cos x – 4 = 0.

Решение.

1) 5sin² x + 3sin x · cos x – 4(sin² x + cos² x) = 0;

5sin² x + 3sin x · cos x – 4sin² x – 4cos² x = 0;

sin² x + 3sin x · cos x – 4cos² x = 0/cos² x ≠ 0.

2) tg² x + 3tg x – 4 = 0.

3) Пусть tg x = t, тогда

t² + 3t – 4 = 0;

t = 1 или t = -4, значит

tg x = 1 или tg x = -4.

Из первого уравнения x = π/4 + πn, n Є Z; из второго уравнения x = -arctg 4 + πk, k Є Z.

Ответ:  x = π/4 + πn, n Є Z; x = -arctg 4 + πk, k Є Z.

Сформулируйте алгоритм решения уравнений методом приведения к виду

tg x =a

1. Привести данное уравнение к виду

a) a sin x + b cos x = 0 (однородное уравнение первой степени)

или к виду

б) a sin² x + b sin x · cos x + c cos² x = 0 (однородное уравнение второй степени).

 2. Разделить обе части уравнения на

а) cos x ≠ 0;

б) cos² x ≠ 0;

и получить уравнение относительно tg x:

а) a tg x + b = 0;

б) a tg² x + b tg x + c = 0.

 3. Решить уравнение известными способами.

  5. Разложение на множители.    

Алгоритм решения:

 1. Используя всевозможные тригонометрические формулы, привести данное уравнение к уравнению, решаемому методами I, II, III, IV.

 2. Решить полученное уравнение известными методами.

Пример.

sin x + sin 2x + sin 3x = 0.

Решение.

1) (sin x + sin 3x) + sin 2x = 0;

2sin 2x · cos x + sin 2x = 0.

2) sin 2x · (2cos x + 1) = 0;

sin 2x = 0 или 2cos x + 1 = 0;

Из первого уравнения 2x = π/2 + πn, n Є Z; из второго уравнения cos x = -1/2.

Имеем х = π/4 + πn/2, n Є Z; из второго уравнения x = ±(π – π/3) + 2πk, k Є Z.

В итоге х = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.

Ответ:  х = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.

И напоследок притча:

“Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному дверному замку. Кто откроет, тот и будет первым помощником. Никто не притронулся даже к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ.
Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, но надеешься на собственные силы и не боишься сделать попытку.”