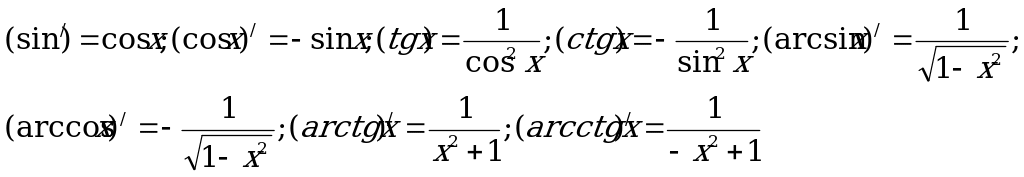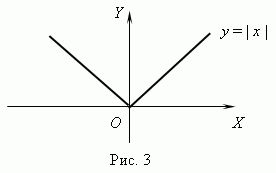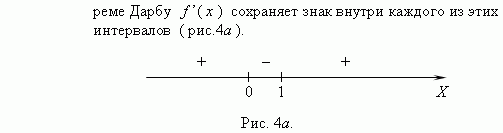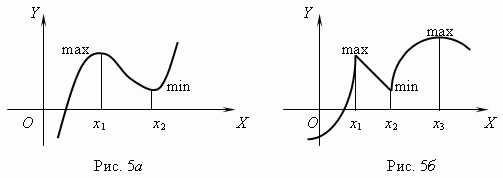Лекционный материал на тему: "Производная функции".

8

Раздел 1. Математический анализ

Лекция №1

Тема: Дифференциальное исчисление. Производная функции, её геометрический и физический смысл, производная сложной и обратной функций.

План:

1. Определение производной, ее геометрический и физический смысл.

2. Непрерывность и дифференцируемость функции.

3. Правила вычисления производных.

4. Таблица производных.

5. Производная обратной функции.

6. Производная сложной функции.

7. Применение производных при исследовании функции и построения графиков.

1.Определение производной, ее геометрический и физический смысл:

Пусть дана функция у=f(x). Разность x-x , называется приращением аргумента и обозначается ∆х= x-x . Разность f(x)-f(x ) называется приращением функции и обозначается ∆у

Определение: Производной у или f(х) от данной функции y=f(x) называется предел отношения приращения функции к вызвавшему его приращению аргумента, при условии, что приращение аргумента стремится к нулю: 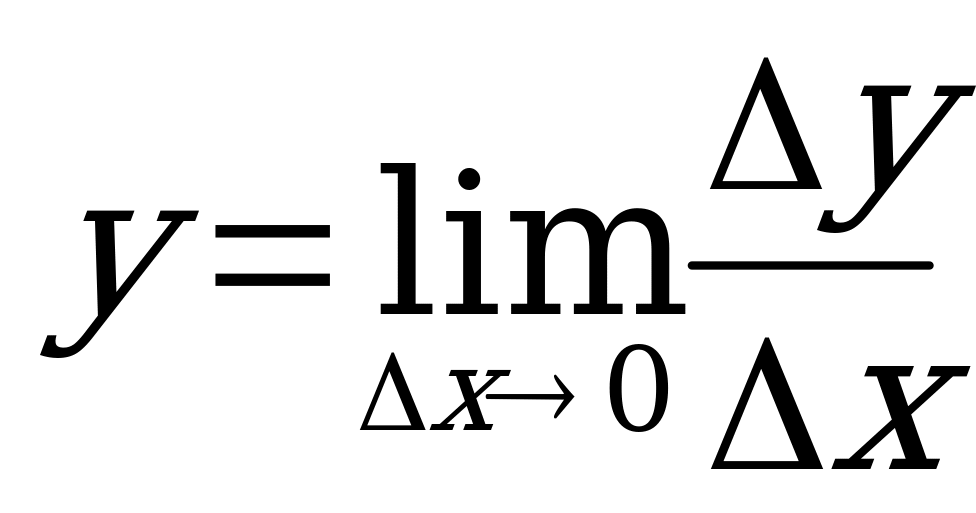. Обозначается производная f (x).

Пример. 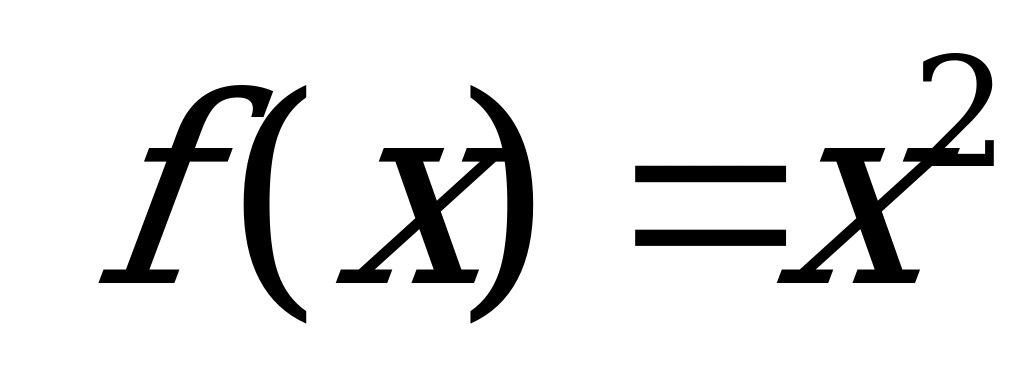, имеем: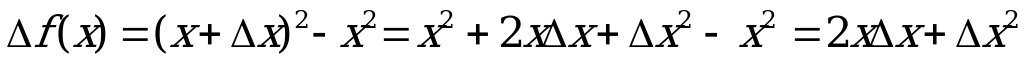

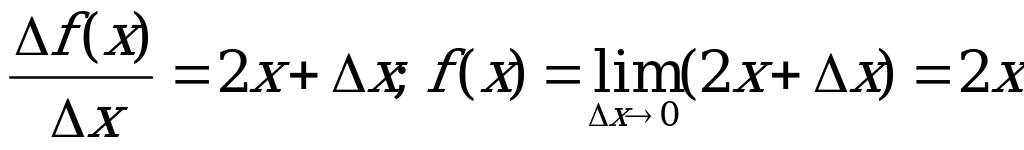
Понятие производной - основное понятие математического анализа. К понятию производной приходится обращаться при решении целого ряда задач физики, механики, геометрии, экономики и ряда других областей.

Выясним геометрический смысл производной. Решим следующую задачу: найдем уравнение касательной к графику функции y=f(x) в произвольной его точке Мо(хо, уо). Касательная к произвольной кривой (графику) в некоторой ее точке М₀ определяется следующим образом: возьмем на кривой соседнюю точку Mi, проведем через точки М₀ и M1 секущую, и будем приближать точку M1 к точке Мо, двигаясь по кривой; предельное положение М₀Т (если оно существует) секущей Мо M1, когда точка М1 сольется с точкой Мо, и определит касательную к данной кривой в точке М₀.

У

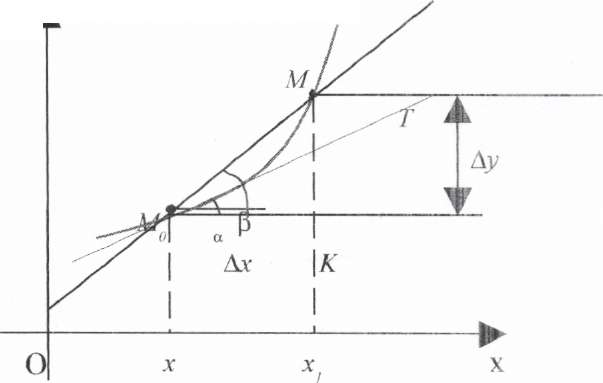
Итак, касательной к данной кривой в некоторой ее точке М₀ называется прямая, являющаяся предельным положением секущей, проходящей через точку М₀ и соседнюю точку кривой М1, при условии, что точка M1, двигаясь по кривой, стремится слиться с точкой М_0.

Итак, точка Мо(хо, yo=f(xo)), точка M .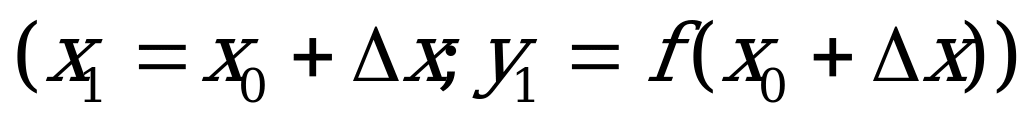

Угловой коэффициент секущей k, равный тангенсу угла 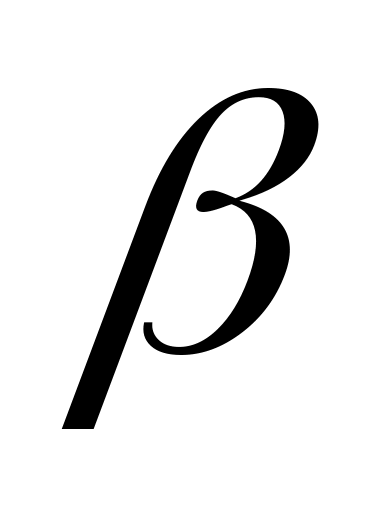ее наклона к оси Ох, определится так:

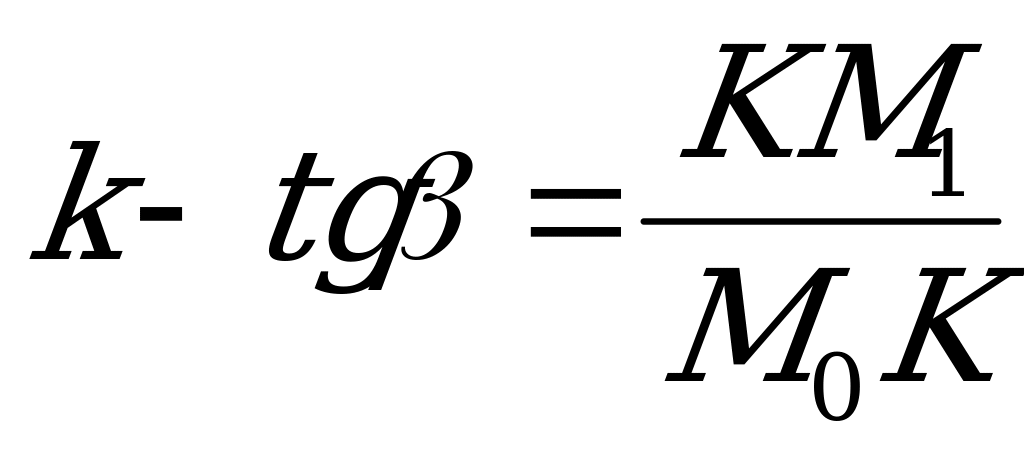Но .

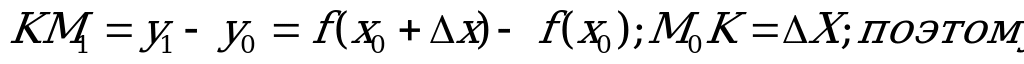
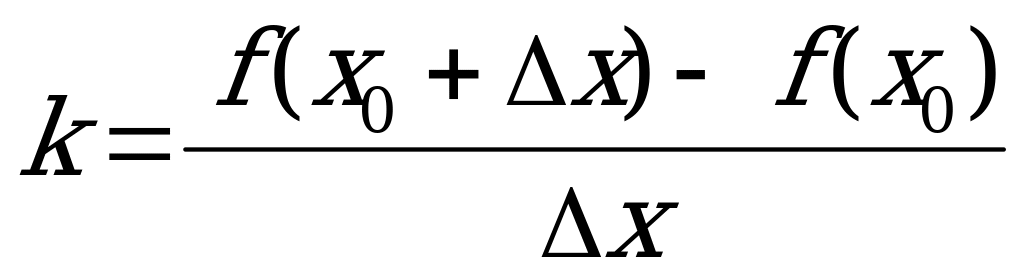Когда точка 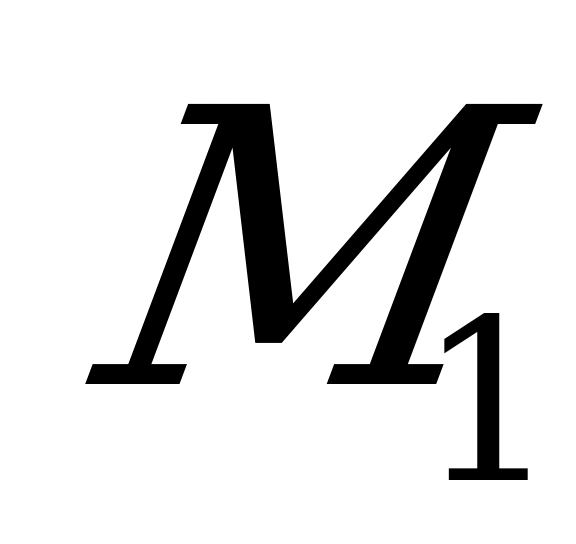стремится к точке 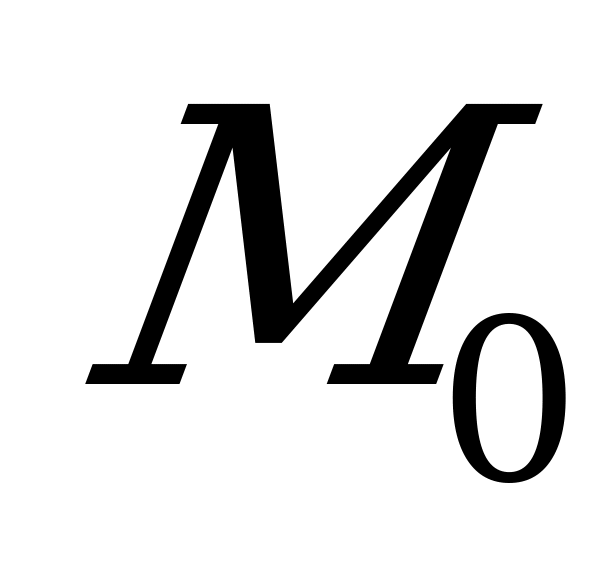, а секущая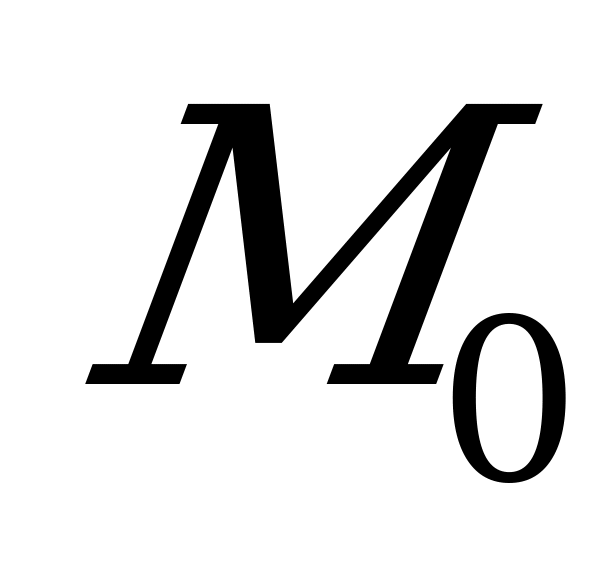 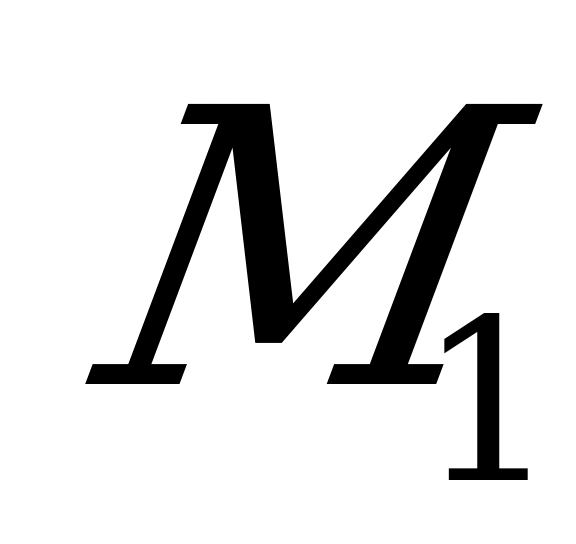, стремится занять положение

касательной М₀Т, то угол 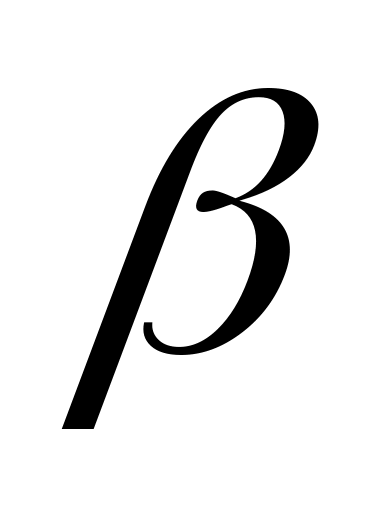наклона секущей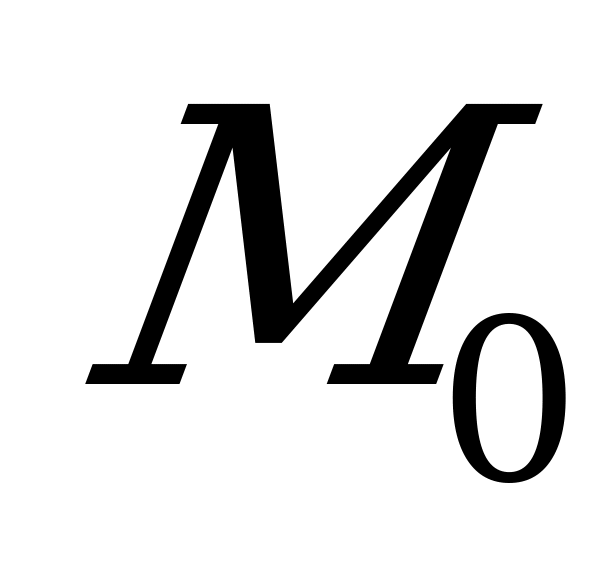 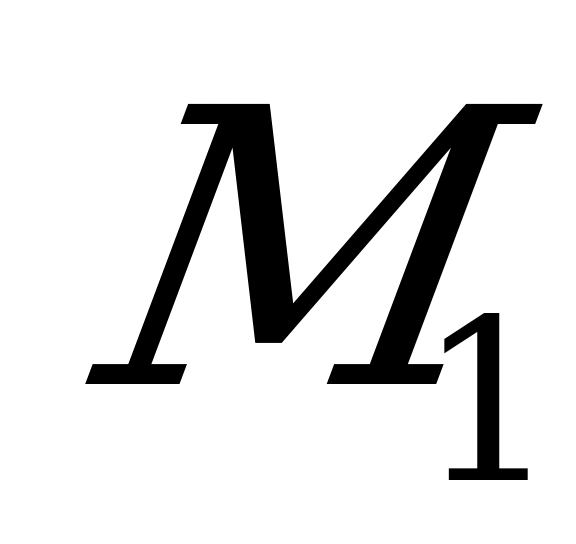к оси Ох стремится к углу (наклона

М₀Т к. оси Ox), a 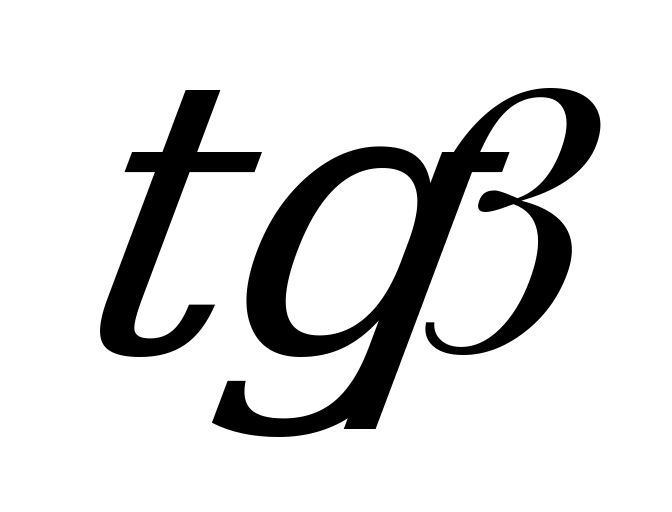стремится к tg (тангенс - функция непрерывная).

Но, когда точка 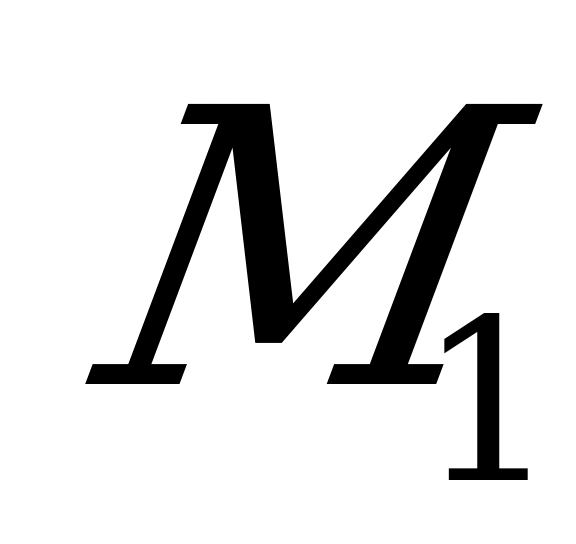, стремится к точке М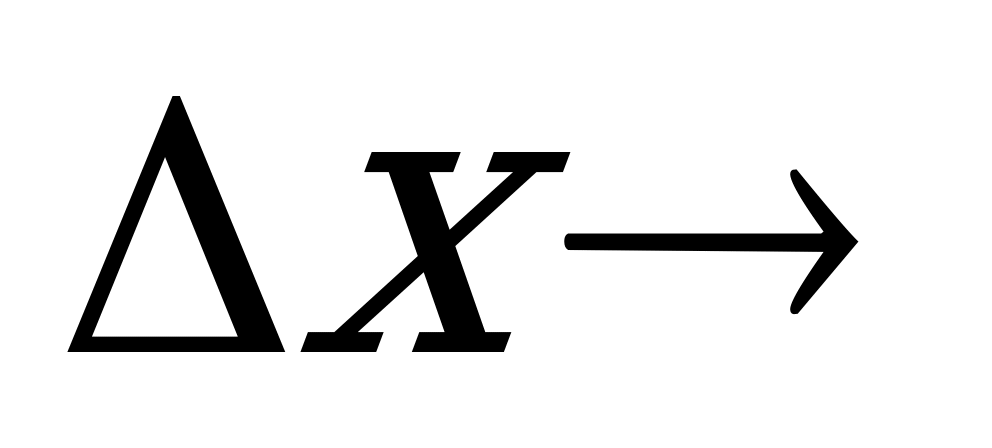₀, 0, 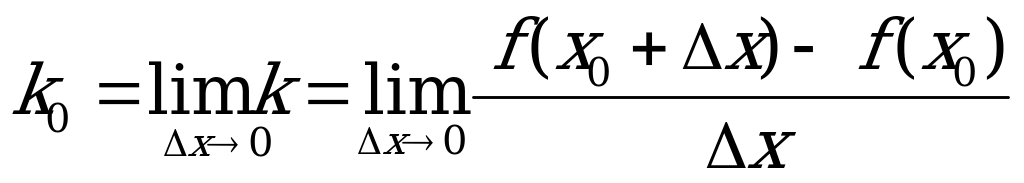или, по определению производной, .

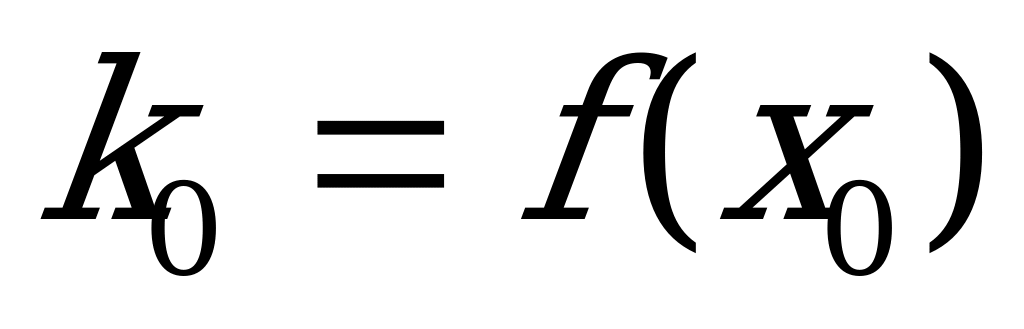Получим теперь уравнение касательной MoT как уравнение прямой, проходящей через заданную точку графика 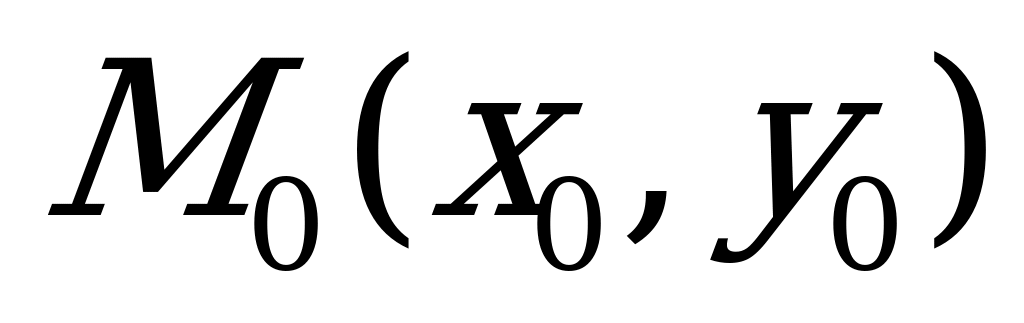, угловой коэффициент которой .

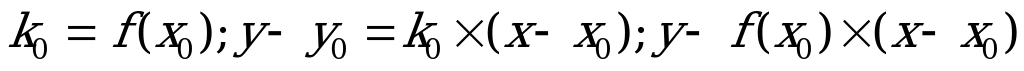Геометрический смысл производной - производная от данной функции 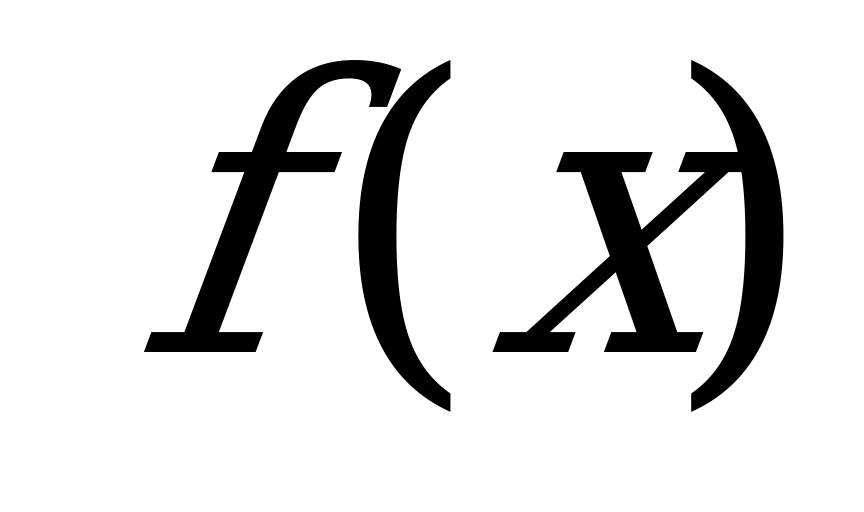при данном значении 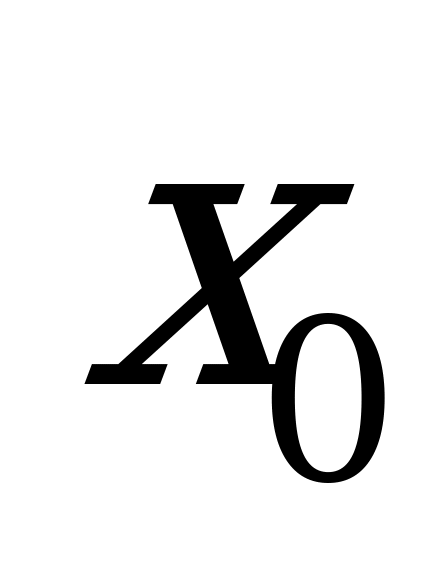аргумента равна угловому коэффициенту касательной к графику этой функции в соответствующей точке 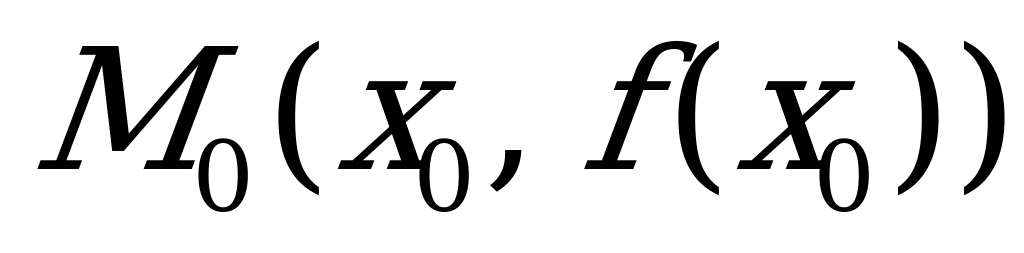. Отсюда следует, что f (x)=R=tgα.

Физический смысл производной заключается в том, что производная от пути по времени есть скорость.

V=S (t)

Производная функции у = 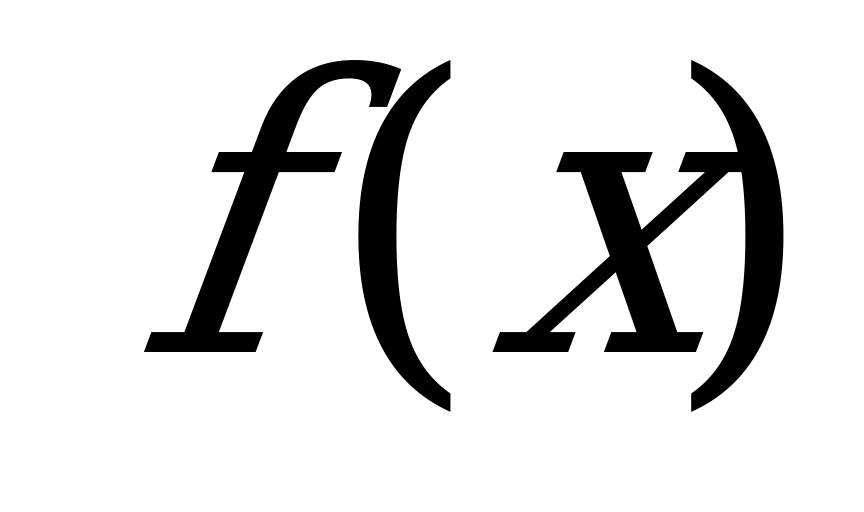в точке х выражает скорость изменения функции в точке х, т. е. скорость протекания процесса, описываемого зависимостью у = .

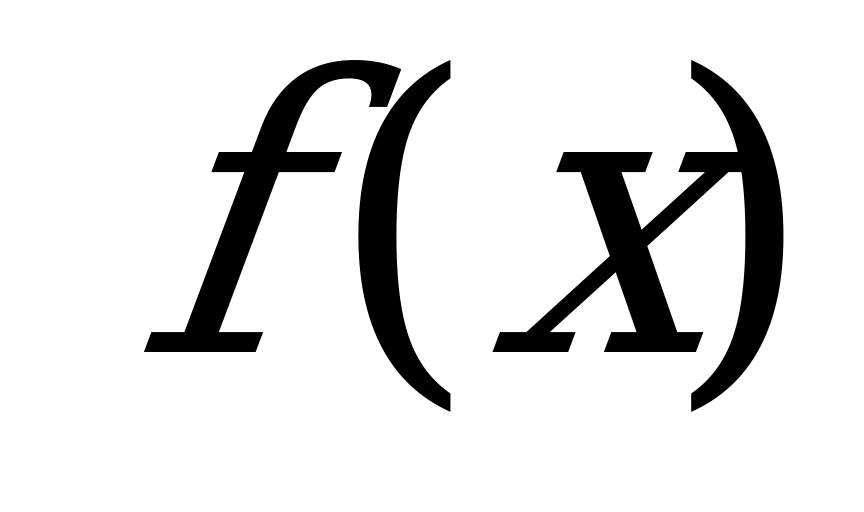Процесс нахождения производной функции называется дифференцированием.

2.Непрерывность и дифференцируемость функции:

Итак,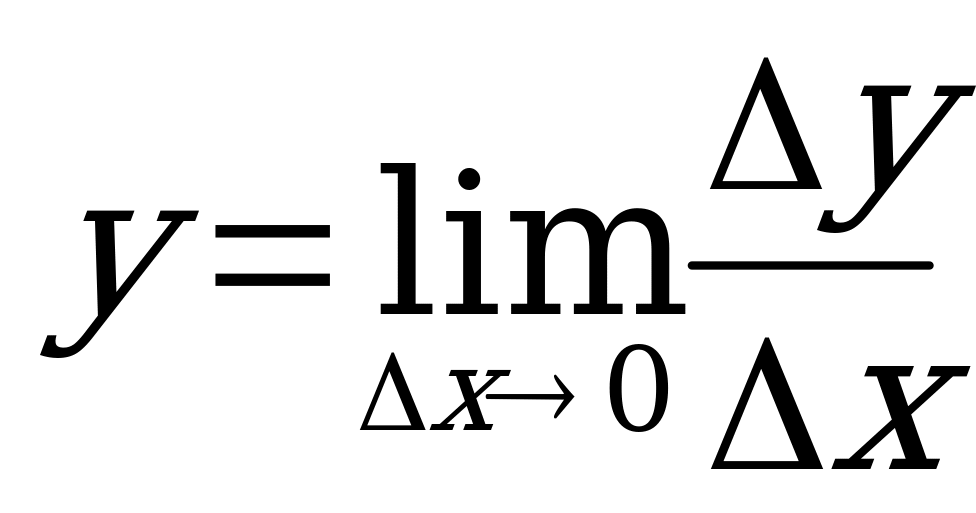

Но этот предел существует не для всякой функции, а если и существует, то не обязательно при всех значениях ее аргумента, при которых функция определена.

Определение. Функция, имеющая в данной точке 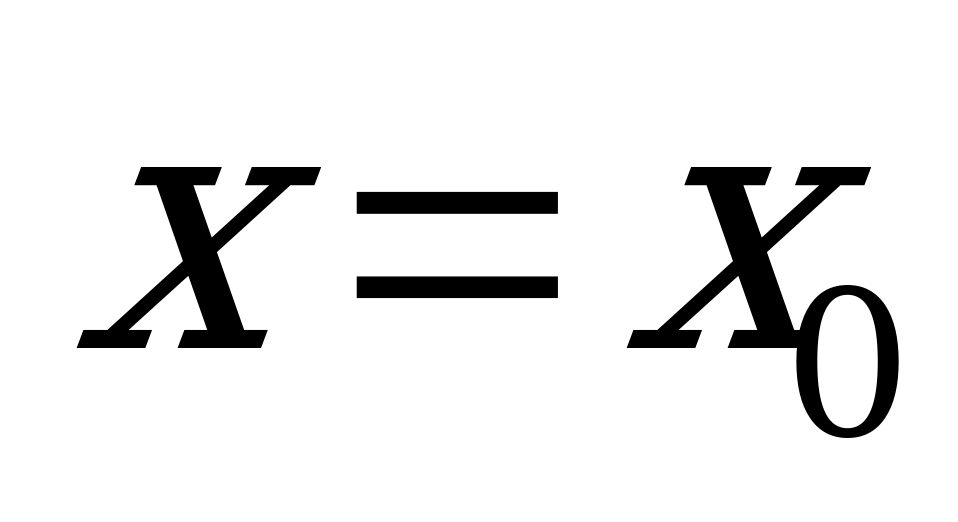производную, называется дифференцируемой в этой точке.

Определение. Функция, имеющая производную во всех точках интервала (а, Ь), называется дифференцируемой в этом интервале.

Теорема. Если функция y=f(x) дифференцируема в точке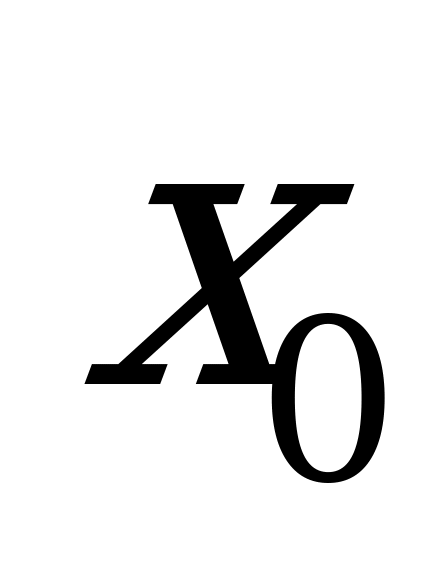 , то она в этой точке непрерывна.

Доказательство. Пусть аргумент х получает в точке хо приращение 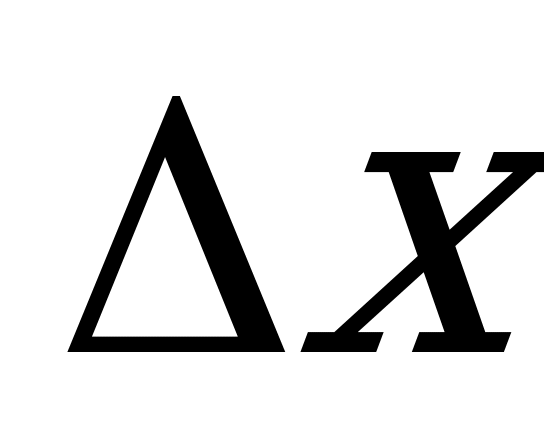не равное нулю. Ему соответствует приращение функции . Рассмотрим очевидное тождество:

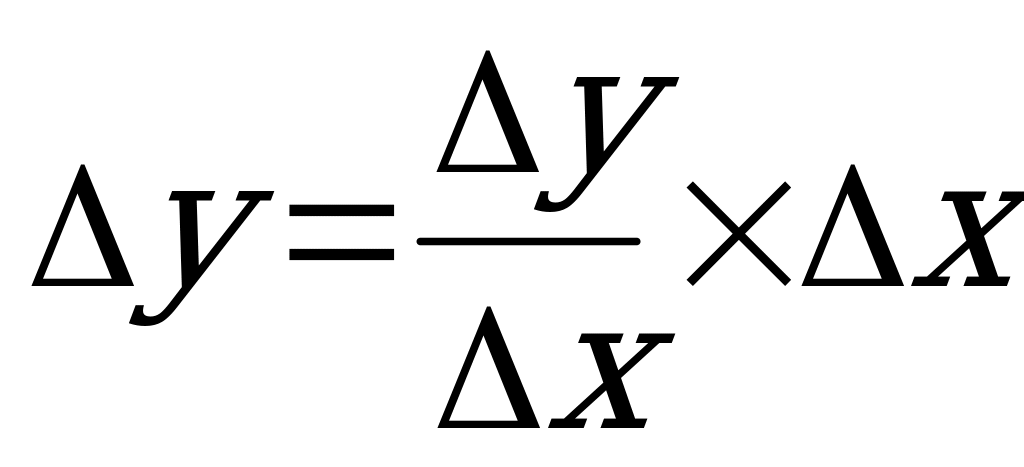. Перейдем к пределу: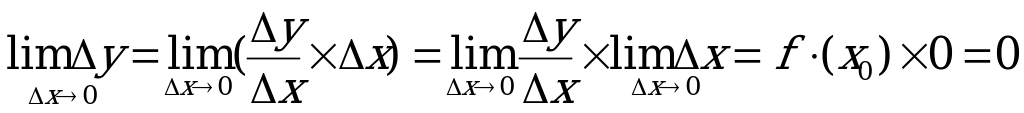

откуда и следует непрерывность функции в точке х₀ (функция непрерывна, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции). Итак, необходимым условием дифференцируемости функции является ее непрерывность, то есть всякая дифференцируемая функция непрерывна. Обратное - неверно: не всякая непрерывная функция дифференцируема.

Пример: 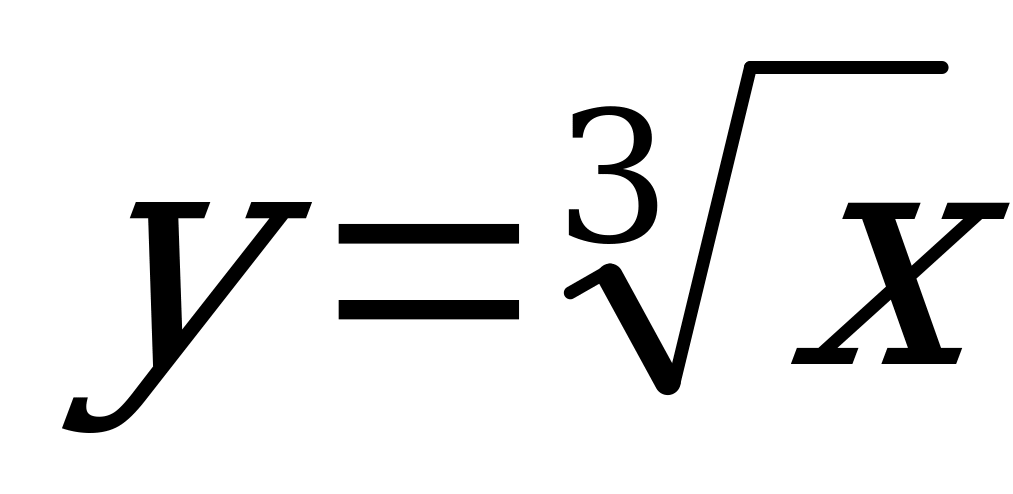; функция непрерывна на всей числовой оси, но в точке х=0 не имеет производной.

.

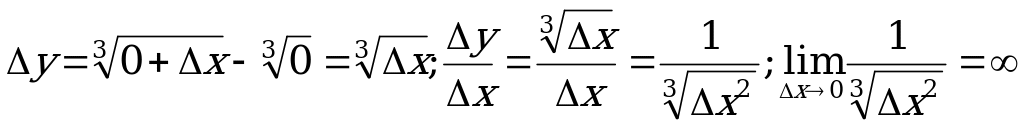3. Правила вычисления производных:

1. Производная постоянной равна нулю (С) =0

1. Если функции U и V дифференцируемы, то их сумма и разность дифференцируемы по правилу: (U+V) = U + V ; (U-V) = U - V ;

1. Если функции U и V дифференцируемы, то их произведение дифференцируемо по правилу: (UV) = U V+UV .

1. Если функции U и V дифференцируемы и функция V не равна нулю, то частное 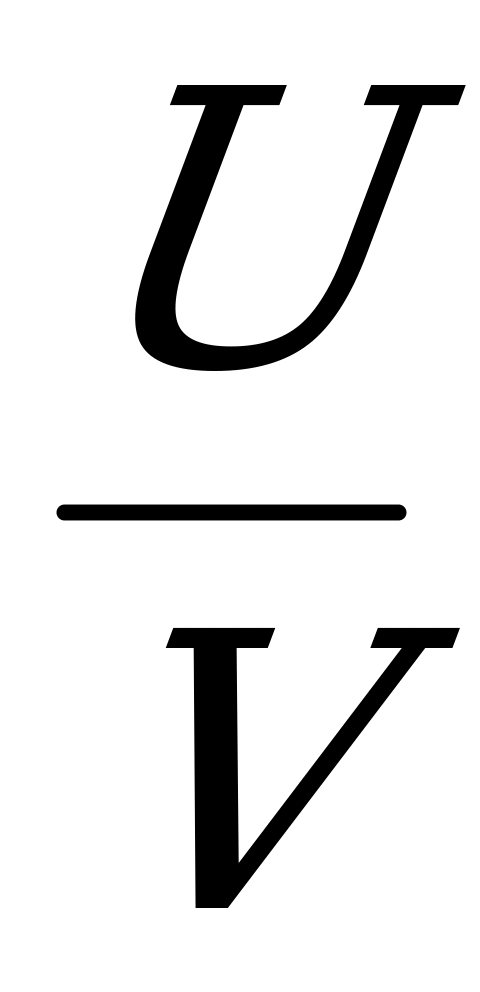дифференцируемо по правилу: ( ) = .

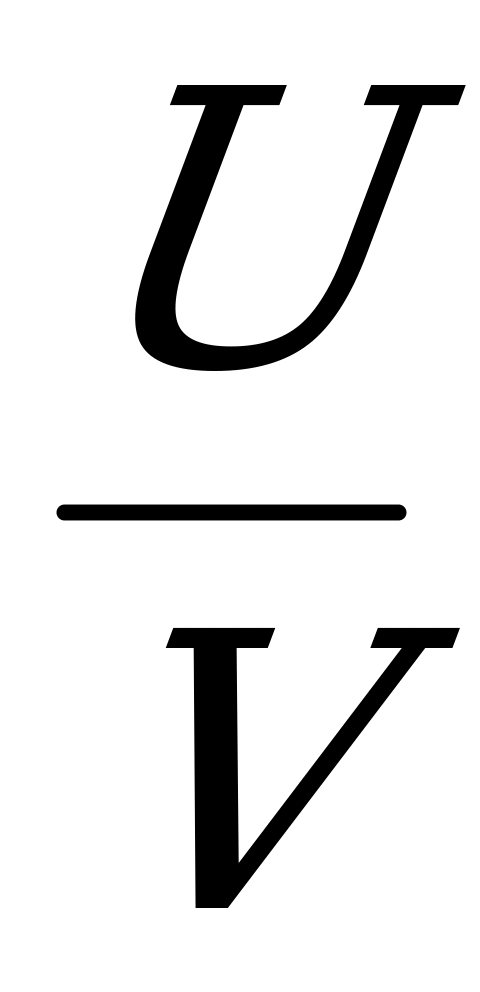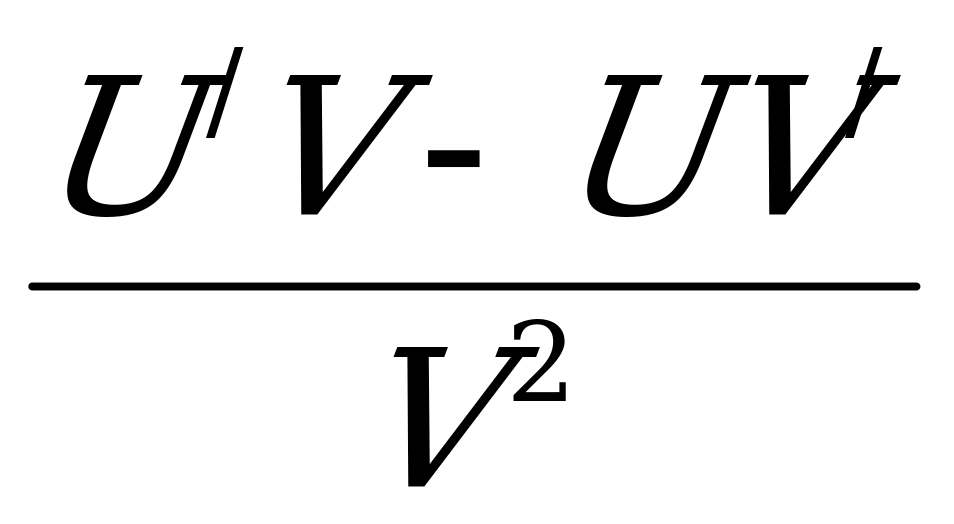1. Постоянный множитель выносят за знак производной: (С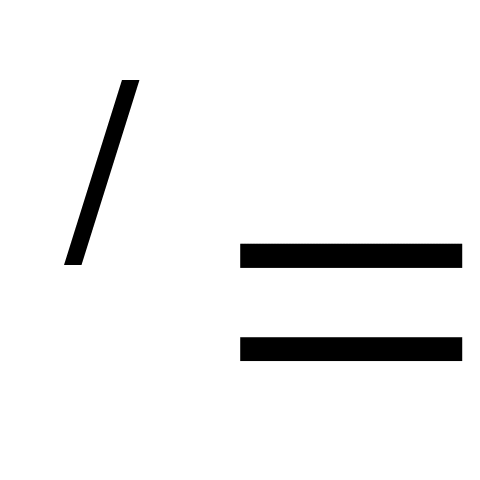U) CU

4.Таблица производных основных функций.

1. Производная степенной функции 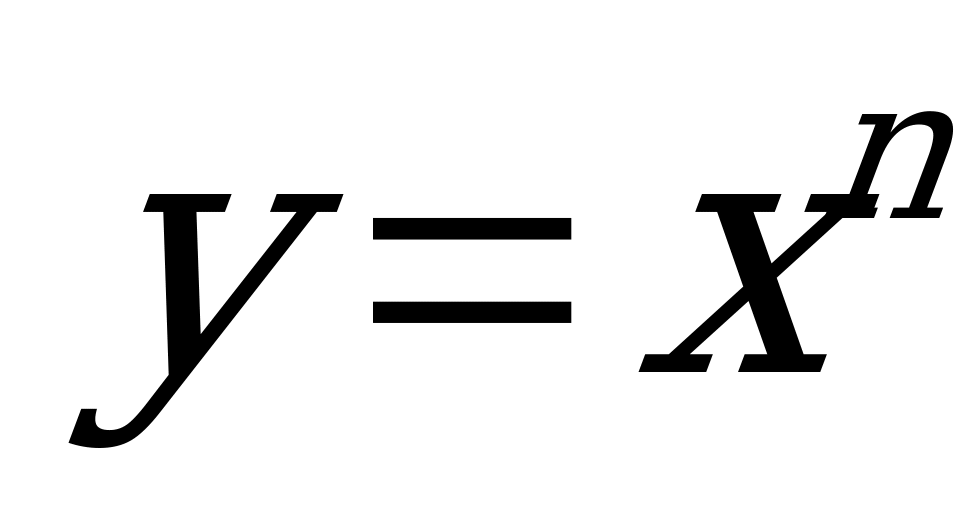с натуральным показателем .

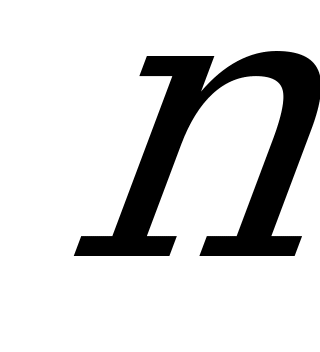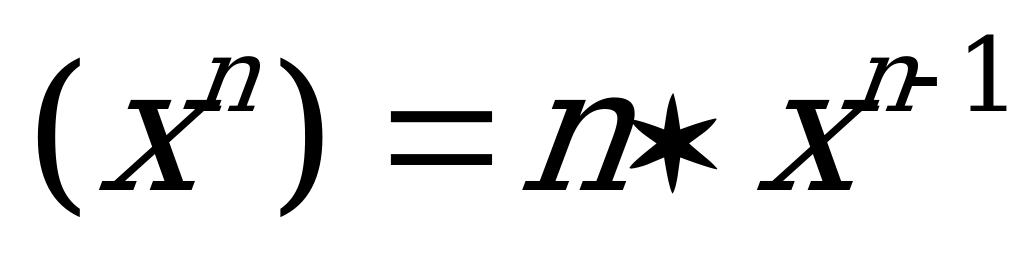
2. Производная показательной функции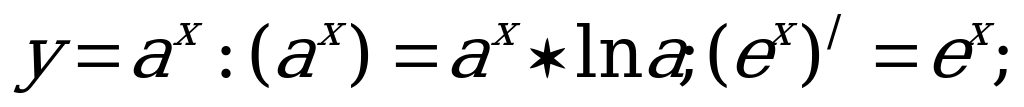

3. Производная логарифмической функции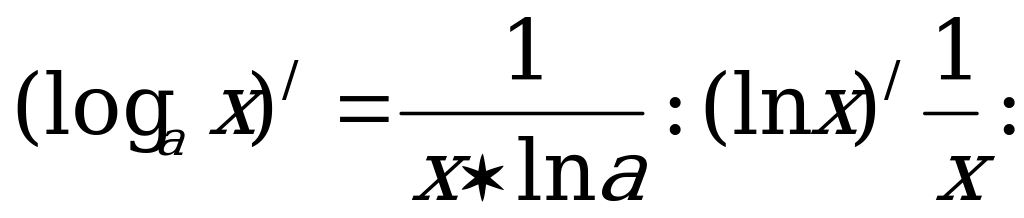

4. Производные тригонометрических и обратных тригонометрических функций: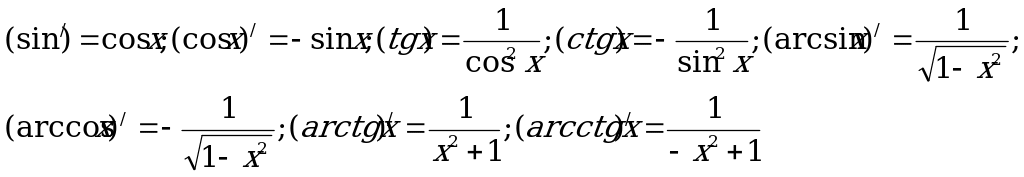

5.Производная обратной функции:

Определение: Пусть X и Y – некоторые множества и пусть задана функция f, т.е. множество пар чисел (х;у) (х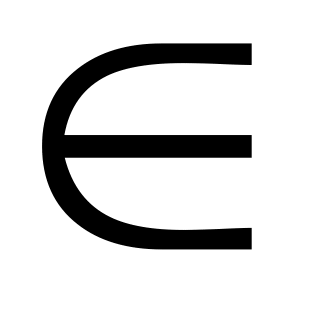 Х; у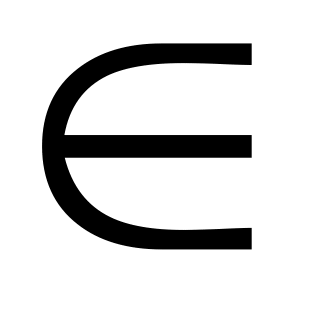 Y). Если в этом множестве х и у поменять местами, то получим множество (у;х), которое называется обратной функцией h к функции f

Обратную функцию будем обозначать символом х = h(у).

Из определения следует, что если обратная функция однозначна, то множество значений У функции f является областью определения обратной функции h, а область определения Х функции f – множеством значений обратной функции h.

Теорема1: Если функция У= f(x) определена, строго монотонна и непрерывна на некотором промежутке Х и пусть У – множество ее значений, то на множестве У обратная функция h(x) однозначна, строго монотонна и непрерывна.

Теорема2: Если функция у=f(x) имеет в точке х производную 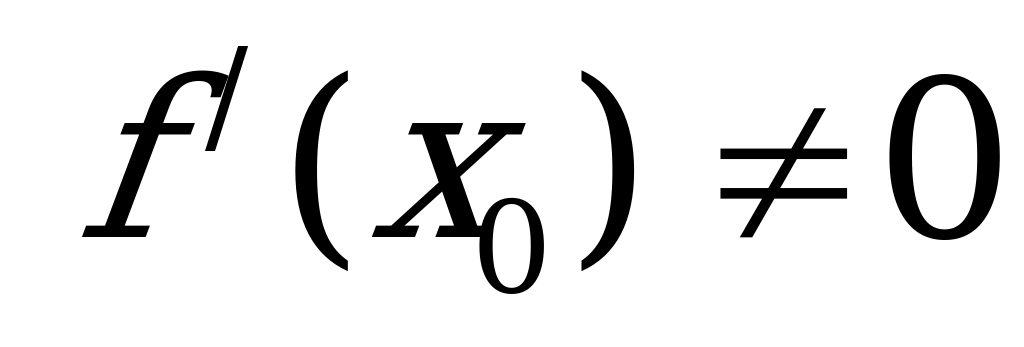, то обратная функция х = h(у) также имеет в соответствующей точке у = производную, причем

h =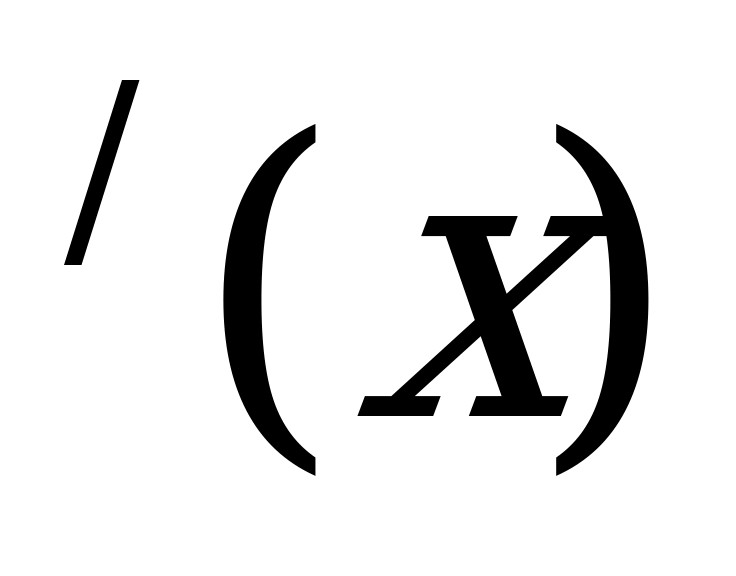

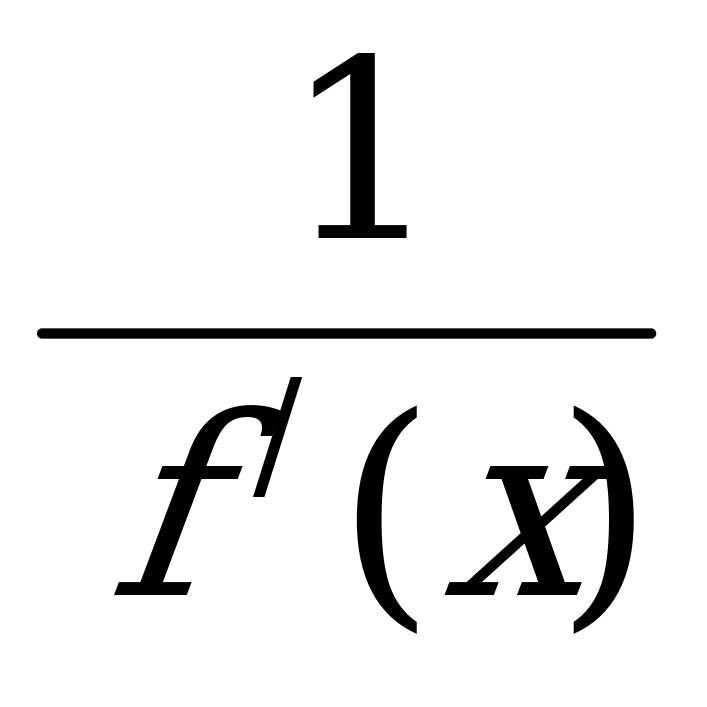
6.Производная сложной функции:

Определение: Если на некотором промежутке x определена функция у= f(u) с множеством значений у, а на множестве у определена функция у = u(x), то функция у = f(u(x)) называется сложной функцией.

Производная сложной функции вычисляется по формуле:

y =f (u(x))u (x).

Пример:

Вычислить производную функции у=( 2х+5)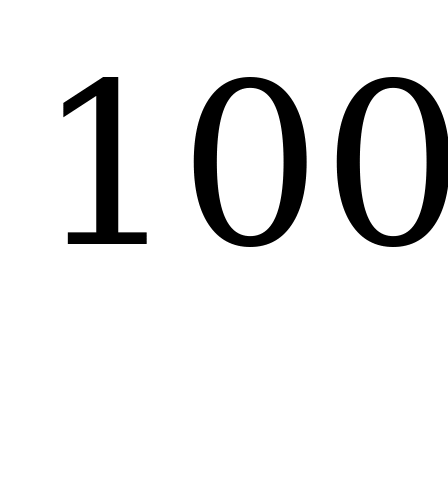 , данная функция является сложной.

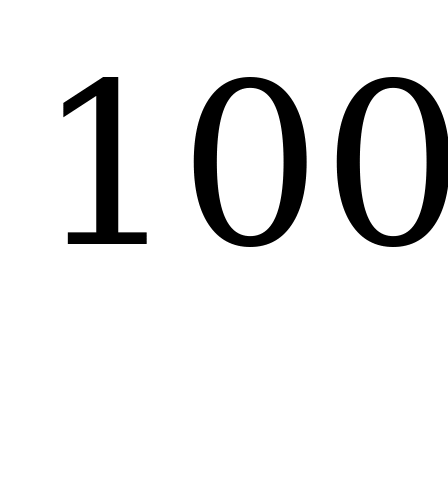у =(2х+5) ) =100(2х+5) (2х+5) = 200((2х+5)

7. Применение производных при исследовании функции и построения графиков.

Связь между непрерывностью и дифференцируемостью функции. Если функция f ( x ) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной.

С л е д с т в и е . Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.

П р и м е р .

Функция y = | x | ( рис.3 ) всюду непрерывна, но она не имеет производной при x = 0 , так как в этой точке не существует касательной к графику этой функции.

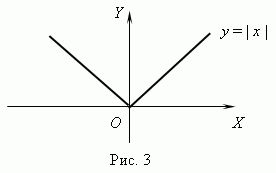
Достаточные признаки монотонности функции.

Если f ’( x ) 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.

Если f ’( x )

Теорема Дарбу: Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.

Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.

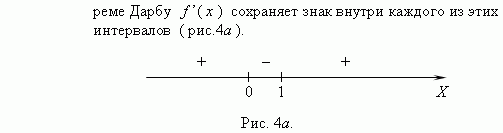
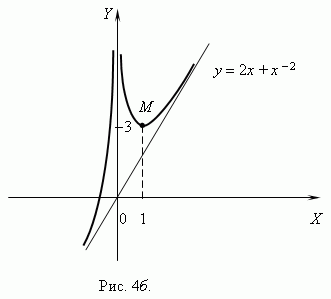
Следовательно, функция возрастает на интервалах ( - , 0 ) и ( 1, + ) и убывает на интервале ( 0, 1 ). Точка x = 0 не входит в область определения функции, но по мере приближения x к 0 слагаемое x - 2 неограниченно возрастает, поэтому функция также неограниченно возрастает. В точке x = 1 значение функции равно 3. В соответствии с этим анализом мы можем построить график функции ( рис.4б ) .

Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум ( минимум или максимум , рис.5а,б).

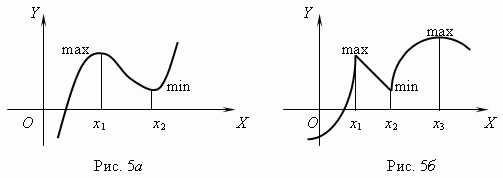
В точках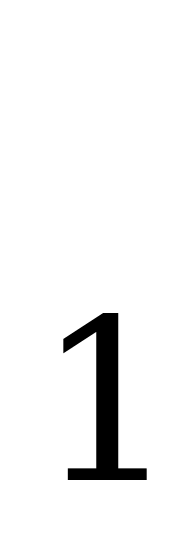 x , x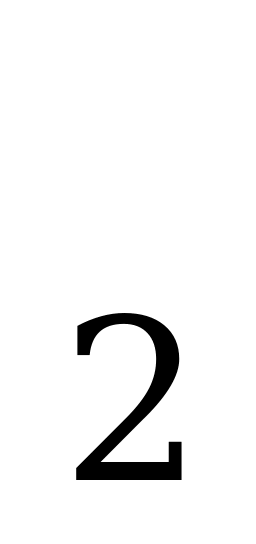 ( рис.5a ) и x 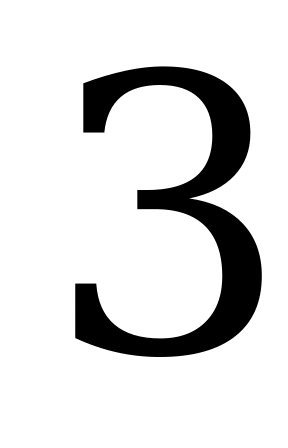( рис.5b ) производная равна 0; в точка 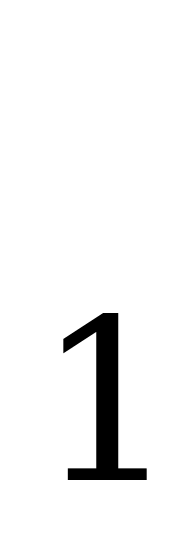x x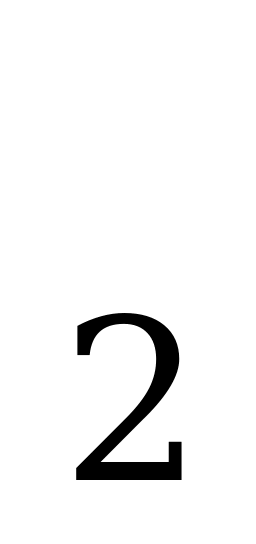 ( рис.5б ) производная не существует. Но все они точки экстремума.

Необходимое условие экстремума. Если x - точка экстремума функции f ( x ) и производная f’ существует в этой точке, то f’ (x ) = 0.

Эта теорема - необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке. Например, производная функции f ( x ) = x 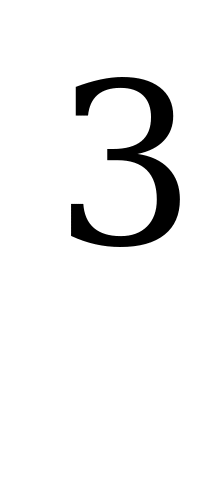равна 0 при x = 0, но эта функция не имеет экстремум в этой точке ( рис.6)

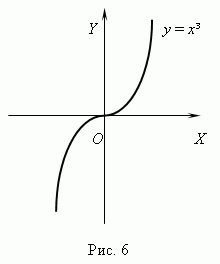
Достаточные условия экстремума.

Если производная при переходе через точку x меняет свой знак с плюса на минус, то x - точка максимума.

Если производная при переходе через точку x меняет свой знак с минуса на плюс, то x - точка минимума.

План исследования функции.

Для построения графика функции нужно:

1) найти область определения и область значений функции,

2) установить, является ли функция чётной или нечётной,

3) определить, является ли функция периодической или нет,

4) найти нули функции и её значения при x = 0,

5) найти интервалы знакопостоянства,

6) найти интервалы монотонности,

7) найти точки экстремума и значения функции в этих точках,

8) проанализировать поведение функции вблизи “особых” точек

и при больших значениях модуля x .
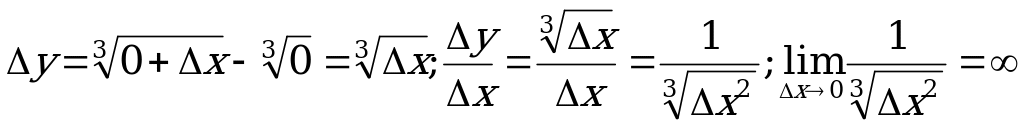