Дистанционный курс по математике для студентов 1 курса
Преподаватель: Добрынина Н.В.
Лекция № 4
Тема: Классическая вероятность. Геометрическая вероятность. Статистическая вероятность.
Цели лекции:
Ввести определения классической, геометрической и статистической вероятности;
Формировать навыки нахождения классической, геометрической и статистической вероятности.
Если результат опыта сводится к схеме случаев (шансов), то отношение числа благоприятных случаев данному событию к числу всех случаев называется вероятностью события.
Р – вероятность.
А – событие.
Р(А) – вероятность события А.
Такое понятие вероятности будем называть классической вероятностью. Формула классической вероятности имеет вид:
Р(А) = 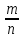 ,
,
где m – число благоприятных случаев, а n – число всех случаев.
Рассмотрим задачи:
Задача 1. Найти вероятность выпадения решки при 1 подбрасывании 1 математической монеты.
Решение:
Е – 1 подбрасывание 1 математической монеты.
А – появление решки.
Р(А) = ½ = 0,5.
Ответ: 0,5.
Задача 2: найти вероятность появление более 3 очков при одном подбрасывании 1 игральной кости.
Решение:
Е – 1 подбрасывание 1 игральной кости.
А – появление более 3 очков.
Р(А) = 3/6 = 0,5.
Ответ: 0,5.
Задача 3: найти вероятность появление орла и решки при одном подбрасывании 2 математических монет.
Решение:
Е – одно подбрасывание 2 математических монет.
А – выпадение орла и решки.
Р(А) = 2/4= 0,5.
Ответ: 0,5.
Если вероятность события А Р(А)=0, то событие А называют невозможным.
Если вероятность события А Р(А)=1, то событие А называют достоверным.
Значение вероятности всегда принадлежит отрезку от 0 до 1.
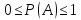
Пусть произведено n опытов, в которых событие А появилось ровно m раз. Тогда отношение 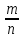 называется частотой появления события А и обозначается Р*(А) =
называется частотой появления события А и обозначается Р*(А) = 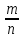 .
.
Число, возле которого колеблется частота появления события А при неограниченном увеличении числа опытов и сохранении тех же условий, называется статистической вероятностью события А.
Рассмотрим задачу.
Задача 4: произведено исследование 100 деталей, среди которых обнаружено 5 бракованных. Какова частота появления бракованной детали?
Решение:
Е – исследование 100 деталей.
А – появление бракованной детали.
Р*(А) = 5/100 = 0,05
Ответ: 0,05.
Отличие от классической вероятности состоит в том, что в статистической вероятности расчет производится после опыта, а в классической теоретически перед опытом.
Рассмотрим несколько задач.
В урне находится 15 белых, 5 красных и 10 чёрных шаров. Наугад извлекается 1 шар, найти вероятность того, что он будет: а) белым, б) красным, в) чёрным.
Решение:
Е – извлечение 1 шара из урны.
А – шар белый.
В – шар красный.
С – шар черный.
Важнейшей предпосылкой для использования классического определения вероятности является возможность подсчёта общего количества исходов.
Всего в урне: 15 + 5 + 10 = 30 шаров, и, очевидно, справедливы следующие факты: извлечение любого шара одинаково возможно (равно возможность исходов), при этом исходы элементарны и образуют полную группу событий (т.е. в результате испытания обязательно будет извлечён какой-то один из 30-ти шаров).
Таким образом, общее число исходов: 30.
Рассмотрим событие: А – из урны будет извлечён белый шар. Данному событию благоприятствуют 15 элементарных исходов, поэтому по классическому определению:
Р(А) = 15/30 = 0,5 вероятность того, то из урны будет извлечён белый шар.
С другими пунктами аналогично, рассмотрим следующие события:
Событию В благоприятствует 5 элементарных исходов, а событию С – 10 элементарных исходов. Таким образом, соответствующие вероятности:
Р (В) = 5/30 =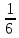 – из урны будет извлечён красный шар;
– из урны будет извлечён красный шар;
Р(С) = 10/30 = 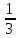 – из урны будет извлечён чёрный шар.
– из урны будет извлечён чёрный шар.
Ответ: 0,5; 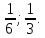
В магазин поступило 30 холодильников, пять из которых имеют заводской дефект. Случайным образом выбирают один холодильник. Какова вероятность того, что он будет без дефекта?
Решение:
Е – выбор одного холодильника.
А – выбранный холодильник без дефекта.
Количество всех исходов в задаче равно 30. Благоприятные исходы можно найти 30 – 5 = 25. Получим вероятность события А:
Р (А) = 25/30= 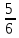
Ответ: 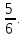
Набирая номер телефона, абонент забыл две последние цифры, но помнит, что одна из них – ноль, а другая – нечётная. Найти вероятность того, что он наберёт правильный номер.
Решение:
Е – набор номера.
А – номер набран правильно.
Примечание: ноль – это чётное число (делится на 2 без остатка)
Сначала найдём общее количество исходов. По условию, абонент помнит, что одна из цифр – ноль, а другая цифра – нечётная.
01, 03, 05, 07, 09
10, 30, 50, 70, 90
Подсчитываем их – всего: 10 исходов.
Благоприятствующий исход один: верный номер. По классическому определению:
Р(А) = 1/10 = 0,1 – вероятность того, что абонент наберёт правильный номер.
Ответ: 0,1.
Абонент забыл пин – код к своей сим-карте, однако помнит, что он содержит три «пятёрки», а одна из цифр – то ли «семёрка», то ли «восьмёрка». Какова вероятность успешной авторизации с первой попытки?
Решение:
Е – набор пин-кода.
А – пин-код набран верно.
Количество всех исходов равно 8.
5557
5558
5575
5585
5755
5855
7555
8555
Благоприятных исход 1 – верный пин-код.
По классическому определению вероятности имеем:
Р(А) = 1/8 = 0,125.
Ответ: 0,125.
Найти вероятность того, что при бросании двух игральных костей в сумме выпадет:
а) пять очков;
б) не более четырёх очков;
в) от 3-х до 9 очков включительно.
Решение:
Е – подбрасывание 2 игральных костей.
А – сумма очков равна 5.
В – сумма очков не более 4.
С – сумма очков от 3 до 9.
Найдём общее количество исходов: 6 способами может выпасть грань 1-го кубика и 6 способами может выпасть грань 2-го кубика; по правилу умножения комбинаций, всего: 6*6 = 36 возможных комбинаций.
Иными словами, каждая грань 1-го кубика может составить упорядоченную пару с каждой гранью 2-го кубика. Например:
– на первом кубике выпало 3 очка, на втором – 5 очков, сумма очков: 3 + 5 = 8;
– на первом кубике выпало 6 очков, на втором – 1 очко, сумма очков: 6 + 1 = 7;
– на обеих костях выпало 2 очка, сумма: 2 + 2 = 4.
Очевидно, что наименьшую сумму даёт пара 1+1 , а наибольшую – две «шестёрки».
а) Рассмотрим событие: А – при бросании двух игральных костей выпадет 5 очков. Запишем и подсчитаем количество исходов, которые благоприятствуют данному событию:
1+4, 4+1, 3+2, 2+3
Итого: 4 благоприятствующих исхода. По классическому определению:
Р(А) = 4/36= 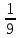 – искомая вероятность.
– искомая вероятность.
б) Рассмотрим событие: В – выпадет не более 4-х очков. То есть, либо 2, либо 3, либо 4 очка.
1+1, 1+2, 2+1, 2+2, 1+3, 3+1
Итого: 6 благоприятствующих комбинаций. Таким образом, Р(В) = 6/36 = 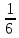 – вероятность того, что выпадет не более 4-х очков.
– вероятность того, что выпадет не более 4-х очков.
в) Рассмотрим событие: С – выпадет от 3-х до 9 очков включительно. Можно исключить выпадение 2, 10, 11, 12 очков.
1+1, 4+6, 6+4, 5+5, 6+5, 5+6, 6+6. Итого: 7 неблагоприятных исходов. Т.е. благоприятных исходов 36 – 7 = 29. По классическому определению: Р(С) = 29/36 = 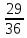 – вероятность того, что выпадет от трёх или до 9-ти очков.
– вероятность того, что выпадет от трёх или до 9-ти очков.
Ответ: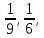
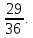
Найти вероятность того, что при броске двух игральных костей произведение очков:
а) будет равно семи;
б) окажется не менее 20-ти;
в) будет чётным.
Решение:
Е – подбрасывание двух игральных костей.
А – произведение очков равно 7.
В – произведение очков не менее 20.
С – произведение очков четно.
Р(А) = 0
Р(В) = 7/35 = 0,5
Р(С) = 26/30 = 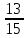
Ответ: 0; 0,5; 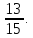
В лифт 20-этажного дома на первом этаже зашли 3 человека. И поехали. Найти вероятность того, что:
а) они выйдут на разных этажах;
б) двое выйдут на одном этаже;
в) все выйдут на одном этаже.
Решение:
Е – выход пассажиров из лифта.
А – все выйдут на разных остановках.
В – двое выйдут на одном этаже.
С – все выйдут на 1 этаже.
Вычислим общее количество исходов: 19 способами может выйти из лифта 1-й пассажир и 19 способами – 2-й пассажир и 19 способами – третий пассажир. По правилу умножения комбинаций: 19*19*19= 6859 возможных исходов. То есть, каждый этаж выхода 1-го человека может комбинироваться с каждым этажом выхода 2-го человека и с каждым этажом выхода 3-го человека.
а) Рассмотрим событие: А – пассажиры выйдут на разных этажах. Вычислим количество благоприятствующих исходов:
17*18*19 = 5814 способами могут выйти 3 пассажира на разных этажах. По классическому определению:
Р(А) = 5814/6859= 0,8476….
в) Рассмотрим событие: С – пассажиры выйдут на одном этаже. Данному событию благоприятствуют 19 исходов и по классическому определению, соответствующая вероятность: Р(С) = 19/6859=0,0028..
б) Рассмотрим событие: В – два человека выйдут на одном этаже (и, соответственно, третий – на другом). Благоприятных исходов 6859 – 19 = 6840. В результате, искомая вероятность: Р(В) = 6840/6859 = 0,1496…
Ответ: 0,8476; 0, 1496; 0,0028.
Когда получаются большие дроби, то хорошим тоном будет указать их приближенные десятичные значения. Обычно округляют до 2-3-4-х знаков после запятой. Иногда по причине погрешности округлений может получиться 0,9999 либо 1,0001, в этом случае одно из приближенных значений следуют «подогнать» так, чтобы в сумме нарисовалась «чистая» единица.
Заметим, что число исходов может быть бесконечным, тогда случайное событие удобнее рассматривать как произвольную точку и говорить о появлении этой точки в некоторой области.
Если возможность случайного появления точки в некоторой области не зависит от положения этой области в пространстве, а зависит лишь от размеров этой области (длина, площадь, объем), то вероятность появления точки определяется как отношение размера этой области к размеру всей области , в которой может появиться данная точка.
Р(А) = 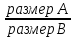 - геометрическое определение вероятности.
- геометрическое определение вероятности.
Рассмотрим примеры.
Задача 12. Абонент ждет телефонного вызова с 2 до 3 часов, то какова вероятность того, что этот вызов пройдет с 2ч 30мин до 2ч 40мин.?
Решение:
Е – ожидание вызова.
D – вызов произошел в течение 10мин после половины третьего.
Изобразим все исходы испытания в виде отрезка ОА на прямой Ох:
![]()
![]()

Событие D произойдет, если точка (вызов) окажется на отрезке СВ.
Следовательно, Р(D) = СВ /ОА= 10/60 = 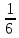
Ответ: 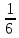
Задача 13. На бесконечную шахматную доску со стороной квадрата А наудачу бросается монета радиуса r меньше а/2. Найти вероятности следующих событий: А = «монета попадет целиком внутрь одного квадрата», В = «монета пересечет не более одной стороны квадрата».
Решение. 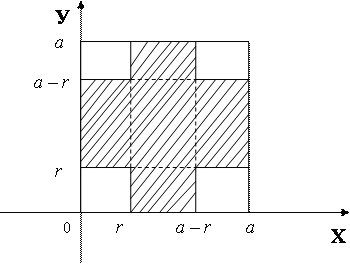
Пусть (Х, у) — координаты центра упавшей монеты (рис. 3.3). В силу бесконечности шахматной доски можно считать, что элементарные исходы данного эксперимента полностью определяются положением центра упавшей монеты относительно вершин квадрата, содержащего этот центр.
Помещая начало координат в одну из вершин указанного квадрата можно записать множество элементарных исходов в виде 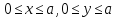 . Множество, соответствующее событию А: х
. Множество, соответствующее событию А: х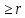 , y
, y , т. е. является квадратом со стороной a – 2r.
, т. е. является квадратом со стороной a – 2r.
Следовательно, S = (a-2r)2; S-a2; P(A)=(a-2r)2/a2 .
Ответ: (a-2r)2/a2 .
Список литературы и Интернет-ресурсов:
Новоселов О.В. Комбинаторика и вероятность: учебн. пособие для слушателей подготовит. курсов / О. В. Новоселов, Л.П. Скиба. СибГАУ, Красноярск, 2009. – 78 с.
Филимонова Л.В., Быкова Е.А. Математика и информатика. Учебное пособие (для студентов гуманитарных факультетов ВУЗов). – 2-е изд. Дополненное и переработанное – Елец, ЕГУ им. И.А. Бунина, 2001, 110 с.
https://ege-study.ru/ru/ege/materialy/matematika/teoriya-veroyatnostej-na-ege-po-matematike/
https://www.matburo.ru/tv_book.php





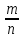 ,
,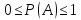
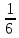 – из урны будет извлечён красный шар;
– из урны будет извлечён красный шар;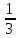 – из урны будет извлечён чёрный шар.
– из урны будет извлечён чёрный шар.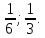
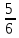
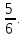
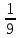 – искомая вероятность.
– искомая вероятность.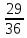 – вероятность того, что выпадет от трёх или до 9-ти очков.
– вероятность того, что выпадет от трёх или до 9-ти очков.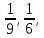
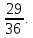
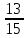
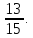
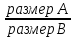 - геометрическое определение вероятности.
- геометрическое определение вероятности.

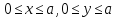 . Множество, соответствующее событию А: х
. Множество, соответствующее событию А: х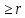 , y
, y
















