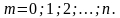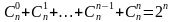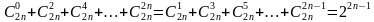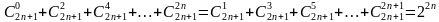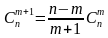Лекция «Комбинаторика»
План:
Комбинаторика и ее возникновение
Основные понятия комбинаторики и правила.
Перестановки, размещения, сочетания.
Треугольник Паскаля и бином Ньютона.
Применение комбинаторики.
Комбинаторика и ее возникновение
Элементарная комбинаторика имеет дело с множествами, из которых выбираются подмножества с определенными свойствами. Как правило, основной вопрос заключается в следующем: сколько таких подмножеств можно выбрать из данного множества? То есть задача состоит в подсчете числа этих подмножеств. Кроме того, в комбинаторике изучаются и разрабатываются методы подсчета числа подмножеств с заданными свойствами.
Комбинаторика возникла в XVI веке. В жизни привилегированных слоев тогдашнего общества большое место занимали азартные игры (карты, кости). Широко были распространены лотереи. Первоначально комбинаторные задачи касались в основном азартных игр: сколькими способами можно получить данное число очков, бросая 2 или 3 кости или сколькими способами можно получить 2-ух королей в некоторой карточной игре. Эти и другие проблемы азартных игр являлись движущей силой в развитии комбинаторики и далее в развитии теории вероятностей.
Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицы (числа способов выпадения k очков на r костях). Однако он не учел, одна и та же сумма очков может выпасть различными способами, поэтому его таблицы содержали большое количество ошибок.
Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские математики Блез Паскаль и Ферма. Исходным пунктом их исследований были так же проблемы азартных игр.
Дальнейшее развитие комбинаторики связано с именами Я. Бернулли, Г. Лейбница, Л. Эйлера. Однако и в их работах основную роль играли приложения к различным играм.
Сегодня комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний, для составления планов производства и реализации продукции и прочее.
Основные понятия и правила комбинаторики
Введем следующие понятия. Пусть A = {a1, . . . , an} – множество из n элементов. Комбинаторный объект – это подмножество с определенными свойствами из элементов множества A. Комбинаторное число (связанное с комбинаторным объектом) – это количество комбинаторных объектов этого вида.
Часто при подсчете числа комбинаторных объектов применяются два основных приема: правило суммы и правило произведения.
Правило суммы: Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить m + n способами.
Пример: В меню столовой колледжа 2 вида холодных закусок, 5 вариантов первых блюд и 7 вариантов вторых. Сколькими способами можно выбрать ОДНО БЛЮДО?
Решение: В задаче рассматриваются три группы: холодные закуски, первые и вторые блюда. Сколько элементов в группах? Закуску можно выбрать 2 способами; первое блюдо выбрать 5 способами; второе блюдо можно выбрать 7 способами. Видим, что в группах нет одинаковых элементов. Применим закон сложения: 2+5+7=14.
Ответ: блюдо можно выбрать 14 способами.
Правило произведения: Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить m ∙ п способами.
Пример: На витрине кафе представлено 15 вариантов десертов. Ребята из них выбирают 3 десерта. Выясните, сколькими различными способами можно выбрать 3 десерта?
Решение: Сначала ребята могут выбрать любой из всех 25 десертов. Когда первый выбор сделан, для следующего остаётся 15−1=14 вариантов выбора десерта. 1-й десерт выбирают 15 способами, 2 -й десерт выбираем 14 способами. Используем правило произведения: 2 десерта выбираем 15⋅14=210 (способами).
Ответ: Ребята могут выбрать десерт 210 различными способами.
Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n.
Обозначение: n!
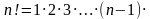
Факториа́л числа n! (лат. factorialis — действующий, производящий, умножающий. Факториал это своеобразная единица измерения комбинаторики. Например: 5!=5*4*3*2*1=120
4!=4*3*2*1=24, то есть 5!=5*4!
Важно! 0!=1
Перестановки, размещения, сочетания
Перестановкой называется конечное множество, в котором установлен порядок элементов. Число всевозможных перестановок из n элементов вычисляется по формуле: Pn = n!
Важно! В заданиях на перестановки, не важно назвать сами перестановки, а важно назвать их число.
Пример: В колледже для концерта подготовили 5 танцевальных композиций. В концертной программе один раз нужно представить каждую композицию. Сколько можно составить концертных программ, если порядок важен?
Решение: Так как количество элементов во множестве неизменно и порядок элементов важен, можно сделать вывод, что нужно вычислить число перестановок: Pn=n!, P5=5!=5⋅4⋅3⋅2⋅1=120
Ответ: можно составить 120 различных концертных программ.
Перестановки с повторениями - Число перестановок n – элементов, в котором элементов i –того типа ( 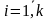 ) вычисляется по формуле:
) вычисляется по формуле:
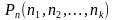 =
= 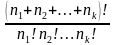
Пример 1: Сколько слов можно составить, переставив буквы в слове «математика»?
Решение: «математика» - 10 букв ( с повт. м=2,а=3,т=2,е=и=к=1),
Ответ: 151200 слов.
Пример 2: Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, и 4, причём в каждом числе цифры должны быть разные?
Решение: Р5 – Р4 = 5! – 4! = 120 – 24 = 96.
Ответ: 96 чисел.
Размещения. Комбинации, в которых имеет значение порядок элементов, называются размещениями.
В размещениях у каждого элемента своя определённая роль. Размещения — это упорядоченные наборы.
Например: пара учеников — староста класса и его помощник; пара цифр — десятки и единицы.
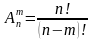 , где n-показывает количество элементов данного множества, m показывает количество элементов размещения (сколько элементов выбирается).
, где n-показывает количество элементов данного множества, m показывает количество элементов размещения (сколько элементов выбирается).
Пример: Для прохождения практики студентов есть14 автомобильных сервисов. Сколькими способами можно устроить трёх человек, чтобы они были в разных сервисах?
Решение: Требуемая выборка — размещение, т.к. порядок элементов важен. Например, если первый человек будет работать в сервисе A, второй — в B, а третий — в C. Меняя местами людей, получатся новые ситуации — новые выборки. Нужно вычислить, сколькими способами можно выбрать m элементов из n элементов, где n=14; m=3 Применяя формулу, получаем
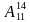 =
= 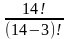 =
= 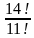 =
= 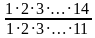 = 2184.
= 2184.
Ответ: 2184 способ.
Размещения с повторениями. k – размещением с повторениями n–элементного множества называется упорядоченный набор длины k элементов данного множества. Число k – размещений с повторениями вычисляется по формуле:
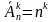
Пример: A=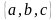 , 2- размещения с повторениями/
, 2- размещения с повторениями/
Решение: (a;b), (b;a), (a;c), (c;a), (b;c), (c;b), (a;a), (b;b), (c;c) или 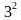 = 9.
= 9.
Ответ: 9 размещений.
Сочетания. Подмножества, составленные из n элементов данного множества и содержащие k элементов в каждом подмножестве, называют сочетаниями из n элементов по k. (Сочетания различаются только элементами, порядок их не важен: ab и ba – это одно и тоже сочетание).
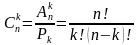 .
.
Пример: Сколькими способами можно выбрать трёх дежурных из класса, в котором 20 человек?
Решение: 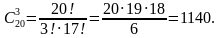
Ответ: 1140 способами.
Треугольник Паскаля и бином Ньютона

Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид где — биномиальные коэффициенты, — неотрицательное целое число.
«Би»-удвоение, раздвоение … «Ном»(фран. nombre) –номер, нумерация. «Бином» -»два числа»
Бином Ньютона – это выражение вида 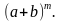
Треугольником Паскаля пользуются при возведении бинома (a+b) в натуральные степени.
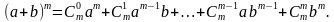
Свойства коэффициентов бинома Ньютона:
Свойство 1. 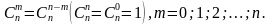
Свойство 2. 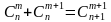 ,
, 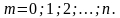
Свойство 3. 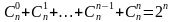
Свойство 4. 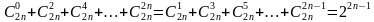
Свойство 5. 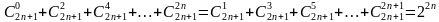
Свойство 6. 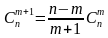
Применение комбинаторики
Комбинаторика как раздел математики имеет широкий спектр применения в различных областях знаний. Статья посвящена рассмотрению комбинаторных объектов в жизнедеятельности человека и решению комбинаторных задач на составление автомобильных номеров. Исследование показало, что для развития современной системы математического образования комбинаторика обладает высоким творческим потенциалом.
Комбинаторика связана со многими другими областями математики – алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например, в генетике, информатике, статистической физике).
Кроме этого можно выделить следующее:
- учебные заведения (составление расписаний);
- сфера общественного питания (составление меню);
- лингвистика (рассмотрение вариантов комбинаций букв);
- биология (расшифровка кода ДНК);
- экономика (анализ вариантов купли-продажи акций);
- география (раскраска карт);
- спортивные соревнования (расчёт количества игр между участниками);
- производство (распределение нескольких видов работ между рабочими);
- астрология (анализ расположения планет и созвездий);
- криптография (разработка методов шифрования);
- агротехника (размещение посевов на нескольких полях);
- азартные игры (подсчёт частоты выигрышей);
- химия (анализ возможных связей между химическими элементами);
- военное дело (расположение подразделений);
- доставка почты (рассмотрение вариантов пересылки) и прочее.







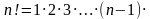
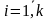 ) вычисляется по формуле:
) вычисляется по формуле: 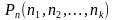 =
= 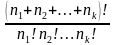
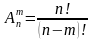 , где n-показывает количество элементов данного множества, m показывает количество элементов размещения (сколько элементов выбирается).
, где n-показывает количество элементов данного множества, m показывает количество элементов размещения (сколько элементов выбирается).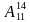 =
= 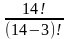 =
= 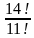 =
= 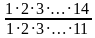 = 2184.
= 2184. 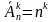
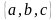 , 2- размещения с повторениями/
, 2- размещения с повторениями/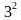 = 9.
= 9.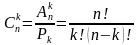 .
.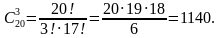

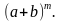
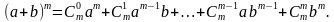
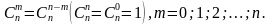
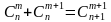 ,
,