
Электронный курс лекций
«Математический анализ»
Лекция 2. Сходящиеся последовательности. Монотонные последовательности. Основные теоремы. Свойства сходящихся последовательностей .
к.п.н., преподаватель высшей категории Никитин М.Е. Раменское, 2015
Лекция 2. Сходящиеся последовательности. Монотонные последовательности. Основные теоремы.
Свойства сходящихся последовательностей
Теорема 1
Сходящаяся последовательность имеет только один предел.
Доказательство
Пусть a и b – пределы сходящейся последовательности . Используя формулу (2) можно записать и , где , - бесконечно малые последовательности. Вычитая, получим Так как, все элементы последовательности имеют одно и тоже значение b - a , то по теореме 5 (см. ранее) b - a =0 и b = a . Теорема доказана.
Теорема 2
Сходящаяся последовательность ограничена.
Доказательство
Пусть последовательность сходящаяся и а – ее предел. Имеет место формула
, - бесконечно малая последовательность. Так как бесконечно малая последовательность - ограничена (теорема 3), то справедливо
. Поэтому для всех номеров n , что и означает ограниченность последовательности .
Замечание
Ограниченная последовательность может быть и не сходящейся.
Например
1,-1,1,-1,… - ограничена, но не сходящаяся. Если бы последовательность сходилась, то
и - бесконечно малые последовательности и
была бы бесконечно малой последовательностью, но
,

Теорема 3
Сумма сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей и
.
Доказательство
Пусть и . Тогда и , соответственно . Таким образом, последовательность
- бесконечно малая, и поэтому последовательность сходится и имеет своим пределом a + b .
Теорема 4
Разность сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен разности пределов последовательностей
и . Доказательство аналогичное.
Теорема 5
Произведение сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей и .
Доказательство
и
Пусть
, соответственно
и
. Тогда
. Но в силу теоремы 4 (для бесконечно
малых последовательностей, следствия из него и теоремы 1)
сходится и ее предел - ab .
- бесконечно малая последовательность. То есть
Лемма
Если последовательность
сходится, то есть
, то, начиная с

некоторого номера, определена последовательность , которая является ограниченной.
Доказательство
Пусть . Так как . Пусть N – номер, соответствующий этому ,
начиная с которого выполняется неравенство . Из этого
неравенства следует, что при выполняется неравенство . Действительно
Поэтому, при имеем . Следовательно, начиная с этого номера N ,
можно рассматривать последовательность , и эта последовательность ограничена. Лемма доказана.
Теорема 6
Частное двух сходящихся последовательностей и при условии, что предел последовательности отличен от 0, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей и .
Доказательство
Из леммы следует, что, начиная с некоторого номера N элементы не равны 0 и
последовательность - ограничена. Начиная с этого номера, рассмотрим
последовательность .
.
Пусть
и

Докажем, что
- бесконечно малая последовательность. Так как
и
, то
Так как - ограничена, а последовательность - бесконечно малая, то
последовательность - бесконечно малая, то есть
. Теорема доказана.
Предельный переход в неравенствах
Неравенства, которым удовлетворяют элементы сходящихся последовательностей, в пределе переходят в соответствующие неравенства для пределов этих последовательностей.
Имеют место теоремы.
Теорема 1
Если элементы сходящейся последовательности , начиная с некоторого номера, удовлетворяют неравенству , то и предел а этой последовательности
удовлетворяет неравенству
![Доказательство и , начиная с некоторого номера удовлетворяют неравенству Покажем, что . Предположим обратное, то есть a b . Так как , тогда положим и для можно указать , что при выполняется . То есть или . Используя правое неравенство, получим , а это противоречит условию теоремы. Следствие 1 Если элементы сходящихся последовательностей и , начиная с некоторого номера, удовлетворяют неравенству , то . Следствие 2 Если элементы сходящейся последовательности находятся на сегменте [ a , b ], то и Теорема 2 Пусть и . Пусть также начиная с некоторого номера элементы последовательности удовлетворяют неравенству , тогда Монотонные последовательности Определение Последовательность называется неубывающей (невозрастающей), если для всех номеров n справедливо неравенство Общее название – монотонные последовательности. Если для всех n - возрастающая. Если для всех n - убывающая. Общее название – строго монотонные. Монотонные последовательности ограничены либо сверху, либо снизу.](https://fsd.multiurok.ru/html/2022/04/16/s_625a951066134/img5.jpg)
Доказательство
и , начиная с некоторого номера удовлетворяют неравенству Покажем, что . Предположим обратное, то есть a b . Так как , тогда положим и для можно указать , что при выполняется . То есть или . Используя правое неравенство, получим , а это противоречит условию теоремы.
Следствие 1
Если элементы сходящихся последовательностей и , начиная с некоторого номера, удовлетворяют неравенству , то .
Следствие 2
Если элементы сходящейся последовательности находятся на сегменте [ a , b ], то и
Теорема 2
Пусть и . Пусть также начиная с некоторого номера элементы последовательности удовлетворяют неравенству , тогда
Монотонные последовательности
Определение
Последовательность называется неубывающей (невозрастающей), если для всех номеров n справедливо неравенство
Общее название – монотонные последовательности.
Если для всех n - возрастающая.
Если для всех n - убывающая.
Общее название – строго монотонные.
Монотонные последовательности ограничены либо сверху, либо снизу.

Невозрастающие – ограничены сверху;
Неубывающие – ограничены снизу;
Невозрастающая последовательность ограничена с двух сторон, если она ограничена снизу.
Неубывающая последовательность ограничена с двух сторон, если она ограничена сверху
Примеры.
1. невозрастающая, ограничена сверху 1, снизу – 0.
2. неубывающая, ограничена снизу - 1.
3. возрастающая, ограничена снизу , сверху – 1.
Признак сходимости монотонной последовательности.
Теорема
Если неубывающая (невозрастающая) последовательность ограничена сверху (снизу), то она сходится (основная теорема).
Другая формулировка
Если монотонная последовательность ограничена с обеих сторон, то она сходится.
- ограничена, то
Доказательство
Последовательность
и
- точные верхняя и нижняя грани.
Докажем, что если последовательность неубывающая, то - ее предел;
Если последовательность невозрастающая, то - ее предел;
Ограничимся случаем неубывающей последовательности.
Поскольку - верхняя грань множества элементов последовательности, то
, такой, что и . Сопоставляя неравенства, получаем . Так как - неубывающая последовательность, то при
справедливо неравенство . Выше было
неравенство , тогда или . Таким образом, - предел .
Замечание 1
Условие ограниченности монотонной последовательности представляет собой необходимое и достаточное условие ее сходимости.
Замечание 2
Сходящаяся последовательность может и не быть монотонной. Например - сходящаяся, так как . Но она не монотонная.
Свойства числовых последовательностей и числовых множеств
Подпоследовательности числовых последовательностей
Пусть - некоторая числовая последовательность. Рассмотрим последовательность . Выбираем из элементы с
номерами , то есть - это подпоследовательность
последовательности .
Свойство 1
Если для , то любая подпоследовательность этой
последовательности имеет своим пределом число а.

Справедливо и обратное.
Если все подпоследовательности последовательности сходятся, то пределы этих подпоследовательностей равны одному и тому же числу а; в частности, к этому же числу сходится и последовательность .
Свойство 2
Каждая подпоследовательность бесконечно большой последовательности также будет бесконечно большой.
Свойство 3
Из каждой сходящейся последовательности можно выделить монотонную сходящуюся подпоследовательность.
Предельные точки последовательности
Определение 1
Точка х бесконечной прямой называется предельной точкой последовательности , если любой - окрестности этой точки имеется бесконечно много элементов последовательности .
Лемма 1
Если х – предельная точка последовательности , то из этой последовательности можно выделить подпоследовательность , сходящуюся к числу х .
Доказательство
Пусть х – предельная точка . Рассмотрим систему - окрестностей точки х :
Выберем и так далее.
Это процесс можно продолжить бесконечно, так как в - окрестности точки х имеется бесконечно много элементов последовательности .
В результате получаем подпоследовательность , которая сходится к х , так как
. Теорема доказана.
Замечание
Справедливо обратное утверждение: Если из последовательности можно выделить подпоследовательность , сходящуюся к числу х , то х является предельной точкой и для .
Определение 2
Точка х называется предельной точкой последовательности , если из этой последовательности можно выделить подпоследовательность , сходящуюся к х .
Лемма 2
Каждая сходящаяся последовательность имеет только одну предельную точку, совпадающую с пределом этой последовательности.
Доказательство
Отметим, что предел а сходящейся последовательности является предельной точкой этой последовательности, поскольку в - окрестности точки а содержатся все элементы последовательности, начиная с некоторого номера. Убедимся, что у нет других предельных точек. Действительно, пусть b - предельная точка сходящейся последовательности. В силу леммы 1 из можно выделить подпоследовательность
, сходящуюся к b . Но любая подпоследовательность сходящейся последовательности имеет предел а (на основании определения предельной точки) и поэтому b = a .
Существование предельной точки у ограниченной последовательности

Теорема
У всякой ограниченной последовательности существует хотя бы одна предельная точка.
Определение 1
Наибольшая предельная точка последовательности называется верхним пределом этой последовательности.
Обозначение последовательности
У всякой ограниченной последовательности существует верхний предел.
Определение 2
Наименьшая предельная точка последовательности называется нижним пределом этой последовательности.
Обозначение последовательности
У всякой ограниченной последовательности существует нижний предел.
Окончательно
У всякой ограниченной последовательности существует верхний и нижний пределы.
Следствие 1
Если ( a , b ) – интервал, вне которого лежит лишь конечное число элементов ограниченной последовательности , а и - верхний и нижний пределы этой последовательности, то интервал ) содержится в интервале ( a , b ) и поэтому
.
Следствие 2
Для интервал ) содержит все элементы последовательности , начиная с некоторого номера.
Замечание
Ограниченная последовательность в общем случае может иметь любое количество
предельных точек (конечное или бесконечное). Пусть и - верхний и нижний пределы этой последовательности. Очевидно, что все предельные точки последовательности лежат на сегменте (сколько бы их не было).
Если - то последовательность имеет только одну предельную точку.
Если - то последовательность имеет две предельные точки.
Пример
имеет две предельные точки .
О выделении сходящейся последовательности. Теорема Больцано-Вейерштрасса.
Теорема
Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Доказательство
Так как последовательность ограничена, то она имеет хотя бы одну предельную точку х . В таком случае из этой последовательности можно выделить подпоследовательность, сходящуюся к точке х (см. определение 2 предельной точки).
Замечание 1
Из любой ограниченной последовательности можно выделить монотонную подпоследовательность.
В силу теоремы Больцано-Вейерштрасса из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность, а из этой подпоследовательности можно выделить монотонную подпоследовательность.
Замечание 2
Пусть ограниченная последовательность, элементы которой находятся на сегменте [ a , b ] . Тогда предел с любой сходящейся подпоследовательности также находится на сегменте [ a , b ].

Действительно, так как
Замечание 3
В отдельных случаях из неограниченной последовательности можно выделить сходящуюся подпоследовательность.
Например
неограниченно, но подпоследовательность
сходится.
Необходимое и достаточное условие сходимости последовательности
Существует внутренний критерий сходимости последовательности исходя из величины элементов. Для формулировки этого критерия введем понятие фундаментальной последовательности.
Определение
Последовательность называется фундаментальной, если , такой, что для всех номеров n , удовлетворяющих условию и для всех натуральных чисел p (p=1,2,…) справедливо неравенство
Теорема 1
Для того, чтобы последовательность была сходящейся, необходимо и достаточно, чтобы она была ограниченной и чтобы нижний и верхний пределы ее совпадали, то есть
Теорема 2 (важное свойство фундаментальной последовательности)
Для фундаментальной последовательности, - окрестности которого находятся все элементы последовательности, начиная с номера N .
Другими словами, вне интервала находится не более чем конечное число элементов последовательности.
Отмеченное свойство позволяет установить ограниченность фундаментальной последовательности.
Пусть и - элемент, в - окрестности которого находятся все элементы, начиная с номера N . Тогда вне этой - окрестности могут находиться только элементы . Положим . Тогда на сегменте [- A , A ] находятся числа , а следовательно, и все точки - окрестности числа . Отсюда вытекает, что все элементы фундаментальной последовательности находятся на сегменте [- A , A ] , что и означает ее ограниченность.
Теорема. Критерий Коши сходимости последовательности.
Для того, чтобы последовательность была сходящейся необходимо и достаточно, чтобы она была фундаментальной.
Доказательство
Необходимость
Пусть - сходящаяся, и х – ее предел. Требуется доказать, что эта последовательность фундаментальная.
Возьмем . Из определения сходимости последовательности вытекает, что для
, такой, что при выполняется неравенство . Если
, то при выполняется также и неравенство .
Из последних неравенств получаем
Фундаментальность установлена.

Достаточность
Пусть - фундаментальная последовательность. Требуется доказать, что эта последовательность сходится. Для этого достаточно доказать ограниченность и равенство ее верхнего и нижнего пределов и . Ограниченность фундаментальной последовательности уже была установлена выше. Для доказательства равенства пределов воспользуемся рассмотренным ранее свойством фундаментальной последовательности: Для фундаментальной последовательности, в - окрестности которого находятся все элементы последовательности, начиная с номера N .
Другими словами, вне интервала находится не более чем конечное число элементов последовательности.
На основании теоремы: ( у всякой ограниченной последовательности существует хотя бы одна предельная точка и следствия из данной теоремы) интервал содержит интервал , и поэтому , откуда в силу произвольности
. Тем самым сходимость установлена и теорема доказана.







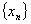 , если для любого положительного числа E существует такой номер N, что при всех N>N выполняется неравенство
, если для любого положительного числа E существует такой номер N, что при всех N>N выполняется неравенство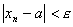
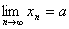 , или
, или 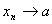 При
При 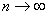 .
.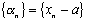 есть бесконечно малая, так как для любого
есть бесконечно малая, так как для любого 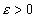 существует такой номер N, что при
существует такой номер N, что при 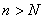 выполняется неравенство
выполняется неравенство 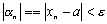 . Следовательно, любой элемент
. Следовательно, любой элемент 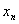 сходящейся последовательности, имеющей предел а, можно представить в виде:
сходящейся последовательности, имеющей предел а, можно представить в виде: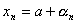 ,
,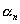 – элемент бесконечно малой последовательности
– элемент бесконечно малой последовательности  .
.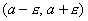 называют E–окрестностью точки А.
называют E–окрестностью точки А.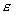 –окрестности остается конечное число элементов. Поэтому предел последовательности часто называют точкой сгущения.
–окрестности остается конечное число элементов. Поэтому предел последовательности часто называют точкой сгущения.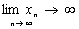
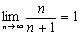 .
. . Так как
. Так как 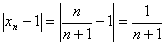 , то для удовлетворения неравенству (9.1.1) достаточно решить неравенство
, то для удовлетворения неравенству (9.1.1) достаточно решить неравенство 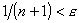 , откуда получаем
, откуда получаем 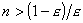 , неравенство
, неравенство 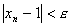 будет выполняться при всех N>N, где
будет выполняться при всех N>N, где 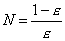 .
.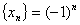 или –1, 1, –1, 1, … не имеет предела. Действительно, какое Бы число мы ни предложили в качестве предела, 1 или –1, при
или –1, 1, –1, 1, … не имеет предела. Действительно, какое Бы число мы ни предложили в качестве предела, 1 или –1, при 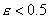 неравенство (4.2.2), определяющее предел последовательности, не удовлетворяется: вне
неравенство (4.2.2), определяющее предел последовательности, не удовлетворяется: вне 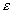 – окрестности этих чисел остается бесконечное число элементов
– окрестности этих чисел остается бесконечное число элементов 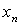 : все элементы с нечетными номерами равны –1, элементы с четными номерами равны 1.
: все элементы с нечетными номерами равны –1, элементы с четными номерами равны 1.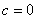 .
.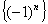 , рассмотренная в Примере 2, ограничена, но не имеет предела.
, рассмотренная в Примере 2, ограничена, но не имеет предела.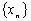 и
и 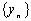 есть Сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей
есть Сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей 



![Доказательство и , начиная с некоторого номера удовлетворяют неравенству Покажем, что . Предположим обратное, то есть a b . Так как , тогда положим и для можно указать , что при выполняется . То есть или . Используя правое неравенство, получим , а это противоречит условию теоремы. Следствие 1 Если элементы сходящихся последовательностей и , начиная с некоторого номера, удовлетворяют неравенству , то . Следствие 2 Если элементы сходящейся последовательности находятся на сегменте [ a , b ], то и Теорема 2 Пусть и . Пусть также начиная с некоторого номера элементы последовательности удовлетворяют неравенству , тогда Монотонные последовательности Определение Последовательность называется неубывающей (невозрастающей), если для всех номеров n справедливо неравенство Общее название – монотонные последовательности. Если для всех n - возрастающая. Если для всех n - убывающая. Общее название – строго монотонные. Монотонные последовательности ограничены либо сверху, либо снизу.](https://fsd.multiurok.ru/html/2022/04/16/s_625a951066134/img5.jpg)
























