Квадратные уравнения и различные способы решения

МБОУ «Верхнемедведицкая СОШ»

Квадратные уравнения

Цель работы – систематизирование знаний по теме «Квадратные уравнения» .

Для достижения поставленной цели необходимо решить ряд задач :

• дать определение квадратным уравнениям;
• рассмотреть виды квадратных уравнений;
• изучить способы решения квадратных уравнений;
• ознакомиться с примерами решения квадратных уравнений.

Объектом исследования служат квадратные уравнения.

Предметом являются способы решения квадратных уравнений.

Гипотеза: любое квадратное уравнение можно решить существующими способами.

понятие квадратных уравнений

Квадратные уравнения – это уравнения вида

ax 2 + bx + c = 0 , где x - переменная,

a , b и c - некоторые числа, причём a ≠ 0 .

Число a – первый коэффициент,

число b – второй коэффициент,

число c – свободный член.

Решить квадратное уравнение - значит найти все его корни или установить, что корней нет

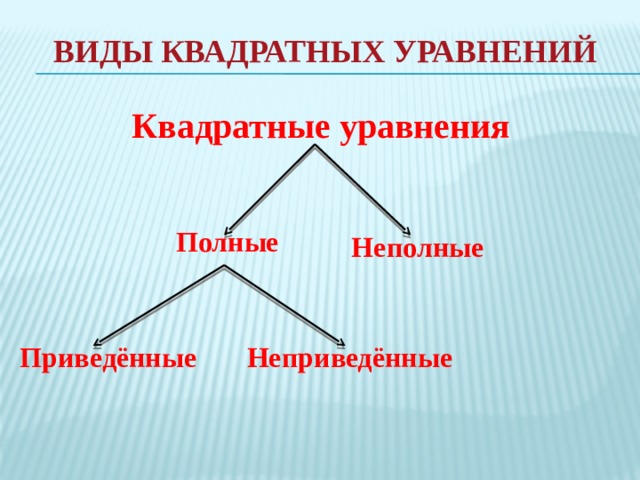
Виды квадратных уравнений

Квадратные уравнения

Полные

Неполные

Неприведённые

Приведённые

Полные квадратные уравнения

Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых, у которого коэффициенты a , b и c отличны от нуля

ax 2 + bx + c = 0

6x 2 + 3 x + 1 = 0

a=6 b=3 c=1

Приведенное квадратное уравнение – это квадратное уравнение, в котором коэффициент a = 1

x 2 + bx + c = 0

x 2 + 3 x + 5 = 0

a=1 b=3 c=5

Неприведенное квадратное уравнение – это квадратное уравнение, в котором коэффициент a ≠ 1

ax 2 + bx + c = 0

3x 2 + 4 x + 2 = 0

a=3 b=4 c=2

0 , то Если D = 0 , то уравнение имеет уравнение имеет уравнение не 2 корня 1 корень имеет корней " width="640"

Решение полных квадратных уравнений

ax 2 + bx + c = 0

1. Определить коэффициенты a , b и c

2. Вычислить дискриминант

D=b 2 – 4ac

Если D

Если D 0 , то

Если D = 0 , то

уравнение имеет

уравнение имеет

уравнение не

2 корня

1 корень

имеет корней

0, корней 2 D 2) 16 x 2 - 8 x + 1 = 0 a = 16 b = -8 c = 1 D = b 2 – 4 ac D = (-8) 2 – 4 · 16 · 1 = 64 – 64 = 0 D = 0, корень 1 " width="640"

Примеры решения полных квадратных уравнений

1) 2 x 2 + x + 5 = 0

3) x 2 - 11x + 30 = 0

a = 2 b = 1 c = 5

a = 1 b = -11 c = 30

D = b 2 – 4 ac

D = b 2 – 4ac

D = 1 2 – 4 · 2 · 5 = 1 – 40 = -39

D = (-11) 2 – 4 · 1 · 30 = 121 – 120 = 1

D 0, корней 2

D

2) 16 x 2 - 8 x + 1 = 0

a = 16 b = -8 c = 1

D = b 2 – 4 ac

D = (-8) 2 – 4 · 16 · 1 = 64 – 64 = 0

D = 0, корень 1

неПолные квадратные уравнения

Неполные квадратные уравнения – это квадратные уравнения, в которых хотя бы один из коэффициентов b или c равен нуля

ax 2 + bx = 0

a ≠ 0, b ≠ 0, с = 0

ax 2 + c = 0

a ≠ 0, b = 0, с ≠ 0

ax 2 = 0

a ≠ 0, b = 0, с = 0

Решение неполных квадратных уравнений

с = 0

b = 0

b = 0, с = 0

ax 2 + bx = 0

ax 2 + c = 0

ax 2 = 0

1. Вынести общий множитель x за скобки

x (ax + b) = 0

2. Разбить уравнение на два равносильных

x = 0 и ax + b = 0

3. Два решения ( один из корней всегда 0 ):

x = 0 и ax + b = 0

ax = - b

1. Перенести с в правую часть уравнения

ax 2 + c = 0

2. Разделить обе части уравнения на а

3. Если

Если

1. Разделить обе части

уравнения на a

x 2 = 0

2. Одно решение

x = 0

Примеры Решения неполных квадратных уравнений

b = 0, с = 0

b = 0

с = 0

1) 6 x 2 + 18 x = 0

1) 3x 2 - 12 = 0

x 2 = 12:3

x · ( 6 x + 18) = 0

x 2 = 4

x = 0 и 6 x + 18 = 0

6 x + 18 = 0

x = -18 : 6

x = - 3

x 1 = 0

x 2 = - 3

2) 2 x 2 - 12 x = 0

x · (2x - 12) = 0

x = 0 и 2 x - 12 = 0

2 x - 12 = 0

x = 12 : 2

x = 6

x 1 = 0

x 2 = 6

1) 6 x 2 = 0

x 2 = 0 : 6

x 2 = 0

x = 0

2) 15 x 2 = 0

x 2 = 0 : 15

x 2 = 0

x = 0

2) 4 x 2 + 36 = 0

x 2 = - 36:4

x 2 = - 9

Корней нет

Решение квадратных уравнений по теореме виета

Теорема Виета

Сумма корней приведённого квадратного уравнения x 2 + px + q = 0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Итак,

По теореме Виета решаются только приведённые квадратные уравнения (коэффициент a = 1 ).

Если квадратное уравнение не является приведенным, но задание связано с применением теоремы, нужно обе части разделить на коэффициент, который располагается перед x 2 .

Примеры Решения квадратных уравнений по теореме виета

1)

Имея эти два равенства можно подобрать подходящие корни, которые будут удовлетворять как равенству обоим равенствам системы.

Подбор корней удобнее выполнять с помощью их произведения. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству .

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. Значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 являются корнями уравнения x 2  − 6x + 8 = 0

2)

Метод подбора находим корни:

Решение квадратных уравнений методом «переброски»

Метод «переброски» - решение неприведённых и непреобразуемых к виду приведённых с целыми коэффициентами путём их деления на старший коэффициент уравнений к решению приведённых с целыми коэффициентами.

1) умножим (буквально перебросим) все части на   а :

2) вводим новую переменную y = ax :

3) решим уравнение с помощью теоремы Виета:

4) вернемся к переменной x . Для этого разделим полученные результаты y 1,2  на первый коэффициент исходного уравнения, т.е. на a . Получим:

Примеры Решение квадратных уравнений методом «переброски»

2) 3 x 2 + 10 x + 7 = 0

1) 2 x 2 - 11 x + 15 = 0

умножим все части на 3 :

умножим все части на 2 :

2·2 x 2 - 2·11 x + 2·15 = 0

3·3 x 2 + 3·10 x + 21 = 0

вводим новую переменную y = 3x

вводим новую переменную y = 2x

y 2 - 11y + 30 = 0

y 2 + 10y + 21 = 0

решим с помощью теоремы Виета:

решим с помощью теоремы Виета:

вернемся к переменной x . Для этого разделим полученные результаты y 1,2  на первый коэффициент исходного уравнения, т.е. на 2 . Получим:

вернемся к переменной x . Для этого разделим полученные результаты y 1,2  на первый коэффициент исходного уравнения, т.е. на 3 . Получим:

вывод

Таким образом, существуют различные способы, которые позволяют очень быстро и рационально решать любое квадратное уравнение.

источники

https://studbooks.net/2402392/matematika_himiya_fizika/sposoby_resheniya_kvadratnyh_uravneniy

https://multiurok.ru/index.php/files/15-sposobov-rieshieniia-kvadratnykh-uravnienii.html

https://math-prosto.ru/?page=pages/theorem_of_vieta/how_to_solve_equations_with_vieta.php

http://spacemath.xyz/teorema-vieta/

https://skysmart.ru/articles/mathematic/teorema-vieta-formula

https://moluch.ru/archive/111/27959/

https://blog.tutoronline.ru/reshenie-kvadratnyh-uravnenij-metodom-perebroski

СПАСИБО ЗА ВНИМАНИЕ!