Теоретический материал по теме
«Случайная величина. Понятия непрерывной и дискретной случайных величин. Закон распределения случайной величины,
ее числовые характеристики»
Случайная величина. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Например, число бракованных лампочек среди 10 купленных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2,….,10. Случайные величины обозначаются прописными буквами латинского алфавита: X, Y, Zи так далее, а их значения – соответствующими строчными буквами x, y, zи так далее.
Случайная величина называется дискретной, если множество её значений конечно или счетно, то есть множество её значений представляет собой конечную последовательность x1, x2,….xn или бесконечную последовательность x1, x2,..xn,…
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного множества. Число возможных значений непрерывной случайной величины бесконечно.
Законом распределения случайной величины называют соответствие между возможными значениями и их вероятностями. Его можно задавать таблично, аналитически и графически. Табличное задание закона:
| X | x1 | x2 | … | xi | … | xi |
| P | p1 | p2 | … | pi | … | pn |
,где x1,x2,…xn– возможности значения случайной величины Х;
p1,p2,…pn – вероятности случайной величины Х.
События X =x1, X =х2, ... X=хn - полная система попарно несовместимых событий, поэтому сумма их вероятностей равна 1.
р 1+ р2 +...+рп = 1.
Пример.
В издательстве выпущено 100 книг по овцеводству. Лотереей разыграны одна книга в 500 руб. и 10 по 10 руб. Найти закон распределения случайной величины х - возможного выигрыша одной книги.
Решение. Возможны значениях: Х1= 500, х2 = 10 ,х3 = 0. Вероятности: р1=0,01; р2 =0,1; р3=1 - (р1+ р2) = 0,89.
Закон распределения:
| X | 500 | 10 | 0 |
| P | 0,01 | 0,1 | 0,89 |
Функцией распределения случайной величины называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, то есть F(x) = P(Xx).
Кроме закона распределения, который дает полное представление о случайной величине, часто используют числа, которые описывают случайную величину суммарно. Такие числа называют числовыми характеристиками случайной величины. К ним относятся математическое ожидание, дисперсия и среднее квадратичное отклонение дискретной случайной величины.
Математическим ожиданием (М) дискретной величины называют сумму произведений всех ее возможных значений, умноженных на их вероятности.
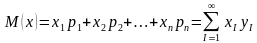 ,
,
где xi, - значение случайной величины, pi- вероятность случайной величины.
Часто требуется оценить рассеяние возможных значений случайной величины вокруг его среднего значения. Дисперсией (рассеянием) D(x) случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D(X) = М[Х-М(Х)]2.
Формула для вычисления дисперсии D(X) = М(Х2)-[М(Х)]2.
Свойства математического ожидания и дисперсии:
М(С) = С, c-const 1. D(C) = О, c-cоnst
М(СХ) = СМ(Х) 2. D(CX) = C2D(X), c-const
M(XV) = M(X) • M(V) 3. D(X+V) =D(X) + D(V)
4. M(X+M) = M(X) + M(V) 4. D(X-V) = D(X) + D(V)
Средним квадратичным отклонением (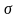 (х)) случайной величины хназывают квадратный корень из дисперсии:
(х)) случайной величины хназывают квадратный корень из дисперсии: 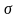 ( х )
( х ) 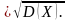
Исследование вариационных статистических рядов рассмотрим на примере.
Пример.: Дан дискретный вариационный ряд
где X {x1x2, x3} характеристики случайной величины X,N {n1, п2 ,п3} - частоты появления элементов в выборке.
Провести исследование дискретного вариационного ряда: 1) найти объём выборки, 2) составить закон распределения случайной величины X, 3) найти математическое ожидание, дисперсию и среднее квадратичное отклонение.
Решение. 1) Найдём объем выборки: п= n1+n2+п3=10+15+25=50.
2)Найдём относительные частоты: W1=10/50=1/5, w2=15/50=3/10, w3=25/50у =1/2.
Закон распределения случайной величины X представлен таблицей:
3) Найдём математическое ожидание, дисперсию и среднее квадратичное отклонение:
M=w1x1 + w2x2 + w3x3=l/5 • 1+3/10 ·4+1/2·6=4/4;
D= w1 (x1-M)2 + w2 (x2 -M)2+ w3 (x3 -M)2= 1/5 · (1-4,4) +3/10 · (4- 4,4) +1/2 · (6- 4,4)=3,64;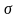 (x) =
(x) = 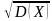 =
=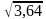 =1,9
=1,9
Задания для самостоятельного выполнения
Задание 1. Подготовка доклада на тему: «Функция распределения случайной величины».
Задание 2. Решение упражнений по темам раздела:
а) На пути движения автомашины 4 светофора, каждый из которых запрещает дальнейшее движение автомашины с вероятностью 0,5. Найти ряд распределения числа светофоров, пройденных машиной до первой остановки. Чему равны математическое ожидание и дисперсия этой случайной величины?
б) Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Составить закон распределения числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7. Найти дисперсию этой случайной величины.
в) Стрелок, имея 3 патрона, стреляет в цель до первого попадания. Вероятности попадания при первом, втором и третьем выстрелах соответственно 0,6, 0,5, 0,4. С.В. ξξ - число оставшихся патронов. Составить ряд распределения случайной величины, найти математическое ожидание, дисперсию, среднее квадратичное отклонение с.в., построить функцию распределения с.в., найти P(|ξ−m|≤σP(|ξ−m|≤σ.
г) В ящике содержится 7 стандартных и 3 бракованных детали. Вынимают детали последовательно до появления стандартной, не возвращая их обратно. ξξ - число извлеченных бракованных деталей. Составить закон распределения дискретной случайной величины ξξ, вычислить ее математическое ожидание, дисперсию, среднее квадратическое отклонение, начертить многоугольник распределения и график функции распределения.
д) На переэкзаменовку по теории вероятностей явились 3 студента. Вероятность того, что первый сдаст экзамен, равна 0,8, второй - 0,7, третий - 0,9. Найдите ряд распределения случайной величины ξξ числа студентов, сдавших экзамен, постройте график функции распределения, найдите М(ξ),D(ξ).
е) Вероятность попадания в цель при одном выстреле равна 0,8 и уменьшается с каждым выстрелом на 0,1. Составить закон распределения числа попаданий в цель, если сделано три выстрела. Найти математическое ожидание, дисперсию и С.К.О. этой случайной величины. Построить график функции распределения.
ж) По цели производится 4 выстрела. Вероятность попадания при этом растет так: 0,2, 0,4, 0,6, 0,7. Найти закон распределения случайной величины XX - числа попаданий. Найти вероятность того, что X≥1X≥1.







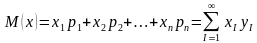 ,
,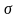 (х)) случайной величины хназывают квадратный корень из дисперсии:
(х)) случайной величины хназывают квадратный корень из дисперсии: 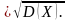
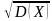 =
=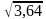 =1,9
=1,9

















