Математикада функция түшүнүгү эң бир негизги түшүнүктөрдүн бири экендиги анык. Мектеп курсунда элементардык деп аталчу бир нече функциялар б.а. алгебралык жана трансценденттик функциялар окутулуп келет. Атап айтканда: Сызыктуу, квадраттык, бөлчөктүү рационалдуу, көрсөткүчтүү, логарифмалык, иррационалдык, тригонометриялык, тескери тригонометриялык ж.б.у.с.
Мында окуучулар функциялардын монотондуулугун,
экстремумдарын, графиктин координата октору менен
кесилишкен чекиттерин аныктоону, графиктерди чийүүнү,
мезгилдүүлүгүн аныктоону ж.б. касиеттерин окуп келишкен.
Функциялар аркылуу турмуштагы көптөгөн процесстер
туюнтулат жана анын жардамында изилденет. Ар бир функция
өзүнчө касиеттерге ээ болгондуктан, аларды терең окуп
үйрөнүү ар бир окуучуга милдеттендирилет. Атап айтсак
функциялардын монотондуулугун, экстремумдарын,
графиктерин, мезгилдүүлүгүн ж.б. өздөштүрө билүүсү
окуучунун математиканы жакшы өздөштүрө алышына алып
келет.
Бул колдонмо бүгүнкү күндөгү окуучуларга жана
студентерге функцияларды окуп үйрөнүүдөгү кезигип жаткан
айрым проблемаларын чечүүгө жардам берет деген ойдобуз.
Ал проблемалардын чыгышынын бирден-бир себеби болуп
функциялар жөнүндө окуу куралдарынын, методикалык
колдонмолордун жетишсиздиги, ошондой эле окуучулардын
функцияларды окуп үйрөнүүдө аларды бири-бири менен окшоштуруп, салыштырып окууну өздөштүрө албастыгында
деп билебиз.
Бул колдонмону жазуунун бирден-бир себеби болуп да
мына ошондой проблемаларды чечүүгө негизделген жана бул
колдонмо алар үчүн жардамчы окуу куралы болуп калат деген
гана ой.
Бир аргументтүү функциялар
Математикадагы функция жөнүндөгү түшүнүктү карап жатып, анын аныктоосун берүүдө, авторлор өз эмгектеринде өзүнүн көз карашы боюнча маалыматтарды берип келишерин билебиз. Ошол себептен функциянын аныктоолору ар бир автордун эмгектеринде түрдүүчө берилген жана алар мааниси боюнча бирдей.
Аныктама 1. Кандайдыр бир Х көптүгүнүн ар бир элементине башка бир У көптүгүнүн бирден ашпаган элементи кайсы бир эреженин же закондун негизинде туура келсе, анда мындай туура келүүчүлүк функция деп аталат жана y = f (x) түрүндө белгиленет (1-чийме).

Мындагы x көз каранды эмес өзгөрмө же аргумент, ал эми y болсо x тен көз каранды б.а. функция, ал эми f кандайдыр бир закон же эреже.
Аныктама 2. Аргументтин (көз каранды эмес өзгөрмөнүн)
кабыл алууга мүмкүн болгон бардык маанилеринин көптүгү функциянын аныкталуу областы деп аталат жана D( y)
аркылуу белгиленет.
Аныктама 3. Аргумент x тин ар бир маанисине берилген y
функциясы анык мааниге ээ боло тургандай маанилеринин
көптүгү функциянын өзгөрүү областы деп аталат жана E(y) аркылуу белгиленет.
Берилишинде x аргументинин үстүнөн алгебралык амалдар (кошуу, кемитүү, көбөйтүү, бөлүү, даражага көтөрүү, тамыр чыгаруу) жүргүзүлгөн функциялар алгебралык функциялар деп аталат.
Мисалы: y =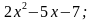 у=
у=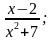 у=
у=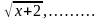
Төмөндө биз карай турган даражалуу, бүтүн, бөлчөктүү рационалдык жана иррационалдык функциялардын ар бири, алардын ар кандай комбинациялары алгебралык функциялар болушат.
Алгебралык эмес функциялардын бардыгы трансценденттик функциялар деп аталышат.
Трансценденттик функцияларга мисал болуп көрсөткүчтүү, логарифмалык, тригонометриялык жана тескери тригонометриялык функциялар эсептелет.
Мисалы: у= у=
у=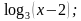 у=
у= у=
у=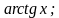
Эгерде x тин ар бир маанисине y тин бирден гана мааниси туура келсе, анда функция бир маанилүү деп, бир нече мааниси туура келсе, анда көп маанилүү деп аталат.
Эгерде x тин  маанисине y тин
маанисине y тин 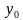 мааниси туура келсе, анда аны
мааниси туура келсе, анда аны 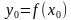 түрдө белгилешет.
түрдө белгилешет.
y = f (x) байланышын, функционалдык көз карандылык деп да коюшат. Функционалдык көз карандылыктар түрдүү жолдор менен берилет:
1. Аналитикалык жол.
2. Таблицалык жол.
3. Графиктик жол.
1).Функциянын аналитикалык жол менен берилет дегени, функционалдык көз карандылыктын жазылышы кандайдыр бир математикалык формулалар аркылуу берилендиги.
Мисалы: у=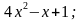 у=
у=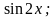 у=
у=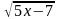 ж.б.у.с.
ж.б.у.с.
2) Функциянын таблицалык жол менен берилет дегени, функционалдык көз карандылыктын жазылышы, x тин ар бир кадамына б.а. тандалып алынган маанилерине y тин тиешелүү маанилери таблица аркылуу берилгени.
Мисалы: (Логарифманын, тригонометриянын ж.б. таблицалары)
3) Функциянын графиктик жол менен берилет дегени, мындагы функционалдык көз карандылыктын жазылышын, функциянын графиги аркылуу x тин ар бир маанисине туура келүүчү y тин тиешелүү маанилерин (мүмкүн жакындаштытырылган) табууга мүмкүн экендиги.
2. Функциянын түрлөрү жана касиеттери y = f (x) түрүндө берилген функцияны негизинен айкын түрдө берилген же бир өзгөрмөлүү функция деп коюшат.
1) Жуп жана так функциялар
Аныктама 1. Эгерде берилген y = f (x) функциясынын аныкталуу областынан алынган бардык x үчүн, f (- x) = f (x) барабардыгы аткарылса, анда y = f (x) жуп функция деп аталат.
Мисалы y = x2 , y = cos x ж.б.
Жуп функциялардын графиктери координаталык тегиздикте Оу огуна карата симметриялуу жайгашат (2-чийме).

Аныктама 2. Эгерде берилген y = f (x) функциясынын аныкталуу областынан алынган бардык x үчүн, f (- x) = - f (x) барабардыгы аткарылса, анда y = f (x) так функция деп аталат.
Мисалы y = 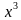 , y = sin x ж.б.
, y = sin x ж.б.
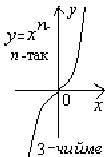
Так функциялардын графиктери координаталык тегиздикте
координата башталышына карата симметриялуу жайгашат
(3-чийме).
3. Функциянын монотондуулук аралыктары
Аныктама 1. Эгерде (а; b) аралыгынан алынган каалагандай  жана
жана 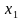 маанилеринде,
маанилеринде,  үчүн, f(
үчүн, f(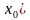 f(
f( барабарсыздыгы аткарылса, анда f (x) функциясы (а; b) аралыгында өсүүчү деп аталат (4-чийме). Кээде аргументтин чоң маанисине функциянын чоң мааниси (кичине мааниси) туура келсе, анда функция өсүүчү (кемүүчү) болот деп коюшат.
барабарсыздыгы аткарылса, анда f (x) функциясы (а; b) аралыгында өсүүчү деп аталат (4-чийме). Кээде аргументтин чоң маанисине функциянын чоң мааниси (кичине мааниси) туура келсе, анда функция өсүүчү (кемүүчү) болот деп коюшат.
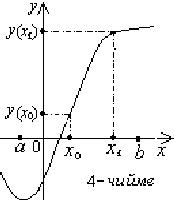
Мисалы у = 3х - 2 функциясы R аралыгында өсүүчү болот. Себеби х = 2 Î R 0 , х = 4 Î R 1 болгондо б.а.0 x x үчүн ( ) (2) 3 2 2 4 0 f x = f = × - = , ( ) (4) 3 4 2 10 1 f x = f = × - = , f (2) f (4)
болот, демек аргументтин чоң маанисине функциянын да чоң мааниси туура келип
Аныктама 2. Эгерде (а; b) аралыгынан алынган каалагандай
 жана
жана 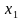 маанилеринде,
маанилеринде,  үчүн, f(
үчүн, f( барабарсыздыгы аткарылса, анда f (x) функциясы (а;b) аралыгында кемүүчү деп аталат (5-чийме).
барабарсыздыгы аткарылса, анда f (x) функциясы (а;b) аралыгында кемүүчү деп аталат (5-чийме).
Мисалы у = - х + 2 функциясы R аралыгында кемүүчү болот. Себеби  = 1
= 1 R ,
R , 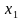 = 2
= 2  R болгондо б.а.
R болгондо б.а. 
үчүн f( , f(
f (1) f (2) болот, демек аргументтин чоң маанисине
функциянын кичине мааниси туура келип жатат.
Аныктама 3. Эгерде кандайдыр бир (a ; b) аралыкта берилген
y = f (x) функциянын туундусу  = f ' (x) 0 оң болсо, анда бул аралыкта функция өсүүчү, эгерде туунду y ' = f ' (x) 0 терс белгиде болсо, анда функция буk аралыкта кемүүчү функция болот.
= f ' (x) 0 оң болсо, анда бул аралыкта функция өсүүчү, эгерде туунду y ' = f ' (x) 0 терс белгиде болсо, анда функция буk аралыкта кемүүчү функция болот.
Мисалы. Туундунун жардамында f (x) = 2 - 5x + 3
- 5x + 3
функциясынын өсүү жана кемүү аралыктарын тапкыла.
Чыгарылышы. Функциянын аныкталуу областы бардык
чыныгы сандардын көптүгү болот. Демек, 
, 4x-5=0, x= мындан x
мындан x , болгондо, б.а функция (-
, болгондо, б.а функция (- аралыгында кемүүчү (
аралыгында кемүүчү ( аралыгында өсүүчү болот.
аралыгында өсүүчү болот.
Ал эми дайыма өсүүчү жана кемүүчү функцияларды монотондуу өсүүчү же кемүүчү функциялар деп аташат.
Аныктама 4. Эгерде  чекитинин (
чекитинин ( аймагынан алынган бардык
аймагынан алынган бардык  маанилери үчүн
маанилери үчүн
f (x) барабарсыздыгы орун алса, анда f (x) функциянын аныкталуу областынан алынган
барабарсыздыгы орун алса, анда f (x) функциянын аныкталуу областынан алынган  чекити функциянын минимум чекити деп аталат.
чекити функциянын минимум чекити деп аталат.
Мисалы.  = чекит, f (x) =
= чекит, f (x) =  - 4x + 4 функциясынын минимум чекити экендигин көрсөткүлө. Чыгарылышы.
- 4x + 4 функциясынын минимум чекити экендигин көрсөткүлө. Чыгарылышы.  = чекитинин аймагынан эркибизче 1,9 жана 2,1 маанилерин алалы. Функциянын бул чекиттердеги маанилерин эсептеп салыштырабыз:
= чекитинин аймагынан эркибизче 1,9 жана 2,1 маанилерин алалы. Функциянын бул чекиттердеги маанилерин эсептеп салыштырабыз:
f(1,9)= 1,9+4=3,61-7,6+4=0,01
1,9+4=3,61-7,6+4=0,01
f(2,1)=
f(2)
Демек,  = чекит чын эле f (x) =
= чекит чын эле f (x) =  - 4x + 4 функциясынын минимум чекити болот.
- 4x + 4 функциясынын минимум чекити болот.
Аныктама 5. Эгерде  чекитинин(
чекитинин( аймагынан алынган бардык
аймагынан алынган бардык  маанилери үчүн
маанилери үчүн
f(x) барабарсыздыгы орун алса, анда f (x) функциянын аныкталуу областынан алынган
барабарсыздыгы орун алса, анда f (x) функциянын аныкталуу областынан алынган  чекити функциянын максимум чекити деп аталат.
чекити функциянын максимум чекити деп аталат.
1.Ыктымалдуулуктар теориясынын алгачкы түшүнүктөрү.
Биз жашаган мейкиндиктен материалдык нерселерден башка дагы, ар кандай чексиз кѳп окуялар орун алышкан, жердин титиреши, суунун ташкындоосу, адамдардын эмгектениши жана мамилелеши, товарлардын ѳндγрγлγшγ жана сатылышы ж.у.с.
Ыктымалдыктар теорияси айлана-чѳйрѳ дγйнѳсγнγн обөективдγγ мыйзам ченемдγγлγктѳрγн изилдѳѳчγ математика илиминин бѳлγгγ болуп эсептелет. Айрыкча ал дγйнѳдѳгγ кокус окуялардын (кубулуштардын) массалык процесстерин изилдеп, окутуп-γйрѳтѳт. Макссалык кокус кубулуштары (окуялары) деп, талап коюлуучу шарттардыѳзгѳртпѳстѳн кѳп (каалаганча) ирээт кайталанган окуяларды айтабыз. Массалык процесстер кѳбγнчѳ ѳндγрγштѳ, социалдык жана экономикалык турмуштарда, ошондой эле согуш иштеринде ж.у.с. кездешет. Талап коюлуучу негизги шарттарды ѳзгѳртпѳсѳ деле тажрыйбанын жыйнтыктары бири-биринен айырмаланып калышы да мγмкγн, бирок бир тектγγ кѳптѳгѳн (массалык) окуялар γчγн тийиштγγ болгон мыйзам ченемдγγлγктѳрдγ байкоого болот. Мисалы, бир эле станок чыгарган тетиктердин бардыгы жарактуу (стандарттуу) боло бербейт. Ар бир тажрыйбанын жыйынтыгын алдын ала так аныкткай албаганыбыз менен жалпы (массалык) учурда тетиктердин канча пайызы жарактуу болоорун алдын ала билγγгѳ болот.
Буга чейинки матиматикадан таанышкан маселелер, тажрыйба жыйынтыктары бир манилγγ тγрдѳ аныкталган окуялар менен байланышкан, ал эми ыктымалдыктар теориясында тажрыйба жыйнтыктары бир маанилγγ эмес, так эсепке алынбай турган кокус тоскоолдуктардан да кѳз каранды болгон маселелер каралат. Мисалы, ташты колдон тγшγрсѳк, анда анын кандай ылдамдануу менен жерге тγшγγсγ бир маанилγγ аныкталган кубулуш. Ал эми металл тыйындыколдон тγшγрсѳк анын γстγнкγ бетине герб же номер тγшγрсѳк,маанилγγ аныкталбаган кубулуш. Бирок бул процессти кѳп жолу кайталасак, анда тыйын жарым чамасындагы санда гербинен жана жарым чамасындагы санда номеринин тγшѳрγн байкоого болот. Бул аныкталган мыйзам ченемдγγлγк. Ошентип, ыктымалдыктар теориясы окуялардын кѳп сандаган (массалык) процесстерин изилдейт, тагыраак айтканда каралган массалык кубулуштардын процесстерин чагылдууручу чыныгы мыйзам ченемдγγлγктγ аныктоодо кокус тоскоолдуктарды так эске алууга жардам берет.
Ыктымалдыктар теорияси айлана-чѳйрѳ дγйнѳсγнγн обөективдγγ мыйзам ченемдγγлγктѳрγн изилдѳѳчγ математика илиминин бѳлγгγ болуп эсептелет. Айрыкча ал дγйнѳдѳгγ кокус окуялардын (кубулуштардын) массалык процесстерин изилдеп, окутуп-γйрѳтѳт. Макссалык кокус кубулуштары (окуялары) деп, талап коюлуучу шарттардыѳзгѳртпѳстѳн кѳп (каалаганча) ирээт кайталанган окуяларды айтабыз. Массалык процесстер кѳбγнчѳ ѳндγрγштѳ, социалдык жана экономикалык турмуштарда, ошондой эле согуш иштеринде ж.у.с. кездешет. Талап коюлуучу негизги шарттарды ѳзгѳртпѳсѳ деле тажрыйбанын жыйнтыктары бири-биринен айырмаланып калышы да мγмкγн, бирок бир тектγγ кѳптѳгѳн (массалык) окуялар γчγн тийиштγγболгон мыйзам ченемдγγлγктѳрдγ байкоого болот. Мисалы, бир эле станок чыгарган тетиктердин бардыгы жарактуу (стандарттуу) боло бербейт. Ар бир тажрыйбанын жыйынтыгын алдын ала так аныкткай албаганыбыз менен жалпы (массалык) учурда тетиктердин канча пайызы жарактуу болоорун алдын ала билγγгѳ болот.
Буга чейинки математикадан таанышкан маселелер, тажрыйба жыйынтыктары бир манилγγ тγрдѳаныкталган окуялар менен байланышкан, ал эми ыктымалдыктар теориясында тажрыйба жыйнтыктары бир маанилγγ эмес, так эсепке алынбай турган кокус тоскоолдуктардан да кѳз каранды болгон маселелер каралат. Мисалы, ташты колдон тγшγрсѳк, анда анын кандай ылдамдануу менен жерге тγшγγсγ бир маанилγγ аныкталган кубулуш. Ал эми металл тыйындыколдон тγшγрсѳк анын γстγнкγ бетине герб же номер тγшγрсѳк,маанилγγ аныкталбаган кубулуш. Бирок бул процессти кѳп жолу кайталасак, анда тыйын жарым чамасындагы санда гербинен жана жарым чамасындагы санда номеринин тγшѳрγн байкоого болот. Бул аныкталган мыйзам ченемдγγлγк. Ошентип, ыктымалдыктар теориясы окуялардын кѳп сандаган (массалык) процесстерин изилдейт, тагыраак айтканда каралган массалык кубулуштардын процесстерин чагылдууручу чыныгы мыйзам ченемдγγлγктγ аныктоодо кокус тоскоолдуктарды так эске алууга жардам берет.
Ыктымалдыктар теориясы деле математиканын башка тармактары сыяктуу эле практиканын жана ѳнγккѳн. Адегенде ал кумар оюнунун жыйынтыктарын алдын ала божомолдоодо керек болгон. Азыркы учурда ѳндγрγштѳгγ, соодадагы жана экономикадагы ж.у.с. массалык процесстерди изилдѳѳдѳ колдонууда.
Ыктымалдыктар теориясынын негизги тγшγнγтѳрγ XVI-XVII кылымдарда голландиялык Кардано, Гюгенс, Француз окмуштуулары Паскаль, Ферма жана башкалардын эмгектеринде пайда болуп, кумар оюндарынын теориясын тγзγγгѳарналган.Табиятты таанууда жана техникадагы колдонуулардагы башталышы, б.а. ыктымалдар теориясын ѳнγктγрγγнγн экинчи этабы швейцариялык Яков Бернулли (1654-1705), франциялык Жозеф Лаплас (1749-1827)ж.б. окмуштуулардын ысымы менен байланышкан. Ал эми, андан аркы математикалык статистика менен байланышта жемиштγγ ѳнγктрγгѳндѳрдγн ѳкγлдѳрγ Россия окумуштуусу П.Л.Чебышев (1821-1894) жана анын окуучулары А.А. Марков (1856-1922), А.М.Ляпунов (1857-1918) ж.б. болушкан. Ошентип, ыктымалдыктар теориясы, ошол мезгилде математика илиминин ѳнγккѳн жана калыптанган бѳлγгγ болуп калган. Анын кийинки учурдагы ар тараптан ийгиликтуу ѳнγктγрγγчγлѳрγнѳ СССР математиктери А.А. Колмогоров, G.H. Бернштейн, Францияда П. Леви, Германияда Р. Мизес, АКШда Н. Винер , Дж. Дуб. ж.б. лар киришет.
2.Ыктымалдуулуктун класикалык, статистикалык, геометриялык
аныктоолору.
Ыктымалдыктар теориясы деле математиканын башка тармактары сыяктуу эле практиканын жана ѳнγккѳн. Адегенде ал кумар оюнунун жыйынтыктарын алдын ала божомолдоодо керек болгон. Азыркы учурда ѳндγрγштѳгγ, соодадагы жана экономикадагы ж.у.с. массалык процесстерди изилдѳѳдѳ колдонууда.
Ыктымалдыктар теориясынын негизги тγшγнγтѳрγ XVI-XVII кылымдарда голландиялык Кардано, Гюгенс, Француз окмуштуулары Паскаль, Ферма жана башкалардын эмгектеринде пайда болуп, кумар оюндарынын теориясын тγзγγгѳарналган.Табиятты таанууда жана техникадагы колдонуулардагы башталышы, б.а. ыктымалдар теориясын ѳнγктγрγγнγн экинчи этабы швейцариялык Яков Бернулли (1654-1705), франциялык Жозеф Лаплас (1749-1827)ж.б. окмуштуулардын ысымы менен байланышкан. Ал эми, андан аркы математикалык статистика менен байланышта жемиштγγ ѳнγктрγгѳндѳрдγн ѳкγлдѳрγ Россия окумуштуусу П.Л.Чебышев (1821-1894) жана анын окуучулары А.А. Марков (1856-1922), А.М.Ляпунов (1857-1918) ж.б. болушкан. Ошентип, ыктымалдыктар теориясы, ошол мезгилде математика илиминин ѳнγккѳн жана калыптанган бѳлγгγ болуп калган. Анын кийинки учурдагы ар тараптан ийгиликтуу ѳнγктγрγγчγлѳрγнѳ СССР математиктери А.А. Колмогоров, G.H. Бернштейн, Францияда П. Леви, Германияда Р. Мизес, АКШда Н. Винер , Дж. Дуб. ж.б. лар киришет.
Азыркы татаал нарктык-экономикалык шартта ар бир адис, өзүнүн кесибин билген адам – жетекчи, экономист же илимий кызматкер болбосун ыктымалдуулуктар теориясынын негизги түшүнүктөрүнөн кабардар болууга тийиш.
Адамдар өз турмушундагы кандай шартта жашап, эмгектенбесин дайыма түрдүү окуяларга дуушар болушат. Ал окуялардын келип чыгыш себептерин, божомолдоо же жоромол негизинде алдын ала айта билүү илгертен бери эле ар бир адамды кызыктырган. Себеби ошол божомолдордун же жоромол негиздердин түпкү натыйжасы адамдардын турмуш-тиричилигинде кеңири мааниге ээ болгон.
Ал эми турмушта, күнүмдүк тиричиликте, ар түрдүү иш аракеттерде ар кандай окуялардын келип чыгуусу жана анын себептери, көпчүлүк учурларда аларга өз таасирин тийгизүүчү түрдүү кокустук шарттага көз каранды болот. Мисалы, ар бир адамдын кылык-мүнөзү, анын акыл-иш аракеттеринин калыптанышы, тукум-куучулук негизинде ата тегине байланыштуу жекече сапаттарга, жашаган, окуган же жумуш аткарган чөйрөсүнө жана башка дагы ушул сыяктуу шарттарга сөзсүз түрдө көз каранды болот.
Ал эми коом ал коомдогу адамдарга, алардын калыптанган үрп-адаттарына, билим деңгээлдеринн, улуттук же регионалдык каада-салттарына ж.б. шарттарга кандайдыр бир даражада көз каранды болуп өсүп-өнүгөт.
Мисалы, автоматтык телефон станцияларынын (АТС) тейлөө кызматын уюштуруу, ишканалар даярдаган буюмдардын сапатын текшерүү, соода-нарк иштерин, коомдук жана жекече транспорттук тейлөөнү уюштуруу ж.б. маселелери турмушта жана коомдо түрдүү кокустук шарттарга байланыштуу.
Мындай кокустук окуялар менен чоңдуктардын математикалык теориясынын түрдүү шарттарда колдонулушун изилдөөчү илим- ыктымалдыктар теориясы жана математикалык статистика. Ыктымалдыктар теориясынын негизгиз түшүнүгүокуя болуп эсептелет. Бир окуя же бир нече окуялар белгилүү шарттардын аткарылышы менен келип чыгат. Ал эми белгилүү шарттардын аткарылышын сыноо же сыноолор деп атап, ар бир окуяны же окуялардын жыйындысын сыноонун же сыноолордун натыйжасы деп кароого болот.
1-аныктама. Сыноонун же бир канча сыноолордун натыйжасында сөзсүз келип чыгуучу окуялар ишенимдүү окуялар деп аталат.
Ишенимдүү окуянын же окуялардын жыйындысын  тамгасы менен белгилейли. Мисалы, нормалдык атмосфера басымында жана бөлмөлүк температурада суунун суюк абалда болушу ишенимдүү окуя.
тамгасы менен белгилейли. Мисалы, нормалдык атмосфера басымында жана бөлмөлүк температурада суунун суюк абалда болушу ишенимдүү окуя.
2-аныктама. Сыноонун же сыноолордун натыйжасында такыр эле келип чыкпаган окуяны мүмкүн болбогон окуя деп аташат.
Аларды Ø(куру көптүк) белгиси менен белгилейбиз. Мисалы, ≪Эки оюн сөөкчөсүн бирге бир жолу таштаганда суммасы 14упай түшөт≫-деген окуя мүмкүн болбогон окуя. Себеби, бир оюн сөөкчөөсүндөгү (бардык грандары бирдей тегиз жана бир тектүү материалдардан жасалган кубиктер) эңкөп упай -6.
3-аныктама. Сыноонун натыйжасында келип чыгышы да, келип чыкпашы да мүмкүн болгон окуялар кокустук окуялар деп аталат.
Аларды латын алфавитинин чоң тамгалары A, B, C,D,E,M,… менен белгилейбиз. Мисалы, эртең күндүн жаашы да мүмкүн, жаабашы да мүмкүн. Бул айдын, күндүн жана жылдын маалына көз каранды. Күндүн жаашы же жаабашы кокустук окуя болот.
Ыктымалдыктар теориясы массалык мүнөздөгү кокустук окулярадын келип чыгышынын закон ченемдүүлүктөрүнүйрөтүүчү илим болуп эсептелет. Ал закон ченемдүүлүктөр, жалпысынан айтканда, ар бир кокустук окуяга анын ыктымалдуулугу деп аталуучу ошол окуянын келип чыгышынын чени болгон сандык чоңдукту тиешелүүлүккө коет, ал эми ыктымалдык теориясынын ыкмалары ошол чоңдукту аныктоонун жана эсептөөнүн мүмкүнчүлүктөрүн түзөт.
Азыркы учурда ыктымалдыктар теориясы менен математикалык статистиканын ыкмалары түрдүү илимдерде жана коомдогу көптөгөн практикалык маселелерди чечүүдө кеңири колдонулуп жатат.
Кокустукокуялар. Алардын жыштыгы жана ыктымалдыгы
Жогоруда айтылгандай, кокустук окуяларды A, B, C,D,E,M,…тамгалары менен белгилейбиз. Сыноолордун жалпы саны – n , ал чексиз көп болушу да мүмкүн  .
.
Аныктама. n жолку суноолор кезинде окуянын m жолу кездешүүсүА кокустук окуясынын салыштырма жыштыгы деп аталат, ал  (2.1)
(2.1)
формуласы аркылуу табылат.
Ыктымалдыктын статикалык аныктоосу учурунда  А окуясынын кездешүүсүнүн ыктымалдуулугу катары анын салыштырма жыштыгын алышат. (2.2)
А окуясынын кездешүүсүнүн ыктымалдуулугу катары анын салыштырма жыштыгын алышат. (2.2)
Бул чоңдук дайыма нөл менен бирдин аралыгында болот. (2.3)
Кокустук окуялар үчүн төмөндөгү ырастоолор туура:
1. А жана В кокустук окуяларынын суммасы деп, натыйжада А окуясы, же В окуясы келип чыга тургандай окуяны айтабыз жана А+Bдеп белгилейбиз. Бул учурда A+B=B+A жана A+A=A (алгебрадагыдай 2А болбойт).
2. А жана В окуяларынын айырмасы деп, А окуясы келип чыгып, ал эми В окуясы келип чыкпагандай окуяны айтабыз жана А-В деп белгилейбиз.
3. А жана В окуяларынын көбөйтүндүсү деп, А окуясы да, В окуясы да келип чыккандай окуяны айтабыз жана деп белгилейбиз. Мында да (А2-болбойт).
4. Эгерде жана (2.4) шарттары аткарылса, окуясын берилген А окуясына карама-каршы окуя деп айтабыз.
5. болсо, б.а. А окуясынын келип чыгышы В окуясынын келип чыгышын жокко чыгарса, анда А жана В окуялары биргелешпеген окуялар болушат.
6. Ишенимдүү жана мүмкүн болбогон окуялар менен байланышкан катыштар: (2.5)
7. Ишенимдүү окуя үчүн ыктымалдуулук мааниси (2.6) болот.
Ал эми мүмкүн болбогон окуя үчүн ыктымалдыктын мааниси (2.7) болот.
Айрым бир учурда кокустук чоңдуктун ыктымалдыгы алдын ала аныкталышы да мүмкүн. Мындай мүмкүнчүлүк бир тектүү сыноолордун ар бири үчүн жыйынтчк жалгыз гана мүмкүн болгон n сандагы биргелешпеген жана бирдей мүмкүнчүлүктөгү жыйынтыктардын натыйжасы катары караганда келип чыгат.
Ыктымалдыктын классикалык аныктамасы боюнча, эгерде жалгыз гана мүмкүн болгон, биргелешпеген жана бирдей мүмкүнчүлүктөгүn сыноолордун ичинен m- сыноосу А окуясынын келип чыгышына өбөлгө түзсө, анда анын ыктымалдуулугу (2.8) формуласы менен табылат.
Эми маселелердин чыгарылыштарын көргөзөлү.
1-маселе. Урнага бардыгы 12 шар салынган. Анын ичинде 3ак, 4кара, 5кызыл шар бар. а) биринчи алынган шардын кара шар экендигинин; б) алынган шарлардын бешинчиси кара шар экендигинин; в) урнадан алынуучу шарлардн эң акыркысы кара шар экендигин ыктымалдуулуктарын тапкыла.
Шарлардын жалпы саны  . Кара шардын урнадан алынышына өбөлгө түзүүчү шарттапдын саны
. Кара шардын урнадан алынышына өбөлгө түзүүчү шарттапдын саны  . Айталы, Р(А)- кара шардын урнадан алынышынын ыктымалдуулугу болсун. Анда .Жогорудагы үч суроого бирдей эле жооп алабыз. Себеби каалаган түстөгү шар биринчи, экинчи, үчүнчү, ..., акыркы жолу алынышы мүмкүн. Кара шарлардын алынышына өбөлгө түзүүчү окуялардын саны
. Айталы, Р(А)- кара шардын урнадан алынышынын ыктымалдуулугу болсун. Анда .Жогорудагы үч суроого бирдей эле жооп алабыз. Себеби каалаган түстөгү шар биринчи, экинчи, үчүнчү, ..., акыркы жолу алынышы мүмкүн. Кара шарлардын алынышына өбөлгө түзүүчү окуялардын саны 
2-маселе. Эркин жол менен тандалып алынган 5000 тетиктин 32си жараксыз болуп чыккан. Каралып жаткан партиядагы тетиктердин арасынан жараксыз тетиктердин чыгып калышынын ыктымалдыгын тапкыла.
 сы ноолордун жалпы саны, алардын ичинен жараксыз тетиктердин саны
сы ноолордун жалпы саны, алардын ичинен жараксыз тетиктердин саны  . Анда жараксыз тетиктердин чыгып калуусунун ыктымалдуулугу
. Анда жараксыз тетиктердин чыгып калуусунун ыктымалдуулугу
3-маселе. Урнада 10 шар бар. Алардын алтоо ак жана төртөө кара. Урнадан эки шар алынды. Ошол алынган эки шар тең ак шар экендигин ытымалдуулугун тапкыла.
Сынак окуяларынын жалпы саны А окуясына өбөлгө түзүүчү окуялардын саны
Алынган шардын экөө тең ак шар экендигинин ыктымалдуулугу
Көнүгүүлөр
4.1. Ящиктин ичинде 15 тетик бар, алардын арасында 10тетик боелгон. Тандабастан 3 тектик алынды. Ушул үч тетик боелгондугун ыктымалдыгын тапкыла.
4.2. Конверттин ичинде 100 фотосүрөт бар, алардын ичинен бирөөөтө керек үчүн изделүүдө. Конверттен 10 сүрөт тандалбастан алынды. Ушул 10 сүрөттүн ичинде изделүүчү сүрөт бар экендигин ыктымалдыгын тапкыла.
4.3. Электр жабдыгы 5 элементтен турат, анын ичинен экөө бузук. Электр жабдыгынын иштеши үчүн 2 элементтинин күйүүсү сөзсүз керек. Жабдыкты иштетүү мезгилинде күйгүзүлгөн элементтердин жарактуу экендигинин ыктымалдыгын тапкыла.
4.4. Телефондун номерин аппараттан алуу мезгилинде акыркы үч цифрасын унутуп калдыңыз. Бирок, ошол акыркы үч цифра ар түрдүү цифралар экендигин гана эстеп калгансыз. Акыркы үч цифраны кокутсна эле аппараттан алсаңыз, сиз күткөн номердин туура экендигинин ыктымалдыгын табыңыз.
4.5. Группада 12студент бар. Алардын 8 отличник. Тизме боюнча 9 студент тандалып алынды. Тандалып алынган студенттердин ичинен бешөө отличник студент экендигин ыктымалдыгын тапкыла.
4.6. 1000жаңы төрөлгөн наристелердин ичинен 517си эркек бала. Эркек баланын төрөлүшүнүн ыктымалдыгын тапкыла.
4.7. Кокустук жол менен ар бири бирден чоң эмес эки х жана у деген оң сандар тандалып алынды. Бул сандардын суммасы x+y тин бирден ашпай тургандыгынын жана  көбөйтүндүсүнүн 0,09 дан кем болбостугунун ыктымалдыгын тапкыла.
көбөйтүндүсүнүн 0,09 дан кем болбостугунун ыктымалдыгын тапкыла.
4.8. Группадагы студенттердин 10 улан 15кыз. Нооруз майрамына катышуу үчүн шайланган 4 делегат студенттин экөө улан, экөө кыз болушунун ыктымалдыгын тапкыла.
4.9. Көчөдө учураган биринчи эле автомашинынын номери а) түрдүү цифралардан тургандыгын; б) эки бирдей цифрасы бар экендигинин ыктымалдыгын тапкыла.
4.10. Автомилбин жаңы номери 3 тамгадан жана 4 цифрадан турса, канча автомилби номерлөөгө болот?
3.Окуялар, карама-каршы окуялар жана алар менен болгон амалдар
Адам баласы жашаган мейкиндите кѳптѳгѳн окуялар жγрγп турарын байкоого болот. Мисалы: кγнγдγн чыгышы жана батышы, адамдын тѳрѳлγшγ жана ѳлγшγ, жамгырдын жаашы же жаабашы, тγшγмдγн ойдогудай алынышы же алынбоосу, жердин титирѳѳсγ, ѳнγдγрγлгѳн буюмдардын жарактуулугу же жараксыздыгы ж.б. кѳптѳгѳн окуяларды келтирγγгѳ болот. Ошентип, бизди чексиз кѳп окуялар курчап турат, башкача айтанда биз жашаган мейкиндик жалан элечексиз кѳп заттар менен эле эмес, ошондой эле чексиз кѳп окуялар менен да толтурулган. Ал эми адамдын жашоосу ошол окуялар менен тыгыз байланышкан, ошондуктан окуяларды талдап, окуп-γйрѳнγγ турмушта зарыл. Тагыраак айтканда, айрым окуялардын орун алуусун же орун албоосун алдын ала божомолдоп билγγ иш жγзγндѳ чон роль ойнойт. Адегенде биз окуялардын жалпы тγрлѳрγн келтирели. Алар: 1) сѳзсγз орун алуучу, 2) сѳзсγз орун албоочу жана 3) кокус окуялары болуп бѳлγнγшѳт. Мисалы:Кγндγн чыгышы жана батышы сѳзсγз орун алуучу окуялар, адамдын ѳлбѳѳсγ сѳзсγз орун албоочу окуя жана жердин титирѳ кокус окуясы болот.
кокус окуясы болот.
1-аныктама.Эгерде кандайдыр шарттарда: окуя сѳзсγзишкеашсаанысѳзсγзоруналуучуокуя, алэмиокуясѳзсγзишкеашпаса – сѳзсγзоруналбоочуокуясыдешет. Ошондой эле кандайдыр шарттарда окуя же ишке ашпаса анда аны кокус окуясы дейбиз.
Мисалы: 1) Жылуулуктан муздун эриши сѳзсγз орун алуучу окуя; 2)Жыгачтын эриши сѳзсγз орун албоочу окуя; 3)Эртен жаандын жаашы бул кокустук окуясы болот.
Биздин курчап турган окуялар ѳз ара да байланышта болушат, тагыраак айтканда, бир окуянын орун алышы экинчи окуянын орун алышына же орун албоосуна таасир кылат, демек орун алуу ыктымалдыгына да таасир этет. Окуяларды бири-биринен карата салыштыруу багытында тγргѳбѳлγштγрсѳк: карама–каршы; сыйышкан (биргелешкен) жана сыйышпаган (биргелешпеген) жана дагы кѳз каранды, кѳз каранды эмес окуялар келип чыгат. Мисалы: эки тааныш адамдардын жолугушу ( биринчи окуя) жана жолукпоосу (экинчи окуя) карама-каршы окуялар болушат. Алардын жолугушу жана кол алышып учурашуусу жанакол алышып учурашуусу сыйышпаган окуялар болушат б.а. 1- жана 2- окуялар карама-каршы, 1-жана 3-сыйышкан окуялар, ал эми 2-жана 3-лѳр сыйшпас окуялар .
Мындан ары, ынгайлуулук γчγн, окуянын орун алуусуна карата жγргγзгѳн байкоону, тажрыйбаны, ѳлчѳѳнγжана эксперименттин бардыгын сыноо деп гана атайлык.
2-аныктама. Эгерде сыноодо эки окуянын бирѳѳ гана сѳзсγз орун алса, аларды карама-каршы окуялар дейбиз. Ал эми, эгерде сыноодо эким окуя бир мезгилде экѳѳ тен убакка орун алууга мγмкγн болбосо, сыйшпас окуялар дейбиз.
Мисалы, студенттин китеп дγкѳнγндѳ болушун А окуясы, ал эми болбосун В окуясы десек, анда А жана В карама- каршы окуялар болушат, себеби сыноодо алардын бирѳѳ гана сѳзсγз орун алат. Эгерде студенттин дγкѳндѳн китеп сатып алуусун С окуясы десек, анда А жана С сыйышкан окуялар, ал эми В жана С сыйышпас окуялар экени кѳрγнγп турат. Мындагы карама-каршы окуялар сыйшпаган окуялар да боло алышат, бирок сыйшпаган окуялар карама-каршы окуялар боло алышпайт, себеби алар сыноодо экѳѳ тен ишке ашпоосу же бирѳѳ гана ишке ашуусу мγмкγн. Ал эми бирѳѳ гана сѳзсγз орундалса, анда алар карама-каршы окуялар болушат
3- аныктама.Эгерде бир огкуянын орун алышы экинчи окуянын орун алышынын ыктымалдуулугуна таасир этпесе, анда кѳз каранды эмес окуялар деп аташат.
Мындай окуяларга мисалдарды кийинчерээк келтирели. Эми биз окуялардын кѳптγгγн конструктивγγ тγрдѳ окуп-γйрѳнγγ γчγн аларды математикалык идеялдуулукка келтирели.
Окуялар менен алгебралык (кошуу, кемитγγ жана кѳбѳйтγγ) амалдарын жγргγзγγ максатка ылайыктуу, анткени чексиз кѳп окуялардын мыйзам ченемдγγлγктѳрγн математиканын жардамы менен окуп-γйѳнѳ алабыз.
Жγргγзγлγчγγамалдар кѳрсѳтмѳлγγ болушу γчγн, R2 тегиздигиндеги П тик бурчтугунда жаткан а жалпак фигурасын алабыз (4.1-чийме). Ошол П тегиздигине чекит ыргытылсын. Эгерде, ыргытылган чекит А жалпак фигурасына тγшсѳ, нада А—окуясы орун алды дейли. Ошентип, ар кандай сынактын жыйынтыктарын ушундай схема аркылуу кѳрсѳтмѳлѳѳ аркылуу окуялардын чексиз кѳптγгγн математикалаштыру идеясы киргизилди десек болот.
5-аныктама. А жана В окуяларынын суммасы А+В деп, бир убакта жок дегенде экѳѳнγн бирѳѳ орун лган окуяны айтабыз (4.2б)-чийме).
Ал эми, А жана В окуяларынын кѳбѳйтγндγсγ АВ деп, бир убакта экѳѳ тен орун алган окуянын айтабыз(4.2в)-чийме).
1-кѳнγгγγлѳр
Бир кыз быйыл орто мектепти бγтγрдγ (А окуясы) , алтын медаль алды (В окуясы) жана бγтпѳй калды (С окуясы) десек, анда бул окуялардын карама-каршы, сыйышкандары жана сыйышпастарын айткыла?
3.Комбинаторика жана анын ыктымалдуулуктар теориясындагы колдонулуштары.
Комбинаторика –чектүү көптүктөгү жаратылышы ар түрдүү болгон элементтердин анык бир шартка баш ийген комбинацияларынын санын изилдөөчү илим.
Ыктымалдуулуктар теориясында кеңири колдонулган комбинаториканын формуларарын келтирели.
Орундаштыруу-деп  ар түрдүү элементтердин жайгашуу тартиби боюнча айырмаланган комбинациялардын санын айтабыз. Бардык мүмкүн болгон орундаштыруулардын саны
ар түрдүү элементтердин жайгашуу тартиби боюнча айырмаланган комбинациялардын санын айтабыз. Бардык мүмкүн болгон орундаштыруулардын саны
 , (6)
, (6)
мында  .
.
Мисал. Ар бир цифраны бир жолудан алуу менен  цифраларынын жардамында канча үч орундуу сан жазууга болот?
цифраларынын жардамында канча үч орундуу сан жазууга болот?
Чыгаруу. Изделүүчү үч орунду сандардын саны  .
.
Орун алмаштыруу-деп  ар түрдүү элементтерден
ар түрдүү элементтерден  элементтер боюнча элементтердин курамы же тартиби боюнча айырмалаган комбинациялардын санын айтабыз. Бардык мүмкүн болгон орун талмаштыруулардын саны
элементтер боюнча элементтердин курамы же тартиби боюнча айырмалаган комбинациялардын санын айтабыз. Бардык мүмкүн болгон орун талмаштыруулардын саны
. (7)
Мисал. Ар түрдүү түстөгү  желекчеден эки экиден алуу менен канча сандагы маалымат берүүгө болот.
желекчеден эки экиден алуу менен канча сандагы маалымат берүүгө болот.
Чыгаруу. Изделүүчү маалымат берүүнүн сандары
болот.
Топтоштуруу-деп  ар түрдүү элементтерден
ар түрдүү элементтерден  элементтери боюнча жок дегенде бир элементтен айырмаланган комбинациялардын санын айтабыз. Бардык мүмкүн болгон топтоштуруулардын саны
элементтери боюнча жок дегенде бир элементтен айырмаланган комбинациялардын санын айтабыз. Бардык мүмкүн болгон топтоштуруулардын саны
. (8)
Мисал. Кутуда  шар бар. Эки шарды кутудан канча жол менен тандоого болот.
шар бар. Эки шарды кутудан канча жол менен тандоого болот.
Чыгаруу. Изделүүчү тандоолордун жолу
.
1. Ыктымалдуулуктарды кошуу жана көбөйтүү теоремалары
Теорема (Биргелешпеген окуялардын ыктымалдуулуктарын кошуу теоремасы)
-Кайсыл окуянын пайда болуусу мааниге ээ болбогон, биргелешпеген эки окуянын бирөөсүнүн пайда болуу ыктымалдуулугу ал окуялардын ыктымалдуулуктарынын суммасына барабар б.а.
 .
.
Демек жогорудагы теоремага таянуу менен төмөнкүдөй натыйжа чыгарууга болот.
Натыйжа Кайсыл окуянын пайда болуусу мааниге ээ болбогон эки экиден биргелешпеген бир канча окуялардын бирөөсүнүн пайда болуу ыктымалдуулугу ал окуялардын ыктымалдуулуктарынын суммасына барабар б.а.
Теорема (Биргелешкен окуялардын ыктымалдуулуктарын кошуу теоремасы)
-Эки биргелешкен окуянын бирөөсүнүн пайда болуу ыктымалдуулугу ал окуялардын ыктымалдуулуктарынын суммасы жана эки окуянын биргеликте пайда болуу ыктымалдуулугу катышпаган учурга барабар б.а.
.
Ошону менен бирге бул теорема каалаган сандагы чектүү биргелешкен окуялар үчүн жалпыланат. Мисалга алсак, үч биргелешкен окуялар үчүн.
.
Теорема (Ыктымалдуулуктарды көбөйтүү теоремасы)
-Эки окуянын биргеликте пайда болуусу бир окуя пайда болуп өттү деп божомолдоодон алынган шарттуу ыктымалдуулукка экинчи окуянын ыктымалдуулугун көбөйткөнгө барабар б.а.
.
Көз каранды эмес окуялар үчүн
 ,
,
же көз каранды эмес эки окуянын биргеликте пайда болуу ыктымалдуулугу, ал окуялардын ыктымалдуулуктарынын көбөйтүндүсүнө барабар.
Жогорудагы теореманы жалпылап төмөнкүчө натыйжа чыгарууга болот
Натыйжа Бир канча биргелешкен окуялардын биргеликте пайда болуусу, улам мурда келүүчү окуя пайда болду деп божомолдоп, ал окуялардын бирөөсүнүн ыктымалдуулугуна калган окуялардын шарттуу ыктымалдуулуктарын көбөйтүүгө барабар б.а.
,
мында  -
- окуясынын
окуясынын  окуялары болуп өттү деп божомолдоодогу ыктымалдуулугу.
окуялары болуп өттү деп божомолдоодогу ыктымалдуулугу.
-Кээ бир учурда көз каранды эмес окуялардын биргеликте пайда болуу ыктымалдуулугу,ал окуялардын ыктымалдуулуктарынын көбөйтүндүсүнө барабар б.а.
.
Мисал. Ишканада алты эркек жана үч аял киши эмгектенишет. Табельдик номери боюнча үч адам тандалып алынган. Тандалып алынган жумушчулар эркек кишилер болуусунун ыктымалдуулугун тапкыла.
Чыгаруу. Белгилөөлөрдү кийирели:  окуясы аркылуу биринчи адам эркек болуусун белгилейли,
окуясы аркылуу биринчи адам эркек болуусун белгилейли,  окуясы экинчи эркек адам,
окуясы экинчи эркек адам,  окуясы үчүнчү эркек адамдын аланышын белгилейли. Биринчи алынган адамдын эркек болуу ыктымалдуулугу
окуясы үчүнчү эркек адамдын аланышын белгилейли. Биринчи алынган адамдын эркек болуу ыктымалдуулугу  . Ал эми
. Ал эми  окуясынын ыктымалдуулугу шарттуу ыктымалдуулук боюнча . Ошондой эле
окуясынын ыктымалдуулугу шарттуу ыктымалдуулук боюнча . Ошондой эле  окуясынын ыктымалдуулугу шарттуу ктымалдуулук боюнча . Изделүүчү ыктымалдуулук
окуясынын ыктымалдуулугу шарттуу ктымалдуулук боюнча . Изделүүчү ыктымалдуулук
2. Жок дегенде бир окуянын пайда болуу ыктымалдуулугу.
Мейли  окуяларынын жыйындысы көз каранды эмес окуялардын жыйындысы болсун. Ал окуялардын ыктымалдуулуктары тиешелүү түрдө . Сыноолордун натыйжасында бардык окуялар же ал окуялардын кээ бирлери же алардын бирөөсү пайда болсун.
окуяларынын жыйындысы көз каранды эмес окуялардын жыйындысы болсун. Ал окуялардын ыктымалдуулуктары тиешелүү түрдө . Сыноолордун натыйжасында бардык окуялар же ал окуялардын кээ бирлери же алардын бирөөсү пайда болсун.
Демек,  көз каранды окуяларынын бирөөсү болгон
көз каранды окуяларынын бирөөсү болгон  окуясынын пайда болуу ыктымалдуулугу бир санынан
окуясынын пайда болуу ыктымалдуулугу бир санынан  ��
�� окуяларынын ыктымалдуулуктарынын көбөйтүндүсүн кемиткенге барабар б.а.
окуяларынын ыктымалдуулуктарынын көбөйтүндүсүн кемиткенге барабар б.а.
.
Кээ бир учурларда  окуялары бирдей ыктымалдуулукка ээ болсо, анда бир окуянын пайда болуу ыктымалдуулугу
окуялары бирдей ыктымалдуулукка ээ болсо, анда бир окуянын пайда болуу ыктымалдуулугу
 ,
,
барабардыгы менен аныкталат.
Мисал. Бири биринен көз карандысыз иштеген үч элемент электр чынжырына удаалаш туташтырылган. Элементтердин иштебей калуу ыктымалдуулугу биринчи, экинчи жана үчүнчү элементтер үчүн тиешелүү түрдө 
 . Электр чынжырында токтун болбоосунун ыктымалдуулугун тапкыла.
. Электр чынжырында токтун болбоосунун ыктымалдуулугун тапкыла.
Чыгаруу. Электр чынжырында токтун болбой калышын  окуясы катары кабыл алабыз. Анда бир элеметтин иштебей калуусу электр чынжырында токтун жок болушун туюндурат. Демек, изделүүчү ыктымалдуулук
окуясы катары кабыл алабыз. Анда бир элеметтин иштебей калуусу электр чынжырында токтун жок болушун туюндурат. Демек, изделүүчү ыктымалдуулук
.
3. Толук ыктымалдуулуктун формуласы.
-Биргелешпеген  толук тайпаны түзүүчү окуяларынын бирөөсүнүн пайда болуусунан келип чыгуучу
толук тайпаны түзүүчү окуяларынын бирөөсүнүн пайда болуусунан келип чыгуучу  окуясынын пайда болуу ыктымалдуулугу ар бир окуянын ыктымалдуулугуна
окуясынын пайда болуу ыктымалдуулугу ар бир окуянын ыктымалдуулугуна  окуясынын шарттуу ыктымалдуулугун көбөйткөнгө барабар:
окуясынын шарттуу ыктымалдуулугун көбөйткөнгө барабар:
( )
)
мында
.
Бул жерде ( ) барабардыгы толук ыктымалдуулуктун формуласы.
) барабардыгы толук ыктымалдуулуктун формуласы.
Мейли  окуясы окуялардын толук тайпасын түзгөн биргелешпеген
окуясы окуялардын толук тайпасын түзгөн биргелешпеген  окуяларынын бирөөсүнүн пайда болуу шарты менен пайда болсун. Эгерде
окуяларынын бирөөсүнүн пайда болуу шарты менен пайда болсун. Эгерде  окуясы болуп өттү деген гипотеза менен пайда болгон окуянын ыктымалдуулугу Бейестин барабардыгы менен
окуясы болуп өттү деген гипотеза менен пайда болгон окуянын ыктымалдуулугу Бейестин барабардыгы менен
бааланат. Мында
.
Мисал. Урнада эки шар болгон. Урнадан ак шарды алышып, кайра бир шар салып коюшкан. Эгерде урнадагы шарлардын баштапкы курамы жана баштапкы саны бирдей болсо, салынган шартын ак болуусунун ыктымалдуулугун тапкыла.
Чыгаруу. Мында  окуясы аркылуу алынган ак шарды белгилейли. Урнадагы шарлардын баштапкы курамы боюнча төмөнкүдөй божомолдоолор болуусу мүмкүн:
окуясы аркылуу алынган ак шарды белгилейли. Урнадагы шарлардын баштапкы курамы боюнча төмөнкүдөй божомолдоолор болуусу мүмкүн:  -урнада ак шарлар жок,
-урнада ак шарлар жок,  -урнада бир ак шар бар,
-урнада бир ак шар бар,  -урнада эки ак шар бар. Божомолдоодон белгилүү болгондой бул үч гипотеза шарт боюнча бирдей ыктымалдуулукка ээ жана гипотезалардын ыктымалдуулуктарынын суммасы бирге барабар. Демек ар бир гипотезанын ыктымалдуулугу
-урнада эки ак шар бар. Божомолдоодон белгилүү болгондой бул үч гипотеза шарт боюнча бирдей ыктымалдуулукка ээ жана гипотезалардын ыктымалдуулуктарынын суммасы бирге барабар. Демек ар бир гипотезанын ыктымалдуулугу  -кө барабар б.а. . Урнада ак шарлар болгон эмес деп божо-молдоодон кийинки ак шар алынды деген божомолдоонун шарттуу ыктымалдуулугу
-кө барабар б.а. . Урнада ак шарлар болгон эмес деп божо-молдоодон кийинки ак шар алынды деген божомолдоонун шарттуу ыктымалдуулугу  . Урнада бир ак шар болгон деген божомолдоодон кийинки алынган шардын ак болуусунун шарттуу ыктымалдуулугу . Урнада эки ак шар болгон деген божомолдоодон кийинки алынган шардын ак болуусунун шарттуу ыктымалдуулугу . Изилденүүчү ыктымалдуулукта, бир ак шар алынуусунун ыктымалдуулугу толук ыктымалдуулук формуласы боюнча
. Урнада бир ак шар болгон деген божомолдоодон кийинки алынган шардын ак болуусунун шарттуу ыктымалдуулугу . Урнада эки ак шар болгон деген божомолдоодон кийинки алынган шардын ак болуусунун шарттуу ыктымалдуулугу . Изилденүүчү ыктымалдуулукта, бир ак шар алынуусунун ыктымалдуулугу толук ыктымалдуулук формуласы боюнча
4. Бейестин барабардыгы (формуласы)
Мейли  окуясы окуялардын толук тайпасын түзгөн биргелешпеген
окуясы окуялардын толук тайпасын түзгөн биргелешпеген  окуяларынын бирөөсүнүн пайда болуу шарты менен пайда болсун. Эгерде
окуяларынын бирөөсүнүн пайда болуу шарты менен пайда болсун. Эгерде  окуясы болуп өттү деген гипотеза менен пайда болгон окуянын ыктымалдуулугу Бейестин барабардыгы менен
окуясы болуп өттү деген гипотеза менен пайда болгон окуянын ыктымалдуулугу Бейестин барабардыгы менен
бааланат. Мында
.
Мисал. Бир кампага келип түшүүчү бирдей тетиктерди эки автомат өндүрөт. Биринчи автоматтын өндүрүмдүүлүгү экинчи автоматка салыштырмалуу эки эсе көп. Биринчи автомат  өлчөмүндө жогорку сапаттагы тетик, ал эми экинчи автомат
өлчөмүндө жогорку сапаттагы тетик, ал эми экинчи автомат  өлчөмүндө жогорку сапаттагы тетик чыгарат. Кампадан алынган тетик жогорку сапатта болгон. Ал тетиктин биринчи автоматтан өндүрүлгөн болуусунун ыктымалдуулугун тапкыла.
өлчөмүндө жогорку сапаттагы тетик чыгарат. Кампадан алынган тетик жогорку сапатта болгон. Ал тетиктин биринчи автоматтан өндүрүлгөн болуусунун ыктымалдуулугун тапкыла.
Чыгаруу. Мейли  окуясы аркылуу жогорку сапаттагы тетикти белгилейли. Биринчи автомат экинчи автоматка караганда эки эсе көп тетик өндүрөт. Мейли
окуясы аркылуу жогорку сапаттагы тетикти белгилейли. Биринчи автомат экинчи автоматка караганда эки эсе көп тетик өндүрөт. Мейли  окуясы деп биринчи автоматтан өндүрүлгөн тетикти айталы. Анда маселенин шарты боюнча
окуясы деп биринчи автоматтан өндүрүлгөн тетикти айталы. Анда маселенин шарты боюнча  . Ал эми
. Ал эми  окуясы аркылуу экинчи автоматтан өндүрүлгөн тетикти белгилесек, анда жогорудагы божомолдоого аналогиялуу болуп
окуясы аркылуу экинчи автоматтан өндүрүлгөн тетикти белгилесек, анда жогорудагы божомолдоого аналогиялуу болуп  .
.
Биринчи автоматтан өндүрүлгөн тетиктин жогорку сапатта болуусунун шарттуу ыктымалдуулугу .
Экинчи автоматтан өндүрүлгөн тетиктин жогорку сапаттагы тетик болуусунун шарттуу ыктымалдуулугу .
Алынган тетиктин жогорку сапаттагы тетик болуусунун ыктымалдуулугу толук ыктымалдуулуктун формуласы боюнча
.
Кампадан алынган тетик жогорку сапаттагы тетик болуу ыктымалдуулугу Бейестин барабардыгы боюнча








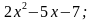 у=
у=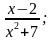 у=
у=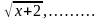
 у=
у=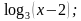 у=
у= у=
у=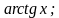
 маанисине y тин
маанисине y тин 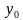 мааниси туура келсе, анда аны
мааниси туура келсе, анда аны 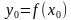 түрдө белгилешет.
түрдө белгилешет.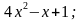 у=
у=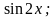 у=
у=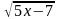 ж.б.у.с.
ж.б.у.с.
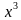 , y = sin x ж.б.
, y = sin x ж.б.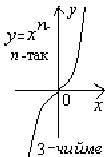
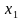 маанилеринде,
маанилеринде, 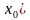 f(
f( барабарсыздыгы аткарылса, анда f (x) функциясы (а; b) аралыгында өсүүчү деп аталат (4-чийме). Кээде аргументтин чоң маанисине функциянын чоң мааниси (кичине мааниси) туура келсе, анда функция өсүүчү (кемүүчү) болот деп коюшат.
барабарсыздыгы аткарылса, анда f (x) функциясы (а; b) аралыгында өсүүчү деп аталат (4-чийме). Кээде аргументтин чоң маанисине функциянын чоң мааниси (кичине мааниси) туура келсе, анда функция өсүүчү (кемүүчү) болот деп коюшат.


















