Содержание.
I. Введение. 2
II. ДОЛГАЯ ЖИЗНЬ МЫЛЬНОГО ПУЗЫРЯ. 3
2.1. Исторический очерк. 3
2.2. Недолговечность мыльного пузыря? 3
2.3. Самый большой пузырь 3
2.4 Пузыри в биологии. 4
2.5. Пузыри в нефтеперерабатывающей промышленности. 5
III. Теория мыльных пузырей. Физические явления и их объяснение. 6
3.1. Монослой на поверхности воды. Адсорбция. 6
3.2. Внутреннее устройство мыльного пузыря 7
3.3. Задача о предельном радиусе пузыря 8
3.4. Форма пузыря. 9
3.5. Взаимное притяжение соприкоснувшихся мыльных пузырей. 10
3.6. Элементарная теория разрушения пузыря. 11
3.7. Оптика мыльного пузыря. 13
IV. Практическая часть. 18
4.1.Кристаллизация мыльного пузыря 18
4.1.1 Вращение. 18
4.1.2. Постепенность замерзания. 18
4.1.3. Механические свойства. 19
4.1.4. Вмятина. 20
4.1.5. Тонкий пузырь. 20
4.1.6. Влияние глицерина. 21
4.1.7. Снежинка как центр кристаллизации. 21
V. Заключение. 22
VI. Литература 23
VII. Приложение. Фотографии. 24
I.Введение.
В нем столько блеску было,
Была такая спесь,
А он- воды и мыла
Раздувшаяся смесь.
Самуил Маршак "Мыльные пузыри"
Эта работа посвящена мыльным пузырям. Почему я выбрала эту тему? Во - первых, мыльные пузыри - это очень красиво , неслучайно их так любят дети , и не только дети. "Мыльный пузырь, пожалуй, самое восхитительное и самое изысканное явление природы" Марк Твен.
Во-вторых, их очень просто сделать. Физика - это наука о сравнительно простых моделях, поддающихся описанию, которые с той или иной степенью точности позволяют описывать и прогнозировать сложнейшие явления природы
Мыльные пузыри позволяют понять как общие законы физики себя обнаруживают в конкретных, иной раз неожиданных явлениях.
В-третьих, как выяснилось в процессе работы, изготовление и изучение мыльных пузырей позволяет исследовать, продемонстрировать, "прочувствовать" множество физических законов, которые имеют важнейшее значение в науке и технике. К ним относятся: свойства жидкостей, поверхностная энергия (моющие растворы); плавание в жидкостях и газах (летательные и подводные аппараты); физические свойства и методы получения тонких пленок (широчайший спектр применения от производства полупроводниковых микросхем, а следовательно "железная" основа информационных технологий до получения редких сверхчистых веществ); оптические свойства тонких пленок (разнообразные лазерные технологии, распознавание и запись информации посредством лазеров, лазерная локация и системы наведения)
В-четвертых, живые клетки тоже в некоторых процессах сродни мыльным пузырям, что делает работу ценной с точки зрения биологии.
Итак, исследование мыльных пузырей оказалось интересным, красивым и полезным занятием.
II.ДОЛГАЯ ЖИЗНЬ МЫЛЬНОГО ПУЗЫРЯ. 2.1. Исторический очерк.
Детские, на первый взгляд, развлечения, не обходят стороной серьезных ученых. Чарльз Бойс сто лет тому назад опубликовал фундаментальный труд "Мыльные пузыри", который по сей день остается не только забавной книжкой для детей, но и настольным пособием для физиков-теоретиков и экспериментаторов. Одних патентов на выдувание мыльных пузырей к настоящему времени выдано многие тысячи. Некоторые из них имеют отнюдь не пустяшное значение.
При раскопках древних Помпеи археологи обнаружили необычные фрески с изображением юных помпейцев, выдувающих мыльные пузыри. Видимо, у них были свои секреты производства мыла, но мимо красочных воздушных пузырей пройти было невозможно.
2.2. Недолговечность мыльного пузыря?
Миф о недолговечности мыльного пузыря развеял англичанин Джеймс Дьюар, законсервировавший мыльный пузырь в герметичном сосуде с двойными стенками на срок более месяца. Забава оказалась полезной: позднее дьюар - сосуд, названный в честь изобретателя, — нашел применение для хранения и перевозки жидкого азота.
Преподавателю физики из штата Индиана удалось сохранить пузырь в стеклянной банке в течение 340 дней. Ученики превзошли учителя - их пузыри хранились под колпаком помногу лет, и это, похоже, не рекорд. Для обеспечения длительного хранения необходимо соблюсти условия тонкого равновесия мыльной пленки с окружающим и внутренним пространством, что оказалось далеко не простым делом. Поддержание формы мыльных пузырей требует основательных физических знаний и солидной экспериментальной подготовки.
2.3. Самый большой пузырь
Имя самого удачливого "надувателя" мыльных пузырей из Берна вошло в книгу рекордов Гиннеса: в 1985 году мастер публично выдул пузырь длиной 4 с половиной метра. Горячие головы вытворяют с мыльными пузырями невиданные трюки: десятками загоняют их один в другой, укладывают в длинные бисерные цепочки и складывают из них цветные узоры, заставляют танцевать на шерстяной или джинсовой ткани, а то и на невидимой подушке из углекислого газа. Профессиональные фокусники те вообще сделали мыльные пузыри предметом прибыльного ремесла, на потребу публике превращая воздушных акробатов в огромные стеклянные шары и прочие полезные и не очень предметы. Подсчитано, что из капли мыльной воды в 1 мм куб можно выдуть пузырь диаметром 20 см, а 1 мл раствора хватит на пузырь диаметром 6 м.
В патентной библиотеке можно найти патенты на устройства для выдувания гигантских мыльных пузырей. Патентуются как состав мыльных растворов, так и способ выдувания. "Мыльные пузыри гигантского размера можно выдуть с помощью небольшого карманного устройства (специальной трубки). Обычно диаметр пузырей составляет от 10 до 60 сантиметров, но можно выдувать и более крупные пузыри. Новизна изобретения состоит в конструкции устройства, которое использует принцип струйного насоса, поэтому при выдувании пузыря на один объем воздуха, выдыхаемого из легких, подсасывается от 3 до 10 объемов окружающего воздуха т.е., при одном и том же объеме выдоха пузырь получается в несколько раз больше, чем при выдувании через простую трубку."
2.4 Пузыри в биологии.
Процесс заморозки биологических мембран происходит также, как замораживание мыльного пузыря. Криоконсервация биологических субстанций широко используется в медицине. Изучать физические процессы, происходящие при заморозке мыльных пузырей, намного проще, чем на биологических объектах, содержащих избыточное число всевозможных факторов, неподдающихся строгому учету и физическому контролю. Таким образом, пузыри оказались полезны для изучения проблемы бессмертия.
Ученые из Северозападного университета в Чикаго обнаружили, что палочки и колбочки в сетчатке глаза упакованы по принципу уменьшения площади поверхности.
Именно так ведут себя мыльные пузыри, а значит законы элементарной физики применимы не только к неодушевленным шарикам из задачника, но и к живым организмам, начиная с клеток.
Ричард Картье, профессор биохимиии, молекулярной и клеточной биологии Северозападного университета, и соавтор его "теории мыльных пузырей" Такаши Хаяши не один год посвятили изучению сетчатки глаза. Исследуя клетки сетчатки плодовой мушки, они обнаружили, что, если поместить четыре клетки рядом, то они тут же объединятся в некую структуру с отверстием в центре. Точно так же ведут себя слипшиеся вместе четыре мыльных пузыря. Форма полученной структуры будет различаться в зависимости от числа клеток. Или пузырей. Но поведение и тех, и других будет аналогично.
"Они подходят друг к другу, как кусочки мозаики, - говорит профессор Картье. -Клетки живого организма упакованы на удивление совершенно. Наши опыты с мыльными пузырями и клетками сетчатки наглядно показали, что законы физики и математики применимы и ко всем живым существам, и что строение живой материи отвечает единому принципу".
2.5. Пузыри в нефтеперерабатывающей промышленности.
Для эффективной переработки нефти российские ученые предлагают использовать мицеллы - по сути, мыльные пузыри. Эти и другие исследования ПАВ поддерживаются российскими и международными грантами. Незаменимыми оказываются ПАВ и в химическом синтезе. В отличие от традиционной полимеризации в массе, эмульсионная полимеризация с образованием новых веществ осуществляется в мицеллах и существенно увеличивает скорость и выход синтеза. Именно такой способ начинает преобладать в производстве таких распространенных полимеров как поливинилацетат, полихлорпрен, полиметакрилат (органическое стекло), полихлорвинил, полиакриламид и многие другие.
Так что жизнь мыльного пузыря, несмотря на пословицу о быстротечности существования, обещает быть долгой и полезной.
III.Теория мыльных пузырей. Физические явления и их объяснение. 3.1. Монослой на поверхности воды. Адсорбция.
Оказывается, у достаточно сложных молекул имеются свои пристрастия. Например, одни органические молекулы "любят" контактировать с водой, а другие избегают такого контакта, "боятся" воды. Их и называют соответственно гидрофильными и гидрофобными молекулами.
Существуют, однако, еще и молекулы вроде русалок — одна их часть гидрофильная, а другая гидрофобная. Молекулы-русалки должны решить для себя проблему: быть им в воде или не быть (если мы пытаемся приготовить их водный раствор). Найденное решение оказывается поистине соломоновым: конечно же, они будут в воде, но только наполовину. Молекулы-русалки располагаются на поверхности воды так, что их гидрофильная головка (обладающая, как правило, разделенными зарядами - электрическим дипольным моментом) опущена в воду, а гидрофобный хвост (обычно это углеводородная цепочка) высовывается наружу в окружающую газообразную среду (рис. 1). Положение русалок несколько неудобное, зато оно удовлетворяет одному из основных принципов физики систем из многих частиц - принципу минимума свободной энергии.
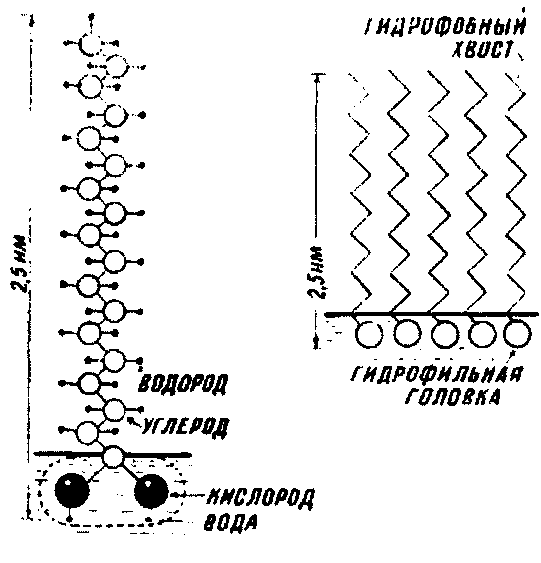
Рис. 1. При образовании мономолекулярного слоя на поверхности воды гидрофильные головки молекул опущены в воду, а гидрофобные хвосты торчат вертикально над водной поверхностью.
Молекулы моющих веществ - типичные "русалки". У них имеется длинная углеводородная цепь К, которая для случая мыла на основе стеариновой кислоты С17H35СООNa содержит 17 атомов углерода и короткую часть в виде реакционной солеобразующей (карбоксильной) группы.
Полярная часть молекулы обусловливает растворимость мыла в воде, неполярная (гидрофобная) — затрудняет, тормозит растворение и стремится вытеснить молекулу мыла из моющего раствора на поверхность. В связи с этим мыло в растворе концентрируется главным образом на поверхности моющего раствора. Соотношение длины неполярной и полярной частей в молекуле обусловливает различную растворимость моющего вещества в воде. С увеличением длины углеводородной цепи понижается растворимость, но повышается твердость моющего вещества. Например, мыло на основе стеариновой кислоты твердое, имеет низкую растворимость в воде комнатной температуры. При добавлении жирных кислот с меньшим количеством углеродных атомов улучшается растворимость мыла.
Здесь мы вплотную подходим к объяснению явления адсорбции. Оно заключается в том, что на поверхности жидкостей (и твердых тел) располагаются (адсорбируются ) те "чужие", "примесные", поверхностно-активные молекулы, которые способны понижать поверхностную энергию. Молекулы, адсорбируются на поверхности жидкости из объема вещества, если они там имеются в виде примеси или могут осесть из окружающей газовой среды. Учение об адсорбции — очень значительный раздел физической химии.
Существует огромный класс веществ - так называемые поверхностно-активные вещества, или сокращенно ПАВ, молекулы которых легко и охотно адсорбируются на поверхности жидкости. Такими веществами, в частности богаты мыла.
3.2. Внутреннее устройство мыльного пузыря
Благодаря поверхностной активности ПАВ понижают поверхностное натяжение воды. Прямыми измерениями было установлено, что адсорбция мыла на поверхности воды понижает ее поверхностное натяжение в два с половиной раза: от 7•10-2 до 3•10-2 Дж/м2
Стенка мыльного пузыря трехслойна: два внешних слоя мыла с глицерином разделены подвижной водной перегородкой, по которой они плавают. Глицерин добавляют для увеличения полярности длинных молекул растворителя. В результате в двойной мыльной пленке все водолюбивые хвосты молекулы мыла ориентированы внутрь пленки, водоотталкивающие - наружу. Собственно, по этой причине мыло и удаляет грязь — остатки органического и неорганического происхождения. Молекулы мыла со всех сторон облепляют частицы грязи гидрофобными хвостами внутрь, образуя так называемую мицеллу - растворимую в воде оболочку вокруг нерастворимого кусочка грязи. Избыток соли в растворе нарушает образование мицелл. Вот почему невозможно качественно помыться в морской воде, и пузыри из соленой воды не получаются.

Так схематически выглядит строение мыльной пленки,
укрепленной поверхностно-активными молекулами мыла
Итак, вследствии адсорбции мыла на поверхности воды образуется частокол удлиненных молекул. На поверхность они всплывают из объема. Что происходит с мыльной пленкой, ограничивающей пузырь, когда он раздувается? Ясно, что пленка растягивается. При этом частокол расположенных на его поверхности молекул мыла должен бы редеть, и могли бы появиться островки, свободные от адсорбированных молекул. Этого, однако, не происходит, так как скорость адсорбции велика и вслед за растяжением пленки на ее поверхность будут выходить молекулы мыла, достраивая частокол. Когда же все молекулы ПАВ выйдут из объема растягиваемой пленки на ее поверхность, дальнейшее растяжение пленки будет приводить к понижеению заселенности ее поверхности молекулами мыла.
3.3. Задача о предельном радиусе пузыря
Решим задачу о предельном радиусе пузыря R*, без нарушения сплошной поверхности. Если этот пузырь мы станем выдувать из капли мыльного раствора, радиус которой r, и в которой концентрация мыла равна c, то в нашем распоряжении окажется nс молекул мыла, которые мы можем расположить на поверхности пузыря предельного размера. Очевидно, если a - среднее межмолекулярное расстояние в жидкости, то
nс= (4/3πr3/a3)с
С другой стороны, для того чтобы и внешнюю, и внутреннюю поверхность мыльного пузыря покрыть однослойной пленкой молекул мыла, необходимо иметь
ns = 2•4π (R*/а)2 молекул. Тогда R * находится из условия ns = nс, т.е.
R*=(сr3/6а)1/2
Приравнивая объем начальной капли объему пленки пузыря :
4/3*πr3 = 4π R*2h*
можно найти толщину пленки предельного пузыря :
h=2а/с
Немного неожиданный результат: толщина пленки оказалась не зависящей ни от радиуса начальной капли, ни от радиуса предельного пузыря. Это вполне разумно и означает, что пленка предельного пузыря состоит из чистой, "обезмыленной" воды между двумя слоями молекул мыла. Чем больше было растворено мыла в воде (больше с), тем меньше будет "обезмыленной" воды (меньше h *)
Сделаем некоторые количественные оценки. Если r = 10-3 м, с ≈ 0,1, а≈5 ∙10 -10м, то оказывается, что R * ≈ 0,2 м, а h*≈ 10-8 м. А вот если r = 10~2 м, то R* ≈ 6 м. Такой пузырь очень сложно выдуть по "техническим причинам": он лопнет раньше, чем созреет.
3.4. Форма пузыря.
Тот пузырь, который свободно парит в воздухе, имеет сферическую форму. Впрочем, он сферический лишь в случае, если сила тяжести не вынуждает перемещаться жидкость в объеме пленки пузыря, и, следовательно, не приводит к тому, что пленка внизу оказывается толще, чем вверху, и форма пузыря искажается. Пленке свойственна противоположная тенденция. Она стремится сжаться, сократить свою поверхность, уменьшив при этом связанную с ней энергию. Как всегда в природе борющиеся тенденции находят разумное оптимальное решение. В случае нашей системы такое решение осуществляется, если пузырь примет форму сферы. Сфера при данной площади поверхности обеспечивает максимальный заключенный в ней объем. Форма сферы при данном объеме газа обеспечивает минимальную площадь поверхности. Удовлетворены обе конкурирующие тенденции.
Теперь о пузыре, висящем на соломинке. Как правило, его форма отличается от сферической по очевидной причине: в нижней части пузыря образуется скопление жидкости - капля, которая немного удлиняет пузырь, придавая ему грушевидную форму.
3.5. Взаимное притяжение соприкоснувшихся мыльных пузырей.
Мысленно приведем в соприкосновение два равновеликих мыльных пузыря и поразмышляем над тем, что же будет дальше. Если при соприкосновении на внешней поверхности каждого из пузырей адсорбционные слои окажутся нетронутыми, и если мы не приложим никаких усилий к тому, чтобы эти слои разрушить, соприкоснувшиеся пузыри должны сохранять свою индивидуальность, остаться безразличными друг к другу. Но представим себе, что в момент соприкосновения в месте контакта между пузырями образуется пятачок, по площади которого пузыри не разделены адсорбционными слоями. Ранее образовавшие их молекулы либо ушли в объем пленки, либо оттеснились на контур образовавшегося пятачка, радиус которого х. Появление такого пятачка означает, что на площади πx2 исчезнут две границы между пузырями, а это в свою очередь означает, что энергия пузырей уменьшилась на величину ΔWs = - 2πx2α. Обнаружившуюся возможность понижать энергию оба пузыря будут стремиться использовать, прижимаясь друг к другу и увеличивая при этом площадь контакта. Этот эффект можно назвать эффектом капиллярного притяжения.
Теперь о пленке, разделяющей два пузыря. Плоской эта пленка может быть лишь в том случае, если она разделяет два абсолютно равных пузыря, если она совпадает с плоскостью симметрии совокупности этих пузырей. Пусть теперь мембрана разделяет два пузыря, радиусы которых различны
R1 R2 В этом случае на мембрану действует давление
ΔP = P1 – P2 = 4 α(1/R1-1/R2)
Сила обусловленная давлением, направлена в сторону большего пузыря, в котором давление меньше.
Кажется странным: в пузырь нагнетается воздух, а мембрана все больше вдавливается в пузырь. Раздуваемый пузырь увеличивает свой радиус, а значит. Давление в нем не растет, а падает. Об этом и свидетельствует мембрана, прогибаясь навстречу потоку воздуха, который раздувает пузырь.
3.6. Элементарная теория разрушения пузыря.
После того, как пузырь достигнет предельного размера, его жизнеспособность с ростом радиуса будет быстро убывать, и "раздувшаяся смесь воды и мыла" лопнет.
Лопнуть пузырь может и по многим другим причинам : из-за тяжести водяной капли, образовавшейся в низу пузыря, его может порвать поток воздуха, его может проколоть пылинка, случайно осевшая на поверхность пузыря. Построить теорию разрушения пузыря, учитывающую все угрозы его жизни невозможно, т. к и угроз много, и так же много способов их осуществления. Но если задачу сузить и интересоваться лишь одной из возможных угроз, можно построить элементарную теорию разрушения пузыря. Допустим, что гибель пузыря наступила из-за того, что на его поверхность села пылинка и проколола пленку пузыря, образовав в нем пробоину. Значит, гибель пузыря окажется тем вероятнее, и, следовательно, длительность его жизни будет тем меньше, чем больше поверхность пузыря. Если оседание пылинки происходит случайно, то вероятность ее оседания на поверхность пузыря должна быть пропорциональной площади этой поверхности
S = 4π R2.
Сказанное можно записать так :
τ ~1/S~1/R2
Практика показывает, что приближенно этот закон выполняется.
Теперь попробуем описать случай, когда пузырь случайно проколот. Выясним условия, при которых пробоина, возникшая в том месте, где он проколот, будет действительно гибельной. Для этого нужно представить себе боковую поверхность пробоины. Она непроста и имеет форму кругового цилиндра, боковая поверхность которого изогнута так, как это показано на рисунке. Такую поверхность следует характеризовать двумя радиусами кривизны: r и R/2. Каждый из радиусов определяет лапласовские давления, из которых одно (Р→= 2α/h) способствует расширению, а другое (Р←= α /r)- сжатию пробоины.
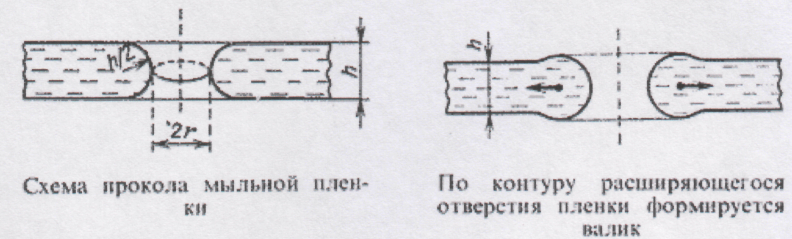
Ее судьба зависит от соотношения величин Р→ и Р← если
Р→ P←,- пробоина будет залечиваться, схлопываться. Для пузыря будут смертельными те пробоины, у которых r h/2. Если, например, h = 10-7 м, то появление пробоины радиусом r 5• 10-8 м означает гибель пузыря.
3.7. Оптика мыльного пузыря.
Горит, как хвост павлиний,
Каких цветов в нем нет!
Лиловый, красный, синий,
Зеленый, желтый цвет…*
Огнями на просторе
Играет легкий шар.
То в нем синеет море,
То в нем горит пожар.
С. Маршак
Физика XVIII века передала XIX веку по наследству противоречивые представления о природе света. К Ньютону восходили представления о "корпускулярном" свете - потоке гипотетических частиц - корпускул. Ньютон считал, что, попадая на сетчатку глаза, частицы возбуждают ощущение света: маленькие корпускулы создают впечатление фиолетового света, а корпускулы побольше - красного. Эти представления, объясняя закономерности распространения света, оставляли без всякого объяснения множество явлений, среди которых оказалась и интерференция света.
К Гримальди, Гуку и Гюйгенсу восходили представления о волновой природе света. Итальянский физик Франческо Гримальди, младший современник Ньютона, сравнивал распространение света с распространением волн на воде.
Мы вспомнили о рубеже между XVIII и XIX веками именно потому, что в это время жил один из величайших физиков Томас Юнг, который своими исследованиями обосновал волновые представления о свете, объяснив, в частности всевозможные проявления интерференции. Да и сам термин "интерференция" впервые ввел в науку именно Томас Юнг.
Этот человек добился успеха во многих областях деятельности (ботаника, музыка, живопись, металлургия, языковедение, филология, египтология, физика, математика, механика, цирковая гимнастика), но, пожалуй, наиболее значимые его достижения связаны с развитием представлений о волновой природе света и, в частности, о природе явления интерференции, о цветах тонких пленок. Французский физик Доменик Араго писал о Томасе Юнге: "Ценнейшее открытие доктора Юнга, которому суждено навеки обессмертить его имя, было ему внушено предметом, казалось бы, весьма ничтожным : теми самыми яркими и легкими пузырями мыльной пены, которые, едва вырвавшись из трубочки школьника, становятся игрушкой самых незаметных движений воздуха".
Вернемся к "оптике мыльного пузыря". Вначале вспомним, что нам уже известно об оптике из школьного курса физики. Нам известно, что распространение света - процесс волновой и что распространяющаяся монохроматическая волна имеет определенную длину волны λ0. Известно также, что световой луч отражается от поверхности раздела двух сред, а проходя сквозь эту границу, он преломляется. А еще известно, что так называемый "белый свет" является смесью разноцветных монохроматических лучей - от красного до фиолетового. Длина волны красного луча больше, чем фиолетового луча. И наконец, известно, что при переходе из пустоты в вещество пленки, длина волны λ0 изменяется, становится равной λв,. Величина n = λ0/λв называется показателем преломления.
Теперь направим под некоторым углом i на поверхность тонкой пленки толщиной h монохроматический свет, длина волны которого λ0. Произойдет вот что: луч света частично отразится от поверхности пленки, а частично, преломившись под углом r, войдет в ее объем. На нижней поверхности пленки произойдет то же самое: преломление и отражение. Отраженный луч вернется к верхней поверхности, отразится и преломится, и какая-то доля его выйдет из пленки, где встретится с одним из лучей падающего первичного пучка. Произойдет это в точке С. Точка эта, в основном, нас и интересует.
В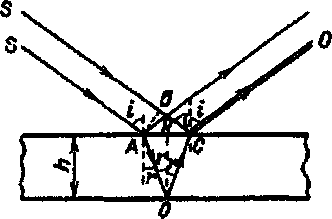
Схема к объяснению интенференции света в тонкой пленке
точке
С встречаются два луча, рожденные одним источником, но прошедшие разные пути. О таких лучах говорят "когерентные". Их отличительная особенность состоит в том, что разность фаз колебаний остается неизменной. Характер взаимодействия этих лучей в точке
С определяется разностью путей, пройденных ими до прихода в эту точку. Эта разность путей называется оптической разностью хода. Из очень несложного расчета, выполненного с помощью приведенного рисунка и определения
n = sin i /sin r следует, что
Δ = 2hn cos r
Мы подошли к самому существенному достижению Томаса Юнга. Он обратил внимание на то, что при выполнении условия Δ = 2kλ0 (k - целое число) могут иметь место два существенно различных эффекта : если k - четное число, волны усилят друг друга, а если нечетное - ослабят, точнее говоря, погасят друг друга.
Основываясь на формуле, определяющей Δ, мы можем очень многое понять в том, что называется "оптикой мыльного пузыря". В формуле при данном значении n воедино связаны длина волны света λ0, толщина пленки h и угол r, а следовательно, и угол падения пучка на пленку i. Предположим, что на поверхность пузыря, образованного пленкой постоянной толщины, падает пучок белого света и различные участки поверхности пузыря пучок встречает под различными углами. Это означает, что в условия, при которых отраженный луч усиливается, будут попадать лучи с различной длиной волны, и различные участки пузыря будут отсвечивать различными цветами радуги: "лиловый, красный, синий, зеленый, желтый цвет". Это может произойти и по другой причине : различные участки пленки пузыря со временем меняют свою толщину ( теперь уже меняется h ), и именно поэтому "то в нем синеет море, то в нем горит пожар". Если приглядеться к мыльному пузырю, можно отчетливо увидеть потоки жидкости, меняющие его окраску.
Ч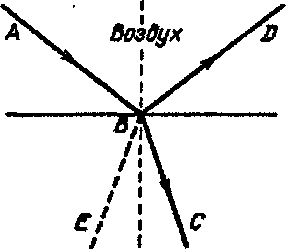 тобы закончить рассказ об оптике мыльного пузыря, обязательно надо сказать о черных полосах и пятнах в окраске пузыря. Они особенно отчетливо видны, когда пузырю осталось жить всего несколько мгновений.
тобы закончить рассказ об оптике мыльного пузыря, обязательно надо сказать о черных полосах и пятнах в окраске пузыря. Они особенно отчетливо видны, когда пузырю осталось жить всего несколько мгновений.
П
Схема, поясняющая появление “черных пятен” в расцветке тонкой пленки
опытаемся понять физическую причину появления черных пятен, вспомнив о том, что, обсуждая оптическую разность хода лучей в тонкой пленке
Δ, мы умолчали об одной детали во взаимодействии света с пленкой. Эта деталь не очень существенна, когда пленка толста
( h λ0), и не допускает пренебрежения собой, когда пленка тонка
(h λ0). Дело в том, что, как оказывается, отражение луча от границ воздух — пленка и пленка — воздух происходит так, что оптическая разность хода при этом скачком изменяется на половину длины волны. В соответствующем разделе теоретической оптики это обстоятельство доказывается математически строго. Известны, однако, совсем простые рассуждения английского физика Джорджа Стокса, отчетливо объясняющие это явление. Приведем его рассуждения. Если направление распространения луча, отраженного от границы воздух - пленка
(ВО), и луча, преломленного в ней
(ВС), обратить, они должны образовать луч
(ВА), равный по интенсивности и направленный противоположно первичному лучу
(АВ). Это утверждение справедливо, оно попросту отражает закон сохранения энергии. Обращенные лучи
СВ и
ОВ , вообще говоря , могли бы образовывать еще луч
(ВЕ). Он, однако, отсутствует, это -экспериментальный факт. Следовательно, в его создание лучи
СВ и
ОВ вносят вклады в виде лучей, которые равны по интенсивности, но смещены по отношению друг к другу на половину длины волны и поэтому гасят друг друга. Если к сказанному добавить, что один из этих лучей испытывал отражение от границы воздух - пленка, а другой от границы пленка - воздух, то станет ясно, что дополнительный скачок
Δ = λ0 /2 при отражении от границ между воздухом и пленкой происходит.
Возвратимся к черным пятнам и полосам. Если толщина пленки настолько мала, что оптическая разность хода, вычисленная без учета потери полуволны при отражении от границы воздух - пленка, оказывается малой по сравнению с длиной волны, то интерференция будет определяться только тем, что лучи смещены на половину длины волны, т. е. они будут гасить друг друга. А это означает, что возникает черная окраска пленки.
Всю логику рассказа о черных пятнах на мыльном пузыре можно бы обратить и утверждать следующее. Черная окраска очень тонких пленок - это факт. А, следовательно, при отражении двух лучей от границ воздух - пленка и пленка - воздух между ними должна возникать дополнительная оптическая разность хода, равная половине длины волны. Это путь не от логики к эксперименту, а от эксперимента к логике. Оба пути законны и дополняют друг друга.
Мы познакомились с идеями, которые в наши дни выглядят почти само собой разумеющимися, а в начале XIX века, во времена Томаса Юнга, были поразительным откровением. Ведь, подумать только: свет, слагаясь со светом, порождает тьму!
IV.Практическая часть. 4.1.Кристаллизация мыльного пузыря
Эта зима выдалась особенно морозной, что позволило мне изучить на практике кристаллизацию мыльного пузыря. Опишу несколько опытов.
4.1.1 Вращение.
Оказывается, пузырь, кристаллизующийся на соломинке, вращается. То есть, и некристаллизующийся тоже вращается, но когда пузырь вращается в процессе кристаллизации и останавливается, примерзая к трубке, это особенно наглядно.
Вращение пузыря можно объяснить так. В объеме пузыря из-за разности температур между различными участками его поверхности возникают внутренние воздушные потоки. Воздушная струя встречает поверхность пузыря под каким-то произвольным углом, а это означает, что должна возникнуть сила, поворачивающая пузырь. И направление потоков, и их расположение в объеме пузыря со временем меняются, а поэтому меняются и скорость, и направление его вращения.
4.1.2. Постепенность замерзания.
Впрочем, вращение — это не самое интересное наблюдение. Значительно интереснее следить за тем, как зарождаются и растут кристаллики в объеме пленки, образующей пузырь. Этот процесс напоминает развитие зимних узоров на запотевшем стекле. Собственно, это и есть тот же самый процесс : кристаллизация жидкой пленки. В начале процесса видны кристаллики - подобие снежинок. А затем отчетливо проявляются контуры растущих ледяных деревьев, переплетающихся ветвями. Ветви утолщаются, расширяются и закрывают собой все зазоры между ними. А в ином месте можно усмотреть контур лепестка розы. Фотографии прилагаются
4.1.3. Механические свойства.
Теперь рассмотрим механические свойства закристаллизовавшейся пленки пузыря.
Во-первых, пленка оказывается не хрупкой, какой, казалось бы, должна быть тонкая корочка льда. Если дать возможность мыльному закристаллизовавшемуся пузырю упасть на пол, он не разобьется, не превратится в звенящие осколки, как стеклянный шарик, каким украшают елку. На нем появятся вмятины, отдельные обломки закрутятся в трубочки. Пленка оказывается не хрупкой, она обнаруживает пластичность. Больше всего замерзший мыльный пузырь похож на целлофановый пакет.
Пластичность пленки оказывается следствием малости ее толщины. Это можно разъяснить следующим образом. По толщине тонкой поликристаллической пленки располагается, как правило, лишь одно зерно (монокристаллик). При действии на такую пленку деформирующих усилий каждое из составляющих ее зерен может почти беспрепятственно скользить относительно соседей, обусловливая, таким образом, ее пластичность. В нашем случае этот механизм может оказаться очень существенным, т. к вдоль границ между соседними зернами могут находиться тонкие жидкоподобные прослойки, обогащенные молекулами мыла, которые, как известно, понижают температуру кристаллизации воды. Такие прослойки облегчают взаимное скольжение зерен.
Кроме того, пленка, образующая закристаллизовавшийся пузырь, обнаруживает немалую прочность. Действительно, воздух, находящийся в объеме пузыря, градусов на 50 холоднее того, который мы вдохнули, раздувая пузырь. Это значит, что, когда воздух остывал, давление в объеме пузыря падало. А когда весь воздух остынет, пленка пузыря окажется под сжимающим давлением Рc=P0- Р1 = Р0Т1/Т0, где Р0=105 Па - давление в жидком пузыре, которое практически совпадает с атмосферным давлением, Т0=310К -начальная температура выдохнутого нами воздуха в жидком пузыре, Т1 =260 К -температура воздуха в пузыре после его кристаллизации, ΔТ = Т0- Т1. Таким образом, Рc =1,7•104 Па. Закристаллизовавшийся сферический пузырь должен выдерживать сжимающее давление, близкое 0,2 атмосферного, если пузырь остывал, будучи замкнутым, и его пленка была герметична.
4.1.4. Вмятина.
Вынесем баночку с мыльным раствором на сильный мороз (-250С) и выдуем пузырь. Сразу же в разных точках поверхности возникают мелкие кристаллики, которые быстро разрастаются и наконец сливаются. Как только пузырь полностью замерзнет, в его верхней части, вблизи конца трубки, образуется вмятина.
Воздух в пузыре и оболочка пузыря оказываются более охлажденными в нижней части, так как в вершине пузыря находится менее охлажденная трубка. Кристаллизация распространяется снизу вверх. Менее охлажденная и более тонкая (из-за отекания раствора) верхняя часть оболочки пузыря под действием атмосферного давления прогибается. Чем сильнее охлаждается воздух внутри пузыря, тем больше становится вмятина.
4.1.5. Тонкий пузырь.
Опустим конец трубки в мыльный раствор, а затем вынем. На нижнем конце трубки останется столбик раствора высотой около 4 мм. Приложим конец трубки к поверхности ладони. Столбик сильно уменьшится. Теперь выдуваем пузырь до появления радужной окраски. Пузырь получается с очень тонкими стенками. Такой пузырь ведет себя на морозе своеобразно: как только он замерзает, так сразу лопается. Так что получить замерзший пузырь с очень тонкими стенками никогда не удается.
Толщину стенки пузыря можно считать равной толщине мономолекулярного слоя. Кристаллизация начинается в отдельных точках поверхности пленки. Молекулы воды в этих точках должны сблизиться друг с другом и расположиться в определенном порядке. Перестройка в расположении молекул воды и сравнительно толстых пленках не приводит к нарушению связей между молекулами поды и мьша, тончайшие же пленки разрушаются.
4.1.6. Влияние глицерина.
Во все описанные в литературе составы для мыльных пузырей добавляют глицерин или сахарный раствор. В две баночки нальем поровну мыльный раствор. В одну добавим несколько капель чистого глицерина. Теперь из этих растворов один за другим выдуем два приблизительно равных пузыря. Замерзание пузыря с глицерином протекает немного иначе, чем пузыря из раствора шампуня: задерживается начало, и само замерзание идет медленнее. Замерзший пузырь из раствора шампуня сохраняется на морозе дольше, чем замерзший пузырь с глицерином.
Стенки замерзшего пузыря из раствора шампуня - монолитная кристаллическая структура. Межмолекулярные связи в любом месте совершенно одинаковы и прочны, в то время как в замерзшем пузыре из того же раствора с глицерином прочные связи между молекулами воды ослаблены. Кроме того, эти связи нарушаются тепловым движением молекул глицерина, поэтому кристаллическая решетка быстро сублимируется, а значит, быстрее разрушается.
4.1.7. Снежинка как центр кристаллизации.
На слабом морозе (-15ОС) выдуем пузырь. Дождемся, пока он лопнет. Повторим опыт с тем, чтобы убедиться, что пузыри не замерзают, сколько бы их ни выдерживали на морозе. Теперь приготовим снежинку. Выдуем пузырь и тут же сбросим на него сверху снежинку. Она мгновенно соскользнет вниз на дно пузыря. На том месте, где остановилась снежинка, начнется кристаллизация пленки. Наконец, весь пузырь замерзнет.
Пузыри на слабом морозе охлаждаются медленно и при этом переохлаждаются. Снежинка является центром кристаллизации. [8],[3]
V.Заключение.
Таким образом, на примере мыльного пузыря мы рассмотрели и обосновали ряд физических явлений, а именно:
абсорбция жидкости на границе жидкость-газ;
поверхностное натяжение;
уравнение Менделеева-Клайперона в действии:
поведение переохлажденной жидкости;
интерференция света в тонких пленках.
VI.Литература
Блинов Л. Молекулы-русалки “Наука и жизнь”, №4,1989
"Домашний монгольфьер" "Наука и жизнь № 6,2001 г.
Гегузин Я.Е. Пузыри - М.: Наука, 1985.
Гигантские мыльные пузыри. УСТРОЙСТВО ДЛЯ ВЫДУВАНИЯ МЫЛЬНЫХ ПУЗЫРЕЙ патент РФ № 2139119
“Известия науки”, портал http://www.inauka.ru ,редакция газеты "Известия", 2002
Перельман Я. “Занимательная физика”, Москва, 1967г.
Перышкин А.В. "Физика. 8 кл."
Пузыри на морозе. “Наука и жизнь”, №2,1982.
Шварц А., Перри Дж., Берн Д ж., Поверхностноактивные вещества и моющие средства, М., 1960
Лущекина О.Б., школа № 307, г. Москва “Шоу мыльных пузырей, или куда может завести работа над проектом”, газета “Физика”, №22 2004г.
13











 тобы закончить рассказ об оптике мыльного пузыря, обязательно надо сказать о черных полосах и пятнах в окраске пузыря. Они особенно отчетливо видны, когда пузырю осталось жить всего несколько мгновений.
тобы закончить рассказ об оптике мыльного пузыря, обязательно надо сказать о черных полосах и пятнах в окраске пузыря. Они особенно отчетливо видны, когда пузырю осталось жить всего несколько мгновений.

















