5.Тема: Дискреттик математиканын элементтери
1. Комбинаторика
2.Орундаштыруу
3.Орун алмаштыруулар
4.Топтоштуруулар
1. Комбинаторика
Комбинаторика - чектүү көптүктөрдүн, б.а. белгилүү бир сандагы нерселердин, мисалы: сандардын, тамгалардын, геометриялык фигуралардын түрлүүчө комбинацияларынын үстүнөн жүргүзүлүүчү кээ бир амалдарды үйрөтүүчү математиканын бир бөлүмү.
Демек, турмушта, практикада берилген чектүү сандагы элементтердин жана обьектилердин арасынан керектүү бир нечесин тандап алуу, же аларды түрдүү жол менен жайгаштыруу жөнүндөгү маселелер көп кездешет.
Ага мисалдарды карап көрөлү.
1-мисал. Театрдын кассасына келген 100 киши канча түрдүү жол менен кезек күтүүлөрү мүмкүн?
2-мисал. Шахмат боюнча турнирде ойногон 18 оюнчулар канча түрдүү жол менен биринчи үч сыйлыкты бөлүшө алышат?
3-мисал. Автомобилдин номерлери 2 тамгадан жана 4 цифрадан турса, мүмкүн болгон канча машинага номер бурүүгө болот?
Мына ушул сыяктуу маселелерди чыгаруунун жалпы эрежеси – берилген чектүү сандагы элементтердин же алардын ар түрдүү мүмкүн болгон жайгаштырууларынын санын табуу болуп эсептелет. Мындай маселелер комбинатаңориканын маселелери деп аталат.
Комбинаториканын негизги эрежелери: 1-эреже. Эгерде удаалаш тандалуучу элементтердин: биринчисин – n1 түрдүү жол менен, экичнсин – n2 түрдүү жол менен, үчүнчүсүн- n3 түрдүү жол менен, ушул сыяктуу эле k- чысын nk түрдүү жол менен тандоого мүмкүн болсо, анда k элементти бирге n1 ‘ n2’…nkтүрдүү жол менен тандап алууга мүмкүн. Бул эреже көбөйтүүнүн эрежеси деп аталат.
2-эреже. Эгерде n элементүү көптүк берилсе, анда анын k элементтүү майда көптүкчөлөрү n элементтен k алынып түзүлгөн топтоштуруулар деп аталат.
1-теорема. n элементтүү көптүктүн k элементтүү көпчтүкчөлөрүнүн саны, б.а. n элементтен k элементтер боюнча түзүлгөн баардык топтоштуруулардын саны (3.1.) формуласы аркылуу аныкталат.
n элементтүү көптүктүн k-1 элементтүү топтоштурууларынын саны 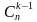 менен белгилейли. Анда алардын ар бирине, ага кирбеген
менен белгилейли. Анда алардын ар бирине, ага кирбеген 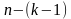 элементтен бирден кошуу менен k –элементүү көптүкчөлөрдү түзөлү. Алардын саны
элементтен бирден кошуу менен k –элементүү көптүкчөлөрдү түзөлү. Алардын саны 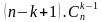 болот. Бирок, бул учурда ар бир k –элементүү көптүкчө k жолу кайталангандыктан барабардыгы орун алат, б.а. болот.
болот. Бирок, бул учурда ар бир k –элементүү көптүкчө k жолу кайталангандыктан барабардыгы орун алат, б.а. болот.
Бул рекуренттүү формуладан 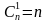 экендигин эске алсак, анда: изделүүчү формула келип чыгат.
экендигин эске алсак, анда: изделүүчү формула келип чыгат.
1-маселе. Студент китепканадагы беш кызыктуу китептин үчөөсүн канча түрдүү жол менен тандап алышы мүмкүн?
Болгондуктан, студент 10 түрдүү жол менен 5китептин үчөөсүн тандашы мүмкүн.
2-маселе. Группада 10 эркек бала жана 15кыз бар. Конференцияга 2эркек бала 2кыз болгондой кылып 4делегатты канча түрдү жол менен шайлоого мүмкүн?
2студент эркек бала конференцияга делегат боло алат, демек аларды 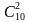 түрдүү жол менен тандоого мүмкүн. Ал эми 2 студент кызды болсо
түрдүү жол менен тандоого мүмкүн. Ал эми 2 студент кызды болсо 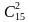 жолу менен тандоого болот. Анда комбинаториканын негизги эрежеси боюнча 4делегатты 25студенттин арасынан берилген шартты канааттандыра тургандай кылып
жолу менен тандоого болот. Анда комбинаториканын негизги эрежеси боюнча 4делегатты 25студенттин арасынан берилген шартты канааттандыра тургандай кылып 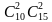 түрдүү жол менен тандоого мүмкүн.
түрдүү жол менен тандоого мүмкүн.
3-эреже. Көптүктөгү элементтердин ээлеген орду мааниге э болсо, анда ар бир элементти 1ден 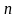 ге чейинки натуралдык сандар менен номерлөөгө болот. Мындай көптүк тартиптештирилген көптүк деп аталат.
ге чейинки натуралдык сандар менен номерлөөгө болот. Мындай көптүк тартиптештирилген көптүк деп аталат.
2-теорема. 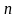 элементтүү көптүктүн тартиптештирилген көптүктөрүнүн саны, б.а.
элементтүү көптүктүн тартиптештирилген көптүктөрүнүн саны, б.а. 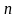 элементтен түзүлгөн орун алмаштыруулардын саны
элементтен түзүлгөн орун алмаштыруулардын саны 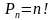 аркылуу аныкталат.
аркылуу аныкталат.
Бултеореманы негизги эрежени колдонуп далилдесе болот. Ал үчүн 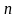 орундуу клетканы алалы.
орундуу клетканы алалы.
1-клеткага 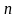 элементтин каалаган бирөөнү, 2-клеткага
элементтин каалаган бирөөнү, 2-клеткага 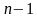 - элементтин каалаганын жайгаштырууга болот, ж.б.д. у.с.
- элементтин каалаганын жайгаштырууга болот, ж.б.д. у.с. 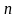 - клеткага акырында калган 1 гана элементти жайгаштыруу мүмкүн, анда комбинаториканын негизги эрежеси боюнча
- клеткага акырында калган 1 гана элементти жайгаштыруу мүмкүн, анда комбинаториканын негизги эрежеси боюнча 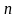 -элементтен түрдүүчө тартиптештирүүнүн мүмкүн болгон бардык саны
-элементтен түрдүүчө тартиптештирүүнүн мүмкүн болгон бардык саны 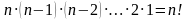 болот. Ошентип
болот. Ошентип 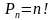 . Теорема далиденди.
. Теорема далиденди.
4-эреже. 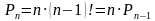 рекуренттик барабардыктан
рекуренттик барабардыктан 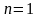 болгондо
болгондо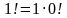 Болот. Ошондуктан
Болот. Ошондуктан 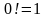 деп алабыз.
деп алабыз.
3-маселе. 4китепти канча түрдүү жол менен китеп текчеге жайгаштыруу мүмкүн?
Бул маселе 4 элементтүү көптүктүн тартиптештирилген көптүктөрүнүн санын, б.а. 4 элементтен түзүлгөн орун алмаштыруулардын санын аныктоого арналган.
Демек, 4 китепти текчеге 24жол менен жайгаштырууга болот.
5-эреже. 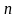 элементтүү көптүктүн k элементтүү тартиптештирилген көптүкчөлөрү
элементтүү көптүктүн k элементтүү тартиптештирилген көптүкчөлөрү 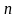 элементтен k дан алынып түзүлгөн орундаштыруулар деп аталышат.
элементтен k дан алынып түзүлгөн орундаштыруулар деп аталышат.
3-теорема. 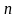 элементтүү көптүктүн k элементтүү тартиптештирилген көптүкчөлөрүнүн саны, б.а.
элементтүү көптүктүн k элементтүү тартиптештирилген көптүкчөлөрүнүн саны, б.а. 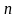 элементтеги k элементтер боюнча түзүлгөн орундаштыруулардын саны төмөндөгүдөй аныкталат. (3.2)
элементтеги k элементтер боюнча түзүлгөн орундаштыруулардын саны төмөндөгүдөй аныкталат. (3.2)
Бул теореманы далилдө үчүн 1-теореманы жана 2-теореманы пайдалануу керек. Чындыгында 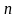 элементтүү көптүктүн k элементтүү көптүкчөлөрүнүн саны 1-теорема боюнча
элементтүү көптүктүн k элементтүү көптүкчөлөрүнүн саны 1-теорема боюнча
Ал эми ар бир k элементтүү боюнча 2-теорема боюнча  жолу ар түрдүүчө тартиптештирүүгө болот. Анда
жолу ар түрдүүчө тартиптештирүүгө болот. Анда 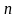 элементтүү көптүктүн k элементтүү тартиптештирилген көптүкчөлөрүнүн саны га барабар. Ошентип
элементтүү көптүктүн k элементтүү тартиптештирилген көптүкчөлөрүнүн саны га барабар. Ошентип 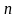 элементтен k элементтер боюнча түзүлгөн орундаштыруулардын саны боюнча аныкталат.
элементтен k элементтер боюнча түзүлгөн орундаштыруулардын саны боюнча аныкталат.
4-маселе. Аудиториядагы 20 орунга 4студент канча түрдүү жол менен жайланышып отурууга мүмкүн?
Бул маселе 20элементтен 4төн алынган орундаштыруулардын санын эсептөөгө алып келет болгондуктан, аудиториядагы 20 орунга 4студент 110160 түрдүү жол менен жайгаштыруу мүмкүн.
5-маселе. Автомобилдин номерлери 3тамгадан 4цифрадан турса, канча автомобилге номер берүүгө болот (эгерде 3тамгасы кайталанбаса)?
Орус алфавитинде бардыгы 32 тамга бар. Эгерде 3 тамгасы кайталанбаса, анда тамгаларга карата сериялардын саны 32элементтен 3төн алынып түзүлгөн орундаштыруулардын санына барабар, б.а. га барабар.
Ар бир серияда 9999номер болгондуктан, бул учурда 29760х297470240 автомобилди номерлөөгө болот.
Толук ыктымалдыктын формуласы
1-эреже. Биргелешпеген окуялардын толук группасын түзгөн  окуялардын системасын карайлы. Айталы, В окуясы алардын каалаган бирөө менен биргелешип келип чыга тургандай окуя болсун. Анда
окуялардын системасын карайлы. Айталы, В окуясы алардын каалаган бирөө менен биргелешип келип чыга тургандай окуя болсун. Анда  окуяларынын биргелешпеген болушунан төмөнкү барабардыкты алууга болот.
окуяларынын биргелешпеген болушунан төмөнкү барабардыкты алууга болот.
(5.1)
Андан биргелешпеген чектүү сандагы окуялардын суммасынын ыктымалдыгын табуунун формуласын (5.2) пайдаланып,
(5.3)
алабыз. Жогорку барбардыкта каалаган эки окуянын көбөйтүндүсүнүн ыктымалдыгынын (5.4) формуласын колдонсок, , (5.5)
болот жана ал толук ыктымалдыктын формуласы деп аталат.
 - гипотезалардын аткарылышынын ыктымалдыктары белгилүү болсо жана гипотезалар аткарылды дегенден кийинки В окуясынын шарттуу ыктымалдыктары белгилүү болсо, анда В окуясынын ыктымалдыгы (5.5) формуласы боюнча эсептелет. Мында дайыма
- гипотезалардын аткарылышынын ыктымалдыктары белгилүү болсо жана гипотезалар аткарылды дегенден кийинки В окуясынын шарттуу ыктымалдыктары белгилүү болсо, анда В окуясынын ыктымалдыгы (5.5) формуласы боюнча эсептелет. Мында дайыма  - окуялары толук группаны түзүшө тургандыгын эске алуу керек.
- окуялары толук группаны түзүшө тургандыгын эске алуу керек.
Байестин формуласы
1-эреже. Биргелешпеген окуялардын толук группасын түзгөн  окуяларынын системасын карайлы. Алардын кандайдыр биринин аткарылышы менен В окуясы келип чыксын
окуяларынын системасын карайлы. Алардын кандайдыр биринин аткарылышы менен В окуясы келип чыксын  окуяларынын кайсынысы аткарылганда В окуясы келип чыгары белгисиз болгондуктан, алар гипотезалар деп аталат). Анда гипотезалардын ыктымалдыгы өзгөрөбү, эгер өзгөрсө кайсы формула боюнча аларды баалоого болот? -деген суроолор келип чыгат б.а.
окуяларынын кайсынысы аткарылганда В окуясы келип чыгары белгисиз болгондуктан, алар гипотезалар деп аталат). Анда гипотезалардын ыктымалдыгы өзгөрөбү, эгер өзгөрсө кайсы формула боюнча аларды баалоого болот? -деген суроолор келип чыгат б.а.  көрүнүшүндөгү шарттуу ыктымалдыктарды аныктоо керек болот. Ал үчүн өз ара көз каранды эки окуянын көбөйтүндүсүнүн ыктымалдыгын табуу формуласын пайдаланабыз.
көрүнүшүндөгү шарттуу ыктымалдыктарды аныктоо керек болот. Ал үчүн өз ара көз каранды эки окуянын көбөйтүндүсүнүн ыктымалдыгын табуу формуласын пайдаланабыз.  (6.1)
(6.1)
Мындан (6.2)
алабыз. Ал эми  үчүн толук ыктымалдыктын формуласын пайдалансак, анда:
үчүн толук ыктымалдыктын формуласын пайдалансак, анда:  (6.3) формуласы келип чыгат.
(6.3) формуласы келип чыгат.
Бул формуланы 1764-жылы англиялык математик Байес (же Бейес) ойлоп тапкандыктан, Байестин формуласы деп аталат. Ал формула сыноонун натыйжасында В окуясы келип чыккандан кийин,  гипотезаларынын ыктымалдыктарын кайра балоого мүмкүндүк берет.
гипотезаларынын ыктымалдыктарын кайра балоого мүмкүндүк берет.
1-маселе. Факультеттеги 800 студенттин 72 си отличник ал эми 320 студент жок дегеден бир сабактан “эң жакшы” деген рейтингге ээ. Факультетте учураган биринчи студенттин жок дегенде бир сабакты бешке окушунун ыктымалдыгын тапкыла.
Окуялар: А- биринчи жолуккан студент отличник, В биринчи жолуккан студент жок дегенде бир сабактан “5” ке окуйт.  , анда A жана В окуялары биргелешпеген окуялар болушат. Ошол себептүү: .
, анда A жана В окуялары биргелешпеген окуялар болушат. Ошол себептүү: .
2-маселе. “Ак Жибек” мамлекеттик акционердик коомунун продукциясынын 95%ти стандартка туура келет жана анын ичинен 86% I-сортто болсо, бул ишкананын каалаган эле бир продукциясынын 1-сортто болушунун ыктымалдыгын тапкыла.
А –каалагандай алынган эле бир продукция стандартка туура келет деген окуя. В- стандартка туура келген продукция 1-сортто деген окуя. Анда шарт боюнча болот. Демек каалаган бир продукциянын 1-сортто болушунун ыктымалдуулугу
Бернуллинин формуласы
Каралуучу n сыноолордун ар биринде А окуясы р ыктымалдыгы менен т жолу келип чыгышы мүмкүн болсун. Ал ыктымалдуулук ар бир сыноо үчүн турактуу экендиги аныкталсын жана А окуясынын канча жолу келип чыккандыгынан көз каранды болбосун. Мындай сыноолордун удаалашытыгы көз каранды эмес сыноолор деп аталат.
Айталы, n көз каранды эмес сыноолордун ар биринде А окуясы ыктымалдык менен келип чыксын. Анда n сыноо учурунда
 А окуясынын т жолу келип чыгышынын ыктымалдуулугун табуу керек болсун. Ушундай ыктымалдуулукту эсептөөгө келтирилүүчү жалпы формуланы табабыз. Ал үчүн n жолку бирдей көз каранды эмес сыноо кезинде
А окуясынын т жолу келип чыгышынын ыктымалдуулугун табуу керек болсун. Ушундай ыктымалдуулукту эсептөөгө келтирилүүчү жалпы формуланы табабыз. Ал үчүн n жолку бирдей көз каранды эмес сыноо кезинде
А окуясы туп-туура т жолу келип чыксын дейли. Ар бир сыноодо А окуясынын келип чыгышынын ыктымалдыгы болсун. А окуясы n жолку чыноодо т жолу келип чыкса, анда  жолу ага карама-каршы окуя болгон
жолу ага карама-каршы окуя болгон  окуясы келип чыгаары түшүнүктүү. Ошондуктан, ыктымалдыктарды көбөйтүүнүн эрежеси боюнча
окуясы келип чыгаары түшүнүктүү. Ошондуктан, ыктымалдыктарды көбөйтүүнүн эрежеси боюнча

окуясынын ыктымалдыгы  га барабар. Бирок, n жолку сыноо кезинде А олкуясынын т жолу келип чыгышы n элементтен т элемент боюнча топтоштурууга барабар болот, б.а.
га барабар. Бирок, n жолку сыноо кезинде А олкуясынын т жолу келип чыгышы n элементтен т элемент боюнча топтоштурууга барабар болот, б.а.  га барабар. Кандай тартипте келип чыкса дагы, А окуясы т жолу, ал эми
га барабар. Кандай тартипте келип чыкса дагы, А окуясы т жолу, ал эми  окуясы
окуясы  жолу келип чыккандыктан, мындай ар бир n сыноолордун натыйжасын ыктымалдыгы
жолу келип чыккандыктан, мындай ар бир n сыноолордун натыйжасын ыктымалдыгы  болот. Ошондуктан ыктымалдыктарды кошуу эрежеси боюнча А окуясынын m жолу келип чыгышынын ыктымалдыгы ге барабар болот. Ал ыктымалдыкты
болот. Ошондуктан ыктымалдыктарды кошуу эрежеси боюнча А окуясынын m жолу келип чыгышынын ыктымалдыгы ге барабар болот. Ал ыктымалдыкты  менен белгилөө кабыл алынган. Демек, , (1.1)
менен белгилөө кабыл алынган. Демек, , (1.1)
Бул формуланы Бернуллинин формуласы дейбиз. Мында, n сыноонун саны, т- окуянын кайталанышынын саны, р-бир жолку сыноодо А окуясынын келип чыгышынын,  бир жолку сыноодо
бир жолку сыноодо  окуясынын келип чыгышынын ыктымалдыгы. Ал эми элементтен т ден алып түзүлгөн топтоштуруунун саны.
окуясынын келип чыгышынын ыктымалдыгы. Ал эми элементтен т ден алып түзүлгөн топтоштуруунун саны.
1-маселе. Завод 0,9 ыктымалдык менен сапаттуу тектиктерди даярдайт. Ал даярдаган 5 тетиктин ичинен үчөөнүн сапаттуу болушунун ыктымалдыгын тапкыла.
Бернуллинин формуласы боюнча.
болот.
2-маселе. Бир үй-бүлөнүн 10 бласаы бар. Эркек жана кыз баланын төрөлүшүнүн ыктымалдыгы 0б5 болсо, алардын бешөө эркек бала, ал эми бешөө кыз бала экендигинин ыктымалдыгын тапкыла.
болгондуктан
Демек, 10 баласы бар үй-бүлөнүн 10 баласы бар үй-бүлөнүн беши кыз, беши эркек бала болушунун ыктымалдыгы 0,246 болот.
3-маселе. Улан менен Куттубек 6партия шахмат ойноого убадалашты. Ар бир партияда Уландын утулушунун ыктымалдыгы  ге барабар. Куттубектин утулушунун ыктымалдыгы болсо
ге барабар. Куттубектин утулушунун ыктымалдыгы болсо  ге барабар. Бир партияда тең чыгуу эске алынбаса, Уландын утулушунун жана оюндун тең чыгышынын ыктымалдыктарын тапкыла.
ге барабар. Бир партияда тең чыгуу эске алынбаса, Уландын утулушунун жана оюндун тең чыгышынын ыктымалдыктарын тапкыла.
1)

2) Тең чыгыш үчүн 
4 элементтен турган 3 элементтүү орундаштыруу 24 кө барабар:
.
1-мисал. Эсептегиле:  ,
,  ,
,  .
.
Чыгаруу:
,
,
.
2-мисал. Класстагы 20 орунга 4 окуучуну канча түрдүү жол менен жайгаштырууга болот?
Чыгаруу: .
Демек, класстагы 20 орунга 4 окуучуну 116280 түрдүү жол менен жайгаштырууга болот.
3-мисал. Автомобилдин номери 4 цифра жана 2 тамгадан турса канча түрдүү номер чыгарууга болот?
Чыгаруу: Кыргызстанда “Z 18 19 Z”, “Z 10 95 В” ж.б.с.у номерлерди мамлекет чыгарат. Демек тамгалары кайталанышы мүмкүн экен жана англис тилинин 26 тамгасы пайдаланылат деп эсептейли. Анда тамгаларга карата 26х26=676 серия бар, ал эми ар бир серияда 9999 номер чыгат. Анда 676х9999=6759324 номер чыгарууга болот.
Орун алмаштыруулар
m элементтен түзүлгөн  элементтүү орундаштыруу m элементтүү орун алмаштыруу деп аталат. б.а.
элементтүү орундаштыруу m элементтүү орун алмаштыруу деп аталат. б.а.
Көптүктүн бардык элементтерин өзүндө кармаган жана бири-биринен элементтеринин жайгашкан ирети менен гана айырмаланган биригүү – орун алмаштыруу деп аталат.
Орун алмаштыруу орундаштыруунун айрым учуру болот.
m элементтен түзүлгөн көптүктүн бардык m эленеттүү орун алмаштыруулары да m элементтен турат, ошондуктан алар бири биринен элементтеринин тартиби менен гана айырмаланат.
m элементтүү орун алмаштыруулардын саны  формуласы аркылуу аныкталат.
формуласы аркылуу аныкталат.
Орун алмаштырууларды белгилөө үчүн франсуз тилиндеги Permutation (орун алмаштыруу) деген сөздүн биринчи тамгасы болгон Р тамгасы кабыл алынаган.
1-мисал. Эсептегиле  .
.
Чыгаруу: ,
.
2-мисал. Класста дежур болуу үчүн бир жумага 6 окуучу бөлүнгөн. Канча түрдүү жол менен кезекти уюштурууга болот?
Чыгаруу: .
Топтоштуруулар
m элементтенттүү көптүк берилсин.  элементтүү көптүктүн ар бир
элементтүү көптүктүн ар бир  элементттүү бөлүкчө көптүктөрү
элементттүү бөлүкчө көптүктөрү  элементтен
элементтен  элементтүү топтоштуруу деп аталат.б.а.
элементтүү топтоштуруу деп аталат.б.а.
m элементтин n элементинен турган жана бири-биринен жок дегенде бир элементи менен айырмаланган биригүү - m элементтен n боюнча топтоштуруу деп аталат.
Бул учурда m элементтүү көптүктүн n элементтүү бөлүкчө көптүктөрү бири биринен элементеринин курамы менен айырмаланат. Эгерде бөлүкчө көптүктөрүнүн арасында элементтеринин тартиби менен гана айырмаланган көптүктөр болсо, анда аларды окшош деп эсептейбиз.m элементтүү көптүктүн бардык n элементттүү топтош-турууларынын саны формуласы менен аныкталат.
Топтоштурууларды белгилөө үчүн франсуз тилиндеги Combinasion (топтоштуруу) деген сөзүнүн биринчи тамгасы болгон С кабыл алынган.
1-мисал. Жогорудагы мисалда көрсөтүлгөндөй 4 элементтен турган  көптүгүнүн 3 элементтүү 4 бөлүкчө көптүгү бар:
көптүгүнүн 3 элементтүү 4 бөлүкчө көптүгү бар:  .
.
2-мисал. Эсептегиле:  .
.
Чыгаруу: .
.
Орундаштыруулардын, орун алмаштыруулардын жана топтоштуруулардын санын эсептөө формулаларынын төмөнкүдөй касиеттери бар:
 .
. 
 .
. 
3.
 .
.
 - касиеттин маанисин төмөндөгүчө түшүндүрүүгө болот.:
- касиеттин маанисин төмөндөгүчө түшүндүрүүгө болот.:  топтоштуруусу m элементтүү көптүктүн n элементтүү бөлүкчө көптүктөрүнүн санын аныктагандыктан, m элементтүү көптүктүн бардык бөлүкчө көптүктөрүнүн саны суммасына
топтоштуруусу m элементтүү көптүктүн n элементтүү бөлүкчө көптүктөрүнүн санын аныктагандыктан, m элементтүү көптүктүн бардык бөлүкчө көптүктөрүнүн саны суммасына  барабар болот. Демек,
барабар болот. Демек,  - касиет боюнча m элементтүү көптүктүн бардык бөлүкчө көптүктөрүнүн саны
- касиет боюнча m элементтүү көптүктүн бардык бөлүкчө көптүктөрүнүн саны  болот.
болот.







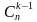 менен белгилейли. Анда алардын ар бирине, ага кирбеген
менен белгилейли. Анда алардын ар бирине, ага кирбеген 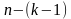 элементтен бирден кошуу менен k –элементүү көптүкчөлөрдү түзөлү. Алардын саны
элементтен бирден кошуу менен k –элементүү көптүкчөлөрдү түзөлү. Алардын саны 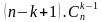 болот. Бирок, бул учурда ар бир k –элементүү көптүкчө k жолу кайталангандыктан барабардыгы орун алат, б.а. болот.
болот. Бирок, бул учурда ар бир k –элементүү көптүкчө k жолу кайталангандыктан барабардыгы орун алат, б.а. болот.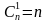 экендигин эске алсак, анда: изделүүчү формула келип чыгат.
экендигин эске алсак, анда: изделүүчү формула келип чыгат.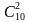 түрдүү жол менен тандоого мүмкүн. Ал эми 2 студент кызды болсо
түрдүү жол менен тандоого мүмкүн. Ал эми 2 студент кызды болсо 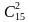 жолу менен тандоого болот. Анда комбинаториканын негизги эрежеси боюнча 4делегатты 25студенттин арасынан берилген шартты канааттандыра тургандай кылып
жолу менен тандоого болот. Анда комбинаториканын негизги эрежеси боюнча 4делегатты 25студенттин арасынан берилген шартты канааттандыра тургандай кылып 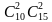 түрдүү жол менен тандоого мүмкүн.
түрдүү жол менен тандоого мүмкүн.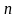 ге чейинки натуралдык сандар менен номерлөөгө болот. Мындай көптүк тартиптештирилген көптүк деп аталат.
ге чейинки натуралдык сандар менен номерлөөгө болот. Мындай көптүк тартиптештирилген көптүк деп аталат.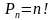 аркылуу аныкталат.
аркылуу аныкталат.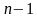 - элементтин каалаганын жайгаштырууга болот, ж.б.д. у.с.
- элементтин каалаганын жайгаштырууга болот, ж.б.д. у.с. 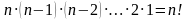 болот. Ошентип
болот. Ошентип 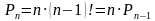 рекуренттик барабардыктан
рекуренттик барабардыктан 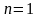 болгондо
болгондо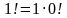 Болот. Ошондуктан
Болот. Ошондуктан 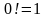 деп алабыз.
деп алабыз.


















