Делимость многочленов (презентация)

Департамент образования мэрии города Новосибирска

Дворец творчества детей и учащейся молодёжи «Юниор»

Деление многочленов: свойства, способы и области применения

Автор:

Сивова Маргарита, 8 класс, МБОУ «Гимназия №13 имени Э.А.Быкова»

Центральный округ г.Новосибирска

2020г

Актуальность:

для успешной сдачи ОГЭ и ЕГЭ по математики важно умение делить многочлены – это может заметно упростить решение задачи, но данная тема в школьной программе отсутствует. Поэтому изучение теории делимости многочленов уже в текущих классах может помочь мне при решении алгебраических задач.

Задание №21 ОГЭ

Сократите дробь                                           

Решение :

Разложим числитель на множители, используя метод группировки:

Приведём другое решение.

Последовательно разделим многочлен на одночлены в столбик:

Проблема: В школьной программе отсутствует тема деления многочленов, однако это знание может помочь при решении математических уравнений и задач.

Способы решения проблемы:

• получение информации из различных источников (интернет, математические справочники и учебники, научные работы);
• Создание собственного справочника на выбранную тему.

Цель: Изучение способов и свойств деления многочленов.

Задачи проекта:

1. Изучить основные понятия, теоремы и алгоритмы теории делимости;

2. Подобрать задачи и алгоритмы их решения для учащихся 7-8 классов на применение теории делимости многочленов; 3. Создать буклет-справочник для ежедневного использования.

Методы: Анализ научной литературы.

Продукт: Математический справочник на основе полученных знаний.

Ресурсы: Полученная информация, бумага, деньги.

План проекта:

• К 1 марта 2020 года изучить основные понятия, теоремы и алгоритмы теории делимости;
• К 20 марта 2020 года подобрать задачи для самостоятельного решения учащимся 7-8 классов;
• К 25 мая 2020 года создать буклет-справочник для ежедневного использования.

Планируемый результат:

• Справочник-буклет должен быть небольшим;
• Его оформление, как внутреннее, так и внешнее, должно быть приятно глазу;
• Каждая тема в справочнике должна быть систематизирована и показана на конкретных примерах.

Этьен Безу

Этье́н Безу́, французский математик, член Французской академии наук.

Дата рождения: 31 марта 1730 г

Место рождения: страна Франция, Немур.

Дата смерти:27 сентября 1783.

Научная сфера: теория чисел.

Теорема Безу

  Остаток от деления многочлена  f(x ) на многочлен (x-c) равен   f(c ).

Степень остатка меньше 1, следовательно, остаток — константа. Пусть r-остаток

Это равенство верно при любых значениях х, положим х = а

Что и требовалось доказать

Важнейшим следствием теоремы Безу является то, что корни целочисленного многочлена являются делителями его свободного члена

Горнер Уильям Джордж

Горнер Уильям Джордж (1786 - 1837) ­ — ­ английский математик. Родился  в городе Бристоль в Англии. Получил образование в Кингствудской школе Бристоля. Основал свою собственную школу в 1809 году в Бате.

Многочлены от одной переменной

р(x) = a n x n + a n-1 x n-1 +…+ a 3 x 3 + a 2 x 2 + a 1 x + a o

- стандартный вид многочлена р(х)

a n x n – старший член многочлена р(х)

a n – коэффициент при старшем члене

n – степень многочлена

a о – свободный член многочлена р(х)

Если a n = 1 , то многочлен р(х) называется приведенным

Если a n ≠ 1 , то многочлен р(х) называется неприведенным

Свойства делимости многочленов

1. Если многочлен P( x ) делится на многочлен Q( x ), а многочлен Q( x ) делится на многочлен M( x ) , то многочлен P( x ) делитcя на многочлен M( x )

2. Если многочлены P( x ) и Q( x ) делятся на многочлен M( x ), то многочлены

P( x ) + Q( x ) и P( x )  Q( x ) делятся на многочлен M( x )

• Если P(x) делится на Q(x); а T(x) – произвольный многочлен; то P(x) . T(x) делится на Q(x); 

4. Если ненулевой многочлен P(x) делится на Q(x), то deg P(x) ≥ deg Q(x),где deg(Р(x) и Q(x)-степени этих многочленов.

5. Еесли deg P(x) = deg Q(x); то P(x) делится на Q(x) тогда и только тогда, когда эти многочлены пропорциональны.

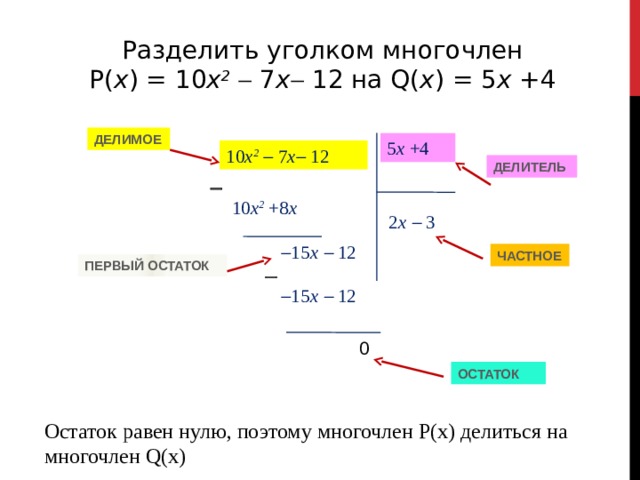
Разделить уголком многочлен

P( x ) = 10 x 2  7 х  12 на Q( x ) = 5 х +4

ДЕЛИМОЕ

5 х +4

10 x 2  7 х  12

ДЕЛИТЕЛЬ



10 x 2 +8 х

2 х  3

 15 х  12

ЧАСТНОЕ

ПЕРВЫЙ ОСТАТОК



 15 х  12

0

ОСТАТОК

Остаток равен нулю, поэтому многочлен P(x) делиться на многочлен Q(x)

Пример : Разделить многочлен P( x ) = 3 x 4 + 2 x 2 – 1 на многочлен

Q( x ) = x 2 + x .

3 x 4 + 2 x 2 – 1

x 2 + x



3 x 4 + 3 x 3

3 x 2 – 3 х + 5

– 3 x 3 + 2 х 2 – 1



– 3 x 3 – 3 x 2

5 x 2 – 1



5 x 2 + 5 x

– 5 x – 1

Степень остатка – 5 x – 1 меньше степени делителя x 2 + x, деление закончено.

Ответ: 3 x 2 – 3 х + 5  частное, – 5 x – 1  остаток.

Пример

2 п 2 -11 п +13

При каких натуральных значениях п выражение

п-3

является целым числом?

Решение.

Разделим числитель дроби на знаменатель с остатком:

_2 п2 -11 п +13 п -3

2 п2 -6 п 2 п -5

_-5 п +13

-5 п +15

-2

2

Таким образом, исходное выражение равно 2 п -5- , что

п -3

является целым числом тогда и только тогда, когда 2

нацело делится на п -3 . поскольку целыми делителями

числа 2 являются числа -2,

-1, 1, 2 и только они, получаем п =1, 2, 4, 5.

Ответ: п =1, 2, 4, 5.

Алгоритм деления многочленов «столбиком»

• Расположить делимое и делитель в убывающих степенях х ;
• Разделить старший член делимого на старший член делителя; затем полученный одночлен сделать первым членом частного;
• Первый член частного умножить на делитель, результат вычесть из делимого; полученная в результате разница является первым остатком;
• Чтобы получить следующий член частного, нужно с первым остатком поступить так, как поступали с делимым и делителем в пунктах 2 и 3.
• Это следует продолжать до тех пор, пока не будет получен остаток, равный нулю или остаток, степень которого меньше степени делителя.

18

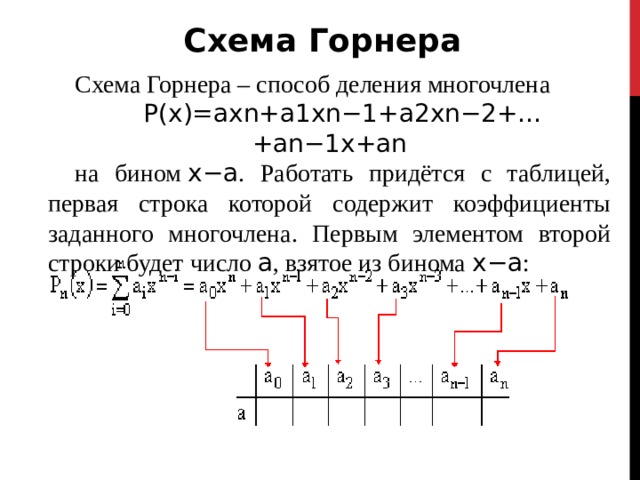
Схема Горнера

Схема Горнера – способ деления многочлена

P ( x )= axn + a 1 xn −1+ a 2 xn −2+…+ an −1 x + an

на бином  x − a . Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена. Первым элементом второй строки будет число  a , взятое из бинома  x − a :

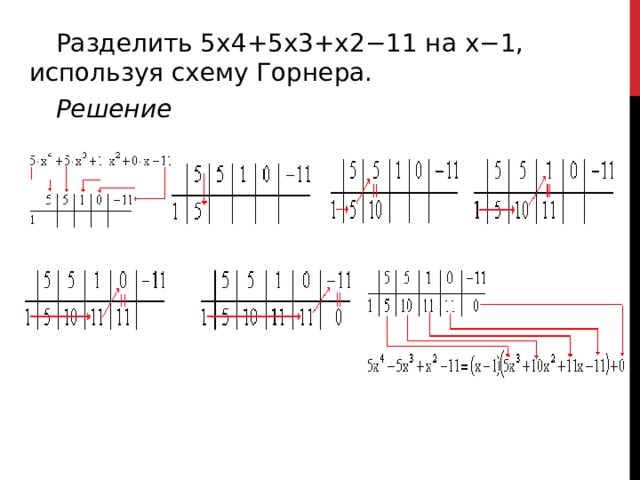
Разделить 5x4+5x3+x2−11 на x−1, используя схему Горнера.

Решение

Можно записывать решение покороче при помощи таблицы:

5 x 4 +5 x 3 + x 2 −11  делим на х – 1

1*5 + 5 = 10

1*10 + 1 = 11

1* 11 + 0 = 11

1* 11 + (-11) = 0

Записать ответ: 5 x 4 +5 x 3 + x 2 −11  = ( 5 x 3 +10 x 2 +11 x +11 ) (х – 1) + 0

1

5

5

5

1

10

0

11

11

-11

0

5 x 4 + 5 x 3 + x 2 − 11  = ( 5 x 3 + 10 x 2 + 11 x + 11 ) (х – 1) + 0

Решение уравнений

Найдите корни уравнения    х 3  + 4 х 2  +  х  – 6 = 0.

Находим делители свободного члена ±1; ± 2; ± 3; ± 6 . Один из корней многочлена будет равен 1. Корнем многочлена является 1, а значит исходный многочлен должен делиться на

  х-1. Строим таблицу для применения схемы Горнера:

1

1

4

1

1

1 ∙ 1 + 4 = 5

–   6

5 ∙ 1 + 1 = 6

6 ∙ 1 + (– 6) = 0

Итак, коэффициенты частного – числа 1, 5, 6, а остаток  r  = 0. Значит,

х 3  + 4 х 2  +  х  – 6 = ( х  – 1) ( х 2  + 5 х  + 6) = 0

Отсюда:  х  – 1 = 0 или  х 2  + 5 х  + 6 = 0; х  = 1,  х 1  = – 2;    х 2  = –3.

     Ответ: 1, – 2, – 3.

Разложение на множители

Разложить на множители многочлен 2х2 – 3х-5.

Данный многочлен имеет целые коэффициенты. Если целое число является корнем этого многочлена, то оно является делителем числа 5. Таким образом, если у данного многочлена есть целые корни, то это могут быть только числа ±1; ±5. Непосредственной проверкой убеждаемся, что число -1 является корнем этого многочлена.

Воспользуемся схемой Горнера :

-1

2

-3

2

0

-5

-5

-5

0

2х2 -3х -5 = (2х -5) (х + 1)

Пример

Разложить многочлен: х 3 − 3х 2 − 10х + 24

Будем искать корни среди делителей свободного коэффициента 24 : ± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24 .

р(1) = 12 ≠ 0 , р(−1) = 30 ≠ 0 , р(2) = 0 .

Значит х = 2 – корень многочлена р(х) . С помощью схемы Горнера найдем частное q(x) :

1

− 3

− 10

24

2

2  (−12)+24

2  1+(−3)

2  (−1)−10

1

− 1

− 12

1

0

х 3 − 3х 2 − 10х + 24 =

(х – 2)(х 2 − х − 12) =

= (х – 2)(х − 4)(х + 3)

Сокращение дробей

Пользуясь делением многочлена на двучлен сократить дробь

(2x 3 +7x 2 -28x+12)/ (x-1/2)

2x 3 +7x 2 -28x+12

x-1/2

=

2(x-1/2)(x+6)(x-2)

=

(x-1/2)

2(x+6)(x-2)

1

=

2(x+6)(x-2)

Преимущества для решения задач новым методом – методом деления многочленов

• Время на разложение на множители алгебраического выражения в среднем уменьшается в среднем на 6 минут
• Применение данного метода не требует запоминания формул сокращенного умножения

3. Применение данного метода не требует знания метода группировки и способа вынесения общего множителя за скобки

проблемы применения данного метода:

• Проверка условий делимости требует дополнительных временных затрат
• Алгоритм деления многочленов труден к восприятию
• Применение только метода деления многочленов не способствует запоминанию традиционных методов решения.

Заключение

Рассмотренные понятия позволяют дать определение теории делимости многочленов: теория делимости многочленов - это математическая наука, изучающая деление одного многочлена на другой.

      Данная работа помогает разобраться в сущности теории делимости многочленов, научиться решать с помощью нее математические уравнения, понять в каких областях она может применяться. Материалы работы можно использовать на математических кружках, спецкурсах, факультативах.

Литературный обзор:

1. Алгебра. 8 класс. В 2 ч. Ч. 1. Задачник для учащихся общеобразовательных учреждений / [А. Г. Мордкович и др.] ; под ред. А. Г. Мордковича. – 12-е изд., испр. И доп. – М. : Мнемозина, 2010. – 271 с. : ил.

2. М.Я. Выгодский Справочник по элементарной математике: - М., 1972., 416 стр. с илл.

. Энциклопедия онлайн «Википедия»: статья о делимости многочленов.

5.  sbiryukova.narod.ru: статья о делимости многочленов.

4.   www.ref.by/refs : статья о теореме Безу.

6.  ega-math.narod.ru: статья о вычислениях многочленов

Спасибо за внимание !

Желаю успехов в

изучении математики!