
Mavzu: Chiziqli bir jinsli bo’lgan oddiy diferensial tenglamalarning normal sistemasi
Farg’ona 2022
MUNDARIJA
KIRISH 3
I-BOB. CHIZIQLI BIR JINSLI BO’LGAN ODDIY DIFFERENSIAL TENGLAMALARNING NORMAL SISTEMASI. 6
1.1 Oddiy differensial tenglamalarning normal sistemasi. Umumiy tushunchalar 6
1.2 Differensial tenglamalarning normal sistemasi 8
1.3 Normal sistemaning yechimining mavjudligi va yagonaligi 11
1.4 Chiziqli bir jinsli bo’lgan differensial tenglamalarning normal sistemasi 22
XULOSA……………………………………………………………………………………………………………….26
FOYDALANILGAN ADABIYOTLAR…………………………………………...30
KIRISH
Farzandlarimizni mustaqil fikirlaydigan, zamonaviy bilim va kasb-hunarlarni chuqur egallaydigan, mustahkam hayotiy pozitsiyaga ega, chinakam vatanparvar insonlar sifatida tarbiyalash biz uchun xamisha dolzarb masala hisoblanadi.
SH.Mirziyoyev
Ta`lim sohasidagi xalqaro aloqalar davlat tashqi siyosiy faoliyatining tarkibiy qismi hisoblanadi. Oliy kasb-hunar maktabining rivojlanishi uning xalqaro faoliyatini takomillashtirishni nazarda tutadi, bu rivojlanishning muhim elementi hisoblanadi. Ta`lim sohasida xalqaro faoliyatni rivojlantirishdan ko`zlangan umumiy maqsad nafaqat milliy, balki xalqaro miqyosda ham akademik va ilmiy reytinglarni oshirish, o`quv seminarlarini tashkil etish, ilmiy aloqalarni mustahkamlash, professor-o`qituvchilar va talabalarni zamonaviy xorijiy adabiyotlar bilan yaqindan tanishtirishdan iborat. Bugungi kunda eng muhimi, xalqaro tajribani hisobga olgan holda milliy ta`lim tizimini takomillashtirish va nufuzini oshirishdir
O’zbekistоn mustaqillikka erishgan kundan bоshlab o’tgan qisqa vaqt ichida o’zbek xalqi siyosiy – ijtimоiy, iqtisоdiy va madaniy sоhalarda katta yutuqlarga erishdi. O’z tarixiga yangicha tafakkur asоsida yondashish, ulug’ ajdоdlar qоldirgan bоy madaniy, ma'naviy merоsni o’rganish sharafiga muyassar bo’ldi, milliy g’ururi qayta tiklandi. Respublikada ilm-fan, jumladan, matematika fani taraqqiyot bоsqichiga ko’tarilmоqda.
O’tmishdagi riyoziyot (matematika) daxоlarining shuxratini tiklash, ularning g’оyalarini xalq hayotiga tadbiq etishdek ulug’ ishlar amalga оshirilmоqda.
1997 – yil 29 avgust O’zbekistоn Respublikasi Оliy majlisida “Ta’lim to’g’risida” gi qоnunning va “Kadrlar tayyorlash milliy dasturi” ning qabul qilinishi muqaddas zaminimizda yashayotgan har bir insоn va uning baxtu-saоdati, farzandini fazlu-kamоlini ko’rish uchun ulkan imkоniyatlar yaratishga asоs bo’ldi. Mamlakatimizda ta’lim tizimidagi оlib bоrilayotgan islоxоtlarning mazmuni va amalga оshirish muddatlari ushbu qоnunda o’z aksini tоpgan. “Kadrlar tayyorlash milliy dasturi” da ta’kidlanganidek, “Kadrlar tayyorlash tizimi va mazmunini mamlakatning ijtimоiy va iqtisоdiy taraqqiyoti istiqbоllaridan, jamiyat ehtiyojlaridan, fan, madaniyat, texnika va texnоlоgiyaning zamоnaviy yutuqlaridan kelib chiqqan hоlda qayta qurish lоzim”.
avgust O’zbekistоn Respublikasi Оliy majlisida “Ta’lim to’g’risida” gi qоnunning va “Kadrlar tayyorlash milliy dasturi” ning qabul qilinishi muqaddas zaminimizda yashayotgan har bir insоn va uning baxtu-saоdati, farzandini fazlu-kamоlini ko’rish uchun ulkan imkоniyatlar yaratishga asоs bo’ldi. Mamlakatimizda ta’lim tizimidagi оlib bоrilayotgan islоxоtlarning mazmuni va amalga оshirish muddatlari ushbu qоnunda o’z aksini tоpgan. “Kadrlar tayyorlash milliy dasturi” da ta’kidlanganidek, “Kadrlar tayyorlash tizimi va mazmunini mamlakatning ijtimоiy va iqtisоdiy taraqqiyoti istiqbоllaridan, jamiyat ehtiyojlaridan, fan, madaniyat, texnika va texnоlоgiyaning zamоnaviy yutuqlaridan kelib chiqqan hоlda qayta qurish lоzim”.
Birinchi Prezidentimiz Islоm Karimоv tashabbusi bilan ishlab chiqilgan, “Kadrlar tayyorlash milliy dasturi” ning hayotga tadbiq etilishi tufayli uzluksiz ta'lim tizimi muntazam yangilanayotgani va takоmillashayotgani, ta'lim muassasalarining zamоnaviy mоddiy-texnik va o’quv bazasini shakllantirish va mustahkamlash, ta’lim-tarbiya jarayoniga yangi standartlar, ilg’оr pedagоgik va axbоrоt texnоlоgiyalarini jоriy etish bоrasida keng ko’lamli ishlar amalga оshirilayotir.
Vatanimizning kelajagi, xalqimizning ertangi kuni, mamlakatimizning jaxоn hamjamiyatidagi оbro - e’tibоri, avvalambоr, farzandlarimizning unib - o’sib, ulg’ayib, qanday insоn bo’lib hayotga kirib bоrishiga bоg’liqdir. Biz bunday haqiqatni hech qachоn unutmasligimiz kerak.
Differensial tenglamalar fizika, mexanika, differensial geometriya, variyasion hisob, issiqlik texnikasi, elektrotexnika, kimyo, biologiya va iqtisod kabi fanlarda keng qullaniladi.
Bu fanlarda uchraydigan ko’plab jarayonlar differensial tenglamalar yordamida tavsiflanadi. Shu tenglamalarni o’rganish bilan tegishli jarayonlar haqida biror ma’lumotga, tasavvurga ega bo’lamiz.
Differensial tenglamalar o’rganilayotgan jarayonning matematik modelidan iborat bo’ladi. Bu model qancha mukammal bo’lsa, differensial tenglamalarni o’rganish natijasida olingan ma’lumotlar jarayonlarni shuncha to’la tavsiflaydi. Shuni aytib o’tish kerakim, tabiatda uchraydigan turli jarayonlar bir xil differensial tenglamalar bilan tavsiflanishi mumkin.
Differensial tenglamalar va ularning sistemalari juda ko’p dinamik jarayonlarning matematik modellarini qurishda qo’llaniladi. Bunday differensial tenglamalar yoki ularning sistemalari yechimlari to’plami cheksiz bo’lib, yechimlar bir-biridan o’zgarmas sonlarga farq qiladi.
Kurs ishining dolzarbligi: Differensial tenglamalar hozirgi zamon matematikasining muhim va murakkab tarmoalaridan biri hisoblanadi. Differensial tenglamlar yordamida bir qator nazariy va amaliy masalalr hal qilinadi. Ushbu kurs ishi chiziqli bir jinsli bo’lmagan oddiy differensial tenglamalarning normal sistemasini o’rganishga olib keladi. Kurs ishida masalalar qisqacha bayon etilib, turli usullar bilan tushuntirishga e’tibor qaratilgan.
Kurs ishining maqsadi: Ushbu kurs ishida chiziqli bir jinsli bo’lmagan oddiy differensial tenglamalarning normal sistemasini o’rganib chiqish va yoritishdir.
Kurs ishining ob’ekti: Chiziqli bir jinsli bo’lmagan oddiy differensial tenglamalarning normal sistemasi bo’limi bo’yicha o’quvchilarga ma’lumot berish.
Kurs ishining predmeti: Chiziqli bir jinsli bo’lmagan oddiy differensial tenglamalarning normal sistemasi bo’limini Koshi masalasi, Lipshits shartlari va Pikar teoremasidan foydalanib mavzuni yorita olishdir.
Kurs ishi tuzilishi va hajmi. Kurs ishi kirish, asosiy qism 4 ta mavzu, xulosa va foydalanilgan adabiyotlardan iborat.
I-BOB. CHIZIQLI BIR JINSLI BO’LGAN ODDIY DIFFERENSIAL TENGLAMALARNING NORMAL SISTEMASI. 1.1 Oddiy differensial tenglamalarning normal sistemasi. Umumiy tushunchalar

 tartibli oddiy differensial tenglamalar bilan tanishganmiz. Unda noma’lum bitta
tartibli oddiy differensial tenglamalar bilan tanishganmiz. Unda noma’lum bitta  bo’lib, tenglamada uning hosilalari ishtirok etar edi. Agar noma’lum funksiyalar
bo’lib, tenglamada uning hosilalari ishtirok etar edi. Agar noma’lum funksiyalar  ta bo’lib, ular bitta erkli o’zgaruvchining funksiyalari bo’lib, quyidagi
ta bo’lib, ular bitta erkli o’zgaruvchining funksiyalari bo’lib, quyidagi  ta differensial tenglamani ko’rish mumkin:
ta differensial tenglamani ko’rish mumkin:

 (2.1)
(2.1)
Bunda  funksiyalar
funksiyalar  o’lchovli fazoning biror
o’lchovli fazoning biror  soxasida aniqlangan. Bu (2.1) sistema
soxasida aniqlangan. Bu (2.1) sistema  hosilalarga nisbatan yechiladi deb qarasak, ushbu
hosilalarga nisbatan yechiladi deb qarasak, ushbu
 (2.2)
(2.2)
sistemaga kelamiz. Ravshanki  funksiyalar
funksiyalar  o’lchovli fazoning biror
o’lchovli fazoning biror  sohasida aniqlangan deb qarash lozim. Shu (2.2) tenglamalar sistemasi differensial tenglamalarning kanonik sistemasi deb ataladi. Kanonik sistemalarni yana boshqa ko’rinishda ham yozish mumkin. Differensial tenglamalarning ikki sistemasi bir xil yechimlarga ega bo’lsa, bu sistemalar ekvivalent deyiladi. Endi kanonik sistemalarni unga ekvivalent sistema ko’rinishiga keltiramiz:
sohasida aniqlangan deb qarash lozim. Shu (2.2) tenglamalar sistemasi differensial tenglamalarning kanonik sistemasi deb ataladi. Kanonik sistemalarni yana boshqa ko’rinishda ham yozish mumkin. Differensial tenglamalarning ikki sistemasi bir xil yechimlarga ega bo’lsa, bu sistemalar ekvivalent deyiladi. Endi kanonik sistemalarni unga ekvivalent sistema ko’rinishiga keltiramiz:
(2.2)sistemada bunday belgilanishlarni bajaramiz:









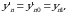


Belgilanishlar natijasida  tan
tan  noma’lum funksiyalar o’rniga
noma’lum funksiyalar o’rniga  ta noma’lum funksiyaga egamiz. Berilgan (2.2) sistema bunday yoziladi:
ta noma’lum funksiyaga egamiz. Berilgan (2.2) sistema bunday yoziladi:





. . . . . . . . . .





Biz birinchi tartibli differensial tenglamalar sistemasiga egamiz. Bunday sistemalar tekshirish, integrallash uchun ancha qulay xususiyatlarga ega. Biz yuqorida ushbu
 (2.3)
(2.3)
Sistemaning xususiy ko’rinishiga keldik. Ushbu (2.3) sistema ko’rinishida 
 tartibli differensial tenglamani, ya’ni ushbu
tartibli differensial tenglamani, ya’ni ushbu

tenglamani ham yozish mumkin. Uning uchun





Belgilashlarni bajarish yetarli.
Shu munosabat bilan biz asosan (2.3)
1.2 Differensial tenglamalarning normal sistemasi
Differentsial tenglamalarning ushbu
 (2.1)
(2.1)
sistemesi tenglamalarning normal sistemasi deyiladi. Bu sistemada  lar
lar  ning nomaʼlum funksiyalari ,
ning nomaʼlum funksiyalari ,  lar esa
lar esa  o’chovli fazoning biror
o’chovli fazoning biror  sohasida aniqlangan va uzluksiz funksiyalar. Аgar
sohasida aniqlangan va uzluksiz funksiyalar. Аgar  intervalda aniqlangan funksiyalarning
intervalda aniqlangan funksiyalarning  sistemasi uchun
sistemasi uchun
1. 
2. 

3. 

shartlar bajarilsa, funktsiyalarning berigan sistemasi (2.1) sistemaning  intervalda aniqlangan yechimi deyiladi.
intervalda aniqlangan yechimi deyiladi.
Аgar  lar ixtiyoriy berilgan oʼz- garmas sonlar bo’lib,
lar ixtiyoriy berilgan oʼz- garmas sonlar bo’lib,  bo’lsa, (2.1) snstemaning
bo’lsa, (2.1) snstemaning
 (2.2)
(2.2)
shartlarni qanoptlantiradigan yechimini topish masalasi (2.1) snstema uchun Koshi masalisi deynladi.  miqdorlar boshlang’ich qiymatlar, (2.2) shartlar esa boshilanich shartlar deb yuritiladi. Yechimniig grafigi
miqdorlar boshlang’ich qiymatlar, (2.2) shartlar esa boshilanich shartlar deb yuritiladi. Yechimniig grafigi  o’lchovli fazoda egri chiziqni ifodalaydi va u integral egri chiziq deb ataladi. Koshi masalasining geometrik maʼnosi
o’lchovli fazoda egri chiziqni ifodalaydi va u integral egri chiziq deb ataladi. Koshi masalasining geometrik maʼnosi  o’lchovli fazonnig
o’lchovli fazonnig  sohasiga tegishli
sohasiga tegishli  nuqtasidan oʼtadigan integral egri chizikni topishdan iboratdir. (2.1) sistemada
nuqtasidan oʼtadigan integral egri chizikni topishdan iboratdir. (2.1) sistemada  funktsiyalar baʼzi shartlarni qanoatlantirsa, berilgan nuqta uchun Koshi masalasi yagona yechimga ega bo’ladi. Bunday yechim xususiy yechim deyiladi.
funktsiyalar baʼzi shartlarni qanoatlantirsa, berilgan nuqta uchun Koshi masalasi yagona yechimga ega bo’ladi. Bunday yechim xususiy yechim deyiladi.
Аgar  ta ixtiyoriy o’zgarmasga bog’liq bo’lgan
ta ixtiyoriy o’zgarmasga bog’liq bo’lgan
 (2.3)
(2.3)
funksiyalar sistemesi uchun (bu yerda  )
)
1) funksiyalarning (2.3) skstemasi (2.1) yechimi bulsa;
2) (2.1) sistemaning ixtiyoriy xususiy yechimi  , larning aniq
, larning aniq  qiymatlarida (2.3) dan hosil bo’lsa, boshqacha aytganda, berilgan boshlang’ich qiymatlar uchun quyidagi
qiymatlarida (2.3) dan hosil bo’lsa, boshqacha aytganda, berilgan boshlang’ich qiymatlar uchun quyidagi
 (2.4)
(2.4)
sistema  larga nisbatan yagona yechimga ega boʼlsa, funksiyalarning (2.3) sistemӕsi (2.1) sistemaning umumiy yechimi deyiladi.
larga nisbatan yagona yechimga ega boʼlsa, funksiyalarning (2.3) sistemӕsi (2.1) sistemaning umumiy yechimi deyiladi.
(2.1) sistemaning barcha yechimlarini topish uni integrallash deyiladi.
Misol. Ushbu

sistema uchun 
 funksiyalar sistemasi yechim va
funksiyalar sistemasi yechim va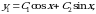
 sistema esa umumiy yechim ekaniga ishonch xosil kilish qiyin emas. Umumiy yechimda
sistema esa umumiy yechim ekaniga ishonch xosil kilish qiyin emas. Umumiy yechimda 
 bo’lganda keltirilgan xususiy yechim hosil bo’ladi.
bo’lganda keltirilgan xususiy yechim hosil bo’ladi.
Ko’pincha (2.1), (2.2), (2.3) va (2.4) lar uchun vektor ko’rinishidagi yozuv qulay bo’ladi. Agar 
 ,
,  belgilashlar kiritsak,
belgilashlar kiritsak,
ushbu






qulay munosabatlarni hosil qilamiz. Bunday belgilashlarda yuqoridagi misol uchun xususiy yechim  umumiy yechim
umumiy yechim

koʼrishtda yozilishi mumkin
1.3 Normal sistemaning yechimining mavjudligi va yagonaligi
Biz mazkur bobinig 1- rejasida tartibli differensial tenglamalar uchun. 2-rejasida esa differentsial tenglamalarning normal sistemasi uchun dastlabki tushunchalarni kiritdik. Keyngi rejalarda kuramizki,  -tartibli tenglama
-tartibli tenglama  ta birinchi tartibli tenglamalarning normal sistemasiga keltirilishini va ularning yechimlari orasidagi bog’lanishni tushuntirish mumkin. Shu sababli avval normal sistema yechimining mavjudligi va yagonaligi haqidagi Pikar teoremasini isbotlab, undan xususiy holda
ta birinchi tartibli tenglamalarning normal sistemasiga keltirilishini va ularning yechimlari orasidagi bog’lanishni tushuntirish mumkin. Shu sababli avval normal sistema yechimining mavjudligi va yagonaligi haqidagi Pikar teoremasini isbotlab, undan xususiy holda  -tartibli tenglama uchun Pikar teoremasini keltirib chiqaramiz.
-tartibli tenglama uchun Pikar teoremasini keltirib chiqaramiz.
3.1-teorema (Pikar teoremasi). Аgar (2.1) sistema uchun 
 boshlang’ich qiymatlar berilgan boʼlib:
boshlang’ich qiymatlar berilgan boʼlib:
 funksiyalar ushbu
funksiyalar ushbu
 (3.1)
(3.1)
yopik sohada uzluksiz (demak, shu sohada chegaralangan boʼladi,  ya’ni bo’lsa;
ya’ni bo’lsa;
 sohada , funksiyalar
sohada , funksiyalar  lar bo’yicha Lipshits shartini qanoatlantirsa, yaʼni ixtiyriy ikki
lar bo’yicha Lipshits shartini qanoatlantirsa, yaʼni ixtiyriy ikki  va
va  nuqta uchun
nuqta uchun
 (3.2)
(3.2)
tengsizliklar o’rinli bo’lsa, u holda (2.1) sistema  intervalda aniqlangan yagona yechimga ega buladi.
intervalda aniqlangan yagona yechimga ega buladi.
Ta’kidlab o’tamizki, agar  , funktsiyalar
, funktsiyalar  lar bo’yicha
lar bo’yicha  sohada uzluksiz differensiallanuvchi bo’lsa, u holda chekli orttirmalar haqidagi teoremaga ko'ra (3.2) shart bajariladi. Haqiqatan, yuqorida aytigan faraz o’rinli bo'lsa, quyidagiga ega bo’lamiz:
sohada uzluksiz differensiallanuvchi bo’lsa, u holda chekli orttirmalar haqidagi teoremaga ko'ra (3.2) shart bajariladi. Haqiqatan, yuqorida aytigan faraz o’rinli bo'lsa, quyidagiga ega bo’lamiz:



Endi. 3.1-teoremaning isbotiga o'tamiz. Birinchi tartibli differensial tenglama uchun 1-bobda isbotlangan Pikar teoremgsidagi kabi bu teoremani ham ketma-ket yakinlashish metodi bilan isbotlaymiz. zarur tasdiqni keltiramiz.
1. Ekvivalentlik lemmasi (Normal sistema uchun). Agar  vektor funksiya
vektor funksiya  , nuqtani o’z ichiga olgan biror
, nuqtani o’z ichiga olgan biror  intervalda aniqangan bo’lib (2.1)-(2.2) Koshi masalasining yechimi bo’lsa, holda shu
intervalda aniqangan bo’lib (2.1)-(2.2) Koshi masalasining yechimi bo’lsa, holda shu  vektor-funktsiya
vektor-funktsiya  intervalda ushibu
intervalda ushibu
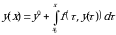 (3.3)
(3.3)
vektor-integral tenglamaning yechimi buladi; aksincha, agar  vektor-fun ksiya
vektor-fun ksiya  intervalda uzluksiz bo’lib, (3.3) vektor tenglamaning yechimi bo’lsa, u holda
intervalda uzluksiz bo’lib, (3.3) vektor tenglamaning yechimi bo’lsa, u holda  vektor-funksiya (2.1) - (2.2) Koshi masalasining yechimi buladi.
vektor-funksiya (2.1) - (2.2) Koshi masalasining yechimi buladi.
Mazkur lemmaning isboti bitta tenglama uchun isbotlangan tegishli lemmaning isbotiga oʼxshash
2. Sistema uchun Pikar teoremasining isboti. Mavjudligi. Yuqorida keltirilgan ekvivalentlik lemmasiga ko’ra (2.6)— (2.7) masala (Koshi masalasi) oʼrniga ushbu
 (3.4)
(3.4)
integral tenglamalar sistemasini yechish masalasini qaraymiz.  intervalda quyidagi vektor-funksiyalar ketma-ketligini kuramiz:
intervalda quyidagi vektor-funksiyalar ketma-ketligini kuramiz:


. . . . . . . . . . . . . .

Vektorida belgilashlardan foydalansak, yuqorida keltirilgan yaqinlashish formulalarini qulayroq yozish mumkin:
 (nolinchi yaqinlashish),
(nolinchi yaqinlashish),
 ,
,
. . . . . . . . . .

Yuqorida ko’rilgan  vektor-funksiyalar
vektor-funksiyalar  intervalda uzluksizligi ravshan. Birinchi va keyingi yaqinlashishlar
intervalda uzluksizligi ravshan. Birinchi va keyingi yaqinlashishlar  bo’lganda
bo’lganda  sohadan chiqib ketmasligini ko'rsatamiz. Haqiqatan
sohadan chiqib ketmasligini ko'rsatamiz. Haqiqatan  ekani ravshan. Sodda hisoblashlar ko'rsatadiki,
ekani ravshan. Sodda hisoblashlar ko'rsatadiki,  bo’lganda
bo’lganda


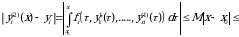

. . . . . . . . . . .


Yuqoridagi munosabatlardan  - ekani kelib chiqadi. Shunday qilib, ushbu
- ekani kelib chiqadi. Shunday qilib, ushbu  vektor-funksiyalar ketma-ketligini hosil qildik. Bu ketma-ketlik
vektor-funksiyalar ketma-ketligini hosil qildik. Bu ketma-ketlik  intervalda tekis yaqinlashuvchi ekanini isbot etamiz. Buning uchun quyidagi
intervalda tekis yaqinlashuvchi ekanini isbot etamiz. Buning uchun quyidagi  ta funksional qatorni tuzamiz:
ta funksional qatorni tuzamiz:
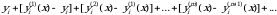
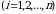 (3.5)
(3.5)
Bu katorning  xususiy yigindisi
xususiy yigindisi  Shuning uchun
Shuning uchun  va
va  vektor ketma-ketlikning tekis yaqinlashuvchi ekanini ko’rsatish uchun (2.5) qatorning tekis yakinlashuvchi ekanini isbot qilish yetarli.
vektor ketma-ketlikning tekis yaqinlashuvchi ekanini ko’rsatish uchun (2.5) qatorning tekis yakinlashuvchi ekanini isbot qilish yetarli.
(3.5) qatorning har bir hadini baholaymiz 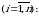






shunga oʼxshash  uchun baho topilgan deb qarab
uchun baho topilgan deb qarab uchun baho topish mumkin:
uchun baho topish mumkin:

Endi  ekanini hisobga olib,
ekanini hisobga olib,

tengsizliklarga ega bo’lamiz. Аgar ushbu

musbat hadli sonli qatorni koʼrsak, bu qator Dalamber alomatiga koʼra yaqinlashuvchi ekaniga ishonch hosil qilamiz. Haqiqatan,

(3.5) qatorning hadlari uzluksiz funksiyalardan iborat. Shuning uchun yuqoridagi mulohazalarga koʼra:
1)  mavjud, 2) bu limit uzluksiz vektor-funksiyadan iborat. Uni
mavjud, 2) bu limit uzluksiz vektor-funksiyadan iborat. Uni  deb belgilaymiz.
deb belgilaymiz.
Topilgan  vektor-funktsiya
vektor-funktsiya  intervalda (2.1) - (2.2) masalaning yechimi ekanini isbotlaymiz. Haqiqatan, avvalo
intervalda (2.1) - (2.2) masalaning yechimi ekanini isbotlaymiz. Haqiqatan, avvalo  ya’ni
ya’ni  vektor-funktsiya (2.2) boshlangʼich shartni kanoatlantiradi. Endi bu
vektor-funktsiya (2.2) boshlangʼich shartni kanoatlantiradi. Endi bu  funktsiya (2.1) sistemaning yechimi ekanini koʼrsatamiz. Ravshanki,
funktsiya (2.1) sistemaning yechimi ekanini koʼrsatamiz. Ravshanki,



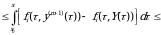

 ketma-ketlik
ketma-ketlik  intervalda
intervalda  funktsiyaga tekis yakinlashuvchiligidan kelib chi qadiki, avvaldan berilgan
funktsiyaga tekis yakinlashuvchiligidan kelib chi qadiki, avvaldan berilgan  uchun shunday N nomer topiladiki,
uchun shunday N nomer topiladiki,  bo’lganda
bo’lganda  intervaldan olingan ixtiyoriy
intervaldan olingan ixtiyoriy  uchun
uchun


tengsizlik bajariladi. Shuning uchun oxirgi baholanayotgan ifoda  dan kichik boʼladi. Demak,
dan kichik boʼladi. Demak,  da limitga oʼtib
da limitga oʼtib

integral temglamani hosil qilamiz. Bundan yuqoridagi tasdiqning toʼg’riligi kelib chiqadi.
Yagonaligi. (2.1) sistemaning (2.2) shartni qanoatlantiradigan yana bitta  (vektor-funksiya) yechimi bor bo’lsin. Uning aniqlanish intervali
(vektor-funksiya) yechimi bor bo’lsin. Uning aniqlanish intervali  boʼlib,
boʼlib,  va
va  larning aniqlanish intervallarining umumiy qismi
larning aniqlanish intervallarining umumiy qismi  bo’lsin deylik. U holda
bo’lsin deylik. U holda  da
da  ekanini ko’rsatamiz. Shartga ko’ra ushbu:
ekanini ko’rsatamiz. Shartga ko’ra ushbu:
 ,
, 
ayniyatlarga egamiz. Keyingi mulohazalarni olib borish uchun vektor-funksiyalarning moduli tushunchasini kiritamiz. U quyidagicha aniqlanadi:

Bundan tashqari maʼlum

Koshi tengsizligini eslatib o’tamiz. Bu tengsizliklar toʼgriligiga ishonch hosil qilish oson. Lagranj ayniyatiga ko’ra topamiz:


Endi  modulni baholaymiz: Yuqoridagi tengsizlikdan va Lipshits shartidan foydalanib topamiz:
modulni baholaymiz: Yuqoridagi tengsizlikdan va Lipshits shartidan foydalanib topamiz:


Oxirgi tengsizlikning ikki tomonini kvadratga oshirib, x bo’yicha 1 dan n gacha yig’indini ko’ramiz:
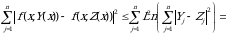

Endi ikki tomonini kvadrat ildizga olsak,

Tengsizlik hosil bo’ladi. Bu tengsizlikdan foydalanib, topamiz:



Shunday qilib,  intervalda
intervalda

tengsizlikka egamiz. Bundan Gronuoll lemmasiga koʼra  da
da  ekani kelib chiqadi. Bu ayniyat
ekani kelib chiqadi. Bu ayniyat  intervalda ham yuqoridagiga oʼxshash isbotlanadi. Bu bilan yagonalik isbotlanadi. Pikar teoremasi ham toʼlik isbot etildi.
intervalda ham yuqoridagiga oʼxshash isbotlanadi. Bu bilan yagonalik isbotlanadi. Pikar teoremasi ham toʼlik isbot etildi.
Eslatib o’tamizki, bitta tenglama uchun yechimni davom ettirish to’g’risida aytilgan mulohazalar bu yerda ham qaytarilishi mumkin.
Chiziqli differentsial tenglamalarning normal sistemasi uchun yechimning mavjudligi va yagonaligi. Birinchi tartibli chiziqli differensial tenglamalarning normal sistemasi deb
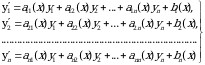 (3.6)
(3.6)
koʼrinishida yozilgan sistemaga aytiladi. Bu yerda 
 funksiyalar biror
funksiyalar biror  intervalda aniqlangan va uzluksiz bo’lgan hol muhimdir. Vektor-matritsa koʼrinishida (3.6) ni
intervalda aniqlangan va uzluksiz bo’lgan hol muhimdir. Vektor-matritsa koʼrinishida (3.6) ni

(3.6) koʼrinishda yozish mumkin, bu yerda  kvadrat matritsadan iborat,
kvadrat matritsadan iborat, va
va  lar ustun-vektorlar.
lar ustun-vektorlar.
Аgar 
 bo’lsa, (3.6) sistema chiziqli bir jinsli, aks holda chiziqli bir jinsli bo’lmagan sistema deyiladi.
bo’lsa, (3.6) sistema chiziqli bir jinsli, aks holda chiziqli bir jinsli bo’lmagan sistema deyiladi.
3.2-teorema. Аgar (3.6) sistema berilgan boʼlib, unda  funksiyalar biror
funksiyalar biror  intervalda uzluksiz,
intervalda uzluksiz,  sonlar ixtiyoriy (ammo
sonlar ixtiyoriy (ammo  ) boshlang’ich qiymatlar bo’lsa, (3.6) sistema
) boshlang’ich qiymatlar bo’lsa, (3.6) sistema

bolilangich shartlarni qanoatlantiradigan va  intervalda aniqlangan yagona yechimga ega bo’ladi.
intervalda aniqlangan yagona yechimga ega bo’ladi.
Isbot. Koʼrilayotgan sistema uchun
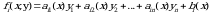
Bu funksiya  aniqlangan va uzluksiz. Bundan tashqari
aniqlangan va uzluksiz. Bundan tashqari  funksiya
funksiya  argumentlar bo’yicha Lipshits shartini qanoatlantiradi. Haqiqatan,
argumentlar bo’yicha Lipshits shartini qanoatlantiradi. Haqiqatan,




Bu yerda

Shunday qilib 3.1-teoremaning barcha shartlari bajariladi, demak,(3.6) sistema berilgan boshlang’ich qiymatlarga ega bo’lgan va I intervalda aniqlangan yagona yechimga ega. Teorema isbot bo’ldi.
1.4 Chiziqli bir jinsli bo’lgan differensial tenglamalarning normal sistemasi
Bir jinsli chiziqli differensial tenglamalar sistemasi berilgan bo’lsin

Quyidagi teoremalarni osonlik bilan isbotlash mumkin.
4.1-TEOREMA . Agar  lar (1) sistemaning yechimlari bo’lsa, u holda
lar (1) sistemaning yechimlari bo’lsa, u holda  lar ham (1) sistemaning yechimlari bo’ladi.
lar ham (1) sistemaning yechimlari bo’ladi.
4.2-TEOREMA. Agar  va
va lar (1) sistemaning yechimlari bo’lsa, u holda
lar (1) sistemaning yechimlari bo’lsa, u holda  lar ham (1) sistemaning yechimlari bo’ladi.
lar ham (1) sistemaning yechimlari bo’ladi.
Faraz etaylik (1) sistemaning xususiy yechimlari
 (2)
(2)
bo’lsin.
Agar bu xususiy yechimlardan tuzilgan
 (3)
(3)
determinant nolga teng bo’lmasa, (2) yechimlar sistemasiga, (1) sistemaning fundamental yechimlar sistemasi (fes) deyiladi.
4.3-TEOREMA. Agar berilgan differensial tenglamalar sistemasining koeffisiyentlari ko’rilayotgan oraliqda uzluksiz bo’lsalar, bu holda sistemaning bu oraliqda aniqlangan fundamental yechimlar sistemasi mavjuddir.
ISBOT. sonlaridann2 tasini shunday tanlab olamizki, ulardan tuzilgan determinant nolga teng bo’lmasin, ya’ni
sonlaridann2 tasini shunday tanlab olamizki, ulardan tuzilgan determinant nolga teng bo’lmasin, ya’ni
 (4)
(4)
(1) sistemaning n2 ta  xususiy yechimlarining shunday tanlab olamizkim, ular
xususiy yechimlarining shunday tanlab olamizkim, ular  da
da  boshlang’ich shartlarni qanoatlantirsin. Xususiy yechimlar ko’rilayotgan oraliqda uzluksiz funksiyalardan iborat. (4) ga asosan ulardan tuzilgan determinant nolga teng bo’lmagani uchun, bu xususiy yechimlar (1) sistemasining fundamental yechimlar sistemasini tashkil etadi.
boshlang’ich shartlarni qanoatlantirsin. Xususiy yechimlar ko’rilayotgan oraliqda uzluksiz funksiyalardan iborat. (4) ga asosan ulardan tuzilgan determinant nolga teng bo’lmagani uchun, bu xususiy yechimlar (1) sistemasining fundamental yechimlar sistemasini tashkil etadi.
4.4-TEOREMA . Agar ko’rilayotgan oraliqning biror x0nuqtasida  bo’lmasa, u holda oraliqning hamma nuqtalarida bulmaydi
bo’lmasa, u holda oraliqning hamma nuqtalarida bulmaydi  .
.
ISBOT.Teoremani isboti uchun (3) determinantning ustun elementlari bo’yicha hosilani olamiz.
Ma’lumki n-tartibli determinantning hosilasi n–ta n-tartibli determinantlar yig’indisiga teng bo’lib, ularning birinchisida faqat birinchi ustun elementlarining hosilasi olinib, qolgan elementlar uz holiga qoladi, ikkinchi determinantida ikkinchi ustun elementlarining hosilasi olinib, qolgan elementlar uz holiga qoladi va xokazo, ya’ni

bundagi 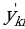 lar o’rniga (1) sistemadan
lar o’rniga (1) sistemadan

qiymatlarni keltirib qo’ysak,

bu oxirgi determinant  bo’lmaganda u nolga teng bo’lib, i=j bo’lganda
bo’lmaganda u nolga teng bo’lib, i=j bo’lganda ga teng bo’ladi.
ga teng bo’ladi.

Bundan

buni har ikkala tomonini [x0,x] oraliqda integrallasak

yoki
 (5)
(5)
Bundan ko’rinadikim, agar  bo’lmasa, u holda
bo’lmasa, u holda  bo’lmaydi.
bo’lmaydi.
(5) ga sistema uchun Ostrogradskiy-Liuvill formulasi deyiladi.
4.5-TEOREMA. Agar  (1) sistemaning fundamental yechimlar sistemasi bo’lsa, u holda (1) sistemaning umumiy yechimi
(1) sistemaning fundamental yechimlar sistemasi bo’lsa, u holda (1) sistemaning umumiy yechimi

dan iborat.
ISBOT. 1 va 2 teoremalarga asosan (6), (1) sistemaning yechimi bo’ladi. Uning umumiy yechim ekanligini ko’rsatish uchun undagi o’zgarmaslarni -ck shundayaniqlab olish mumkin bo’lsakim x=x0 bo’lganda  (7) boshlang’ich shartlarni qanoatlantiruvchi tenglamaning hamma xususiy yechimlarini aniqlash mumkin bo’lsin
(7) boshlang’ich shartlarni qanoatlantiruvchi tenglamaning hamma xususiy yechimlarini aniqlash mumkin bo’lsin  ixtiyoriy son. (7) ni (6) ga olib borib qo’ysak ck ga nisbatan n-ta birjinsli bo’lmagan chiziqli algebraik tenglamalar sistemasiga ega bo’lamiz.
ixtiyoriy son. (7) ni (6) ga olib borib qo’ysak ck ga nisbatan n-ta birjinsli bo’lmagan chiziqli algebraik tenglamalar sistemasiga ega bo’lamiz.
 (8)
(8)
Bu sistemaning asos determinanti Vronskiy determinantidan iborat bo’lib, u nolga teng bo’lmaydi. Chunki shartga asosan  lar (1) sistemaning fundamental yechimlar sistemasidan iborat.
lar (1) sistemaning fundamental yechimlar sistemasidan iborat.
Shuning uchun (8) sistemadan  lar bir qiymatli aniqlanadi
lar bir qiymatli aniqlanadi 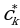 larning bu qiymatlarini (6) ga olib borib qo’ysak boshlang’ich shartlarni qanoatlantiruvchi (1) sistemaning hamma xususiy yechimlarini aniqlash mumkin.
larning bu qiymatlarini (6) ga olib borib qo’ysak boshlang’ich shartlarni qanoatlantiruvchi (1) sistemaning hamma xususiy yechimlarini aniqlash mumkin.
Misol-1. Agar  fundamental yechimlar sistemasi berilgan bo’lsa, unga mos bo’lgan bir jinsli chiziqli differensial tenglamalar sistemasini toping.
fundamental yechimlar sistemasi berilgan bo’lsa, unga mos bo’lgan bir jinsli chiziqli differensial tenglamalar sistemasini toping.
Faraz etaylik izlanayotgan tenglama
 (9)
(9)
bo’lsin.
Bunda  lar aniqlanishi kerak bo’lgan noma’lum funksiyalar.
lar aniqlanishi kerak bo’lgan noma’lum funksiyalar.
Fundamental yechimlar sistemasidan  chisini (9) tenglamaga qo’ysak
chisini (9) tenglamaga qo’ysak

 (10)
(10)
ayniyatiga ega bo’lamiz. Bu esa  larga nisbatan
larga nisbatan  noma’lumli
noma’lumli  ta tenglamalar sistemasidan iboratdir. Bu sistemaninig asos determinanti Vronskiy determinantidan iborat bo’lgani uchun; undan
ta tenglamalar sistemasidan iboratdir. Bu sistemaninig asos determinanti Vronskiy determinantidan iborat bo’lgani uchun; undan  lar bir qiymatli aniqlanadi. Bu topilgan
lar bir qiymatli aniqlanadi. Bu topilgan  -larni (9) tenglama qo’ysak izlangan tenglamaga ega bo’lamiz.
-larni (9) tenglama qo’ysak izlangan tenglamaga ega bo’lamiz.
Buni determinant shaklida ham yozish mumkin

Misol-2y11=x+1 z12=x
y21=2 z22=x
ikki noma’lumli y, z tenglamalarning fundamental yechimlar sistemasi berilgan bo’lsa, tenglamani uzini aniqlash.


yij j-noma’lum funksiya, i-yechimi

XULOSA
Matematik fizika tenglamalari fani klassik mexanika, fizika, gidrodinamika, akustika va boshqa sohalarda bo’ladigan jarayonlarning matematik modellarini yaratish va bu masalalarni yechish usullarini qurish bilan uzviy bog’liq. Bu modellashtirish muayyan jarayonlarni ifodalovchi fizikaviy kattaliklar asosida tenglamalarni keltirib chiqarish bilan xarakterlanadi. Kvant mexanikasi, atom va yadro fizikasi, qattir jismlar nazariyasi, elementar zarralar fizikasi kabi sohalarning rivojlanishi matematik tatqiqotlarning asosini tashkil etadi. Mexanika va fizikaning ko’plab masalalari xususiy hosilali differensial tenglamalarni tadqiq etishga keladi. Shuning uchun xususiy hosilali differensial tenglamalar fani matematik fizikaning zamonaviy holatini o’rganish va tushunish uchun zarur bo’lgan boshlang’ich bilimlarni beradi.
Differensial tenglamalar hozirgi zamon matematikasining muhim va murakkab tarmoalaridan biri hisoblanadi. Differensial tenglamlar yordamida bir qator nazariy va amaliy masalalr hal qilinadi. Ushbu kurs ishi chiziqli bir jinsli bo’lmagan oddiy differensial tenglamalarning normal sistemasini o’rganishga olib keladi. Kurs ishida masalalar qisqacha bayon etilib, turli usullar bilan tushuntirishga e’tibor qaratilgan.
FOYDALANILGAN ADABIYOTLAR
M.S.Salоhiddinоv. Matematik fizika tenglamalari. T. «ФАН», 2004.
M.S.Salоhiddinоv, G.N.Nasriddinоv. Оddiy differensial tenglamalar. T. «O‘qituvchi».1982.
N.Teshabоeva. Matematika fizika metоdlari. T. «O‘qituvchi». 1966.
T.N.Nurimоv. Matematika fizika metоdlari. T. «O‘qituvchi». 1980.
Н.С.Кошляков, Е.Б.Глинер, М.М.Смирнов. Основные дифференци-альные уравнения математической физики. M.GIFML. 1962.
А.Н.Тихонов, А.А.Самарский. Уравнения математической физики. M.«Наука». 1972.
А.В.Бицадзе, Д.Ф.Калиниченко. Сборник задач по уравнениям математической физики. M.«Nauka». 1977.
М.М.Смирнов. Задачи по уравнениям математической физики. M.«Наука». 1975.
Б.М.Будак, А.А.Самарский, А.Н.Тихонов. Сборник задач по матема-тической физике. M.«Наука». 1972.








 avgust O’zbekistоn Respublikasi Оliy majlisida “Ta’lim to’g’risida” gi qоnunning va “Kadrlar tayyorlash milliy dasturi” ning qabul qilinishi muqaddas zaminimizda yashayotgan har bir insоn va uning baxtu-saоdati, farzandini fazlu-kamоlini ko’rish uchun ulkan imkоniyatlar yaratishga asоs bo’ldi. Mamlakatimizda ta’lim tizimidagi оlib bоrilayotgan islоxоtlarning mazmuni va amalga оshirish muddatlari ushbu qоnunda o’z aksini tоpgan. “Kadrlar tayyorlash milliy dasturi” da ta’kidlanganidek, “Kadrlar tayyorlash tizimi va mazmunini mamlakatning ijtimоiy va iqtisоdiy taraqqiyoti istiqbоllaridan, jamiyat ehtiyojlaridan, fan, madaniyat, texnika va texnоlоgiyaning zamоnaviy yutuqlaridan kelib chiqqan hоlda qayta qurish lоzim”.
avgust O’zbekistоn Respublikasi Оliy majlisida “Ta’lim to’g’risida” gi qоnunning va “Kadrlar tayyorlash milliy dasturi” ning qabul qilinishi muqaddas zaminimizda yashayotgan har bir insоn va uning baxtu-saоdati, farzandini fazlu-kamоlini ko’rish uchun ulkan imkоniyatlar yaratishga asоs bo’ldi. Mamlakatimizda ta’lim tizimidagi оlib bоrilayotgan islоxоtlarning mazmuni va amalga оshirish muddatlari ushbu qоnunda o’z aksini tоpgan. “Kadrlar tayyorlash milliy dasturi” da ta’kidlanganidek, “Kadrlar tayyorlash tizimi va mazmunini mamlakatning ijtimоiy va iqtisоdiy taraqqiyoti istiqbоllaridan, jamiyat ehtiyojlaridan, fan, madaniyat, texnika va texnоlоgiyaning zamоnaviy yutuqlaridan kelib chiqqan hоlda qayta qurish lоzim”. 
 bo’lib, tenglamada uning hosilalari ishtirok etar edi. Agar noma’lum funksiyalar
bo’lib, tenglamada uning hosilalari ishtirok etar edi. Agar noma’lum funksiyalar 
 (2.1)
(2.1) funksiyalar
funksiyalar  o’lchovli fazoning biror
o’lchovli fazoning biror  soxasida aniqlangan. Bu (2.1) sistema
soxasida aniqlangan. Bu (2.1) sistema  hosilalarga nisbatan yechiladi deb qarasak, ushbu
hosilalarga nisbatan yechiladi deb qarasak, ushbu (2.2)
(2.2) funksiyalar
funksiyalar  o’lchovli fazoning biror
o’lchovli fazoning biror  sohasida aniqlangan deb qarash lozim. Shu (2.2) tenglamalar sistemasi differensial tenglamalarning kanonik sistemasi deb ataladi. Kanonik sistemalarni yana boshqa ko’rinishda ham yozish mumkin. Differensial tenglamalarning ikki sistemasi bir xil yechimlarga ega bo’lsa, bu sistemalar ekvivalent deyiladi. Endi kanonik sistemalarni unga ekvivalent sistema ko’rinishiga keltiramiz:
sohasida aniqlangan deb qarash lozim. Shu (2.2) tenglamalar sistemasi differensial tenglamalarning kanonik sistemasi deb ataladi. Kanonik sistemalarni yana boshqa ko’rinishda ham yozish mumkin. Differensial tenglamalarning ikki sistemasi bir xil yechimlarga ega bo’lsa, bu sistemalar ekvivalent deyiladi. Endi kanonik sistemalarni unga ekvivalent sistema ko’rinishiga keltiramiz:








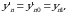


 noma’lum funksiyalar o’rniga
noma’lum funksiyalar o’rniga  ta noma’lum funksiyaga egamiz. Berilgan (2.2) sistema bunday yoziladi:
ta noma’lum funksiyaga egamiz. Berilgan (2.2) sistema bunday yoziladi:








 (2.3)
(2.3)





 lar
lar  ning nomaʼlum funksiyalari ,
ning nomaʼlum funksiyalari ,  lar esa
lar esa  o’chovli fazoning biror
o’chovli fazoning biror  sohasida aniqlangan va uzluksiz funksiyalar. Аgar
sohasida aniqlangan va uzluksiz funksiyalar. Аgar  intervalda aniqlangan funksiyalarning
intervalda aniqlangan funksiyalarning  sistemasi uchun
sistemasi uchun 




 lar ixtiyoriy berilgan oʼz- garmas sonlar bo’lib,
lar ixtiyoriy berilgan oʼz- garmas sonlar bo’lib,  bo’lsa, (2.1) snstemaning
bo’lsa, (2.1) snstemaning  (2.2)
(2.2) miqdorlar boshlang’ich qiymatlar, (2.2) shartlar esa boshilanich shartlar deb yuritiladi. Yechimniig grafigi
miqdorlar boshlang’ich qiymatlar, (2.2) shartlar esa boshilanich shartlar deb yuritiladi. Yechimniig grafigi  nuqtasidan oʼtadigan integral egri chizikni topishdan iboratdir. (2.1) sistemada
nuqtasidan oʼtadigan integral egri chizikni topishdan iboratdir. (2.1) sistemada  funktsiyalar baʼzi shartlarni qanoatlantirsa, berilgan nuqta uchun Koshi masalasi yagona yechimga ega bo’ladi. Bunday yechim xususiy yechim deyiladi.
funktsiyalar baʼzi shartlarni qanoatlantirsa, berilgan nuqta uchun Koshi masalasi yagona yechimga ega bo’ladi. Bunday yechim xususiy yechim deyiladi. (2.3)
(2.3) )
)  , larning aniq
, larning aniq  qiymatlarida (2.3) dan hosil bo’lsa, boshqacha aytganda, berilgan boshlang’ich qiymatlar uchun quyidagi
qiymatlarida (2.3) dan hosil bo’lsa, boshqacha aytganda, berilgan boshlang’ich qiymatlar uchun quyidagi  (2.4)
(2.4) 

 funksiyalar sistemasi yechim va
funksiyalar sistemasi yechim va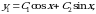
 sistema esa umumiy yechim ekaniga ishonch xosil kilish qiyin emas. Umumiy yechimda
sistema esa umumiy yechim ekaniga ishonch xosil kilish qiyin emas. Umumiy yechimda 
 bo’lganda keltirilgan xususiy yechim hosil bo’ladi.
bo’lganda keltirilgan xususiy yechim hosil bo’ladi. 
 ,
,  belgilashlar kiritsak,
belgilashlar kiritsak,





 umumiy yechim
umumiy yechim 

 boshlang’ich qiymatlar berilgan boʼlib:
boshlang’ich qiymatlar berilgan boʼlib:  (3.1)
(3.1) ya’ni bo’lsa;
ya’ni bo’lsa;  sohada , funksiyalar
sohada , funksiyalar  va
va  nuqta uchun
nuqta uchun (3.2)
(3.2) intervalda aniqlangan yagona yechimga ega buladi.
intervalda aniqlangan yagona yechimga ega buladi.


 vektor funksiya
vektor funksiya  , nuqtani o’z ichiga olgan biror
, nuqtani o’z ichiga olgan biror 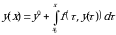 (3.3)
(3.3) (3.4)
(3.4) intervalda quyidagi vektor-funksiyalar ketma-ketligini kuramiz:
intervalda quyidagi vektor-funksiyalar ketma-ketligini kuramiz:


 (nolinchi yaqinlashish),
(nolinchi yaqinlashish),  ,
,
 vektor-funksiyalar
vektor-funksiyalar  sohadan chiqib ketmasligini ko'rsatamiz. Haqiqatan
sohadan chiqib ketmasligini ko'rsatamiz. Haqiqatan  ekani ravshan. Sodda hisoblashlar ko'rsatadiki,
ekani ravshan. Sodda hisoblashlar ko'rsatadiki,  bo’lganda
bo’lganda

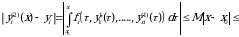

 - ekani kelib chiqadi. Shunday qilib, ushbu
- ekani kelib chiqadi. Shunday qilib, ushbu  vektor-funksiyalar ketma-ketligini hosil qildik. Bu ketma-ketlik
vektor-funksiyalar ketma-ketligini hosil qildik. Bu ketma-ketlik 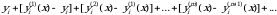
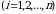 (3.5)
(3.5) xususiy yigindisi
xususiy yigindisi  Shuning uchun
Shuning uchun  va
va  vektor ketma-ketlikning tekis yaqinlashuvchi ekanini ko’rsatish uchun (2.5) qatorning tekis yakinlashuvchi ekanini isbot qilish yetarli.
vektor ketma-ketlikning tekis yaqinlashuvchi ekanini ko’rsatish uchun (2.5) qatorning tekis yakinlashuvchi ekanini isbot qilish yetarli.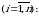






 uchun baho topish mumkin:
uchun baho topish mumkin: 



 mavjud, 2) bu limit uzluksiz vektor-funksiyadan iborat. Uni
mavjud, 2) bu limit uzluksiz vektor-funksiyadan iborat. Uni  deb belgilaymiz.
deb belgilaymiz.  ya’ni
ya’ni  vektor-funktsiya (2.2) boshlangʼich shartni kanoatlantiradi. Endi bu
vektor-funktsiya (2.2) boshlangʼich shartni kanoatlantiradi. Endi bu 


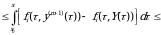

 ketma-ketlik
ketma-ketlik  uchun shunday N nomer topiladiki,
uchun shunday N nomer topiladiki,  bo’lganda
bo’lganda 

 dan kichik boʼladi. Demak,
dan kichik boʼladi. Demak,  da limitga oʼtib
da limitga oʼtib
 (vektor-funksiya) yechimi bor bo’lsin. Uning aniqlanish intervali
(vektor-funksiya) yechimi bor bo’lsin. Uning aniqlanish intervali  larning aniqlanish intervallarining umumiy qismi
larning aniqlanish intervallarining umumiy qismi  ekanini ko’rsatamiz. Shartga ko’ra ushbu:
ekanini ko’rsatamiz. Shartga ko’ra ushbu:  ,
, 




 modulni baholaymiz: Yuqoridagi tengsizlikdan va Lipshits shartidan foydalanib topamiz:
modulni baholaymiz: Yuqoridagi tengsizlikdan va Lipshits shartidan foydalanib topamiz:

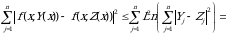





 intervalda
intervalda 
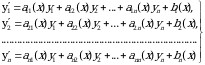 (3.6)
(3.6)
 funksiyalar biror
funksiyalar biror 
 kvadrat matritsadan iborat,
kvadrat matritsadan iborat, va
va  lar ustun-vektorlar.
lar ustun-vektorlar. 
 bo’lsa, (3.6) sistema chiziqli bir jinsli, aks holda chiziqli bir jinsli bo’lmagan sistema deyiladi.
bo’lsa, (3.6) sistema chiziqli bir jinsli, aks holda chiziqli bir jinsli bo’lmagan sistema deyiladi.  funksiyalar biror
funksiyalar biror  sonlar ixtiyoriy (ammo
sonlar ixtiyoriy (ammo  ) boshlang’ich qiymatlar bo’lsa, (3.6) sistema
) boshlang’ich qiymatlar bo’lsa, (3.6) sistema 
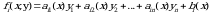
 aniqlangan va uzluksiz. Bundan tashqari
aniqlangan va uzluksiz. Bundan tashqari  funksiya
funksiya 





 (2)
(2) (3)
(3) (4)
(4)





 (5)
(5) 
 (8)
(8) (9)
(9) (10)
(10) noma’lumli
noma’lumli 




















