6 класс Итоговое повторение

Итоговое повторение Математика 6 класс

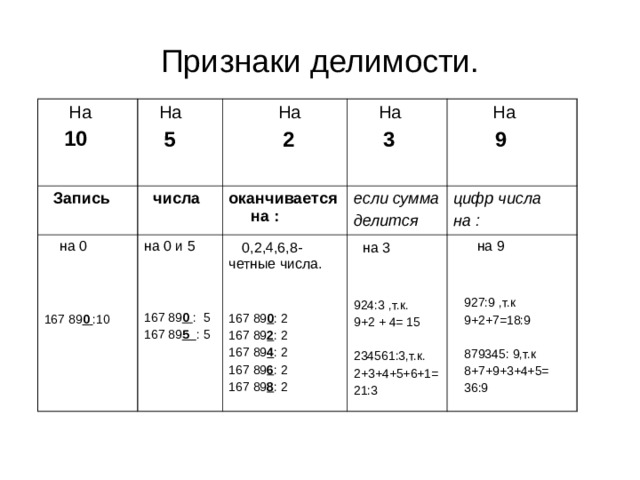
Признаки делимости.

На

10

На

5

Запись

На

2

числа

на 0

167 89 0 :10

На

3

оканчивается на :

на 0 и 5

167 89 0 : 5

167 89 5 : 5

На

9

если сумма

делится

0,2,4,6,8- четные числа.

167 89 0 : 2

167 89 2 : 2

167 89 4 : 2

167 89 6 : 2

167 89 8 : 2

цифр числа

на :

на 3

924:3 ,т.к.

9+2 + 4= 15

234561:3,т.к.

2+3+4+5+6+1=

21:3

на 9

927:9 ,т.к

9+2+7=18:9

879345: 9,т.к

8+7+9+3+4+5=

36:9

Простые и составные числа.

• Делители 7: 1,7

Делители 23: 1,23

2) Делители 8: 1,2,4,8

Делители 10: 1,2,5,10

Простыми числами называют числа, имеющие только 2 делителя – 1 и само число.

Составными числа называют числа, имеющие больше 2 делителей.

Составное число можно разложить (представить в виде произведения) на 2 множителя, каждый из которых больше 1.

Простое число разложить на множители нельзя.

Разложение на простые множители.

• Любое составное число можно разложить на простые множители.
• Множители в ответе записываются в порядке возрастания.
• При разложении больших чисел используют признаки делимости.

Наибольший общий делитель. Взаимно простые числа.

1) Общие делители чисел 48 и 36 :

1, 2, 3, 4, 6, 12

2) Наибольший общий делитель чисел 48 и 36.

НОД (48;36)= 12

3) Нахождение НОД для больших чисел 48;36

1) Делители 48: 1 , 2 , 3 , 4 , 6 , 8, 12 , 16 , 24, 48.

Делители 36 : 1 , 2 , 3 , 4 , 6 ,9 , 12 , 18 , 36.

2) Наибольшее натуральное число на которое данные числа делятся без остатка.

Числа 24 и 35 взаимно простые, т.к.у них один общий делитель –число 1.

• Разлагаем числа на простые множители.
• Из разложения 1 числа ,вычеркиваем множители, которых нет в разложении

2 числа.

Наименьшее общее кратное

НОК (75;60)= 300

Первый способ (устно)

1) Берём большее число – 75

Наименьшее натуральное число, которое кратно (т.е делится) 75 и 60

• 75 на 60 не делится .
• 150 на 60 не делится .
• 265 на 60 не делится.
• 300 на 60 делится.

Второй способ (для больших чисел)

Выписываем разложение большего числа, добавляем недостающие множители.

Находим произведение

НОК (75;60) =300

Основной свойство дроби.

1)

1)

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

2) Числитель и знаменатель умножаем на число 5.

- это различные записи одного и того же числа.

Сокращение дробей.

1)

НОД (15; 20) = 5

2)

- несократимая дробь.

3)

Числитель и знаменатель разделить на общий делитель.

НОД(3;4)=1,т.е числа 3 и 4 взаимно простые.

27: 9 =3

18 : 9 = 2

5 : 5 =1

10 : 5 =2

Приведение дробей к общему знаменателю.

Находим дополнительный множитель.

8:4 =2

2)

привести к НОЗ

1. НОК(4;6)= 12

• 12 : 4 = 3

1.Найти НОК знаменателей

2. Находим дополнительный множитель для каждой дроби.

Обычно дроби приводят к наименьшему общему знаменателю (НОЗ).Он равен наименьшему общему знаменателю данных дробей.

3. 12 : 6 = 2

Задача на движение.

S = vt , где S - путь, v - скорость, t - время.

v

1 электропоезд

t

x + 5

2 электропоезд

s

2

x

(x +5)2

2

2x

Пусть x км / ч скорость 2 электропоезда, т.к по условию два электропоезда прошли вместе 210 км.

Составляем уравнение :

( x+5)2 + 2x=210

2x + 10 + 2x = 210

4x +10 = 210

4x = 210 – 10

4x = 200

x= 200 : 4

x= 50

50 км / ч скорость 1 электропоезда

50 + 5 = 55 км / ч

55 км / ч скорость 2 электропоезда

Ответ: 50 км / ч, 55 км / ч.

Сравнение ,сложение и вычитание дробей с разными знаменателями.

Для примеров

а) , б) ,в)

А) Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем.

Б) Складываем числители, а знаменатель тот же .

В) Из числителя уменьшаемого вычитаем числитель вычитаемого, знаменатель тот же.

Сравнение дробей с одинаковыми числителями.

Пятая часть пирога больше, чем седьмая.

Сложение и вычитание смешанных чисел

• Складываем целые части.

16 + 19 = 35

2. Складываем дробные части.

1) 5+ 3= 8

2) Складываем дробные части .

3) Исключаем целую часть.

.

Вычитание смешанных чисел.

1) У 3 целых занимаем 1 целую и представляем её в виде дроби со знаменателем 6.

Находим НОК ( 9;6) = 18

Находим дополнительные множители.

18: 9 = 2

18: 6 = 3

Выполняем вычитание целых и дробных частей.

НОК ( 9;6) = 18

Умножение дробей.

1) Умножаем дробь на число

А) 5 = 5

1

( Целое число представить в виде дроби со знаменателем 1)

Б) Умножаем числитель и знаменатель, первое произведение записываем в числитель, второе в знаменатель.

См б)

Сократим дробь на 7.

Умножение смешанных чисел.

S=vt, где S– путь, v- скорость , t - время.

Найти S (путь) .

• Представим числа в виде неправильной дроби.

• Умножаем.
• Сократим дробь.
• Исключаем целое число.

Нахождение дроби от числа.

1)

2)

1) Чтобы найти дробь от числа, нужно число умножить на дробь.

20 = 20

1

• Число имеет наименование.( км, кг, минуты, секунды и т.д.)

Применение распределительного свойства умножения .

1) Распределительное св-во умножения .

( a + b )c = ac + bc

2) ( a – b )c = ac - bc

Примеры:

3)

4)

5)

Относительно сложения ( умножаем каждое слагаемое на c )

Относительно вычитания (умножаем на c уменьшаемое и вычитаемое )

Общий множитель 2 выносим за скобки.

7

Сложим 5 3 + 1 5 = 6 8 = 7

8 8 8

Выносим множитель а за скобки.

Затем находим НОК( 8; 4 )=8

Взаимно обратные числа.

1) 8 и 15 , т. к

15 8

• 7 и 1 , т . к

1) Числа, взаимно обратные, если их произведение равно 1.

7

3)

2) 7 = 7

1

Деление .

Примеры :

Рабочее правило :

Деление заменяем умножением на дробь, обратную делителю.

6 и 1 – взаимно обратные числа.

6

Нахождение числа по его дроби.

2) 0,8 это 2400 га

2400 : 0,8 = 24000 : 8 = 3000 га

Ответ : 3000 га

3) 7% это 98 деталей

0,07 это 98 деталей

98 : 0,07 = 9800: 7 = 1400 деталей

Ответ : 1400 деталей.

• Нужно число разделить на дробь.

Число имеет наименование.

800 = 800

1

2 и 5 - взаимно обратные числа.

5 2

• Число делим на дробь.

Переносим запятую и в делимом, и в делителе на 1 знак вправо.

• 1% = 0,01

7% = 0,07

Дробные выражения.

1) 2 : 3 = 2

3

Дробное выражение- частное двух чисел или выражений ( знак деления заменяем чертой дроби)

2) При выполнении действий пользуемся правилами для обыкновенной дробей.

1 3 = 7

4 4

НОК ( 7; 14) = 14

Пропорции.

• а) 3,6 : 1,2 = 6,3 : 2,1

3 = 3

б) 3,6 = 6,3

1,2 2,1

2) a : b = c : d

a = c

b d

3) a и d – крайние члены пропорции.

b и с- средние члены пропорции.

• Пропорция – равенство двух отношений.

Деление можно заменить чертой дроби.

• Основное свойство пропорции:

3,6 = 6,3

1,2 2,1

• Читают : « Отношение a к b равно отношению c к d или a так относится к b ,как c относится к d ».
• В записи это первый и последний член.
• Крайние члены : 3,6 и 2, 1

Средние члены :1,2 и 6,3

В верной пропорции произведение крайних членов равно произведению средних.

Прямая и обратная пропорциональность.

Зависимость прямо пропорциональная

Две величины называют прямо пропорциональными,

если при увеличении ( уменьшении) одной из них в несколько раз другая увеличивается (уменьшается ) во столько же раз.

Составляем пропорцию ( следуем по «стрелкам»)

Зависимость обратно пропорциональная.

Две величины называют обратно пропорциональными если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается ) во столько же раз.

Масштаб

Масштаб –

Задача 1

Масштаб 1: 1 000 000

это отношение двух отрезков:

длины на карте к длине отрезка на местности.

Пусть x см длина отрезка на местности.

Зависимость прямо пропорциональная.

Пусть x км длина отрезка на карте.

Зависимость прямо пропорциональная.

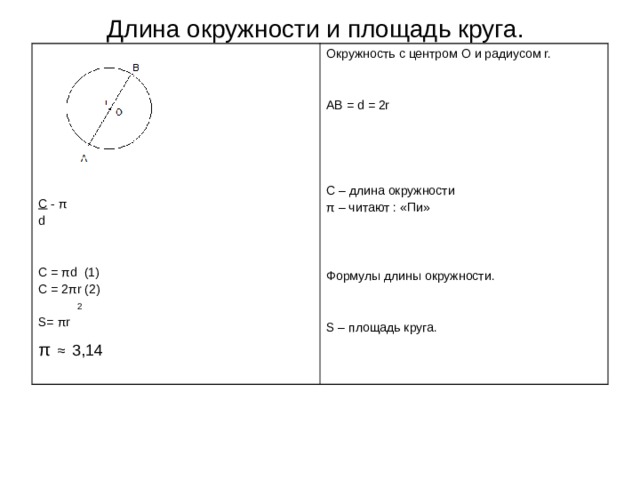
Длина окружности и площадь круга.

C - π

d

C = π d (1)

C = 2 π r (2)

2

S= π r

π ≈ 3,14

Окружность с центром O и радиусом r.

AB = d = 2r

C – длина окружности

π – читают : «Пи»

Формулы длины окружности.

S – площадь круга.

Координаты на прямой.

A (1)

B ( - 2)

C ( 3)

Координатная прямая, на которой :

1) Точка O – начало отсчёта ( начало координат)

Читают: «Точка A с координатой 1»

• Выбрано положительное направление.

• Выбран единичный отрезок.

Координата точки- это число, показывающее положение точки на прямой.

Противоположные числа.

A ( 2)

B (-2)

2 и -2 – противоположные числа.

Для каждого числа есть одно противоположное.

0 противоположен сам себе.

• a – читают: « Число противоположное a ».

2 и -2 удалены от 0 на одинаковое расстояние, вправо и влево.

Противоположные числа- это числа, которые отличаются только знаком.

Целые числа – это натуральные числа, противоположные им отрицательные числа и нуль.

0; |-a| = a, если a |-a| = |a| OA= (4) OB= (2) Модуль -4 равен 4. Модуль 2 равен 2 . Модулем числа a называется расстояние O (o) до A (a). Модули противоположных чисел равны. " width="640"

Модуль числа

|-4| = 4

|2| = 2.

|0| = 0

|a| = a, если a 0;

|-a| = a, если a

|-a| = |a|

OA= (4)

OB= (2)

Модуль -4 равен 4.

Модуль 2 равен 2 .

Модулем числа a называется расстояние

O (o) до A (a).

Модули противоположных чисел равны.

0 ; 3 0 1 -2 6 1 - 1 - 2 , т. к любого отрицательного. |-1| 1 Из двух положительных чисел, больше то, модуль которого больше. Из двух отрицательных чисел больше то, модуль которого меньше. " width="640"

Сравнение чисел.

O (0)

A (2)

B (3)

C (-2)

D (-1)

• -1

• На координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.
• Любое отрицательное число меньше нуля.
• Любое положительное число больше нуля.

• Любое положительное число больше

• 2 0 ; 3 0
• 1 -2
• 6 1
• - 1 - 2 , т. к

любого отрицательного.

|-1|

1

• Из двух положительных чисел, больше то, модуль которого больше.
• Из двух отрицательных чисел больше то, модуль которого меньше.

Изменение величин .

B (1)

D (3)

C (-1)

1 + 2 = 3

1 + ( -2) = -1

• Перемещение вправо обозначается положительным числом.
• Перемещение влево обозначается отрицательным числом.
• Увеличение любой величины- положительное число.
• Уменьшение любой величины – отрицательное число.

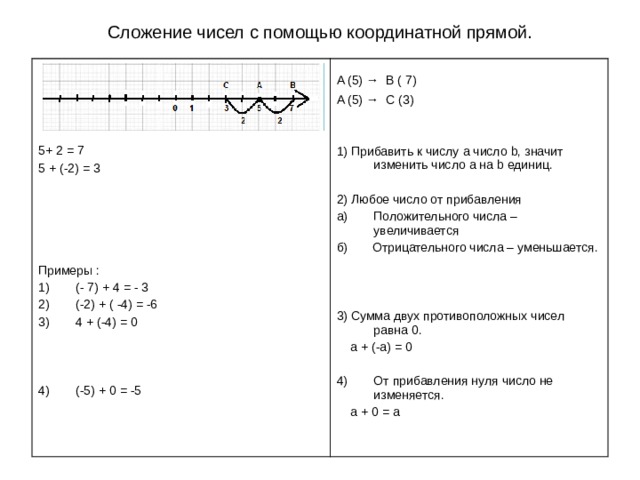
Сложение чисел с помощью координатной прямой.

5+ 2 = 7

5 + (-2) = 3

Примеры :

• (- 7) + 4 = - 3
• (-2) + ( -4) = -6
• 4 + (-4) = 0
• (-5) + 0 = -5

A (5) → B ( 7)

A (5) → C (3)

1) Прибавить к числу a число b , значит изменить число a на b единиц.

2) Любое число от прибавления

• Положительного числа – увеличивается

б) Отрицательного числа – уменьшается.

3) Сумма двух противоположных чисел равна 0 .

a + (-a) = 0

• От прибавления нуля число не изменяется.

a + 0 = a

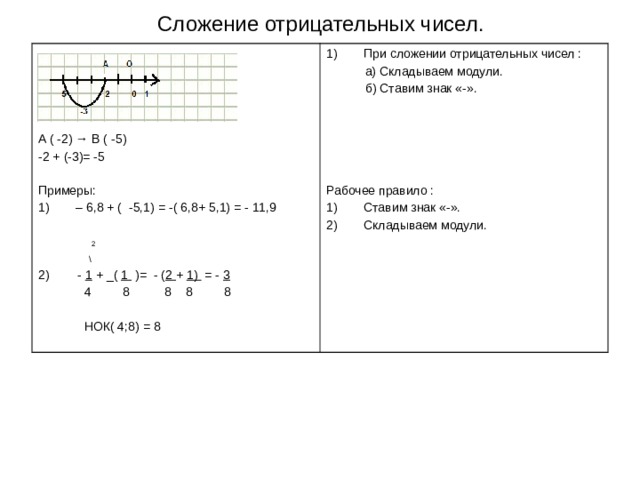
Сложение отрицательных чисел.

A ( -2) → B ( -5)

-2 + (-3)= -5

Примеры:

• – 6,8 + ( -5,1) = -( 6,8+ 5,1) = - 11,9

• При сложении отрицательных чисел :

2

\

2) - 1 + _( 1 )= - ( 2 + 1) = - 3

4 8 8 8 8

НОК( 4;8) = 8

a) Складываем модули.

б) Ставим знак «-».

Рабочее правило :

• Ставим знак «-».
• Складываем модули.

4 , 2 7 7 7 7 7 Ставим знак большего модуля. Из большего модуля вычитаем меньший. НОК ( 5; 3) = 15 2,7 + ( - 3,4 ) = - (3,4 – 2,7) = - 0,7 3 5 \ \ 4) - 8 4 + 2 1 = - ( 8 4 - 2 1 ) = 5 3 5 3 - ( 8 12 - 2 5 ) = - 6 7 15 15 15 " width="640"

Сложение чисел с разными знаками.

Примеры:

• 6,1 + (-4,2) = + ( 6,1 – 4,2) = 1,9

Рабочее правило :

• Сравниваем модули чисел, находим больший.

• - 3 2 + 4 5 = 4 5 - 3 2 = 1 3

| 6,1|= 6,1; |-4,2|= 4,2

6,1 4 , 2

7 7 7 7 7

• Ставим знак большего модуля.
• Из большего модуля вычитаем меньший.

НОК ( 5; 3) = 15

• 2,7 + ( - 3,4 ) = - (3,4 – 2,7) = - 0,7

3 5

\ \

4) - 8 4 + 2 1 = - ( 8 4 - 2 1 ) =

5 3 5 3

- ( 8 12 - 2 5 ) = - 6 7

15 15 15

Вычитание.

Пример :

5 – 13 = 5 + ( -13) = - (13 – 5) = - 8

Определение :

a - b = a + (- b )

Примеры :

• 8 – 15 = 8 + ( -15) = - (15 – 8) = - 7
• - 15 – 6 = - 15 + (-6) = - ( 15 + 6) = - 21
• - 6 – 15 = - 6 + ( -15) = - 21
• 10 - ( -5) = 10 + 5 = 15

Из числа a вычесть число b , значит к числу a прибавить число противоположное b .

Если уменьшаемое меньше вычитаемого, то разность отрицательна .

Для – 5 противоположно 5.

НОК ( 3 ; 2 ) = 6

2 3

\ \

• 1 - 1 = 2 - 3 = 2 + ( - 3 ) = - ( 3 - 2 )

3 2 6 6 6 6 6 6

= - 1

6

Расстояние между точками.

Дано :

A (-5), B (9)

Найти длину отрезка AB.

Решение:

AB = 9 – (-5) = 9 + 5= 14

Чтобы найти длину отрезка, надо :

Из координаты правого конца вычесть координату левого конца. ( У правого конца координата больше).

Умножение.

а) Произведение отрицательных чисел – положительное число.

б) Перемножаем модули.

При умножении чисел с разными знаками :

• Ставим знак «-».
• Перемножаем модули.

Деление.

Примеры :

• а) - 12 : (-4) = 12 : 4 = 3

б) - 5,4 : (- 0,9) = 5,4 : 0,9 = 54 : 9 = 6

в) - 5,4 : (- 6) = 5,4 : 6 = 0,9

3) 0 : (-6) = 0

• а) Частное отрицательных чисел – положительное число.

б) Модуль делимого разделить на модуль делителя.

Переносим запятую и в делимом, и в делителе на 1 знак вправо.

Если целая часть делимого меньше делителя,

то в частном будет 0 целых .

При делении чисел с разными знаками :

а) Ставим знак «-»

б) Модуль делимого разделить на модуль делителя.

2 1 = 7

3 3

При делении нуля на любое число, получается нуль.

На 0 делить нельзя !!!

Рациональные числа.

• a , где а – целое число, n – натуральное

n число.

• Рациональное число.

Любое число – рациональное число.

Любая дробь ( положительная, отрицательная, десятичная, смешанное число) – рациональное число.

Сумма

Разность

Произведение

Частное( если знаменатель – рациональное число), тоже являются рациональными числами.

Любое рациональное число можно представить в виде десятичной или периодической дроби.

• а = а

1

- 5 = -5 ; 7 = 7 ; 0 = 0

1 1 1

3 2

\ \

• 1 + 1 = 3 + 2 = 5

2 3 6 6 6

- 1 - 1 = - 2 – 3 = - 2 + ( - 3 ) = - 5

3 2 6 6 6 6 6

7 = 0,28

25

1 = 0,33… = 0,(3)

3

1 = 0,0666… = 0,0(6)

15

Свойства действий с рациональными числами.

1) a+b = b+a , a+(b+c)= (a+b)+c

2,6 + 7,3 = 7,3 + 2,6 = 9,9

3 + ( 5 + 9 ) = ( 3 + 5 ) + 9 = 1 9 = 2 1

8 8 8 8 8 8 8 8

2) a + 0 = a ;

a + (-a) = 0

- 5 + 0 = - 5 ; 7,9 + ( - 7,9) = 0

6 6

1) Сложение обладает переместительным и

сочетательным свойствами.

8 = 1

8

2) а) От прибавления нуля число не изменяется.

б) Сумма противоположных чисел равна 0.

3) Умножение обладает переместительным и сочетательным свойствами.

4) Умножение на 1 не изменяет число, произведение взаимно обратных чисел = 1.

5) При умножении на : а) Нуль получается 0.

б) Произведение равно 0, когда хотя бы один

из множителей равен 0.

Свойства действий с рациональными числами.( продолжение)

Распределительное свойство умножения относительно сложения.

Раскрытие скобок.

• Перед скобками стоит знак «+».

- 2,87 + ( 2,87 – 7,639) =

0

- 2,87 + 2,87 - 7,639 = - 7,639

• Опускаем скобки ( не пишем) и знак «+», и все слагаемые записываем с их знаками.
• Опускаем скобки и знак «-», и все слагаемые записываем с противоположными знаками.
• Раскрываем скобки и используем переместительный и сочетательный

• Перед скобками стоит знак «-».

законы сложения.

9,36 - (9,36 – 5,48) =

0

9,36 – 9,36 + 5,48 = 5,48

• ( - 4 – 20 ) + (6 + 13) – (7-8) – 5 =

- 4 – 20 + 6 + 13 -7 +8 – 5 = - ( 4+ 20+ 7

+ 5) = - 36 + ( 6 + 13 + 8)= - 36 + 27= - 9

Коэффициент.

• Числовой множитель -0,21 – это коэффициент (обычно пишем на 1-ом месте).
• Коэффициент а) 1

б) 1

в) – 1

Упростим выражение

Коэффициент- 8

Подобные слагаемые.

1) ( a + b)c = ac + bc

Примеры :

Раскрытие скобок с применением распределительного

свойства умножения.

• - 3 умножим на a.

-3 умножим на (-2 b)

2) а) Слагаемые с одинаковыми буквенными

множителями называют подобными слагаемыми .

б) Упростить выражения можно только с подобными

слагаемыми.Эти упрощения называются приведением

подобных слагаемых.

3) Для упрощения выполним действия

над коэффициентами.

3- 5= -2

4) Две группы подобных слагаемых.

1) -6-1= -7

2) 8 – 1= 7

Решение уравнений.

• 4( x + 5) = 12

4(x+ 5) = 12

4 4

(x+5)= 3

x= 3-5

Ответ: x = - 2.

Примеры :

3 3 3

1 x + 12 = x

3

x+ 36 = 3x

x – 3x= -36

- 2x = -36

x = 36 : 2

x = 18

Ответ : x = 18

x +7 = 2x-3

3 5

5( x+ 7) = 3(2x-3)

5x + 35 = 6x – 9

5x – 6x = -9 – 35

-1x = - 44

x – 44 : 1

x = 44

Ответ : x = 44

• Разделим обе части уравнения на 4 ( или умножим на 1)

4

2) Слагаемые переносим из одной части в другую, изменив знак на противоположный.

• Умножим обе части уравнения на 3.

12 = 12 ; x = x

1 1

• Переносим слагаемые из одной части в другую

( с переменной влево, без переменной вправо)

• Приводим подобные слагаемые

x = 1x

1x- 3x = - 2x

• По основному свойству пропорции:

произведение крайних членов равно произведению средних

• 5x + 35

6 x - 9

3) См. предыдущий пример.

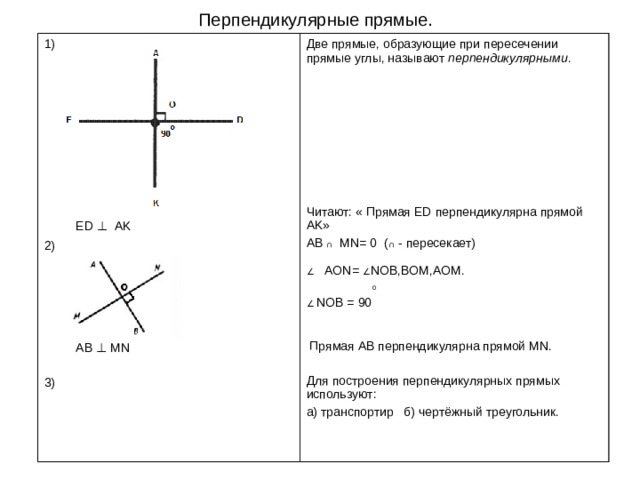
Перпендикулярные прямые.

1)

ED ⊥ AK

2)

AB ⊥ MN

3)

Две прямые, образующие при пересечении прямые углы, называют перпендикулярными .

Читают: « Прямая ED перпендикулярна прямой AK »

AB ∩ MN= 0 ( ∩ - пересекает)

∠   AON= ∠ NOB,BOM,AOM.

о

∠ NOB = 90

Прямая AB перпендикулярна прямой MN.

Для построения перпендикулярных прямых используют:

а) транспортир б) чертёжный треугольник.

Параллельные прямые.

1) AB || CD

2)

3)

AC m AC || BD

BD m

Прямые, которые не пересекаются, называются параллельными.

Построим через точку A , прямую, параллельную прямой a .

b || a

Координатная плоскость.

M ( 3 ; -5)

3 - абсцисса

- 5 - ордината

E ( -1 ; 4)

S ( 2 ; 0 )

Система координат.

Точка O – начало координат.

xOy – координатная плоскость.

Ox – ось абсцисс.

Oy – ось ординат.

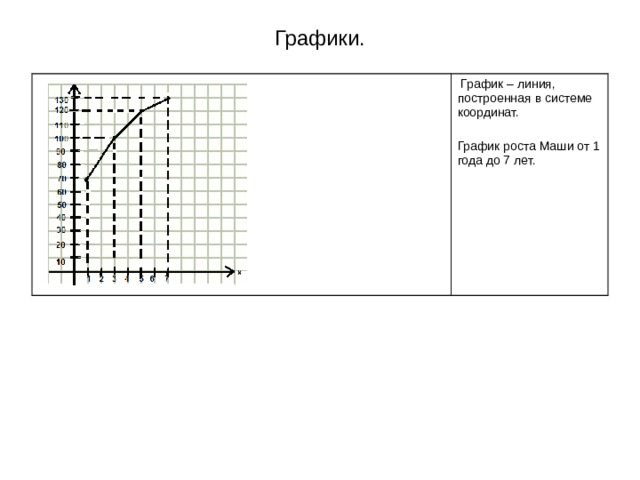
Графики.

График – линия, построенная в системе координат.

График роста Маши от 1 года до 7 лет.