13
Министерство образования, науки и молодёжной политики
Краснодарского края
государственное бюджетное профессиональное образовательное учреждение
Краснодарского края «Краснодарский педагогический колледж»

УЧЕБНЫЙ ПРОЕКТ
по дисциплине ОУД.03 Математика: алгебра и начала математического анализа; геометрия
КОМПЛЕКСНЫЕ ЧИСЛА
специальность Преподавание в начальных классах
Выполнили:
студентки 1 курса группы «Аш»
школьного отделения
Колтунова Дарья Евгеньевна
Лаптева Виктория Александровна
Преподаватель:
Степанян Л. У.
Краснодар, 2017 г.
СОДЕРЖАНИЕ
Введение……………………………………………………………… 3
I. История возникновения комплексных чисел…………………...3-4
II. Комплексные числа и их свойства……………………………..5-6
Понятие комплексного числа
Геометрическое изображение комплексных чисел
Тригонометрическая форма комплексного числа
III. Действия с комплексными числами…………………………..6-8
сложение
вычитание
умножение
деление
IV. Решение уравнений с комплексными числами……………....8-9
VI. Заключение……………………………………………………...10
VII. Список литературы………………………………………….…11
Введение
История развития числа уходит своими корнями в далекое прошлое. И на заре цивилизации числа возникли из практических потребностей людей в счете. По мере развития общества развивалось и понятие о числе. Многим может показаться, что о числах уже все изучено в древности. До недавнего времени и я так считал, но узнав о существовании комплексных чисел, позволяющих, главным образом, совершить такую операцию как извлечение корня из отрицательного числа, я был достаточно сильно удивлен. Я изменил свое мнение о том, что развитие числа прекратилось.
Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами. Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 - 1921) при разработке теории крыла, автором которой он является. Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники. Сейчас комплексные числа активно применяются в информатике, динамике, электромеханике, радиотехнике, алгебре векторов , теории упругости, активно развиваются в других науках.
Цель настоящего реферата знакомство с историей появления комплексных чисел, их свойствами, действиями над ними, а также с решением уравнений с комплексным переменным.
I. История возникновения комплексных чисел
Древние греки использовали числа для подсчета предметов, поэтому действительными, настоящими они признавали только натуральные числа. Позже на ряду с натуральными числами стали применять дроби-числа, составленные из целого числа долей единицы(рациональные). В практических расчетах дроби применяли в III веке до н. э. в древнем Египте и древнем Вавилоне.
Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби. Древнегреческий философ и математик Пифагор учил, что "... элементы чисел являются элементами всех вещей и весь мир в целом является гармонией и числом. Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с этого открытия начинается эра теоретической математики: открыть существование несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению, было невозможно.
Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел - это было сделано китайскими математиками за два века до н. э. Отрицательные числа применяли в III веке древнегреческий математик Диофант и в VII веке эти числа уже подробно изучили индийские ученые. Уже в VIII веке было установлено, что квадратный корень из положительного числа имеет два значения - положительное и отрицательное, а из отрицательных чисел квадратный корень извлекать нельзя
В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. формула решения кубических уравнений вида 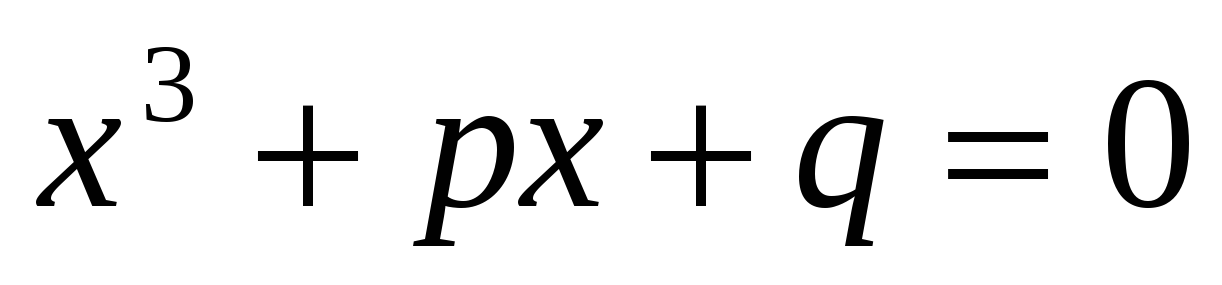 безотказно действует в случае, когда уравнение имеет один действительный корень (
безотказно действует в случае, когда уравнение имеет один действительный корень (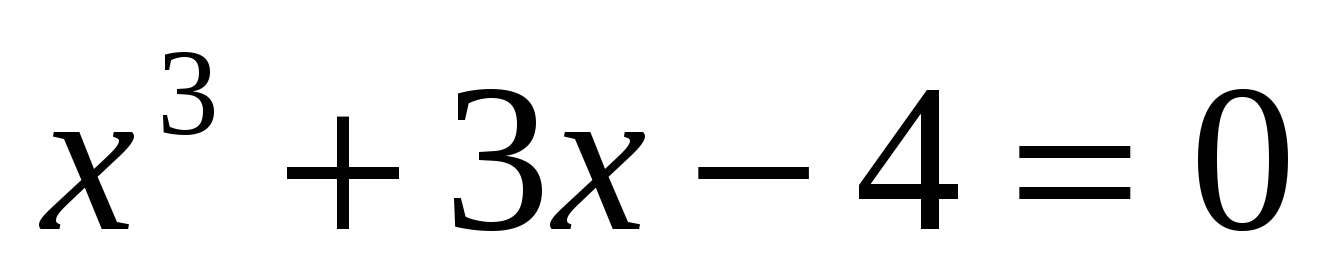 ), а если оно имеет три действительных корня (
), а если оно имеет три действительных корня (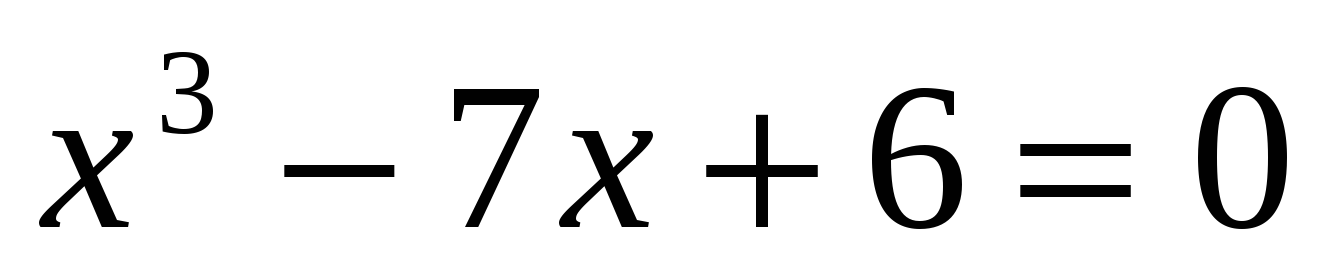 ), то под знаком квадратного корня оказывалось отрицательное число. Именно из-за этого противоречия появился термин “мнимое число, мнимая часть”, а за ним и само “комплексное число”. Всегда ли разумны запреты? Представим, что некоторые задачи весьма успешно решаются только с нарушением определённого правила, и никак не удаётся найти “законного” способа их решения. Не стоит ли в таком случае отказаться от ограничения, ставшего слишком обременительным?
), то под знаком квадратного корня оказывалось отрицательное число. Именно из-за этого противоречия появился термин “мнимое число, мнимая часть”, а за ним и само “комплексное число”. Всегда ли разумны запреты? Представим, что некоторые задачи весьма успешно решаются только с нарушением определённого правила, и никак не удаётся найти “законного” способа их решения. Не стоит ли в таком случае отказаться от ограничения, ставшего слишком обременительным?
Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что система уравнений 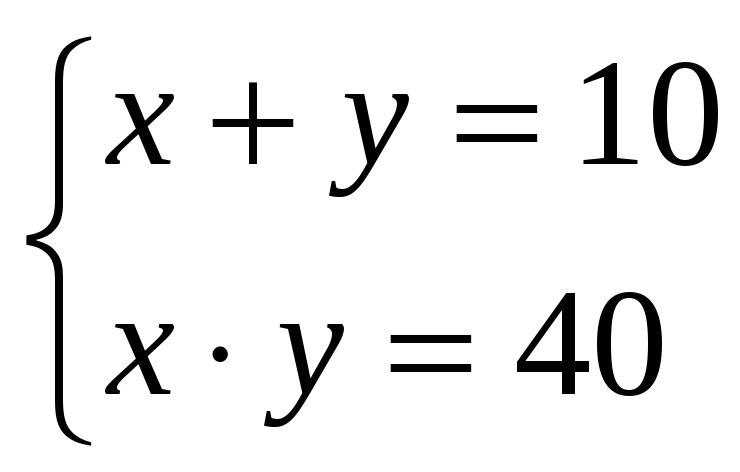 , не имеющая решений во множестве действительных чисел, имеет решения вида
, не имеющая решений во множестве действительных чисел, имеет решения вида 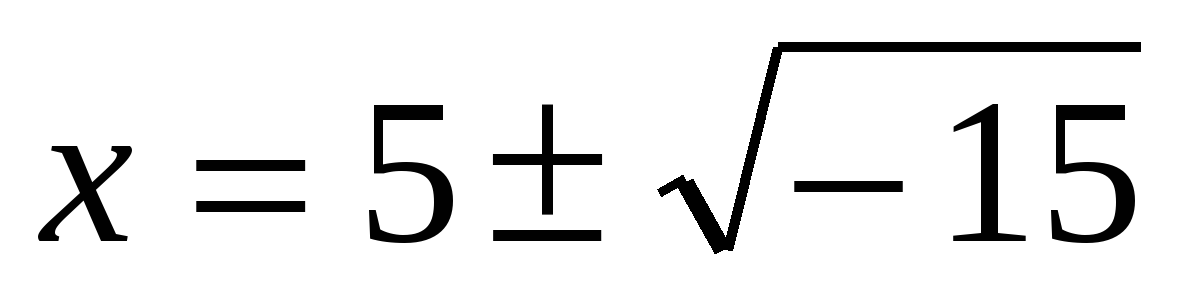 ,
, 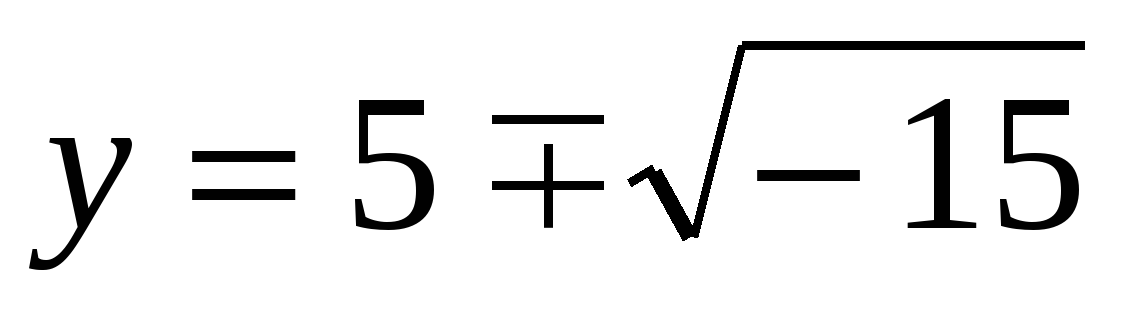 , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что
, нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что 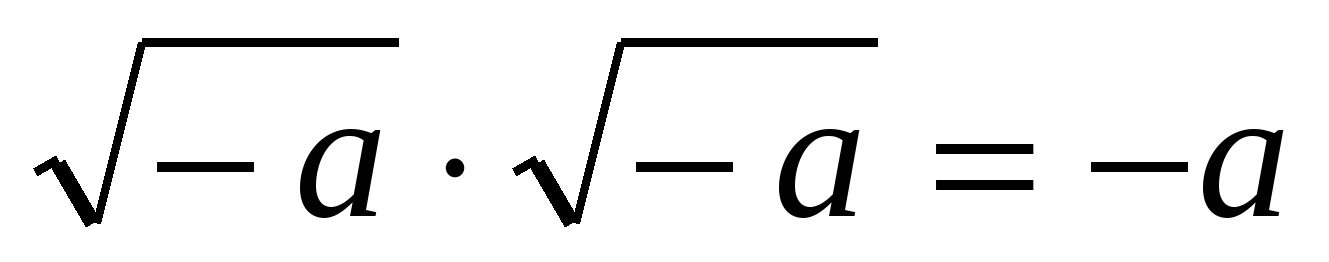 . Кардано называл такие величины “чисто отрицательными” и даже “софистически отрицательными”, считал их бесполезными и старался их не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа
. Кардано называл такие величины “чисто отрицательными” и даже “софистически отрицательными”, считал их бесполезными и старался их не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа 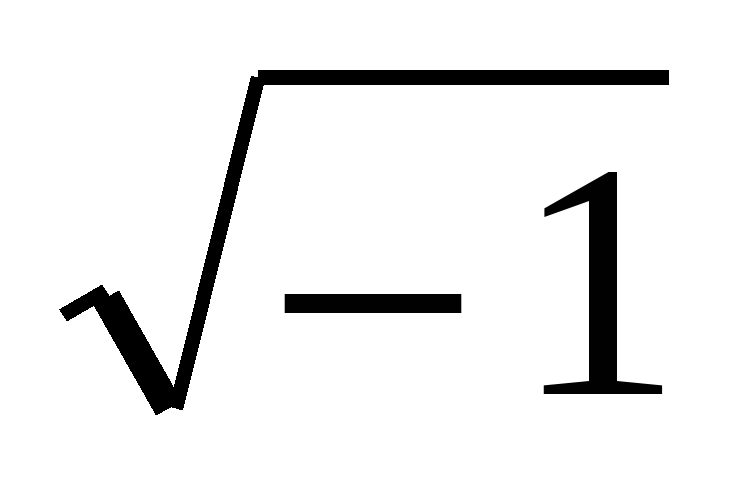 (мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. Образующих единое целое.
(мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. Образующих единое целое.
II. Комплексные числа и их свойства
Комплексными числами называются выражения вида z = a + ib, где a и b – любые действительные числа, а i – мнимая единица, основное свойство которой i2= -1. Множество комплексных чисел обозначается С. Комплексные числа должны рассматриваться не в отрыве от действительных, а совместно с ними. Поэтому множество действительных чисел R входят во множество С, и всякое действительное число обозначается как z = a  0i. Пример: запись 3+0i то же, что и 3; запись -4+0i значит то же, что -4.
0i. Пример: запись 3+0i то же, что и 3; запись -4+0i значит то же, что -4.
А числа вида z = 0 +ib называют чисто мнимыми и обозначаются ib. Они получаются из комплексных чисел при a = 0.
Геометрическое изображение комплексных чисел
Действительные числа можно изобразить точками прямой линии/
Каждая точка С "числовой прямой" изображает некоторое действительное число (рациональное, если отрезок ОС соизмерим с единицей длины, и иррациональное, если несоизмерим). Таким образом, на "числовой прямой" не остаётся места для комплексных чисел.
Но комплексные числа можно изобразить на "числовой прямой". Для этого мы выбираем на плоскости прямоугольную систему координат с одним и тем же масштабом на обеих осях (рис. 1). Комплексное число a + bi мы изображаем точкой М, у которой абсцисса х равна абсциссе а комплексного, а ордината у равна ординате b комплексного числа.
М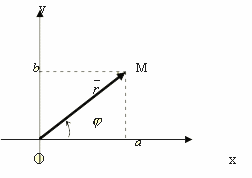 одулем комплексного числа z = a +ib называется длина вектора, соответствующего этому числу; |z| = r =
одулем комплексного числа z = a +ib называется длина вектора, соответствующего этому числу; |z| = r = 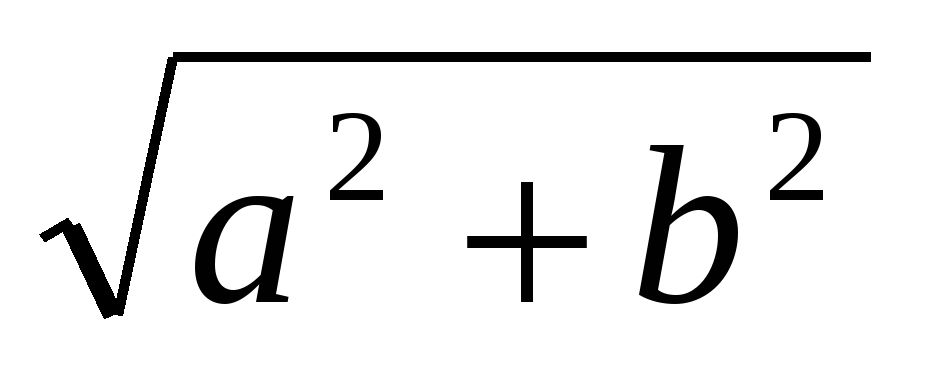 . Аргументом комплексного числа Z
. Аргументом комплексного числа Z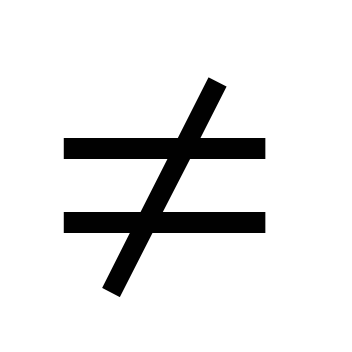 0 называется величина угла
0 называется величина угла  между положительным направлением действительной оси и вектором Z (r).
между положительным направлением действительной оси и вектором Z (r). 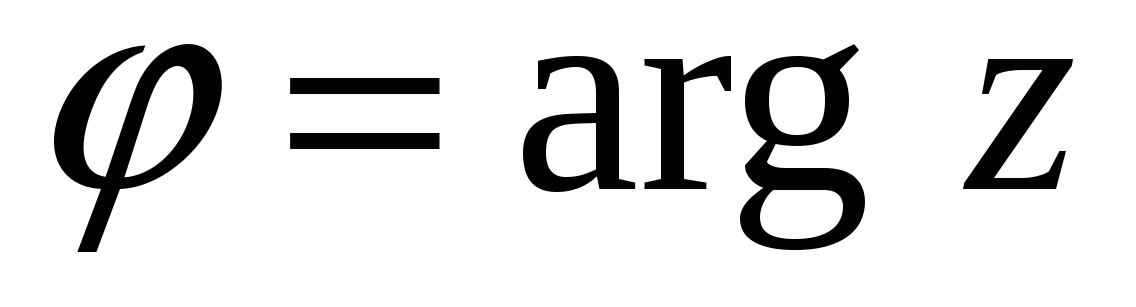 ; Аrg z = j + 2πκ;
; Аrg z = j + 2πκ;
Если Cos j = а / 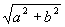 = а / r;
= а / r;
Sin j = b / 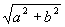 = b / r;
= b / r;
то воспользовавшись связью a = rcos , b = rsin
, b = rsin , получим тригонометрическую форму записи числа: z = r(cos
, получим тригонометрическую форму записи числа: z = r(cos + i sin
+ i sin ).
).
Сегодня сложно себе представить ряд наук, обходящихся без применения комплексных чисел. Такие области, как вышеуказанное самолётостроение и радиотехника, электротехника и электромеханика, компьютерное программирование и экономика невозможны без применения моделей в виде комплексных чисел. Комплексные числа, несмотря на их “лживость” и недействительность, имеют очень широкое применение. Они играют значительную роль не только в математике, а также в таких науках, как физика, химия. В настоящее время комплексные числа активно используются в электромеханике, компьютерной и космической индустрии. К сожалению, их периодически исключают из школьной программы, а это один из красивейших разделов математики.
Комплексные числа сами по себе являются мощным инструментом в решении многих математических задач, справиться с которыми посредством действительных чисел слишком сложно.
В настоящее время на путях обобщения понятия числа пришли к понятию гиперкомплексных чисел. Понятие гиперкомплексного числа шире, чем понятие комплексных чисел. Простейшим примером гиперкомплексных чисел являются кватернионы, которые дали толчок развитию алгебры векторов, применяемой в современной физике и технике, в частности, в теории электричества и электротехники, в динамике, аэродинамике и теории упругости.
Комплексные числа – очень интересный предмет для изучения, дающий ключ к решению многих задач, не поддающихся рассмотрению в узких границах элементарной математики.
III. Действия с комплексными числами
1. Сложение комплексных чисел
Определение: Суммой комплексных чисел a + bi и a' + b'i называют комплексное число (a + a') + (b + b')i.
Это определение подсказывается правилами действий с обычными многочленами.
Пример 1. (-3 + 5i) + (4 - 8i) = 1 - 3i
Пример 2. (2 + 0i) + (7 + 0i) = 9 + 0i. Так как запись 2 + 0i означает то же, что и 2 и т. д., то наполненное действие согласуется с обычной арифметикой (2 + 7=9).
Пример 3. (0 + 2i) + (0 + 5i) = 0 + 7i, т. е. 2i + 5i = 7i
Пример 4. (-2 + 3i) + ( - 2 - 3i) = - 4
В примере 4 сумма двух комплексных чисел равна действительному числу. Два комплексных числа a+bi и a-bi называются сопряженными. Сумма сопряженных комплексных чисел равна действительному числу.
Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
2. Вычитание комплексных чисел.
Определение. Разностью комплексных чисел a + bi (уменьшаемое) и a' + b'i (вычитаемое) называется комплексное число (a - a') + (b - b')i.
Пример 1. (-5 + 2i) - (3 - 5i) = -8 + 7i
Пример 2. (3 + 2i) - (-3 + 2i) = 6 + 0i = 6
3. Умножение комплексных чисел.
Определение. Произведением комплексных чисел a + bi и a' + b'i называется комплексное число
(aa' - bb') + (ab' + ba')i.
Замечание. На практике нет нужды пользоваться формулой произведения. Можно перемножить данные числа, как двучлены, а затем положить, что i2 = -1.
Пример 1. (1 - 2i)(3 + 2i) = 3 - 6i + 2i - 4i 2 = 3 - 6i + 2i + 4 = 7 - 4i.
Пример 2. (a + bi)(a - bi) = a2 + b 2
Пример 2 показывает, что произведение сопряженных комплексных чисел есть действительное и притом положительное число.
Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.
4. Деление комплексных чисел.
В соответствии с определением деления действительных чисел устанавливается следующее определение.
Определение. Разделить комплексное число a + bi на комплексное число a' + b'i - значит найти такое число x + yi, которое, будучи помножено на делитель, даст делимое.
Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем: (a + bi):(c + di)=
Пример 1. Найти частное (7 - 4i):(3 + 2i).
Записав дробь (7 - 4i)/(3 + 2i), расширяем её на число 3 - 2i, сопряженное с 3 + 2i. Получим:
((7 - 4i)(3 - 2i))/((3 + 2i)(3 - 2i)) = (13 - 26i)/13 = 1 - 2i.
Пример 1 предыдущего пункта даёт проверку.
Пример 2. (-2 +5i)/(-3 -4i) = ((-2 + 5i)(-3 - 4i))/((-3 - 4i)( -3 + 4i)) = (-14 -23i)/25 = -0,56 - 0.92i.
Чтобы доказать, что правая часть действительно является частным, достаточно помножить её на a' + b'. Получим a + bi.
IV. Решение уравнений с комплексными переменными
Рассмотрим сначала простейшее квадратное уравнение z2 = a, где а - заданное число, z - неизвестное. На множестве действительных чисел это уравнение:
1) имеет один корень z = 0, если а = 0;
2) имеет два действительных корня z1,2 = , если а0;
3) не имеет действительных корней, если а
На множестве комплексных чисел это уравнение всегда имеет корень .
Задача 1. Найти комплексные корни уравнения z2 = a, если:
1) а = -1; 2) а = -25; 3) а = -3.
1) z2 = -1. Так как i2 = -1, то это уравнение можно записать в виде z2 = i2, или z2 - i2 = 0. Отсюда, раскладывая левую часть на множители, получаем (z-i)(z+i) = 0, z1 = i, z2 = -i.Ответ. z1,2 = i.
2) z2 = -25. Учитывая, что i2 = -1,преобразуем это уравнение:
z2 = (-1)25,
z2 = i2 52, z2 - 52 i2= 0, (z-5i)(z+5i) = 0, откуда z1 = 5i, z2 = -5i.Ответ:
z 1,2 = 5i.
3) z2 = -3, z2 = i2()2, z2 - ()2i2 = 0, (z - i)(z + i) = 0
Ответ: z1,2 = i.
Вообще уравнение z2 = a, где а
Используя равенство i2 = -1, квадратные корни из отрицательных чисел принято записывать так: = i, = 2i, = i .
Итак, определен для любого действительного числа а (положительного, отрицательного и нуля). Поэтому любое квадратное уравнение az2 + bz + c = 0, где а, b, с - действительные числа, а 0, имеет корни. Эти корни находятся по известной формуле:
Z1,2 = .
Задача 2. Решить уравнение z2-4z+13=0. По формуле находим: z1,2 = = = 2 3i.
Заметим, что найденные в этой задаче корни являются сопряженными: z1=2+3i и z2=2-3i. Найдем сумму и произведение этих корней: z1+z2=(2+3i)+(2-3i)=4, z1z2=(2+3i)(2-3i)=13.
Число 4 - это 2-й коэффициент уравнения z2-4z+13=0, взятый с противоположным знаком, а число 13- свободный член, то есть в этом случае справедлива теорема Виета. Она справедлива для любого квадратного уравнения: если z1 и z2 - корни уравнения az2+bz+c = 0, z1+z2 = , z1z2 = .
Задача 3. Составить приведенное квадратное уравнение с действительными коэффициентами, имеющие корень z1=-1-2i.
Второй корень z2 уравнения является числом, сопряженным с данным корнем z1, то есть z2=-1+2i. По теореме Виета находим
P=-(z1+z2)=2, q=z1z2=5. Ответ z2-2z+5=0.
V. Заключение
Мы старались в своей работе проанализировать, как с развитием общества и науки развивается понятие числа. На сегодняшний день наибольшим множеством чисел являются комплексные и гиперкомплексные числа. Но и на этом множестве невозможно выполнение операции деления на нуль. Может быть с дальнейшим развитием нашего общества и науки и этот последний запрет будет снят. Ведь не зря же Математика – Царица всех наук и находится в постоянном развитии.
VI. Список литературы
А.П. Савин "Энциклопедический словарь юного математика"
М.Я. Выгодский "Справочник по элементарной математике"
И.С. Петраков "Математические кружки в 8-10 классах"
М.И. Сканави "Сборник задач по математике (геометрия)"
arbuz.uz
Referat.ru
Students.ru
wikipedia.org
5ballov.ru
13






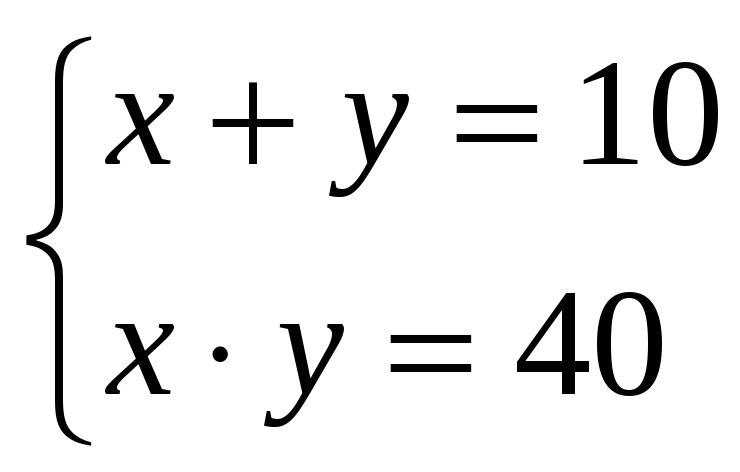 , не имеющая решений во множестве действительных чисел, имеет решения вида
, не имеющая решений во множестве действительных чисел, имеет решения вида  одулем комплексного числа z = a +ib называется длина вектора, соответствующего этому числу; |z| = r =
одулем комплексного числа z = a +ib называется длина вектора, соответствующего этому числу; |z| = r = 

















