ТЕМА УРОКА .ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ,
ЕГО ОСНОВНЫЕ СВОЙСТВА. Формула Ньютона-Лейбница.
1. Задачи, приводящие к понятию определённого интеграла
Задача о площади криволинейной трапеции.
Пусть на отрезке  определена непрерывная и неотрицательная функция
определена непрерывная и неотрицательная функция  .
.
Определение. Криволинейной трапецией называется часть плоскости, ограниченная графиком функции  , осью Ох (
, осью Ох ( ) и отрезками прямых
) и отрезками прямых  ,
,  .
.
П усть требуется найти площадь криволинейной трапеции.
усть требуется найти площадь криволинейной трапеции.
Для этого разобьём отрезок  точками
точками  на n частичных отрезков и положим
на n частичных отрезков и положим  ,
,  . Наибольшую из этих разностей обозначим через
. Наибольшую из этих разностей обозначим через  :
:  . На каждом частичном отрезке
. На каждом частичном отрезке  выберем произвольную точку
выберем произвольную точку  :
:  . Произведение
. Произведение  даст площадь прямоугольника с основанием
даст площадь прямоугольника с основанием  и высотой
и высотой  , тогда приближённо площадь
, тогда приближённо площадь  криволинейной трапеции
криволинейной трапеции  равна сумме:
равна сумме:
 ,
,  .
.
Эта сумма называется интегральной суммой.
Если увеличить количество частичных отрезков так, что длина любого из них будет стремиться к нулю, то данная интегральная сумма будет стремиться к площади  криволинейной трапеции:
криволинейной трапеции:
 ,
,  . (1)
. (1)
2. Свойства определённого интеграла
Рассмотрим основные свойства определенного интеграла, считая подынтегральную функцию  интегрируемой на отрезке
интегрируемой на отрезке  .
.
1. При перестановке пределов интегрирования знак определённого интеграла изменяется:
 .
.
2. Определённый интеграл от функции с равными пределами интегрирования равен нулю:
 .
.
3. Постоянный множитель можно вынести за знак определённого интеграла:
 ,
,  .
.
4. Определённый интеграл от алгебраической суммы двух функций равен алгебраической сумме определённых интегралов от этих функций:
 .
.
5. Определённый интеграл по отрезку равен сумме определённых интегралов по его частям:
 , где
, где  .
.
6. Если функция  - чётная на отрезке
- чётная на отрезке  , то выполняется равенство
, то выполняется равенство
 .
.
7. Если функция  - нечётная на отрезке
- нечётная на отрезке  , то выполняется равенство
, то выполняется равенство
 .
.
4. Вычисление определенного интеграла
Теорема. Если функция  интегрируема на отрезке
интегрируема на отрезке  и
и  – первообразная функции
– первообразная функции  на этом отрезке, то имеет место формула Ньютона–Лейбница:
на этом отрезке, то имеет место формула Ньютона–Лейбница:
 .
.
Эта формула позволяет вычислить определённый интеграл, зная какую-либо первообразную для интегрируемой функции. Первообразную для функции  можно найти, вычисляя неопределённый интеграл от этой функции.
можно найти, вычисляя неопределённый интеграл от этой функции.
Замечание.
Для краткости записи употребляется обозначение  .
.
ПРИМЕРЫ.
1)  .
.
2)  .
.
Вычислить определенный интеграл

Решение:

Пример 4: Решение:
 .
.
Домашнее Задание. Пример
Вычислить определенный интеграл

Просмотр содержимого документа
«ТЕМА УРОКА .ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ, ЕГО ОСНОВНЫЕ СВОЙСТВА. Формула Ньютона-Лейбница.»
ТЕМА УРОКА .ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ,
ЕГО ОСНОВНЫЕ СВОЙСТВА. Формула Ньютона-Лейбница.
1. Задачи, приводящие к понятию определённого интеграла
Задача о площади криволинейной трапеции.
Пусть на отрезке 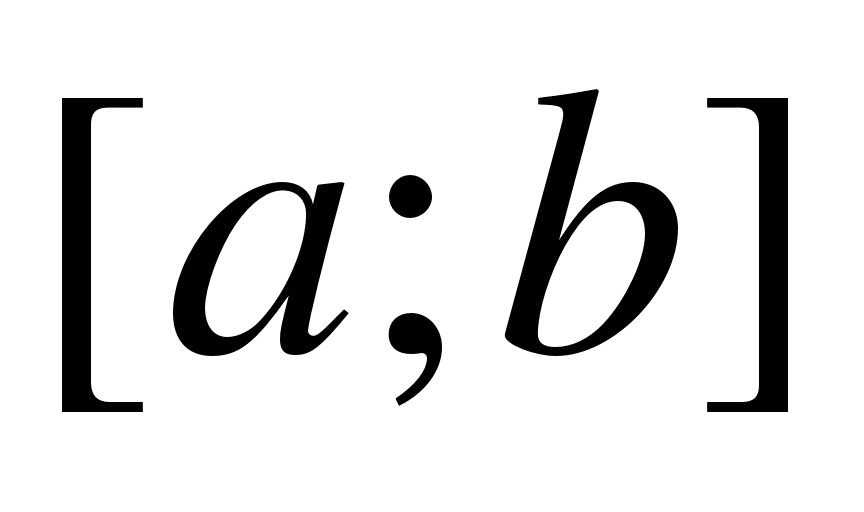 определена непрерывная и неотрицательная функция
определена непрерывная и неотрицательная функция 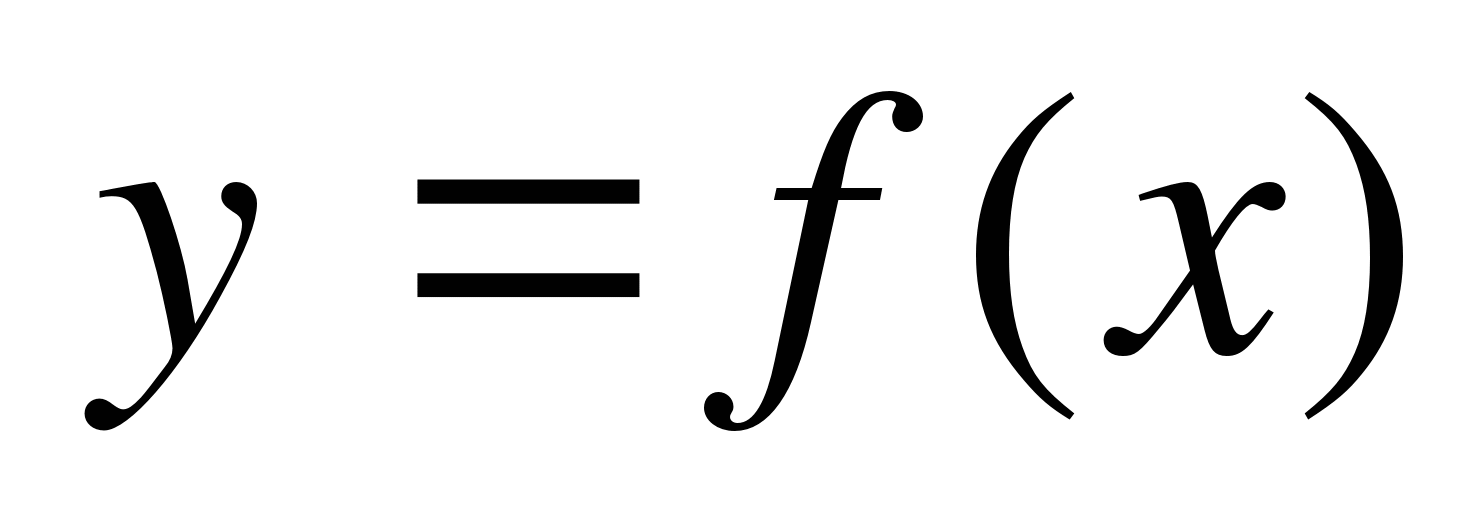 .
.
Определение. Криволинейной трапецией называется часть плоскости, ограниченная графиком функции 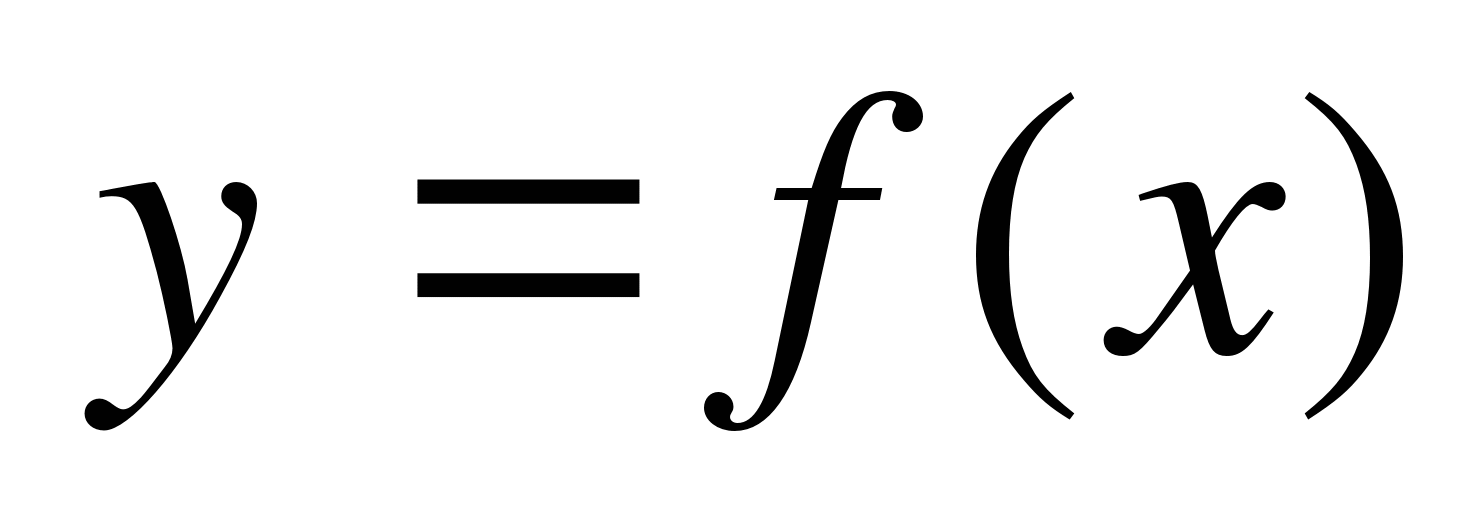 , осью Ох (
, осью Ох (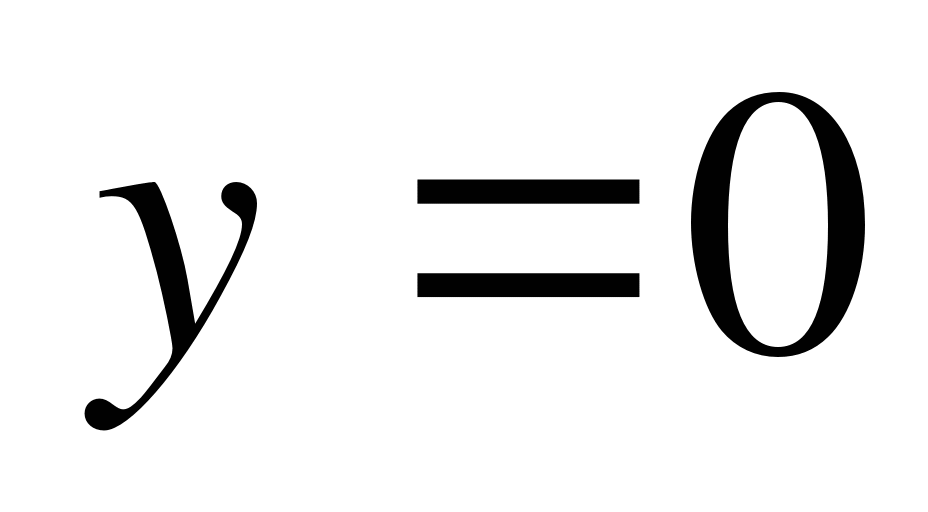 ) и отрезками прямых
) и отрезками прямых 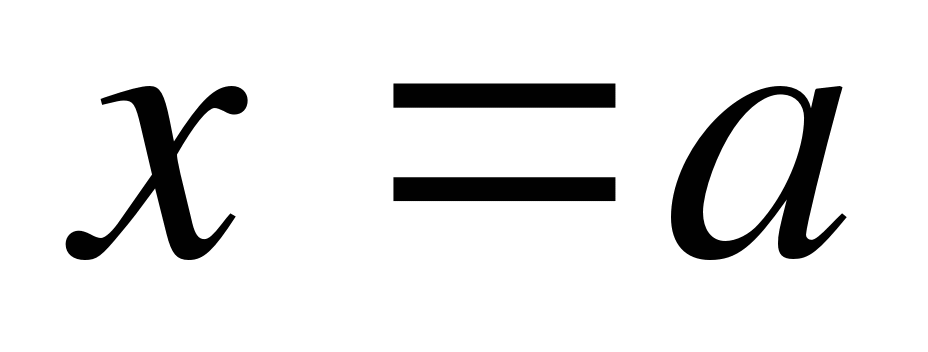 ,
, 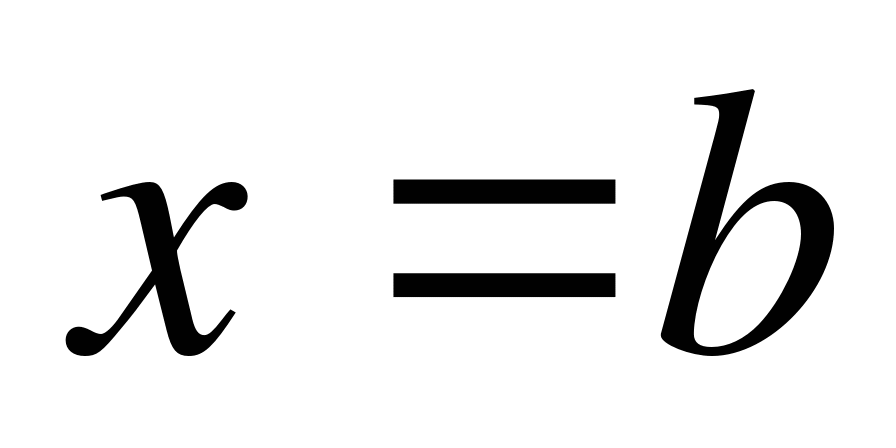 .
.
Пу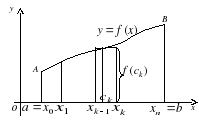 сть требуется найти площадь криволинейной трапеции.
сть требуется найти площадь криволинейной трапеции.
Для этого разобьём отрезок 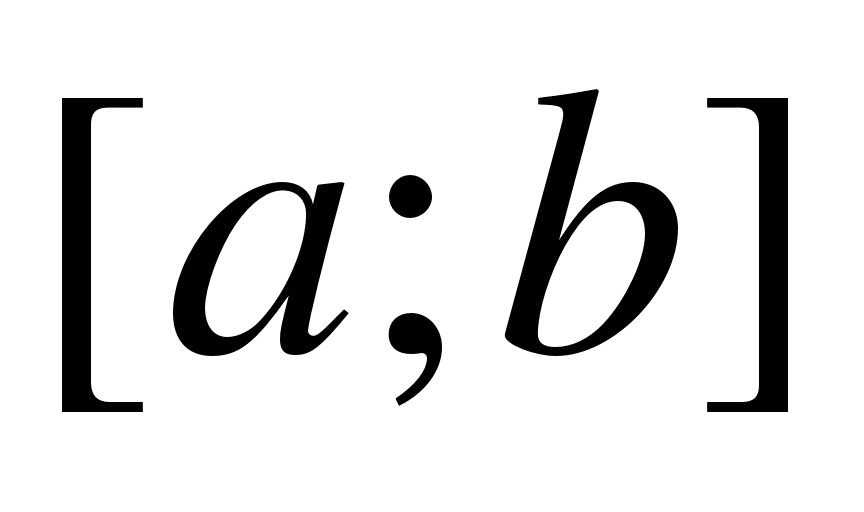 точками
точками 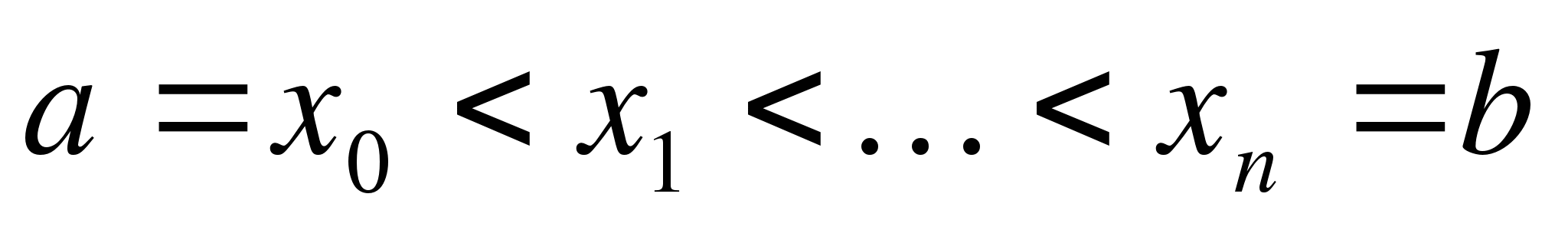 на n частичных отрезков и положим
на n частичных отрезков и положим 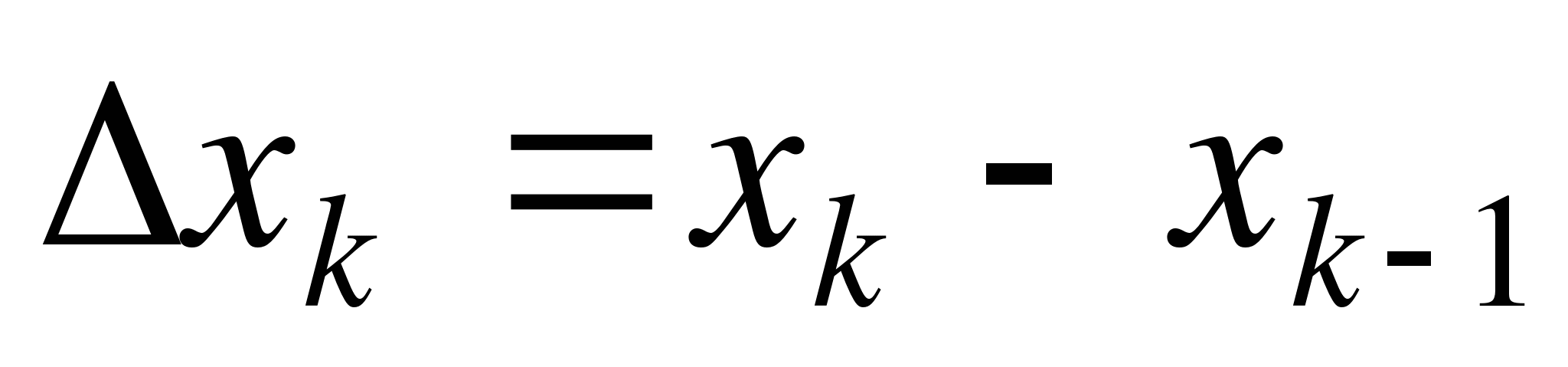 ,
, 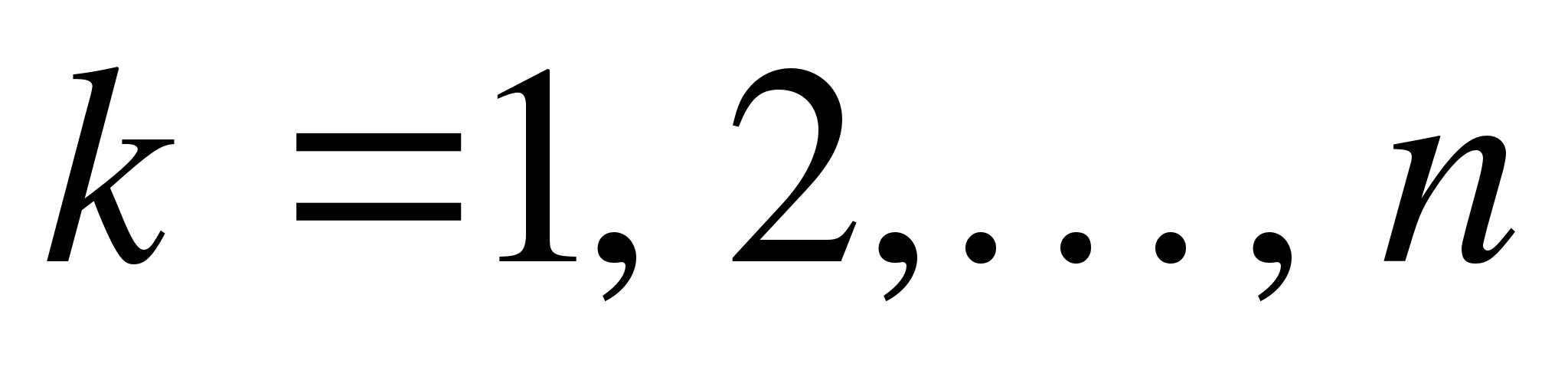 . Наибольшую из этих разностей обозначим через
. Наибольшую из этих разностей обозначим через 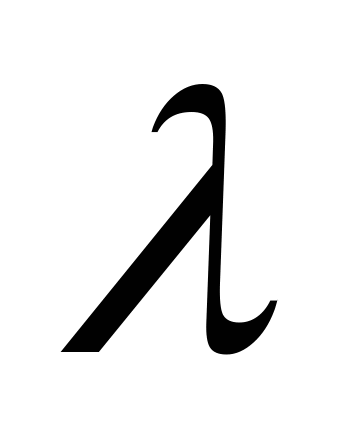 :
: 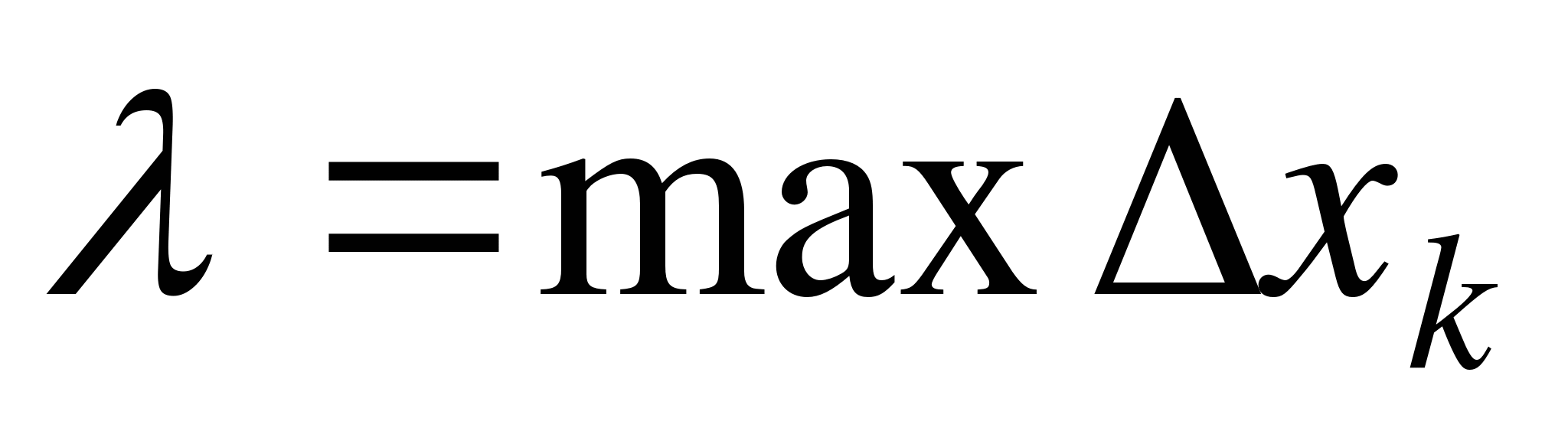 . На каждом частичном отрезке
. На каждом частичном отрезке 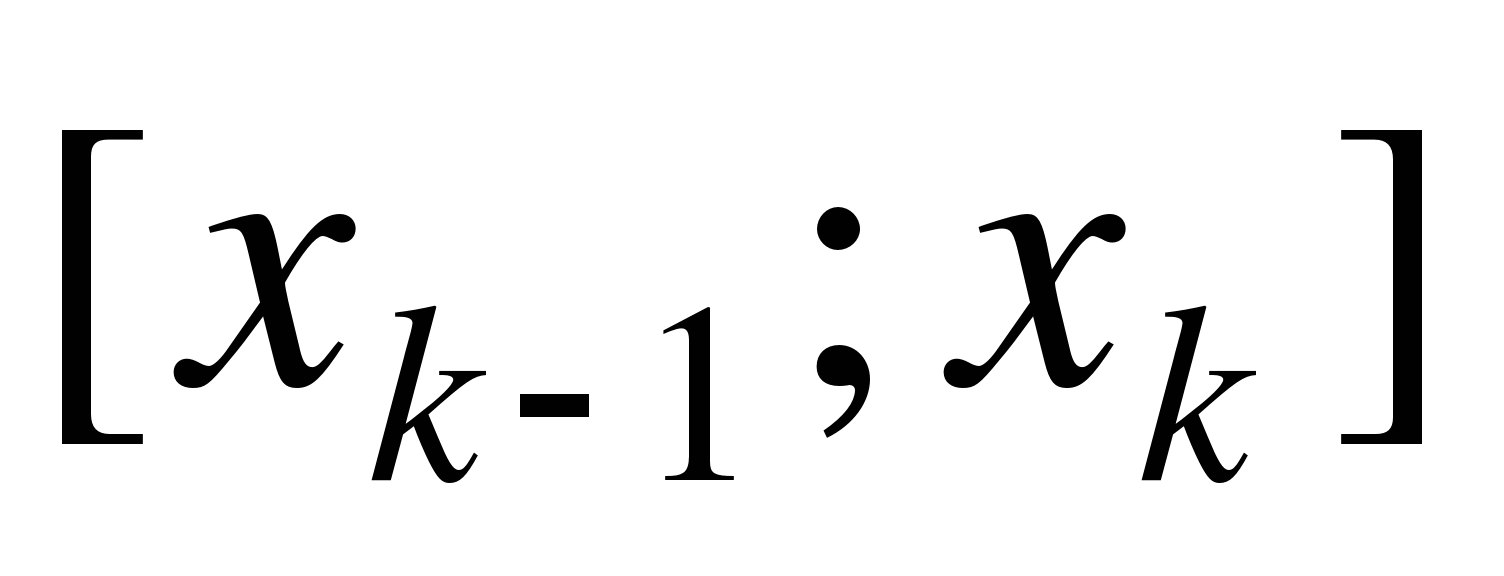 выберем произвольную точку
выберем произвольную точку 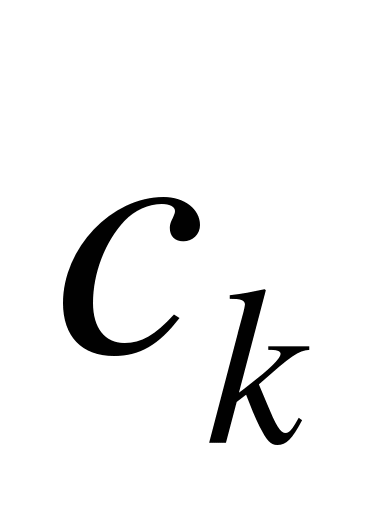 :
: 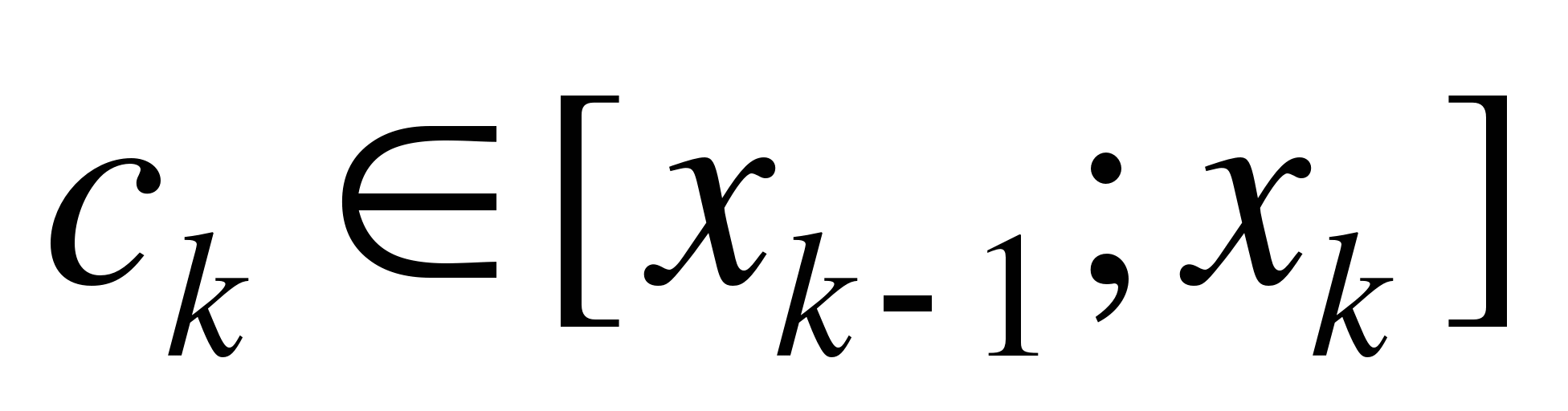 . Произведение
. Произведение 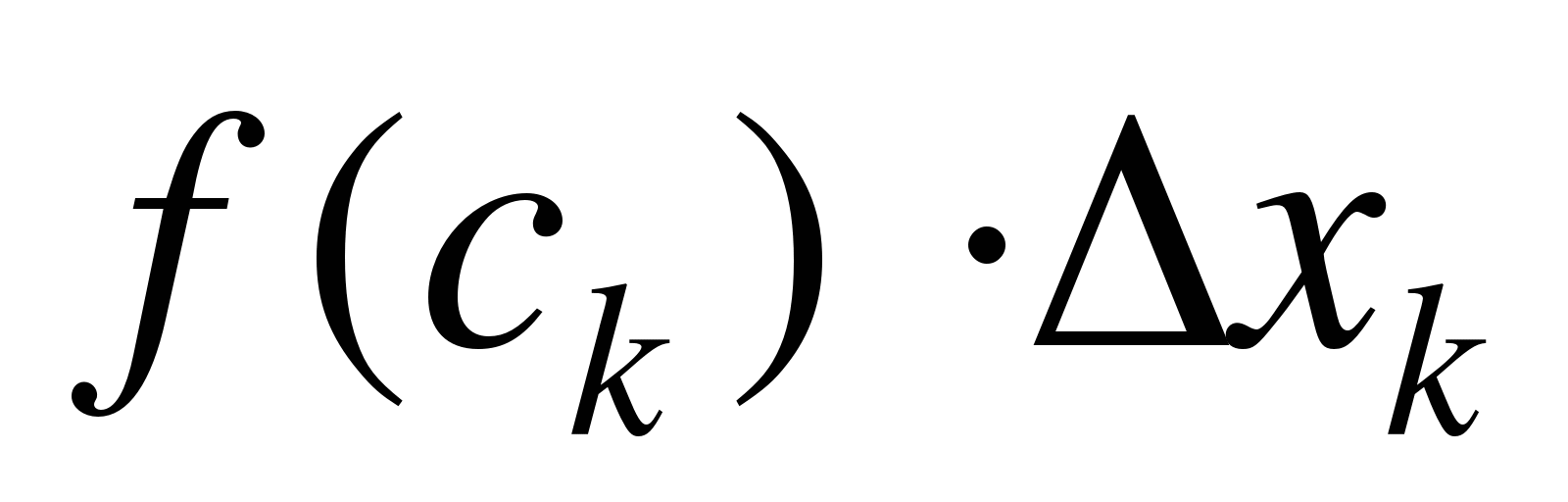 даст площадь прямоугольника с основанием
даст площадь прямоугольника с основанием 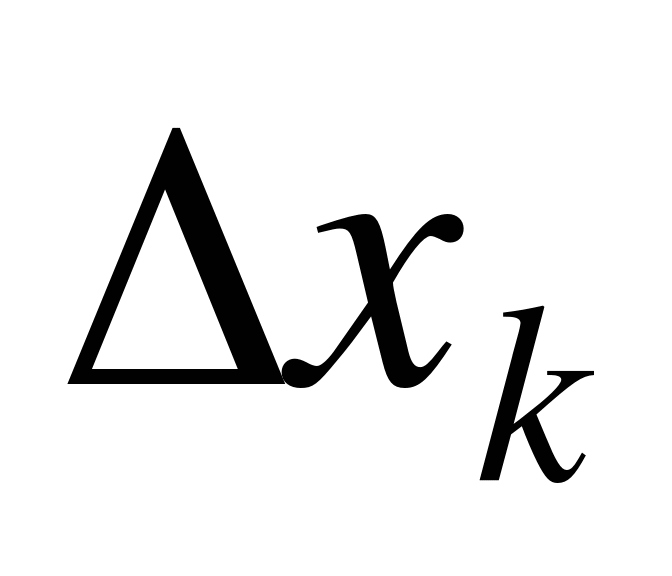 и высотой
и высотой 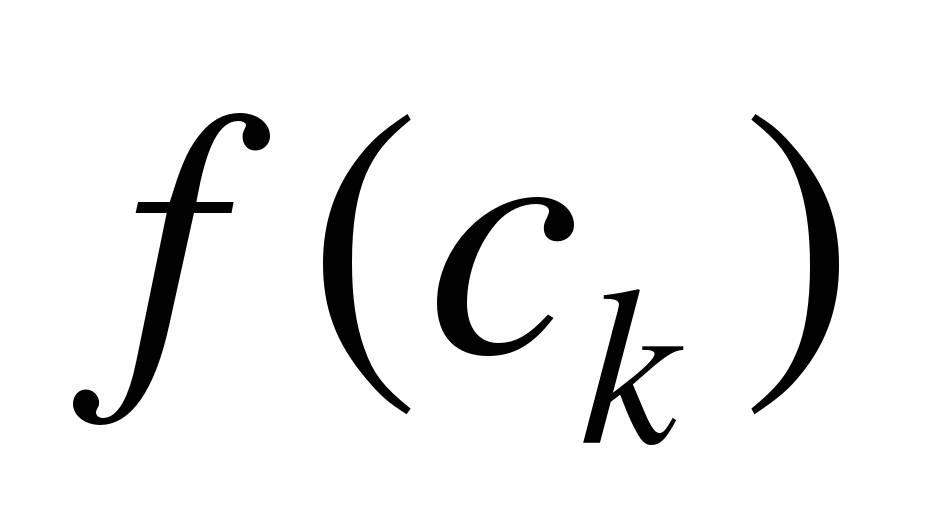 , тогда приближённо площадь
, тогда приближённо площадь  криволинейной трапеции
криволинейной трапеции  равна сумме:
равна сумме:
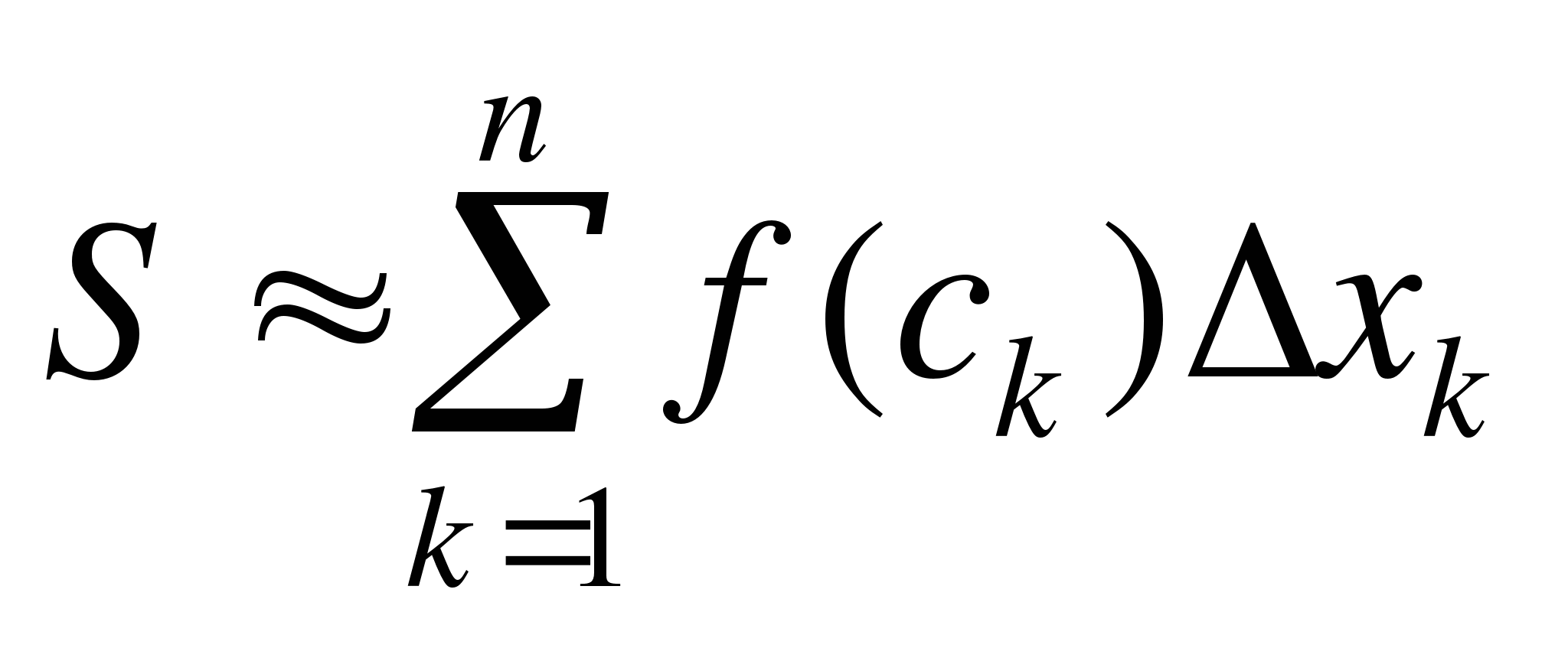 ,
, 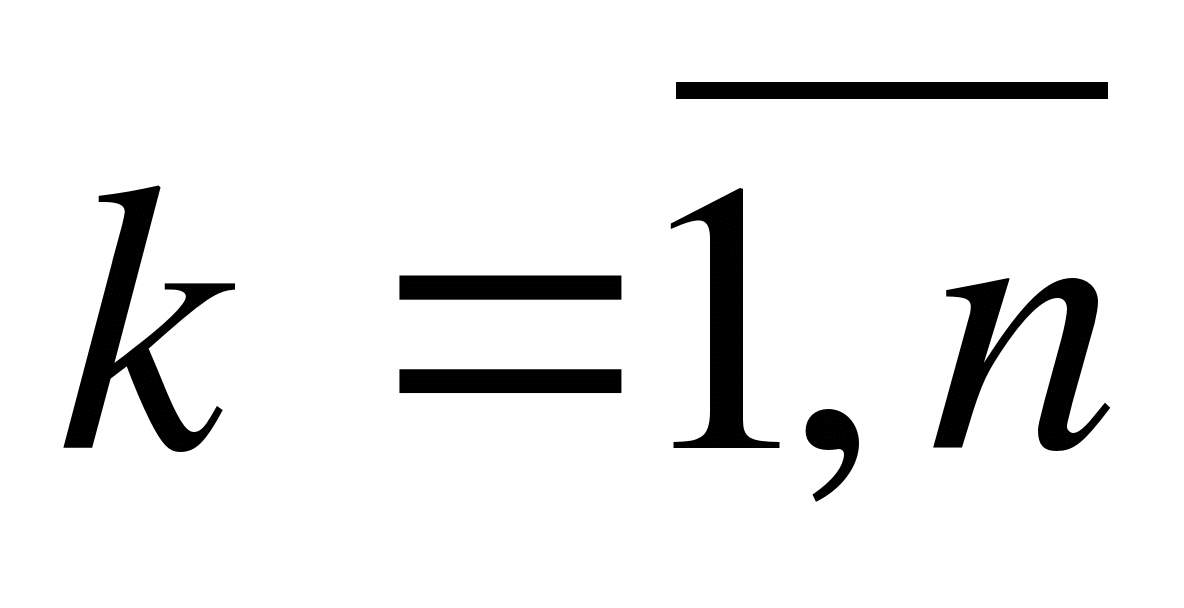 .
.
Эта сумма называется интегральной суммой.
Если увеличить количество частичных отрезков так, что длина любого из них будет стремиться к нулю, то данная интегральная сумма будет стремиться к площади 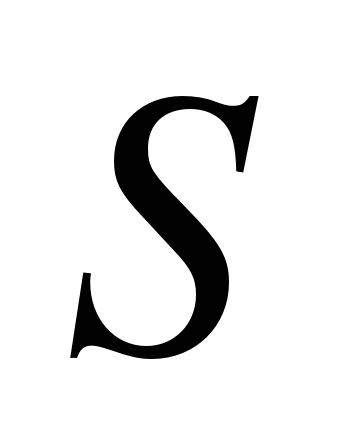 криволинейной трапеции:
криволинейной трапеции:
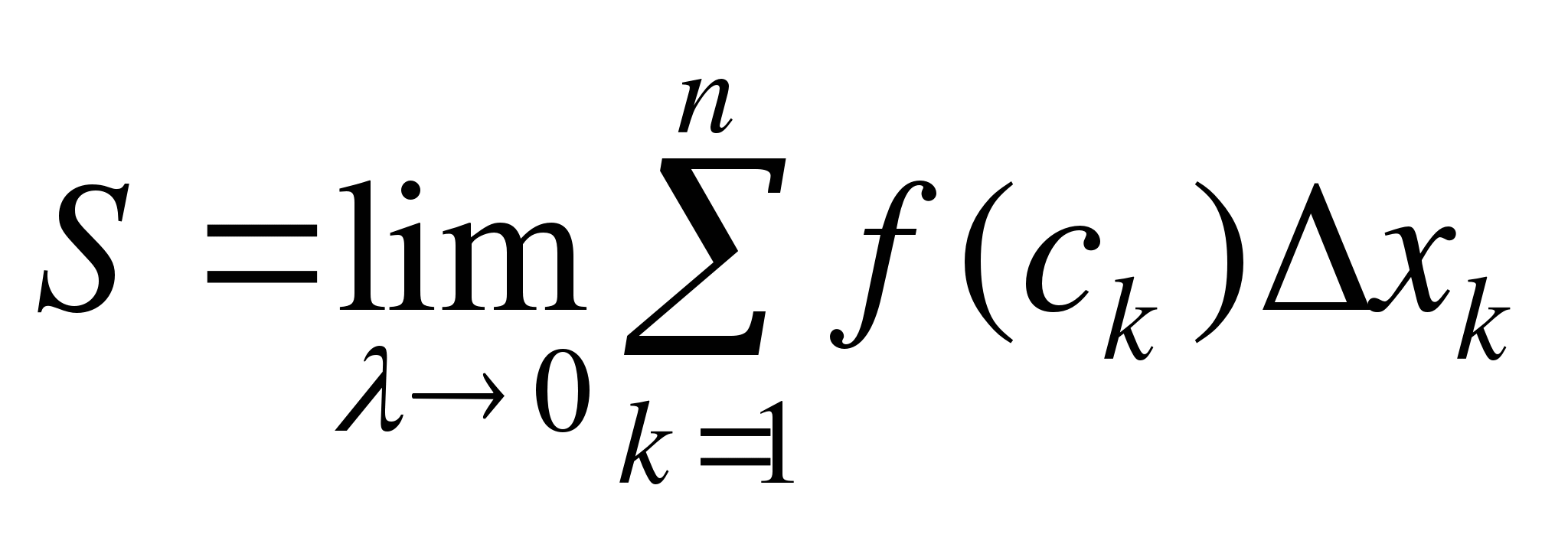 ,
, 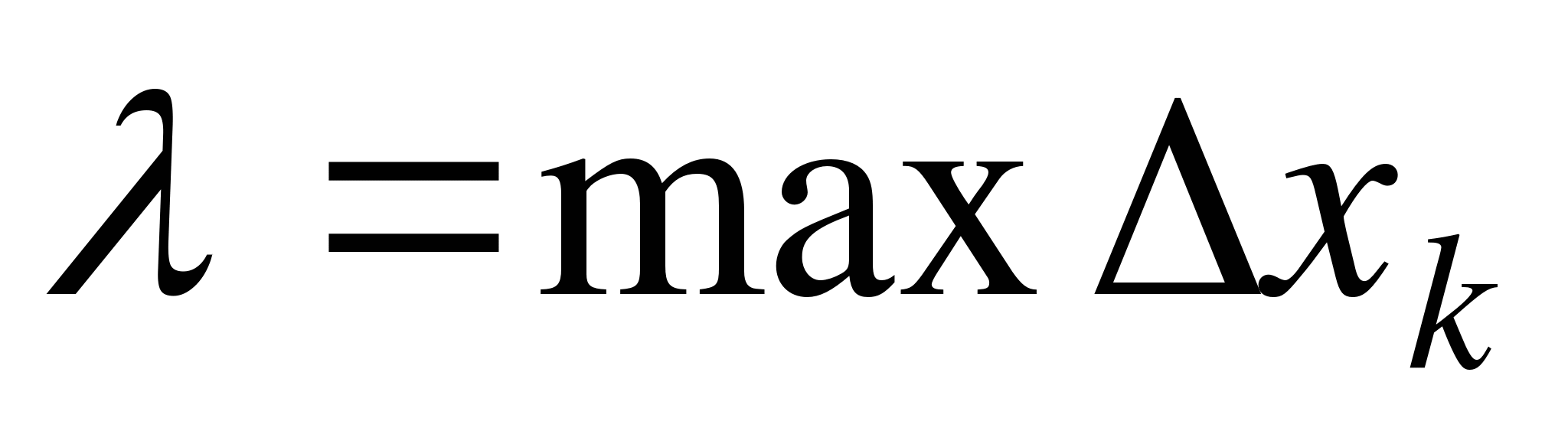 . (1)
. (1)
2. Свойства определённого интеграла
Рассмотрим основные свойства определенного интеграла, считая подынтегральную функцию 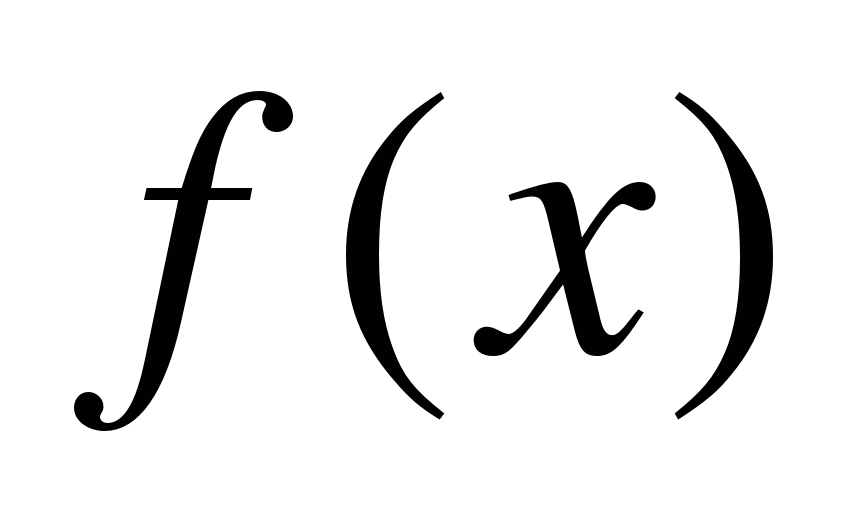 интегрируемой на отрезке
интегрируемой на отрезке 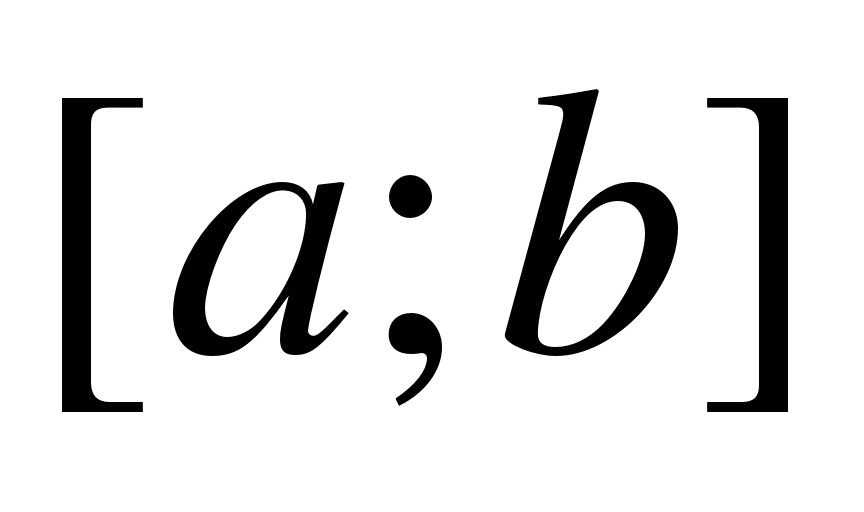 .
.
1. При перестановке пределов интегрирования знак определённого интеграла изменяется:
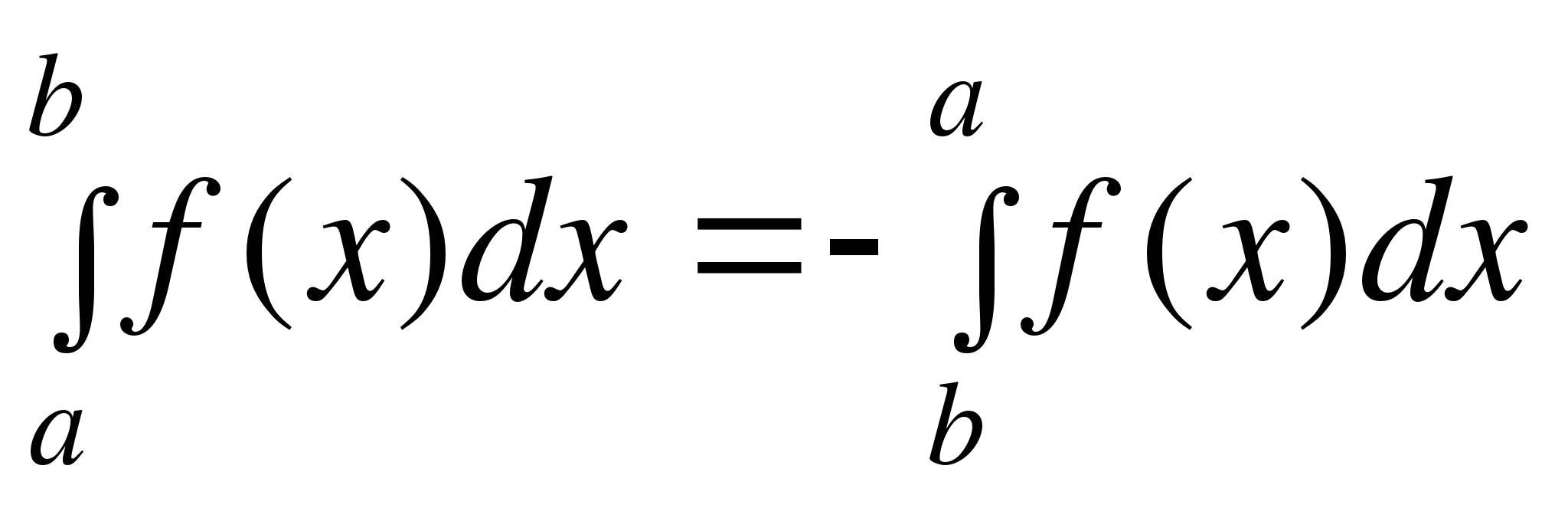 .
.
2. Определённый интеграл от функции с равными пределами интегрирования равен нулю:
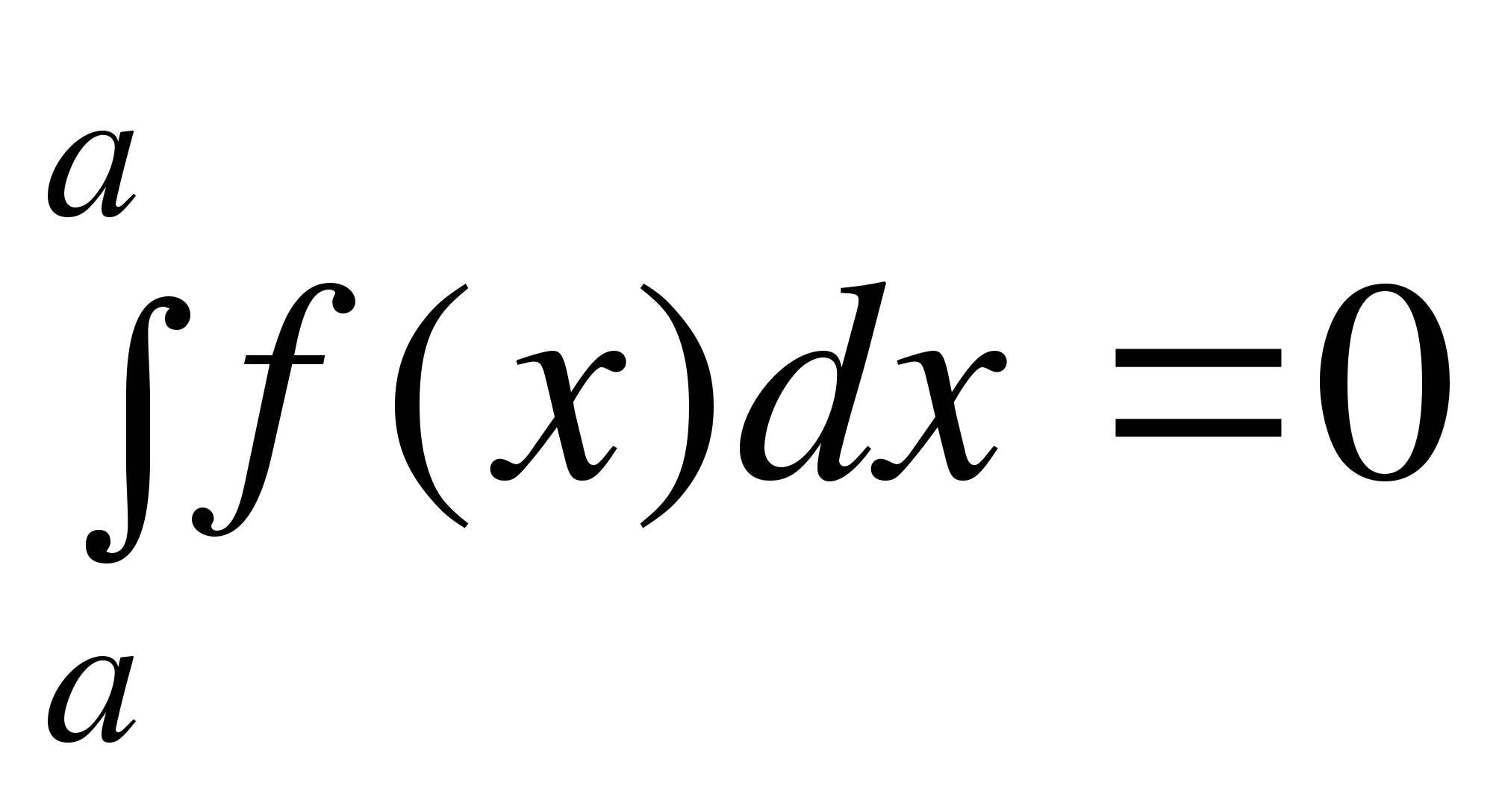 .
.
3. Постоянный множитель можно вынести за знак определённого интеграла:
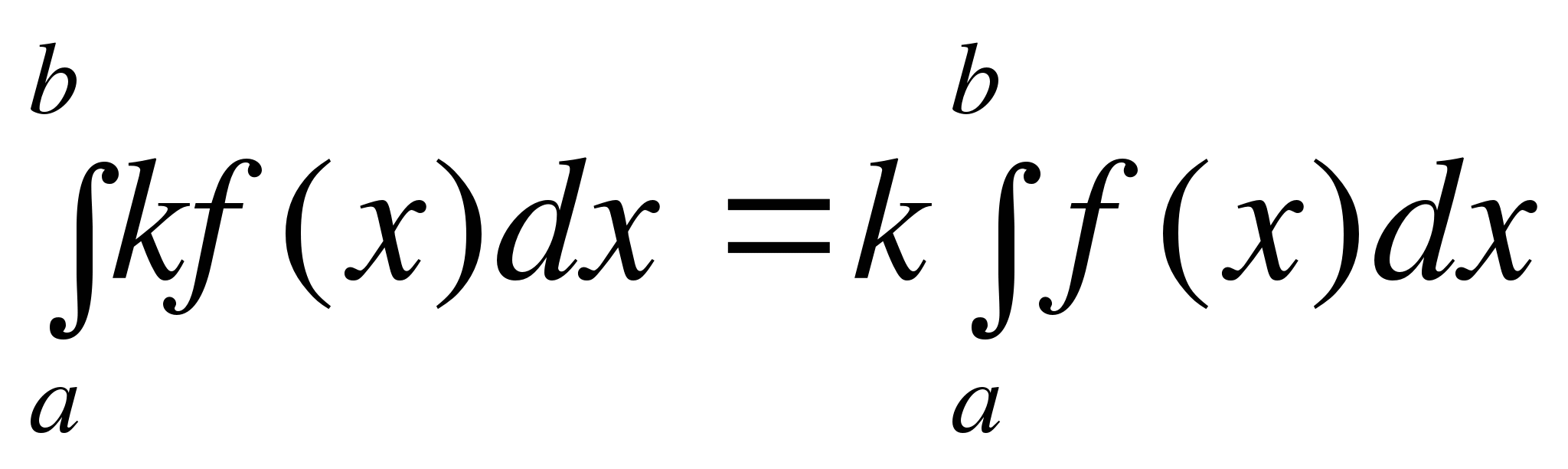 ,
, 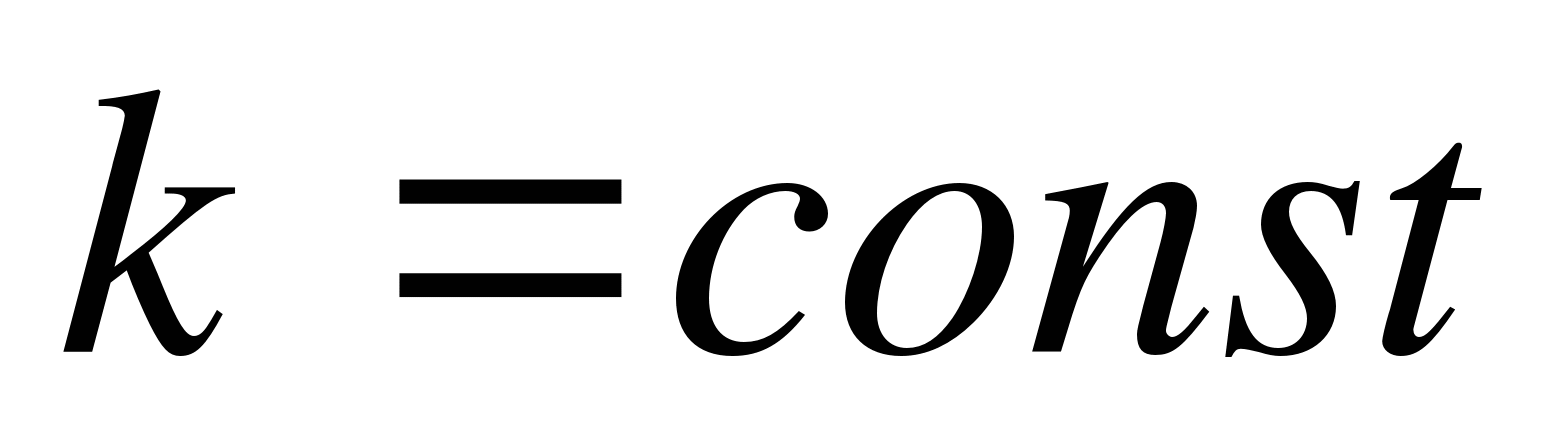 .
.
4. Определённый интеграл от алгебраической суммы двух функций равен алгебраической сумме определённых интегралов от этих функций:
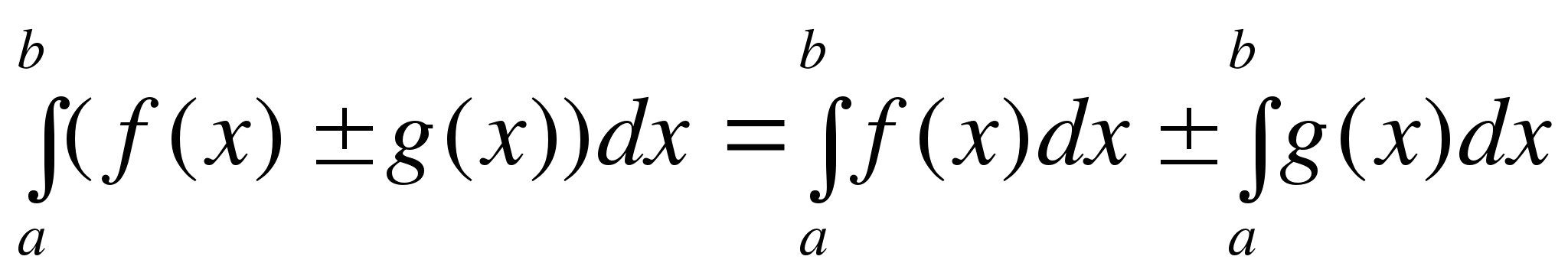 .
.
5. Определённый интеграл по отрезку равен сумме определённых интегралов по его частям:
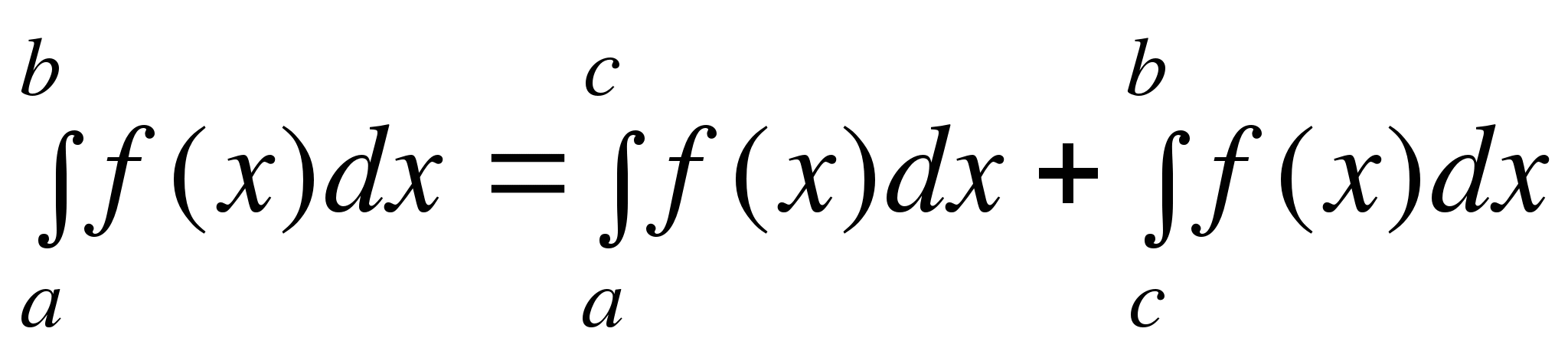 , где
, где 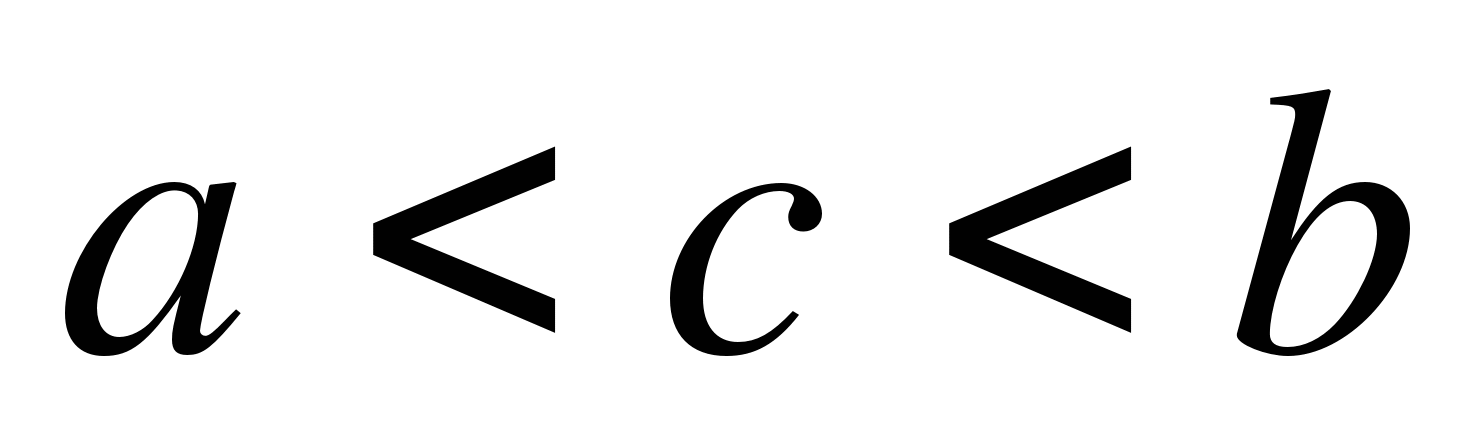 .
.
6. Если функция 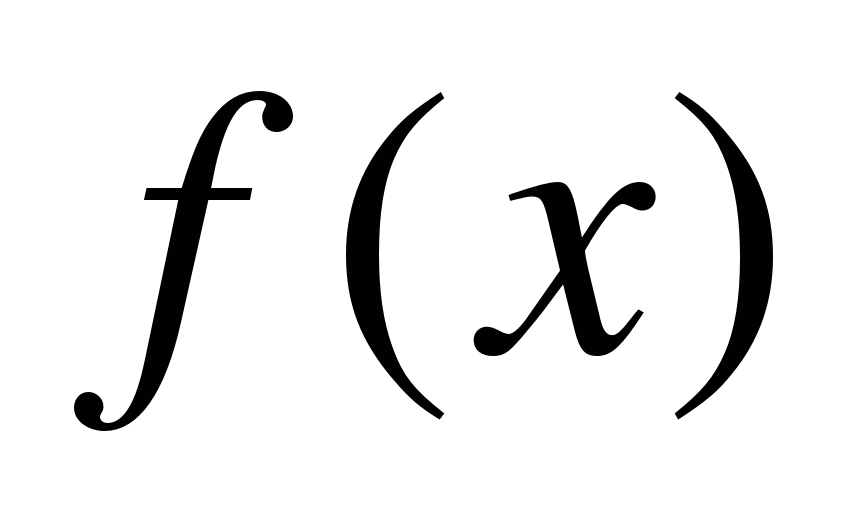 - чётная на отрезке
- чётная на отрезке 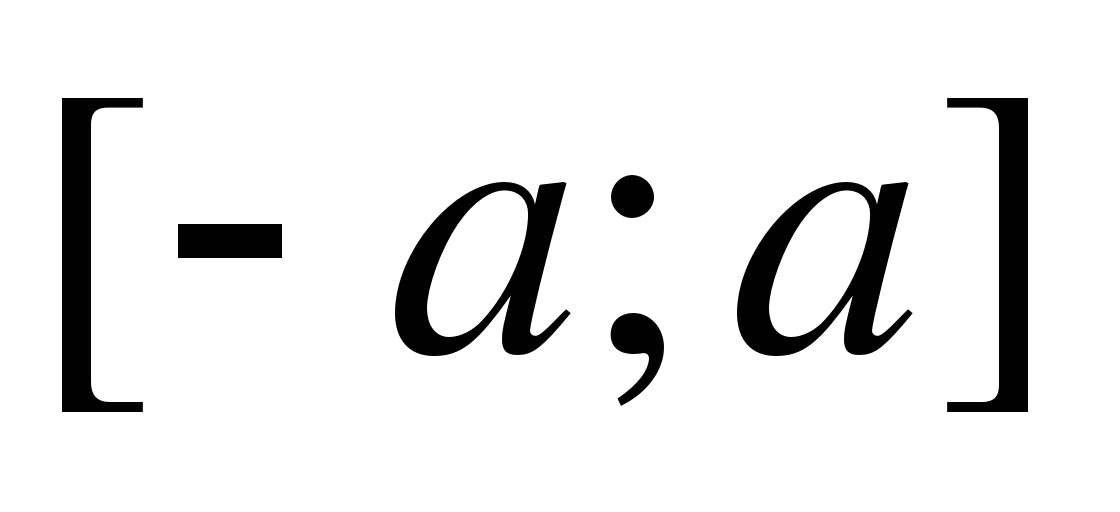 , то выполняется равенство
, то выполняется равенство
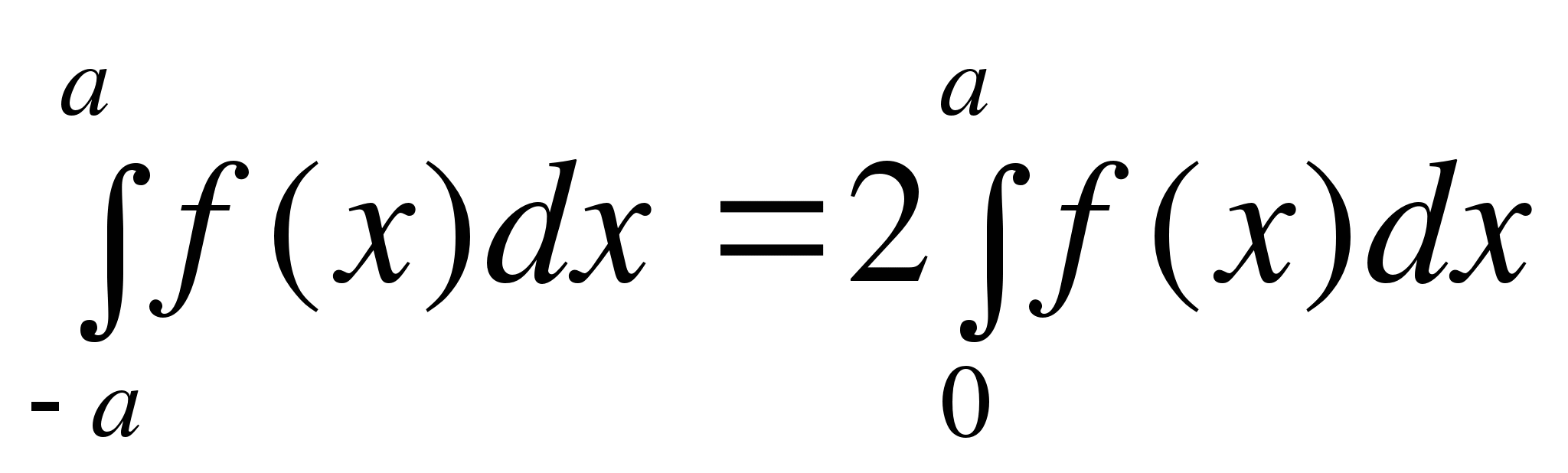 .
.
7. Если функция 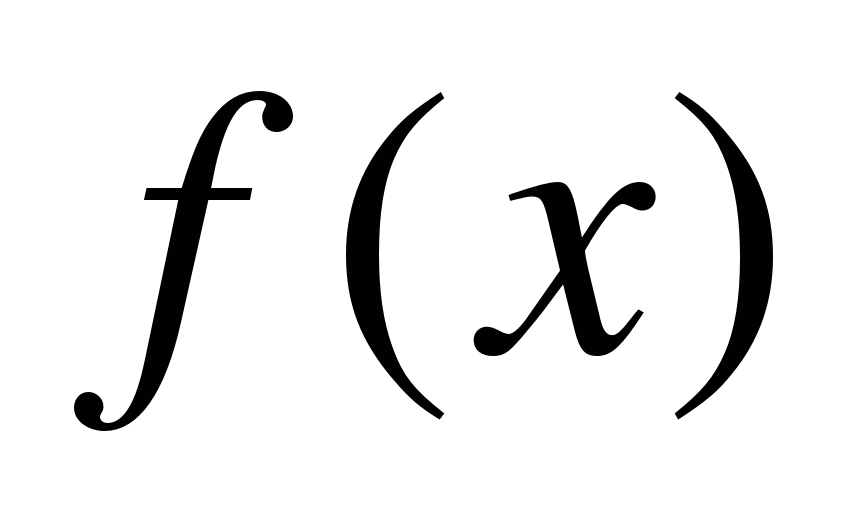 - нечётная на отрезке
- нечётная на отрезке 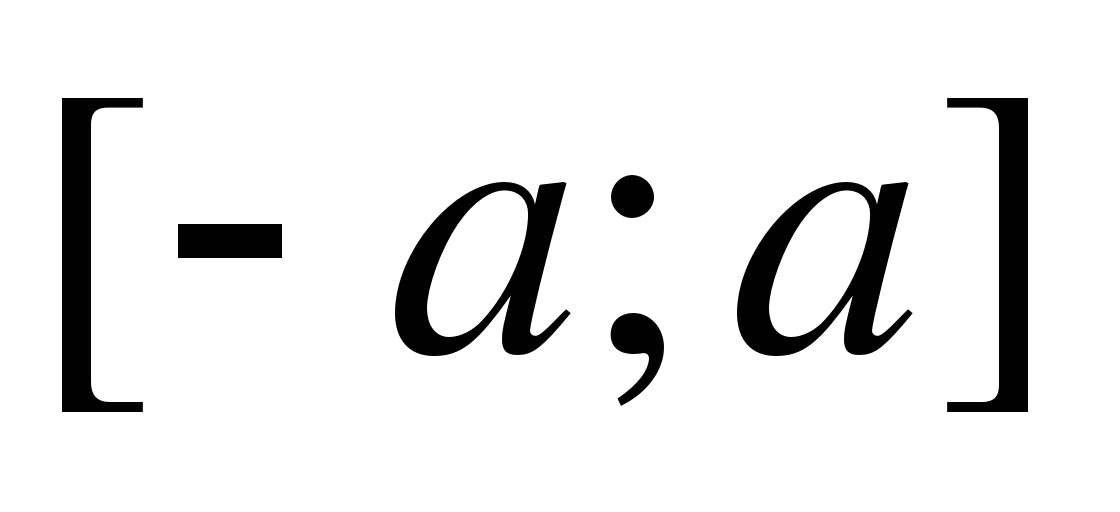 , то выполняется равенство
, то выполняется равенство
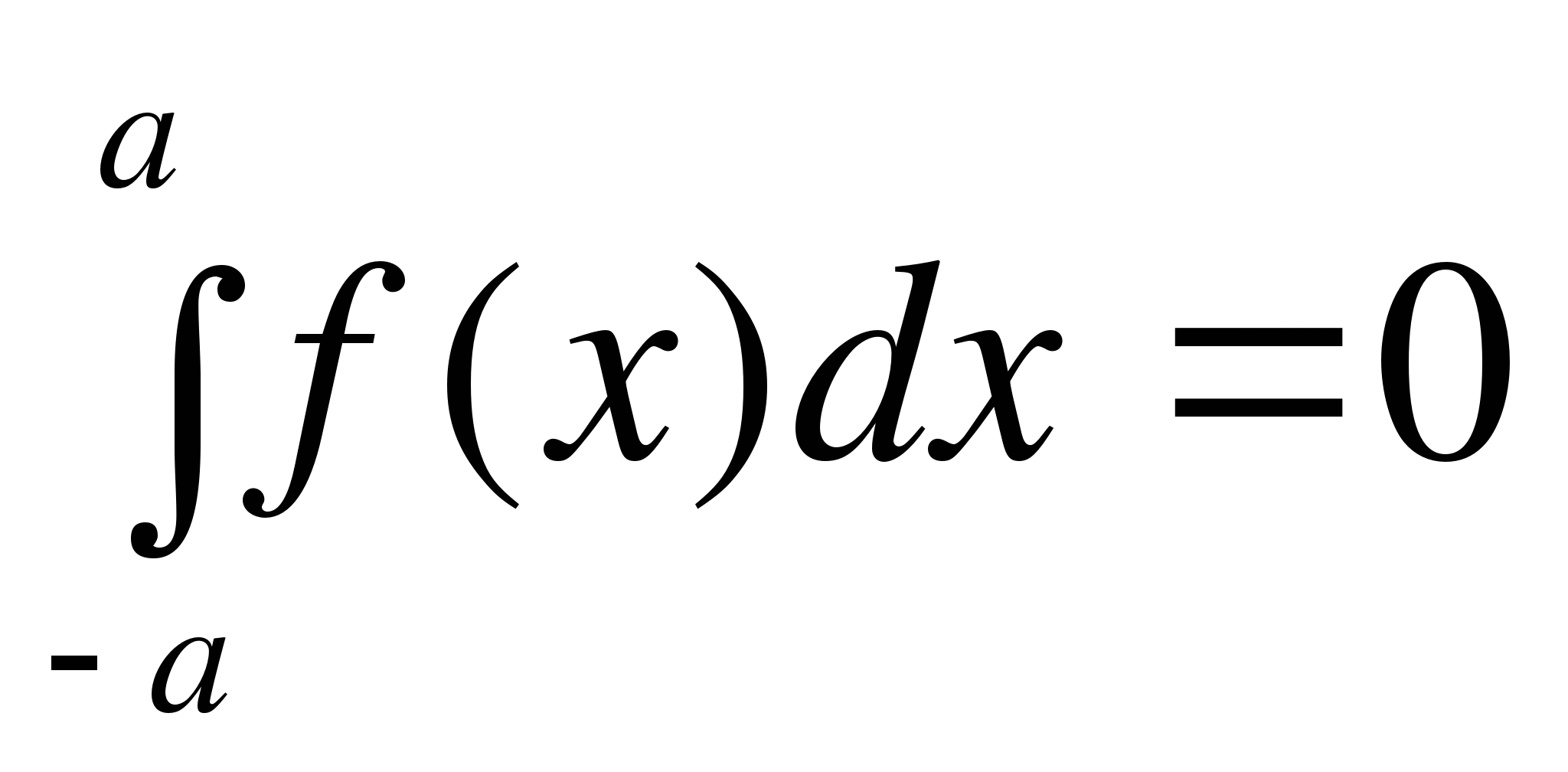 .
.
4. Вычисление определенного интеграла
Теорема. Если функция 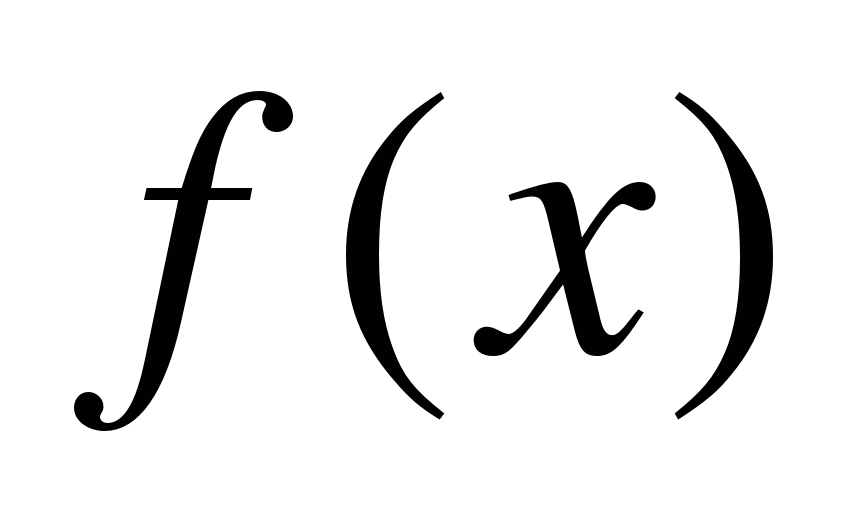 интегрируема на отрезке
интегрируема на отрезке 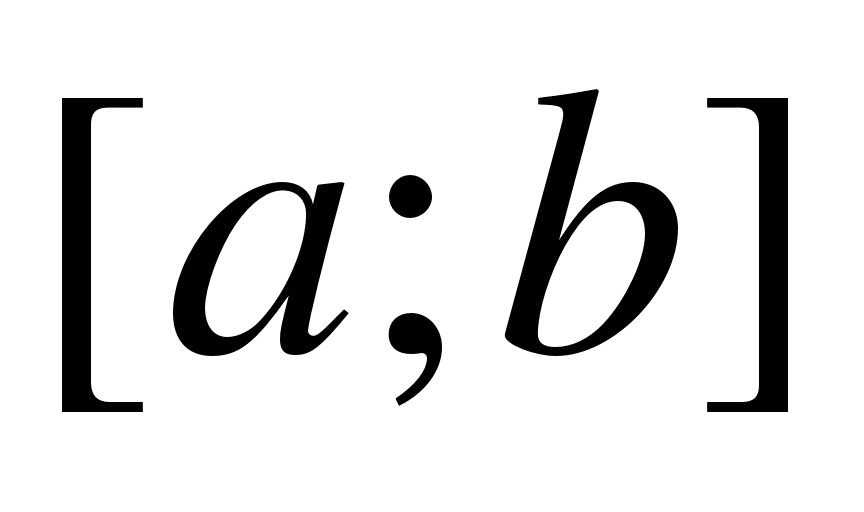 и
и 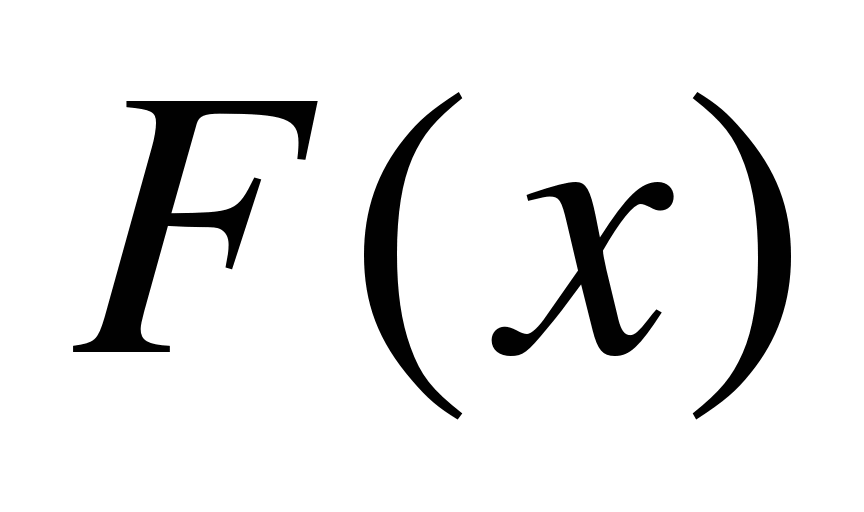 – первообразная функции
– первообразная функции 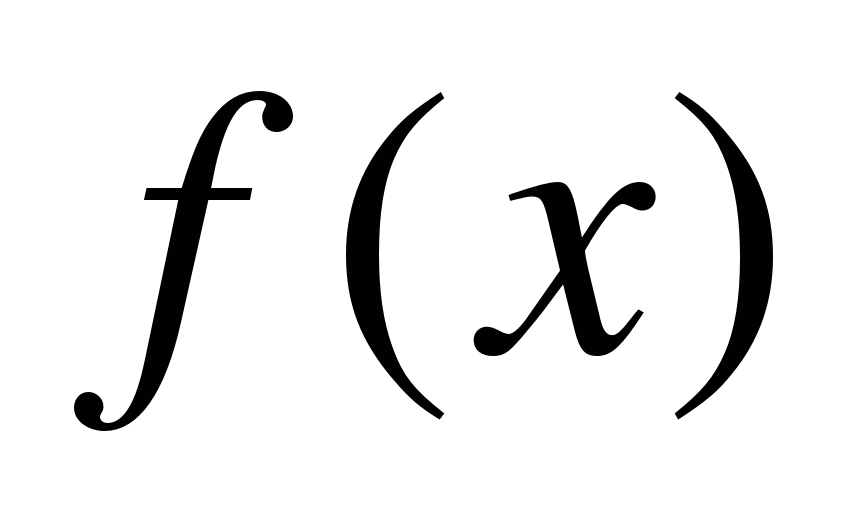 на этом отрезке, то имеет место формула Ньютона–Лейбница:
на этом отрезке, то имеет место формула Ньютона–Лейбница:
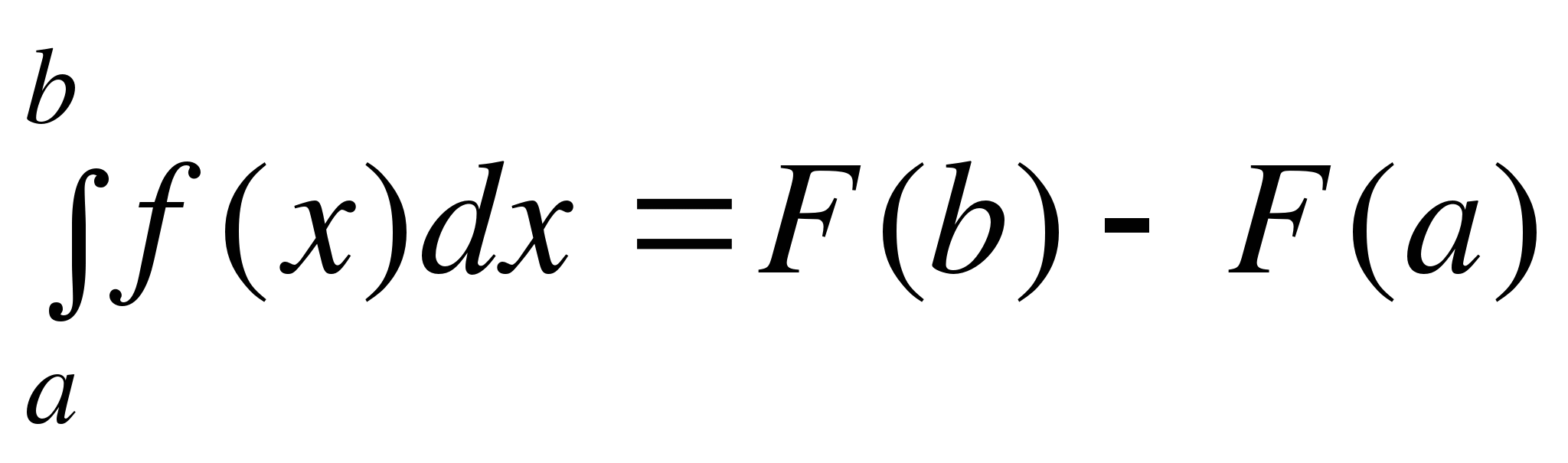 .
.
Эта формула позволяет вычислить определённый интеграл, зная какую-либо первообразную для интегрируемой функции. Первообразную для функции 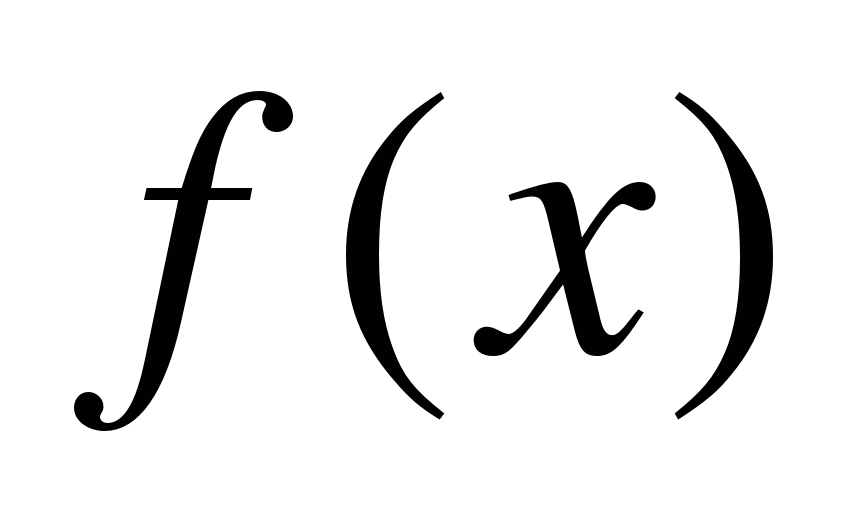 можно найти, вычисляя неопределённый интеграл от этой функции.
можно найти, вычисляя неопределённый интеграл от этой функции.
Замечание.
Для краткости записи употребляется обозначение 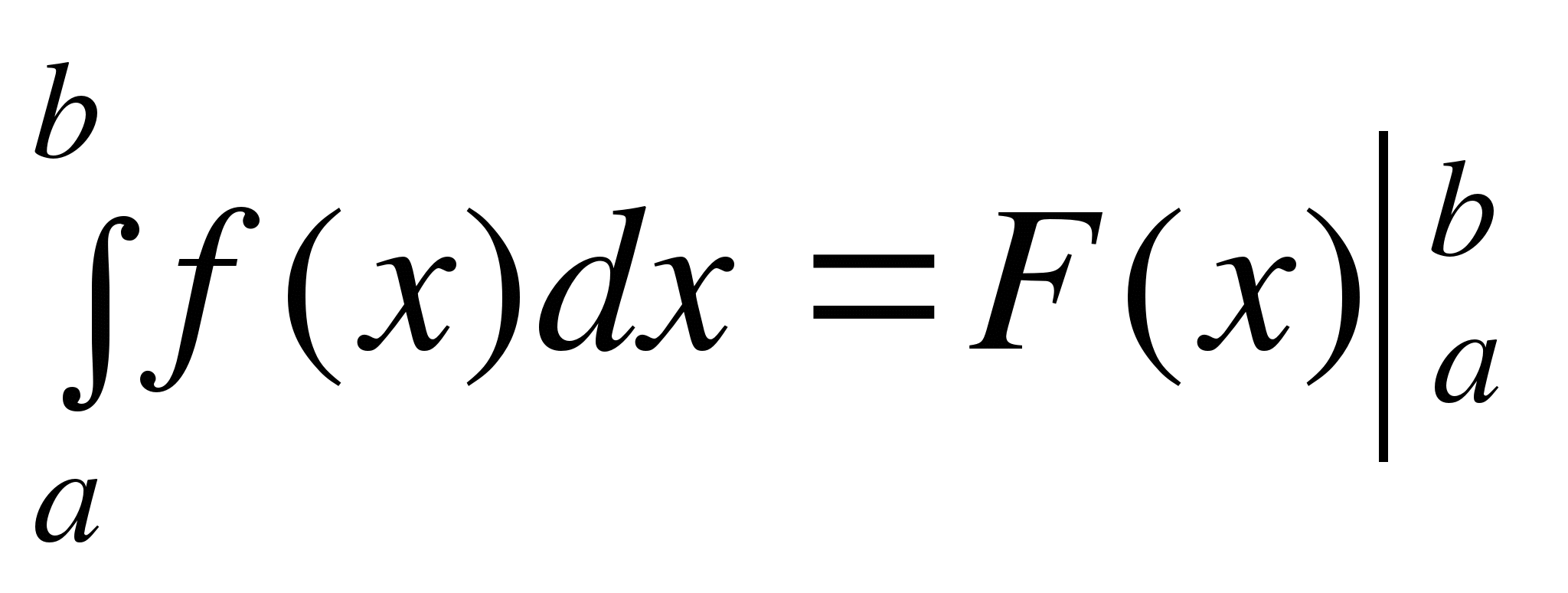 .
.
ПРИМЕРЫ.
1) 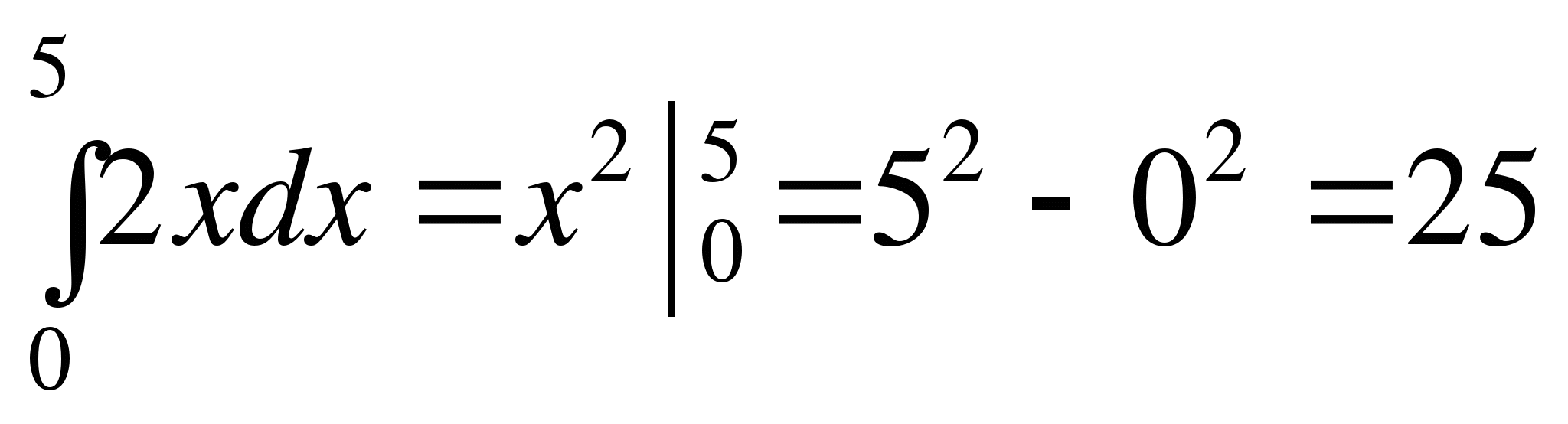 .
.
2) 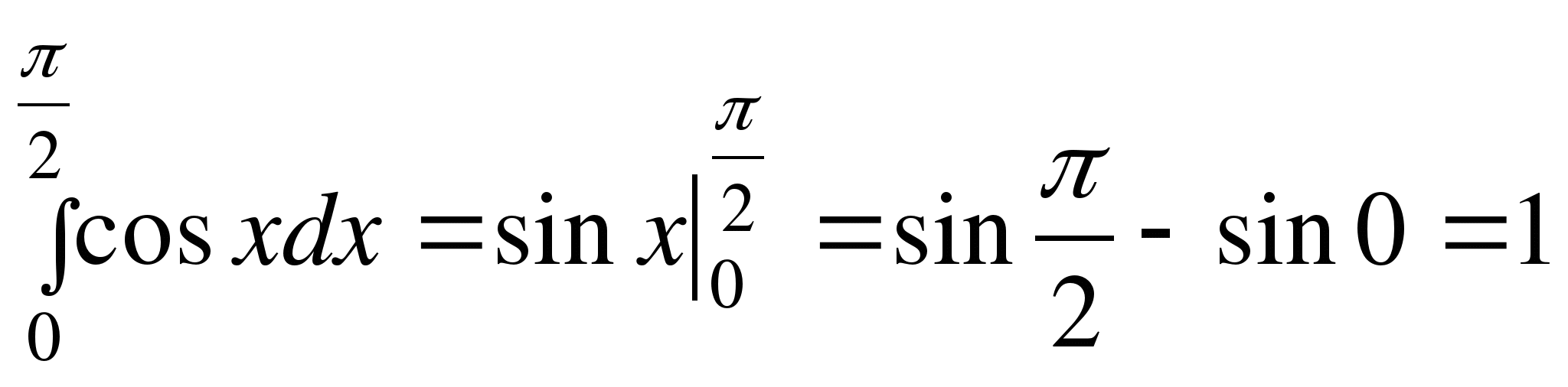 .
.
Вычислить определенный интеграл
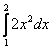
Решение:
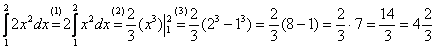
Пример 4: Решение:
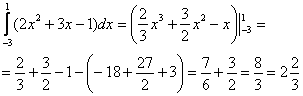 .
.
Домашнее Задание. Пример
Вычислить определенный интеграл
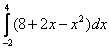






 определена непрерывная и неотрицательная функция
определена непрерывная и неотрицательная функция  .
. ) и отрезками прямых
) и отрезками прямых  ,
,  .
. усть требуется найти площадь криволинейной трапеции.
усть требуется найти площадь криволинейной трапеции. на n частичных отрезков и положим
на n частичных отрезков и положим  ,
,  . Наибольшую из этих разностей обозначим через
. Наибольшую из этих разностей обозначим через  :
:  . На каждом частичном отрезке
. На каждом частичном отрезке  выберем произвольную точку
выберем произвольную точку  :
:  . Произведение
. Произведение  даст площадь прямоугольника с основанием
даст площадь прямоугольника с основанием  и высотой
и высотой  , тогда приближённо площадь
, тогда приближённо площадь  криволинейной трапеции
криволинейной трапеции  равна сумме:
равна сумме: ,
,  .
. ,
,  интегрируемой на отрезке
интегрируемой на отрезке  .
. .
. ,
,  .
. .
. , где
, где  .
. , то выполняется равенство
, то выполняется равенство .
. .
. – первообразная функции
– первообразная функции  .
. .
. .
. .
.

 .
.
 сть требуется найти площадь криволинейной трапеции.
сть требуется найти площадь криволинейной трапеции.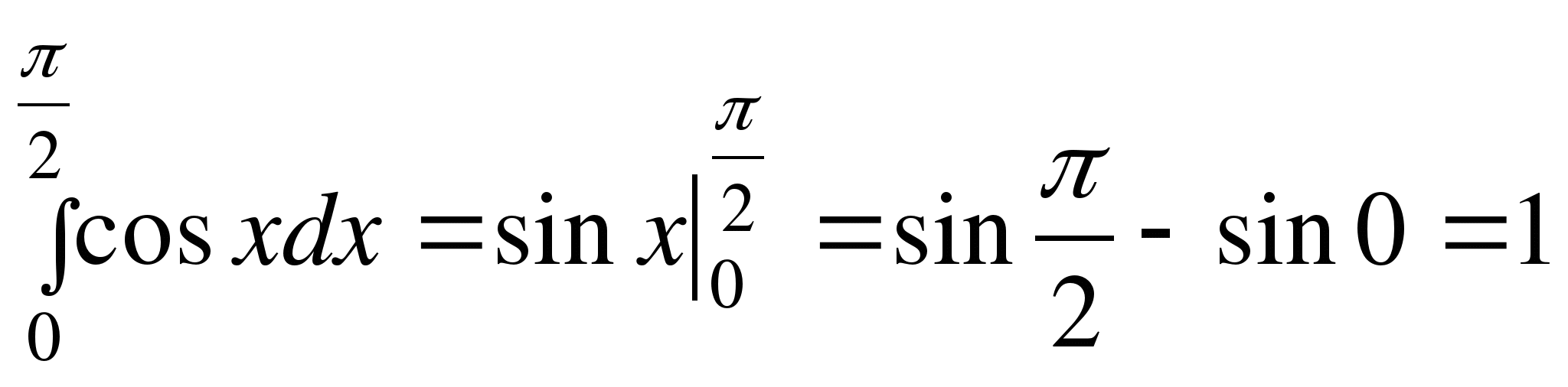 .
.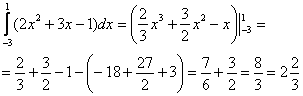 .
.
















