Тайна тайн теоремы Пифагора.

• У Евклида эта теорема гласит (дословный перевод): "В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".
• Латинский перевод арабского текста Аннаирици (около 900 г. н. э. ), сделанный Герхардом Клемонским (начало XII в.), в переводе на русский гласит: "Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол" .
• В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так : "Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу" .
• В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским , теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол" .
• Более строгой надо считать такую формулировку: «Если гипотенуза и катеты прямоугольного треугольника измерены одной и той же единицей длины, то квадрат числового значения длины гипотенузы равен сумме квадратов числовых значений длин катетов».

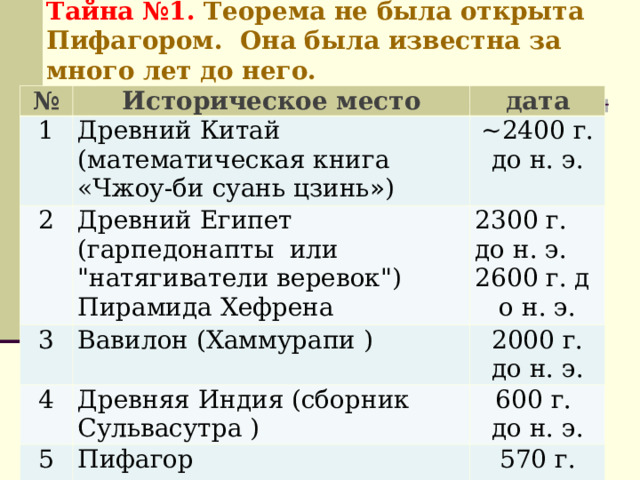
Тайна №1. Теорема не была открыта Пифагором. Она была известна за много лет до него.

№

Историческое место

1

дата

Древний Китай (математическая книга «Чжоу-би суань цзинь » )

2

~2400 г. до н. э.

Древний Египет (гарпедонапты или "натягиватели веревок")

Пирамида Хефрена

3

4

2300 г. до н. э.

2 6 00 г. д

о н. э.

Вавилон (Хаммура п и )

2000 г. до н. э.

Древняя Индия (сборник Сульвасутра )

5

600 г.

до н. э.

Пифагор

570 г.

до н. э.

Клинописные тексты, относящиеся ко времени правления в Вавилоне царя Хаммурапи (около 1950 г. до н. э., то есть более чем за тысячу лет до Пифагора) показывают, что теорема Пифагора была известна вавилонянам не только для частных случаев.

Plimpton 322

Нью-Йорк. Плимптоновский фонд библиотеки Колумбийского университета.

Табличка содержит15 наборов пифагоровых троек, среди которых (четвёртая строка) есть тройка 12709, 13500, 18541:

Самое древнее китайское математико-астрономическое сочинение «Чжоу Би Суан Цзин» ( 周髀算经 ), , написанное около 1100 г. до н.э., в I главе содержит предложения, относящиеся к прямоугольному треугольнику, среди которых — и теорема Пифагора.

Итогом всех математических знаний древних китайцев является трактат «Математика в девяти книгах» (II в. до н.э.), составителем которого является Чжан Цан (ум. 152 г. до н.э.). Трактат содержит 264 задачи без пояснительных текстов. Девятая книга трактата имеет название «Гоу-гу» — так назывались катеты прямоугольного треугольника, причем го у — вертикальный катет (в буквальном переводе — «крюк»), гу — горизонтальный катет («ребро», «связка»).

Все 24 задачи этой главы решаются по «Гоу-гу Теореме" ( 勾股定理 ) , связывающему катеты и гипотенузу прямоугольного треугольника, то есть по теореме Пифагора. В летописях отмечается, что пифагорова тройка 3; 4; 5 была известна в Китае около 2200 г. до н.э.

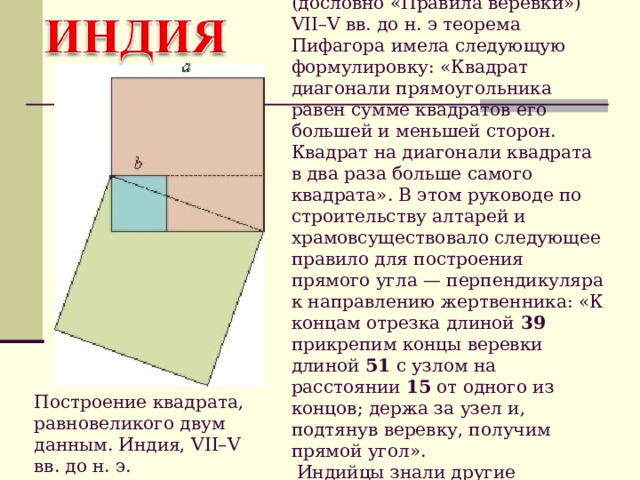
В комментарии к священным книгам – «Ведам», – озаглавленный «Шулва-сутра» (дословно «Правила веревки») VII–V вв. до н. э теорема Пифагора имела следующую формулировку: «Квадрат диагонали прямоугольника равен сумме квадратов его большей и меньшей сторон. Квадрат на диагонали квадрата в два раза больше самого квадрата». В этом руководе по строительству алтарей и храмовсуществовало следующее правило для построения прямого угла — перпендикуляра к направлению жертвенника: «К концам отрезка длиной 39 прикрепим концы веревки длиной 51 с узлом на расстоянии 15 от одного из концов; держа за узел и, подтянув веревку, получим прямой угол». Индийцы знали другие пифагоровы тройки, например , 8; 15; 17 и 12; 35; 37.

Построение квадрата, равновеликого двум данным. Индия, VII–V вв. до н. э.

Крупнейший немецкий историк математики М.Кантор считает, что равенство 3 2 + 4 2 = 5 2 , было известно уже египтянам ещё около 2300 г. до н.э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора, гарпедонапты , или «натягиватели верёвок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Из глубины веков до нас дошло хвастливое утверждение Демокрита (ок. 470 - ок. 380 до н. э.): «В построении линий с доказательствами я никем не был превзойдён, даже так называемыми египетскими гарпедонавтами». В словах Демокрита удивительно упоминание о доказательствах. Но ни в одном египетском или вавилонском тексте ничего похожего на доказательства нет или они просто не дошли до нас?

Пирамида Хефрена ( серединаXXVI века до н. э. ) — вторая по величине древнеегипетская пирамида, расположена рядом с Великим Сфинксом на Плато Гиза. Пирамида изначально имела высоту 143,87 метров. Основание пирамиды представляет собой квадрат со сторонами 215,16 метров

Пр опорции пирамиды Хефрена определяет равнобедренный треугольник. Угол наклона граней— 53,13 °.

Значит высота так относится к половине стороны квадрата, как 4/3, что в свою очередь указывает на 2 прямоугольных треугольника, подобных египетскому (3,4,5)

Строители пирамид были знакомы с теоремой Пифагора и увековечили её.

Тайна №2. Кто дал первым полноценное доказательство теоремы неизвестно.

Пифагорийцы считали автором своего учителя. Но в чём состояло это доказательство и как до него додумался Пифагор ?

Согласно легенде, в знак благодарности он принес богам в жертву 100 быков. Некоторые приписывают Пифагору доказательство, которое Евклид (живший около 300 г. до н.э. в Александрии) приводит в первой книге своих «Начал»; с другой стороны, Прокл, который жил от 410 или 412 г. до 485 в Византии и Афинах, утверждает, что доказательство в «Началах» принадлежит самому Евклиду.

.

Пифагор на фреске Рафаэля (1509 г.)

Тайна №3. Теорема Пифагора – рекордсменка по доказательствам.

Существует в настоящее время более 500 доказательств данной теоремы. Поэтому теорема Пифагора заслужила место в «Книге рекордов Гиннесса» как получившая наибольшее число доказательств. Американский автор Э. Лумис в книге «Пифагорово предложение», вышедшей в 1940 г., собрал 370 разных доказательств! о. Теорема Пифагора привлекательна тем, что сама по себе она вовсе не очевидна.

Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

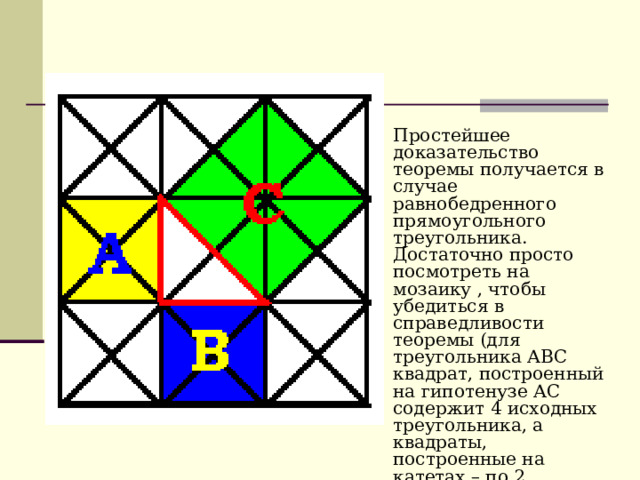
Простейшее доказательство теоремы получается в случае равнобедренного прямоугольного треугольника. Достаточно просто посмотреть на мозаику , чтобы убедиться в справедливости теоремы (для треугольника АВС квадрат, построенный на гипотенузе АС содержит 4 исходных треугольника, а квадраты, построенные на катетах – по 2 треугольника) Теорема доказана.

ДРЕВНЕЕ КИТАЙСКОЕ ДОКАЗАТЕЛЬСТВО

На древнекитайском чертеже 4 равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а+b , а внутренний - квадрат со стороной с , построенный на гипотенузе (рис. б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в 2 прямоугольника (рис. в), то ясно, что образовавшаяся пустота, с одной стороны, равна с 2, а с другой – а 2 + b 2 Теорема доказана. Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые мы видим на

чертеже не используются. По-видимому, древнекитайские математики имели другое доказательство. Именно если в квадрате со стороной с два заштрихованных треугольника (рис. б) отрезать и приложить гипотенузами к двум другим гипотенузам (рис. г),

то легко обнаружить, что полученная фигура,

которую иногда называют «стулом невесты", состоит из двух квадратов со сторонами а и b

Чертеж из трактата "Чжоу-би..." рассматривает египетский треугольник с катетами 3, 4 и гипотенузой 5 единиц измерения.

Квадрат на гипотенузе содержит 25 клеток, а вписанный в него квадрат на большем катете - 16.

Ясно, что оставшаяся часть содержит 9 клеток. Это и будет квадрат на меньшем катете. Теорема доказана.

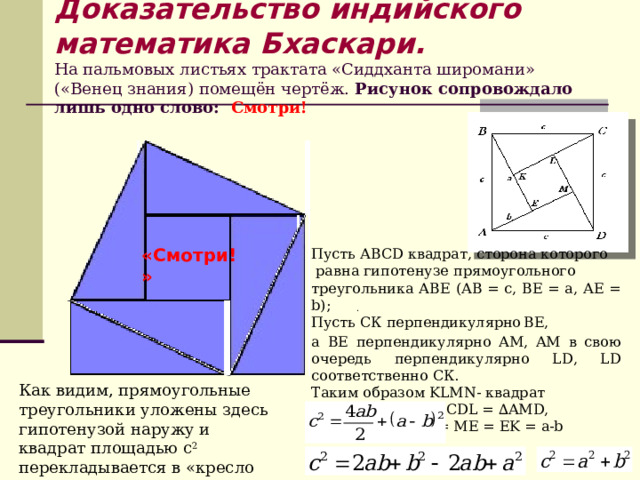
Доказательство индийского математика Бхаскари. На пальмовых листьях трактата «Сиддханта широмани» («Венец знания) помещён чертёж. Рисунок сопровождало лишь одно слово: Смотри!  

«Смотри!»

Пусть АВС D квадрат, сторона которого

равна гипотенузе прямоугольного

треугольника АВЕ (АВ = с, ВЕ = а, АЕ = b );

Пусть СК перпендикулярно ВЕ,

а BE перпендикулярно AM , AM в свою очередь перпендикулярно LD , LD соответственно СК.

Таким образом KLMN - квадрат

ΔABE = ∆BCK = ∆CDL = ∆AMD,

значит KL = LM = ME = EK = a-b

.

Как видим, прямоугольные треугольники уложены здесь гипотенузой наружу и квадрат площадью с 2 перекладывается в «кресло невесты» с площадью а 2 +в 2

Абу-л-Хасан Са́бит ибн

Курра ал-Харрани ас-Саби

(араб. ثابتبنقرةبنمروان ‎‎ , англ.  Thābit ibn Qurra al-Harrānī Al-Sābi

, Харран, 836 — Багдад, 18 февраля 901) — астроном,

математик и врач IX века,сириец по происхождению

В русской литературе также упоминается

как Сабит ибн Корра или Табит ибн Курра .

Был учеником знаменитых математиков братьев Бану Муса,

работал в «Доме мудрости» в Багдаде.

Его доказательство теоремы Пифагора

протекает в виде трансформации « стула невесты » ,

состоящего из 2 квадратов.

Доказательство президента США

Джеймса Гарфилда (1882 г.)

Доказательство президента США

Джеймса Гарфилда (1882 г.)

Расположим два равных прямоугольных треугольника так, чтобы катет одного из них был продолжением другого.

Площадь рассматриваемой трапеции находится как произведение полусуммы оснований на высоту S = 0,5 (а+в)(а+в)

C другой стороны, площадь трапеции равна сумме площадей полученных треугольников:

S = 0,5 ав+ 0,5 ав+ 0,5 с 2

Приравнивая данные выражения, получаем:

0,5(а+в)(а+в)= 0,5 ав+ 0,5 ав+ 0,5 с 2

(а+в)2=2ав+с2

а 2 +2ав+в 2_ 2ав=с 2

или с 2 = a 2 + b 2

Доказательство Евклида

Квадрат на левом катете – A DEC – равновелик удвоенному треугольнику DAB , потому что у них общее основание DA и общая высота A C =  DE . Треугольник DAB равен треугольнику CAK по двум сторонам и углу между ними: DA  =  CA , AB равно AK , DAB  =  DAC +  CAB  =   90°   +  CAB =   BAK  +  CAB  =  CAR Треугольник CAK равновелик половине прямоугольника AHJK , потому что у них общее основание AK и общая высота AH = JK . Таким образом, квадрат A DEC равновелик прямоугольнику AHJK . Точно так же доказывается, что квадрат на правом катете – BCFG – равновелик прямоугольнику JHBI . Следовательно, оба квадрата на катетах, вместе взятые, равновелики квадрату ABIK на гипотенузе.

« Начала» Евклида вплоть до XX  были вторым бестселлером после Библии. Поэтому учащиеся средних веков сталкивались с доказательством теоремы Пифагора именно по Евклиду и считали его очень трудным. Они называли его elefuga- бегство "убогих", так как некоторые ученики, не имевшие серьезной математической подготовки, бежали от геометрии.

Или Dons asinorum- ослиный мост ,так как слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому "ослами " , были не в состоянии осилить теорему Пифагора, служившую для них вроде непреодолимого моста.

Из-за чертежей, сопровождающих теорему Пифагора, учащиеся прозвали

ее также "ветряной мельницей", рисовали карикатуры, а русские гимназисты составили шуточные стихи : «Пифагоровы штаны на все стороны равны ». Кстати, в русской литературе, возможно, "пифагоровы штаны" впервые использовал Достоевский в "Селе Степанчикове" (1859). Значит, появилось это высказывание в 1830-е годы, когда Федор Михайлович обучался в частном пансионе Чермака (Москва), а затем в военно-инженерном училище (Петербург )

"Пифагоровы штаны во все стороны равны " .

Доказательство Анариция (багдадский математик и астроном X в. ан-Найризий (латинизированное имя – Анариций).

Доказательство основывается на том, что равносоставленные фигуры равновелики: квадраты, построенные на катетах и гипотенузе, разбиваются на многоугольники так, что каждому многоугольнику из состава квадрата на гипотенузе соответствует равный многоугольник одного из квадратов на катетах.

Любопытно, что доказательство Аннариция является простейшим

среди огромного числа доказательств теоремы Пифагора методом разбиения:

в нем фигурирует всего 5 частей (или 7 треугольников).

Это наименьшее число возможных разбиений».

Доказательство Адриен Мари Лежандра, основанное на теории подобия

Из подобия треугольников следует:

Адриен Мари Лежа́ндр ( фр.  Adrien-Marie Legendre , 18 сентября1752, Париж — 10 января1833, там же) — французский математик

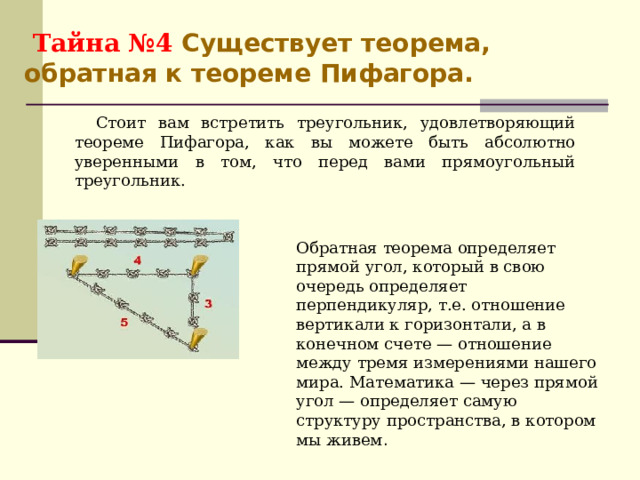
Тайна №4 Существует теорема, обратная к теореме Пифагора.

Стоит вам встретить треугольник, удовлетворяющий теореме Пифагора, как вы можете быть абсолютно уверенными в том, что перед вами прямоугольный треугольник.

Обратная теорема определяет прямой угол, который в свою очередь определяет перпендикуляр, т.е. отношение вертикали к горизонтали, а в конечном счете — отношение между тремя измерениями нашего мира. Математика — через прямой угол — определяет самую структуру пространства, в котором мы живем .

Тайна № 5. ИРРАЦИОНАЛЬНЫЕ ЧИСЛА

Вычисляя диагональ квадрата, пифагорейцы открыли, но отказывались признать существование иррациональных чисел. Легенда рассказывает о том, что один из учеников по имени Гиппас так и не сумел найти эквивалентную обыкновенную дробь числу √2.Открытие Гиппаса разрушило мир рациональных чисел и могло бы повлечь за собой период споров и сомнений. Гиппаса приговорили к смерти через утопление.

Иррациональное число (лат.irrationalis — неразумный, от лат.in(ir) — отрицательная приставка и лат.ratio — счёт, отношение) — вещественное число, не являющееся рациональным (т. е. целым или дробным). Действительные иррациональные числа могут быть представлены бесконечными непериодическими десятичными дробями.

Times New Roman ( Заголовки)

√ 2 = 1,414 213 562 373 095 048 801 688 724

Йельская Вавилонская коллекция

Тайна № 6. ПИФАГОРОВЫ ЧИСЛА

Пифагор дополнил данную теорему собственными исследованиями, тем самым повысив её значимость в мире математических открытий. В частности пифагорийцы активно искали тройки натуральных чисел, удовлетворяющих уравнению (а 2 + b 2 = c 2 ) . Эти числа так и называют пифагоровыми тройками

Евклид сумел доказать, что существует бесконечно много таких пифагоровых троек.

Предложенное Евклидом доказательство начинается с наблюдения:

разность квадратов последовательных целых чисел всегда равна какому-нибудь

нечетному числу:

Прибавив каждое из бесконечного множества нечетных чисел к соответствующему

квадрату, мы получим другой квадрат. Некоторые нечетные числа, составляющие

часть всех нечетных чисел, сами являются квадратами (например, 9=3 2 , 25=5 2 , 49=7 2

и т. д.). Следовательно, существует бесконечно много нечетных квадратов, которые

Можно прибавить к квадрату и получить другой квадрат. Иначе говоря, существует

бесконечно много пифагоровых троек.

Тайна №7. Теорема Пифагора - источник для множества

обобщений и плодородных идей.

Один из наиболее блестящих и загадочных математиков в истории Пьер де Ферма «испортил» уравнение Пифагора x 2 + y 2 = z 2 . Он всего лишь изменил степень на единицу, но его новое уравнение x 3 + y 3 = z 3 не допускало никаких решений в целых числах. Незначительное изменение превратило уравнение, допускающее бесконечно много решений в целых числах, в уравнение, не имеющее ни одного решения в целых числах.

Попробовав заменить степень 2 на целые числа бóльше 3, он обнаружил, что найти решение в целых числах каждого из этих уравнений очень трудно. На полях «Арифметики» Диофанта, рядом с задачей про пифагоровы тройки, Ферма оставил такое замечание: «Невозможно для куба быть записанным в виде суммы двух кубов, или для четвертой степени быть записанной в виде суммы двух четвертых степеней, или, в общем, для любого числа, которое есть степень больше двух, быть записанной в виде суммы двух таких же степеней. Я нашел поистине удивительное доказательство этого предложения, но поля здесь слишком узки для того, чтобы вместить его» . Это замечание Ферма сделал в1637 году. Ферма никогда не раскрывал своих доказательств и это был вызов математическому сообществу.

ТЕОРЕМА ФЕРМА : уравнение x n + y n = z n не имеет

решения в целых числах при n больше 2

358 лет многие великие математики пытались доказать эту теорему, но …

Эндрю Уайлс в возрасте десяти лет, когда он впервые узнал о Великой теореме Ферма

23 июня 1993 года американский математик Эндрю Уайлс выступил с лекцией в Институте сэра Исаака Ньютона в Кембридже.

На снимке вы видите Уайлса через мгновенье после того, как он объявил о найденном им доказательстве Великой теоремы Ферма

Дерево Пифагора — разновидность основанная на фигуре, известной как «Пифагоровы штаны».

Впервые дерево Пифагора построил А. Е. Босман (1891—1961) во время второй мировой войны, используя обычную чертёжную линейку.

Обдуваемое ветром

дерево Пифагора

КАТЕТ

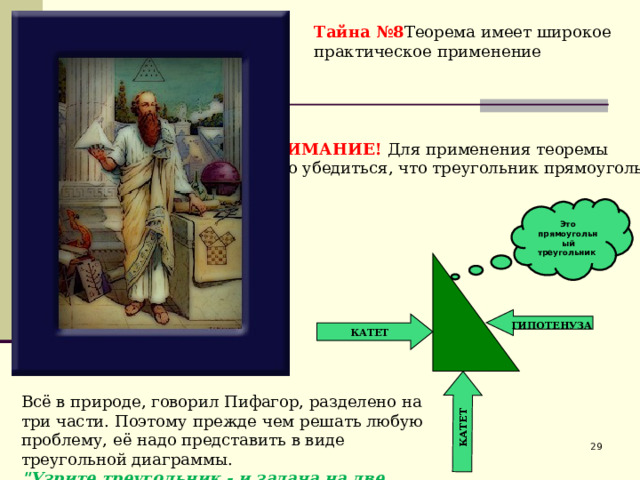
Тайна №8 Теорема имеет широкое практическое применение

ВНИМАНИЕ! Для применения теоремы

надо убедиться, что треугольник прямоугольный

Это прямоугольный треугольник

ГИПОТЕНУЗА

КАТЕТ

Всё в природе, говорил Пифагор, разделено на три части. Поэтому прежде чем решать любую проблему, её надо представить в виде треугольной диаграммы.

"Узрите треугольник - и задача на две трети решена".

В Абдерах в 430—420-х гг. до н. э. (т. е. менее чем через 100 лет после смерти Пифагора) были впервые выпущены монеты с чеканным изображением человека. Это был Пифагор

Самосская монета с изображением Пифагора. II - III вв. Прорисовка.

О чем мне рассказал музейный экспонат

МОИ ИССЛЕДОВАНИЯ

При увеличении диаметра монеты до 13 см, проведённые замеры показали любопытные результаты:

Высота буквы равна 1см. Количество складок на одежде Пифагора 13. (1х 13=13 (см)).Возможно высота буквы выбрана за меру измерения монеты.

Рука ограничивает шест на расстоянии 8 см. Отрезок от точки руки на шесте до буквы М в слове Самос равен 6см. Опустив перпендикуляры к основанию и к шесту, получим прямоугольник с длиной 8см и шириной 6см. Диагонали этого прямоугольника будут равны 10см.

Если через точку пересечения диагоналей провести перпендикуляры, то они разделят прямоугольник на 8 египетских треугольников.

Перпендикуляр из точки пересечения к шесту указывает на конец складки. Возможно 2 складки наброшенные на руку указывают на необходимость построения 2 диагоналей.

δακτυλος - дактиль (палец)-18,5 мм;

18,5 х7=129,5

Линия МП проходит через глаза учёного и указывает на букву М

М несарх- отец Пифагора. Некоторые считают Мнесарха уроженцем Самоса. Но Клеанф (в V книге “Мифических повествований”) говорит, будто Мнесарх был сириец из сирийского Тира и будто он однажды в неурожайный год приплыл на Самос по торговым делам, устроил раздачу хлеба, и за это был удостоен самосского гражданства. Отец Пифагора был резчик по драгоценным камням.

П арфенис - мать Пифагора, происходила из знатной самоской семьи, ведущей свой род от самого Анкая. Мнесарх под впечатлением пророчества Дельфийской Пифы изменил её имя на Пифазис . Дельфийская Пифа им напророчествовала рождение ребёнка, который превзойдет всех людей в красоте, силе и мудрости

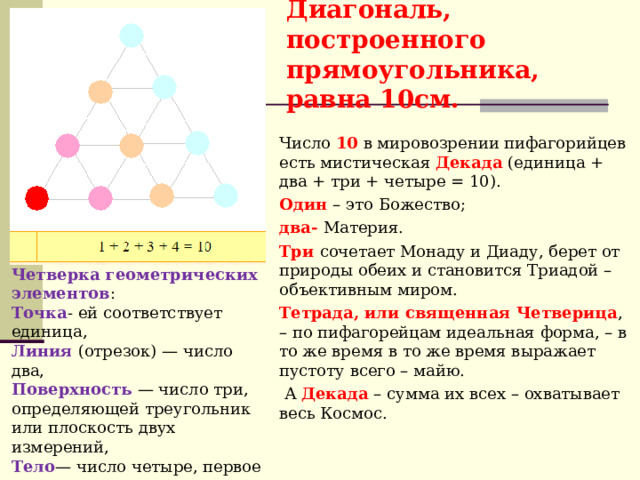
Диагональ, построенного прямоугольника, равна 10см.

Число 10 в мировозрении пифагорийцев есть мистическая Декада (единица + два + три + четыре = 10).

Один – это Божество;

два- Материя.

Три сочетает Монаду и Диаду, берет от природы обеих и становится Триадой – объективным миром.

Тетрада, или священная Четверица , – по пифагорейцам идеальная форма, – в то же время в то же время выражает пустоту всего – майю.

А Декада – сумма их всех – охватывает весь Космос.

Четверка геометрических элементов :

Точка - ей соответствует единица,

Линия (отрезок) — число два,

Поверхность — число три, определяющей треугольник или плоскость двух измерений,

Тело — число четыре, первое пирамидальное число, дающее представление о пространстве трёх измерений

СВЯЩЕННЫЙ ЕГИПЕТСКИЙ ТРЕУГОЛЬНИК

Бог Осирис— это 3 ,

богиня Исида— это 4 ,

а бог Гор — это 5 .

Геометрия и размеры молекулы воды для различных состояний а - для парообразного состояния б - для низшего колебательного уровня в - для уровня, близкого к образованию кристалла льда, соответствует геометрии двух египетских треугольников с соотношением сторон 3 : 4 : 5 г - для состояния льда.

Настенная роспись гробницы Рамзеса VI , на которой фараон изображался гипотенузой правильного прямого треугольника со сторонами, соотносящимися как 3:4:5.

Настенная роспись гробницы Рамзеса IX

АХИЛЕСОВА ПЯТА ПИФАГОРА

Пифагор начинал день с пения одной из песен Гомера. Страсть к поэзии Гомера он пронёс через всю свою жизнь. Как и у одного из героев Одиссеи у него была своя Ахиллесова пята –доказательство теоремы. Возможно с чертежом он познакомился во время своей жизни в Египте .

Трон Изиды- стул невесты

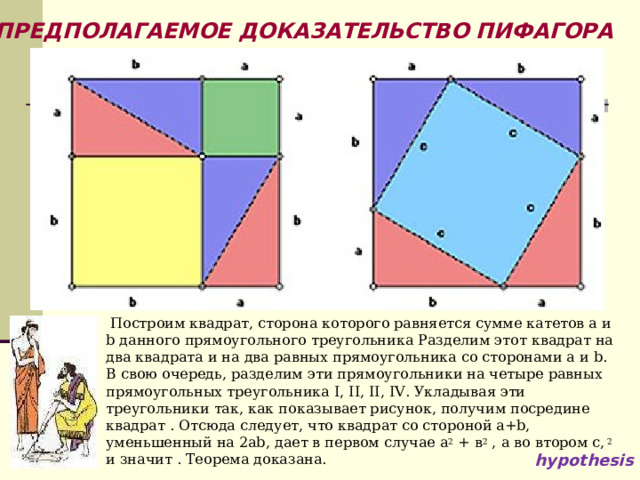
ПРЕДПОЛАГАЕМОЕ ДОКАЗАТЕЛЬСТВО ПИФАГОРА

• Построим квадрат, сторона которого равняется сумме катетов a и b данного прямоугольного треугольника Разделим этот квадрат на два квадрата и на два равных прямоугольника со сторонами a и b. В свою очередь, разделим эти прямоугольники на четыре равных прямоугольных треугольника I, II, II, IV. Укладывая эти треугольники так, как показывает рисунок, получим посредине квадрат . Отсюда следует, что квадрат со стороной a+b, уменьшенный на 2ab, дает в первом случае а 2 + в 2 , а во втором с, 2 и значит . Теорема доказана.

hypothesis

Моя гипотеза

hypothesis

Самоская монета является уменьшенной копией картины пифагорейца. На рисунке он не просто изобразил своего учителя, но и попытался передать основные постулаты его учения, известные для посвящённых.

hypotesis

)

« Если бы нам удалось вступить в контакт с разумными существами какой-нибудь планеты Вселенной, то началась бы эта связь наверняка через теорему Пифагора, потому что она на­столько удивительна и в то же время проста и естественна, что невозможно подумать, чтобы ее не знали и на другой планете».

Джованни Склапарелли (1835 – 1910 )