 Сложение гармонических колебаний. Биения.
Сложение гармонических колебаний. Биения.
Сложение взаимно перпендикулярных колебаний.
Свободные затухающие механические и электромагнитные колебания. Коэффициент затухания.
Логарифмический декремент. Добротность системы.

Метод векторных диаграмм
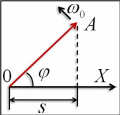 Гармонические колебания изображаются графически методом вращающегося вектора амплитуды или методом векторных диаграмм.
Гармонические колебания изображаются графически методом вращающегося вектора амплитуды или методом векторных диаграмм.
Из произвольной точки О, выбранной на оси х ,
под углом , равным начальной фазе колебания,
откладывается вектор А , модуль которого равен амплитуде А, рассматриваемого колебания. Если этот вектор будет вращаться вокруг точки О с угловой
скоростью , то проекция вектора на ось Х будет
совершать колебания по закону
s Аcos t


Сложение гармонических колебаний
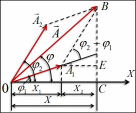 Если система одновременно участвует в нескольких колебательных процессах, то под сложением колебаний понимают нахождение закона, описывающего результирующий колебательный процесс.
Если система одновременно участвует в нескольких колебательных процессах, то под сложением колебаний понимают нахождение закона, описывающего результирующий колебательный процесс.
Для сложения колебаний
х1 и
х2 используем
метод вращающегося вектора амплитуды (метод векторных диаграмм).
х1 А1 cos t 1
х2 А2 cos t 2


Так как векторы
A1 и
A2 вращаются с одинаковой угловой
скоростью , то разность фаз 2 1 между ними
остается постоянной. Уравнение результирующего колебания будет


х х1 х2 А cos t
Где амплитуда
А и начальная фаза
задаются соотношениями:
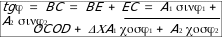 Начальная фаза его определяется из треугольника ОВС:
Начальная фаза его определяется из треугольника ОВС:


Сумма двух гармонических колебаний одного направления и одинаковой частоты есть гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания.
Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний:


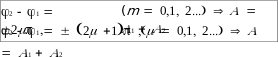

Биения
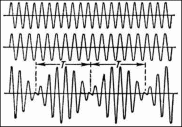
Биениями называются периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний одного направления с близкими частотами.
Пусть амплитуды складываемых колебаний равны A, а частоты равны
и ( ) , причем .
Путь для простоты начало отсчета выбрано так, чтобы начальные фазы
обоих колебаний были равны нулю:

х1 А cost х2 А cos t
x x1 x2 Аcost Аcos t
A cost cos t
2Acos t t cos t t
2 2
2Acos 2t t cos t
2 2
2Acos 2t 0t cos t
2Acos t cost
2 2
2
Результирующее колебание будет иметь вид:
 — гармоническое колебание с частотой , амплитуда
— гармоническое колебание с частотой , амплитуда
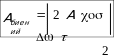 которого изменяется по закону с
которого изменяется по закону с

биений
частотой (частота биений в двое больше
частоты изменения косинуса, поскольку модулю).
Абиений берется по
Сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты


x A cost, y B cos t
Пусть два гармонических колебания одинаковой частоты ω происходят во взаимно перпендикулярных направлениях вдоль осей Х и Y. Для простоты выберем начало отсчета так, чтобы начальная фаза первого колебания была равна нулю:
где
2 1 - разность фаз колебаний, а А и В
— их амплитуды.
 Уравнение траектории результирующего колебания (исключая время t из уравнений) есть уравнение эллипса, произвольно расположенного относительно координатных осей
Уравнение траектории результирующего колебания (исключая время t из уравнений) есть уравнение эллипса, произвольно расположенного относительно координатных осей

Линейно поляризованные колебания
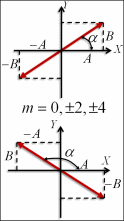 Если разность фаз равна
Если разность фаз равна
m (m 0, 1, 2)
 То эллипс вырождается в отрезок прямой
То эллипс вырождается в отрезок прямой
y B x
A

где знак плюс соответствует нулю и четным
значениям m, а знак минус — нечетным значениям т. Результирующее колебание является гармоническим

 колебанием с частотой и амплитудой и совершается вдоль прямой, составляющей с осью x угол
колебанием с частотой и амплитудой и совершается вдоль прямой, составляющей с осью x угол
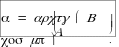
Такие колебания называются линейно
поляризованными колебаниями.

Циркулярно-поляризованные колебания
Если разность фаз равна
2m 1
2
(m 0, 1, 2) , то в данном

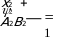 случае уравнение траектории принимает вид:
случае уравнение траектории принимает вид:
Это уравнение эллипса, оси которого совпадают с
осями координат, а его полуоси равны соответствующим амплитудам А и В.
Если А = В то эллипс вырождается в окружность, и такие колебания называются циркулярно - поляризованными или колебаниями, поляризованными по кругу.

Фигуры Лиссажу
Если взаимно перпендикулярные колебания происходят
c циклическими частотами p, q , где p и q — целые
числа:
x
A cos pt ,
y B cos qt
то значения координат x и y одновременно повторяются через одинаковые промежутки времени Т0
равные наименьшему общему кратному периодов T1
2
2
T2 q
колебаний вдоль осей Х и Y.
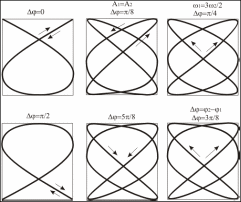
Траектории замкнутых кривых, которые получаются в этих случаях, называются фигурами Лиссажу. Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рисунке 12 показан вид фигур Лиссажу при трех различных значениях отношения
(2:1, 3:2. 4:3) и разности фаз

.
2

Затухающие колебания
Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Затухание механических колебаний вызывается главным образом трением. Затухание в электрических колебательных
системах вызывается тепловыми потерями и потерями на излучение электромагнитных волн, а также тепловыми потерями в диэлектриках и ферромагнетиках вследствие электрического и магнитного гистерезиса.
Закон затухания колебаний определяется свойствами колебательных систем.
Система называется линейной, если параметры, характеризующие те физические свойства системы, которые существенны для рассматриваемого процесса, не изменяются в ходе процесса. Линейные системы описываются линейными дифференциальными уравнениями.
Различные по своей природе линейные системы описываются одинаковыми уравнениями, что позволяет осуществлять единый подход к изучению колебаний различной физической природы.

Дифференциальное уравнение свободных затухающих колебаний линейной системы
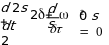 Дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид
Дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид

где S - колеблющаяся величина,
— коэффициент затухания.

0
0 – циклическая частота свободных незатухающих колебаний той же колебательной системы (при
0 )  В случае малых затуханий уравнения:
В случае малых затуханий уравнения:
2 2
решение этого

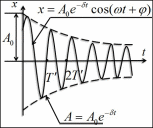 где:
где:
колебаний,
— амплитуда затухающих

A
0 - начальная амплитуда,
– циклическая частота затухающих колебаний.
Промежуток времени в течение, которого амплитуда затухающих колебаний
уменьшается в е раз, называется временем релаксации
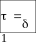

Затухание нарушает периодичность колебаний.
Затухающие колебания не являются периодическими
(апериодические).
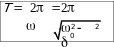 Однако если затухание мало, то можно условно пользоваться понятием периода затухающих колебаний как промежутка времени между двумя последующими максимумами колеблющейся физической величины:
Однако если затухание мало, то можно условно пользоваться понятием периода затухающих колебаний как промежутка времени между двумя последующими максимумами колеблющейся физической величины:

Декремент затухания
Если
A(t ) ,
A(t T )
— амплитуды двух
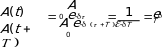 последовательных колебаний, соответствующих моментам времени, отличающихся на период, то отношение
последовательных колебаний, соответствующих моментам времени, отличающихся на период, то отношение


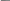
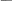 Называется декрементом затухания, а его логарифм
Называется декрементом затухания, а его логарифм
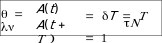
Называется логарифмическим декрементом затухания.
Здесь N – число колебаний, совершаемых за время уменьшения амплитуды в e раз.
Декремент затухания – это количественная характеристика затухающих колебаний в линейной системе.

Добротность колебательной системы
 Добротностью колебательной системы называется безразмерная величина Q равная произведению 2 на отношение энергии W(t) колебаний системы в произвольный момент времени t к убыли этой энергии за промежуток времени от t до t+T (за один условный период затухающих колебаний):
Добротностью колебательной системы называется безразмерная величина Q равная произведению 2 на отношение энергии W(t) колебаний системы в произвольный момент времени t к убыли этой энергии за промежуток времени от t до t+T (за один условный период затухающих колебаний):

А(t)
Энергия W(t) пропорциональна квадрату амплитуды


mA22
W K U
2
,
 поэтому:
поэтому:



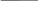
 Поэтому при малых значениях логарифмического
Поэтому при малых значениях логарифмического
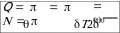 декремента затухания 1 ,
декремента затухания 1 ,
1 e2
2
Добротность — количественная характеристика резонансных свойств колебательной системы, указывающая, во сколько раз амплитуда установившихся вынужденных колебаний при резонансе превышает амплитуду вынужденных колебаний вдали от резонанса, т. е. в области столь низких частот, где амплитуду вынужденных колебаний можно считать не зависящей от частоты.

Примеры свободных затухающих колебаний
Рассмотрим затухающие колебания различной физической природы:
механические колебания — пружинный маятник с массой m, который совершает малые колебания под

F kx
действием упругой силы и силы трения

F rx˙ rv
(
r– коэффициент сопротивления).
электромагнитные колебания — колебания в колебательном контуре, состоящем из сопротивления R индуктивности L и емкости C.
Причиной затухания колебаний в электрическом колебательном контуре является превращение части энергии

dQ = I 2 Rdt
тока в джоулево тепло на омическом сопротивлении
R 
и рассеянии этого тепла в окружающую среду.










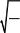

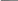
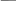







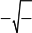 Электрических колебаний в контуре не возникает, если его омическое сопротивление R велико, или очень мала индуктивность L контура, или слишком велика его емкость С, т.е. если выполнено условие
Электрических колебаний в контуре не возникает, если его омическое сопротивление R велико, или очень мала индуктивность L контура, или слишком велика его емкость С, т.е. если выполнено условие
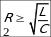
Будем сравнивать оба случая с дифференциальным
уравнением свободных затухающих колебаний линейной системы
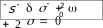

 или
или
Решением этого уравнения является выражение
|
| s A e t cos(t ) 0 |
|
|
| Пружинный маятник | Колебательный контур |
| Колеблющаяся величина | Смещение относительно положения равновесия x | Заряд q |
| Дифференциально е уравнение колебаний | ˙x˙ r x˙ m d 2 х r dt 2 m | m dх k х 0 dt m | q˙˙ R q˙ 1 q 0 L LC d 2q R dq 1 dt2 L dt LC q |
0 |
| Собственная частота незатухающих | 0 | k m | 1 0 LC |
| колебаний 0 |
|
| Коэффициент затухания | r 2m | R 2L |
| Частота | | k r2 m 4m2 | 2 1 R 0 LC 4L2 |
| затухающих |
| колебаний |
| 2 2 |
|
| 0 |
|
Добротность Q Q 0 2 |
Q |
km r | Q 1 L R C |

| Амплитуда колебаний | А A e t 0 A0 максимальная амплитуда | q q et 0 q0 максимальный заряд |
| Закон колебаний | x A e t cos(t ) 0 | q q e t cos(t ) 0 |



2







 Сложение гармонических колебаний. Биения.
Сложение гармонических колебаний. Биения.
 Гармонические колебания изображаются графически методом вращающегося вектора амплитуды или методом векторных диаграмм.
Гармонические колебания изображаются графически методом вращающегося вектора амплитуды или методом векторных диаграмм.

 Если система одновременно участвует в нескольких колебательных процессах, то под сложением колебаний понимают нахождение закона, описывающего результирующий колебательный процесс.
Если система одновременно участвует в нескольких колебательных процессах, то под сложением колебаний понимают нахождение закона, описывающего результирующий колебательный процесс.



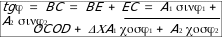 Начальная фаза его определяется из треугольника ОВС:
Начальная фаза его определяется из треугольника ОВС:


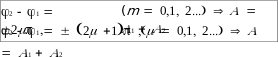

 Биениями называются периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний одного направления с близкими частотами.
Биениями называются периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний одного направления с близкими частотами. 
 — гармоническое колебание с частотой , амплитуда
— гармоническое колебание с частотой , амплитуда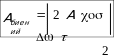 которого изменяется по закону с
которого изменяется по закону с


 Уравнение траектории результирующего колебания (исключая время t из уравнений) есть уравнение эллипса, произвольно расположенного относительно координатных осей
Уравнение траектории результирующего колебания (исключая время t из уравнений) есть уравнение эллипса, произвольно расположенного относительно координатных осей Если разность фаз равна
Если разность фаз равна То эллипс вырождается в отрезок прямой
То эллипс вырождается в отрезок прямой

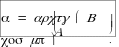

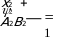 случае уравнение траектории принимает вид:
случае уравнение траектории принимает вид:

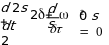 Дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид
Дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид

 В случае малых затуханий уравнения:
В случае малых затуханий уравнения:
 где:
где: A0 - начальная амплитуда,
A0 - начальная амплитуда, 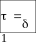
 Затухание нарушает периодичность колебаний.
Затухание нарушает периодичность колебаний. 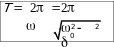 Однако если затухание мало, то можно условно пользоваться понятием периода затухающих колебаний как промежутка времени между двумя последующими максимумами колеблющейся физической величины:
Однако если затухание мало, то можно условно пользоваться понятием периода затухающих колебаний как промежутка времени между двумя последующими максимумами колеблющейся физической величины: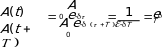 последовательных колебаний, соответствующих моментам времени, отличающихся на период, то отношение
последовательных колебаний, соответствующих моментам времени, отличающихся на период, то отношение

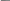
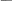 Называется декрементом затухания, а его логарифм
Называется декрементом затухания, а его логарифм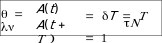
 Добротностью колебательной системы называется безразмерная величина Q равная произведению 2 на отношение энергии W(t) колебаний системы в произвольный момент времени t к убыли этой энергии за промежуток времени от t до t+T (за один условный период затухающих колебаний):
Добротностью колебательной системы называется безразмерная величина Q равная произведению 2 на отношение энергии W(t) колебаний системы в произвольный момент времени t к убыли этой энергии за промежуток времени от t до t+T (за один условный период затухающих колебаний):
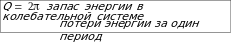


 поэтому:
поэтому:


 Поэтому при малых значениях логарифмического
Поэтому при малых значениях логарифмического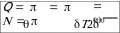 декремента затухания 1 ,
декремента затухания 1 ,








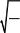








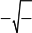 Электрических колебаний в контуре не возникает, если его омическое сопротивление R велико, или очень мала индуктивность L контура, или слишком велика его емкость С, т.е. если выполнено условие
Электрических колебаний в контуре не возникает, если его омическое сопротивление R велико, или очень мала индуктивность L контура, или слишком велика его емкость С, т.е. если выполнено условие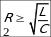
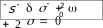

 или
или




















