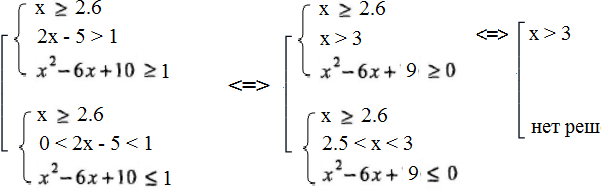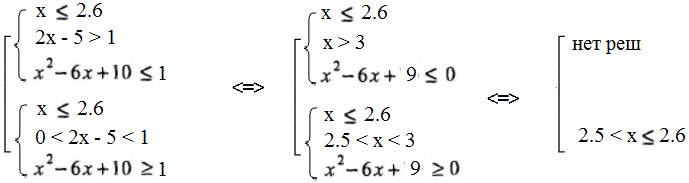Муниципальное бюджетное общеобразовательное учреждение
«Благодарновская средняя общеобразовательная школа»
Методическая разработка
урока по алгебре в 11 –м классе по теме:
Решение логарифмических неравенств
Подготовила:
Учитель математики
МБОУ «Благодарновская СОШ»
Тухватуллина Елена Александровна
2023г.
Ключём к решению логарифмических неравенств являются свойства логарифмической функции. Эти свойства следует знать!
 1. Область определения:
1. Область определения: 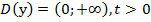 ;
;
2. Область значений: 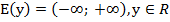 ;
;
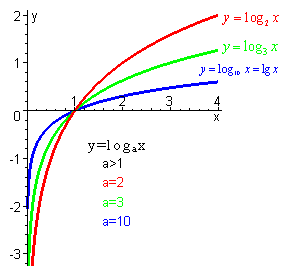
3. При 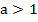 монотонно возрастает, т.е. если t2 t1, то log a t2 log a t1 При
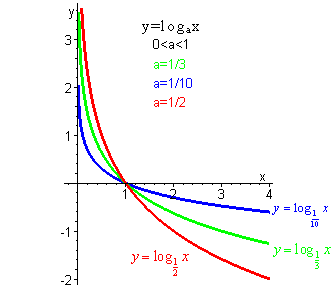
монотонно возрастает, т.е. если t2 t1, то log a t2 log a t1 При 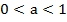 монотонно убывает, т.е. если t2 t1 то log a t2 log a t1.
монотонно убывает, т.е. если t2 t1 то log a t2 log a t1.
Именно монотонность логарифмической функции позволяет решать простейшие логарифмические неравенства.
Рассмотрим решение логарифмического неравенства, когда основание логарифма а 1.
Неравенство необходимо решать, применяя равносильные преобразования. Вот схема. 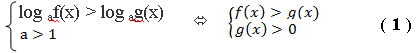 Как эта система получилась? По условию logaf(x) logag(x) Мы знаем что, при а 1 функция монотонно возрастает. Отсюда: f(x) g(x). (1-ая строка системы)
Как эта система получилась? По условию logaf(x) logag(x) Мы знаем что, при а 1 функция монотонно возрастает. Отсюда: f(x) g(x). (1-ая строка системы)
При этом необходимо не забыть про ОДЗ, т. к. под логарифмом могут стоять строго положительные выражения. ОДЗ представляется системой:
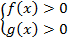 Учитывая
Учитывая 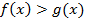 , для соблюдения ОДЗ достаточно защитить меньшее из чисел. Получаем исходное неравенство равносильно системе.
, для соблюдения ОДЗ достаточно защитить меньшее из чисел. Получаем исходное неравенство равносильно системе.
Итак вместо логарифмического неравенства будем решать простое неравенство (линейное, квадратное и т. д.), т.е. освободились от знака loga.
Пример 1. Решить неравенство log2(2х + 2) log2 x. Решение. Основания одинаковые и больше 1.По схеме ( 1) получаем: первый аргумент больше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее из них неравенством больше нуля. 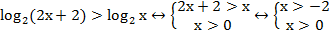

Ответ: 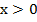
Рассмотрим логарифмическое неравенство, когда основание логарифма 0a , т.е. 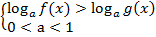
Поскольку 0a. Отсюда:
logaf(x) logag(x) = f(x)
При этом необходимо не забыть про ОДЗ, т. к. под логарифмом могут стоять строго положительные выражения. ОДЗ представляется системой 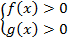
Учитывая f(x) g(x), для соблюдения ОДЗ достаточно защитить меньшее из чисел. Получаем, исходное неравенство равносильно системе: 
Пример 2. Решить неравенство: 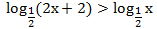 Решение. Основания одинаковые и меньше 1.По схеме (2) получаем: первый аргумент меньше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее из них.
Решение. Основания одинаковые и меньше 1.По схеме (2) получаем: первый аргумент меньше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее из них.
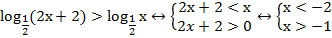

Ответ: нет решений
Все остальные более сложные логарифмические неравенства сводятся к простейшим.
Алгоритм решения:
1. Уравнять основания логарифмов;
2. Сравнить подлогарифмические выражения:
- при 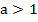 сохранить знак неравенства;
сохранить знак неравенства;
- при 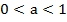 изменить знак неравенства на противоположный;
изменить знак неравенства на противоположный;
3. Учесть ОДЗ.
Пример 3. Решите неравенство: 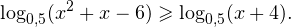
Решение. Основания логарифмов равны и меньше единицы, По схеме (2) получаем: первый аргумент меньше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее из них. Имеем систему 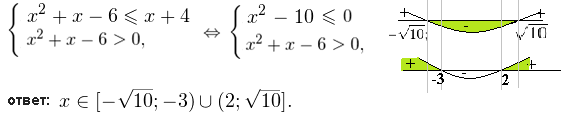
Пример 4. Решить неравенство: 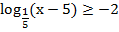 Решение. В левой части log , а в правой число. Приведем к виду logaf(x) ≥ logag(x). Для этого число в правой части представим в виде логарифма с тем же основанием, что логарифм в левой части, т.е.
Решение. В левой части log , а в правой число. Приведем к виду logaf(x) ≥ logag(x). Для этого число в правой части представим в виде логарифма с тем же основанием, что логарифм в левой части, т.е.
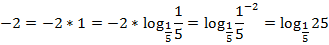 применили
применили 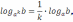
Итак, имеем неравенство: 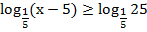
Основание логарифмов равны и меньше единицы, По схеме (2) получаем: первый аргумент меньше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее. Имеем систему:

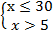
 Ответ:
Ответ: 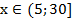
Пример 5. Решить неравенство log8(x2-4x+3). Решение. В левой части log8t , а в правой 1. Приведем к виду logaf(x) logag(x). Представим 1 в виде логарифма с тем же основанием, что логарифм в правой части, т.е. 1 = log88, тогда неравенство примет вид: log8(x2 – 4x + 3) log88. Основание логарифмов равны и больше единицы, По схеме (1) получаем: первый аргумент меньше второго, по ОДЗ оба они больше нуля. Так как мы защищаем меньшее, то получим систему: 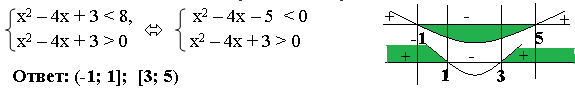
Логарифмические неравенства, сводящиеся к простейшим
Более сложные логарифмические неравенства сводятся к простейшим методами, аналогичными используемым при решении логарифмических уравнений.
Пример 1. Решить неравенство: 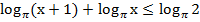
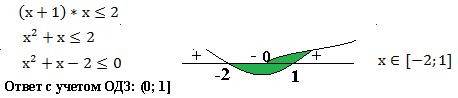
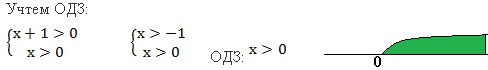 Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:
Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:
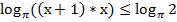
Нам известно, что число 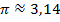 . Поэтому в равносильном неравенстве знак исходного неравенства сохраняется.
. Поэтому в равносильном неравенстве знак исходного неравенства сохраняется.
Пример 2. Решить неравенство: 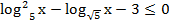
Решение: ОДЗ: х 0. Видим два логарифма, но с разными основаниями. Приведем второй член к основанию 5. Получили неравенство:
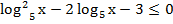 Очевидна замена:
Очевидна замена: 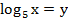
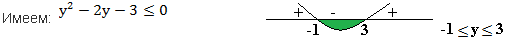 Вернемся к исходным переменным:
Вернемся к исходным переменным:
-1 ≤ log5 x ≤ 3 . -1* -log55 ≤ log5 x ≤ 3* log55
log55-1 ≤ log5 x ≤ log553 
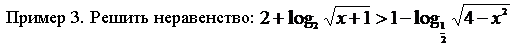 Решение. Преобразуем к простейшему логарифмическому неравенству. Видим два логарифма, основания разные; и в левой и в правой части есть числа. Перейдем к основанию 2 в выражении, стоящем в правой части данного неравенства, а числа запишем в виде логарифма:
Решение. Преобразуем к простейшему логарифмическому неравенству. Видим два логарифма, основания разные; и в левой и в правой части есть числа. Перейдем к основанию 2 в выражении, стоящем в правой части данного неравенства, а числа запишем в виде логарифма: 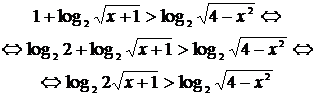 Основания одинаковые и больше 1.Функция log2 t – возрастающая, поэтому первый аргумент больше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее. Теперь перейдем к равносильной системе:
Основания одинаковые и больше 1.Функция log2 t – возрастающая, поэтому первый аргумент больше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее. Теперь перейдем к равносильной системе:
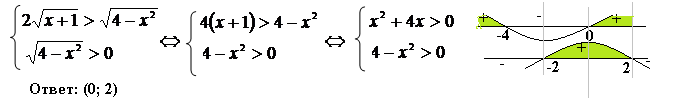
Если в неравенстве встречается логарифмическая функция, содержащая неизвестное в основании, то, как правило, следует рассматривать два случая: 1) когда основание больше 1, 2) когда основание положительно, но меньше 1.
Пример 4. Решить неравенство log x–3(x2-4x+3).
Решение. Преобразуем правую часть в логарифм с требуемым основанием: 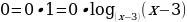 =
=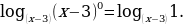 Имеем неравенство:
Имеем неравенство:
log x–3(x2 – 4x + 3) x–31. (простейшее неравенство) Так как основание логарифма содержит переменную, то рассмотрим два случая x-31 и 0x-3. Если основание логарифма больше 1, то функция – возрастающая, поэтому первый аргумент меньше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее. Теперь перейдем к равносильной системе:
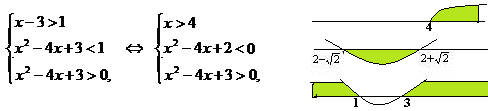 Совмещаем промежутки и видим, что данная система не имеет решений.
Совмещаем промежутки и видим, что данная система не имеет решений.
Рассмотрим второй случай, если 0 . Функция log(x-3)t – убывающая, поэтому, знак неравенства меняется. Для соблюдения ОДЗ достаточно защитить меньшее из аргументов. В этом случае получаем систему:
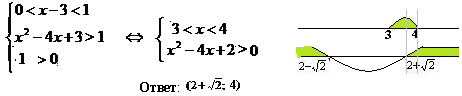
Пример 5. Решить неравенство 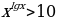
Решение. ОДЗ: х 0. Так как выражения, стоящие в левой и правой частях неравенства положительны, то для решения прологарифмируем обе части по основанию 10. Получим равносильное исходному неравенство:
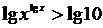 , пользуясь свойствами логарифмов lgx * lgx 1
, пользуясь свойствами логарифмов lgx * lgx 1
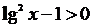 . Обозначим t = lg x и решим неравенство: .
. Обозначим t = lg x и решим неравенство: . 
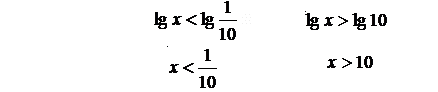
Учитывая ОДЗ х 0  Ответ: (0; 0,1)(10;+).
Ответ: (0; 0,1)(10;+).
Пример 6. Решить неравенство 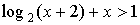
Решение. ОДЗ: х -2. Если привести к простейшему виду logaf(x) logag(x) не получим облегченного неравенства. Попробуем записать в виде:
log2(x + 2) -x + 1. Это логарифмическо-линейное неравенство. Можно попробовать графический метод. Лучше использовать монотонность функции. В левой части монотонно возрастающая функция: f(x) = log2(x + 2), а в правой – монотонно убывающая: g(x) = -x + 1. Значит уравнение log2(x + 2) = -x + 1 имеет не более одного корня. Подбором находим что х = 0 есть корень этого уравнения . Проверим f(2)=2, a g(2)= -1. Значит правее х = 1 функция f(x) = log2(x + 2) больше чем g(x) = -x + 1. Ответ: х 1.
Пример 7. Решите неравенство 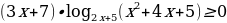
Решение. ОДЗ: 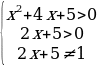
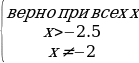
Очень часто бывает довольно несложное неравенство обычными преобразованиями трудно решить. Вот в таких случаях нам помогает универсальный метод - метод интервалов.
Нам надо избавиться от переменного основания, так как знак логарифмического выражения зависит как от аргумента, так и от основания. Пусть перейдем к основанию 2. Тогда имеем 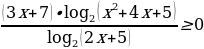 . Оно равносильно неравенству
. Оно равносильно неравенству
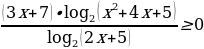
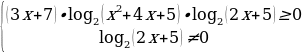
Рассмотрим функцию y = (3x + 7)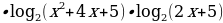
Находим нули функции:
3x + 7 = 0 или 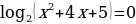
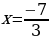 или
или 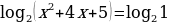
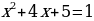
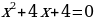
(x + 2)2 = 0
x = -2 (кратность равна 2)
Второе неравенство дает 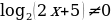
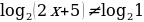
2x + 5 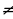 1 x
1 x 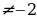 .
.
Видим х = -2 имеет кратность 3. Нули функции отметим на координатной прямой. Учитывая кратность нулей методом «тыка» находим знак функции.
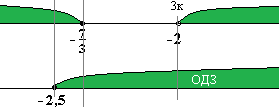 Ответ:
Ответ: 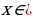
У метода интервалов есть свои минусы. Потому что не всегда удобно определять знаки на промежутках, тем более когда они малы, когда на них нет целых значений.
Пример 8. Решите неравенство 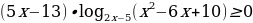
Решение. В этом случае применим метод равносильных преобразований. Это неравенство равносильно совокупности двух систем:
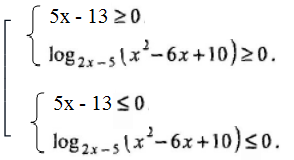
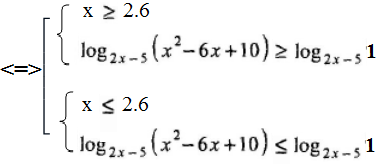 Первая система равносильно совокупности двух систем:
Первая система равносильно совокупности двух систем:
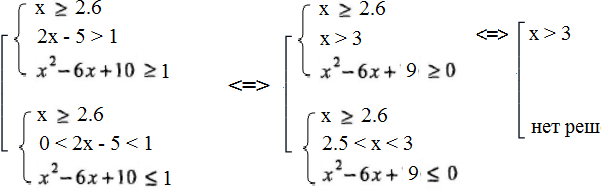
Итак решением первой системы будет промежуток (3 ;  ).
).
Также вторая система равносильно совокупности двух систем:
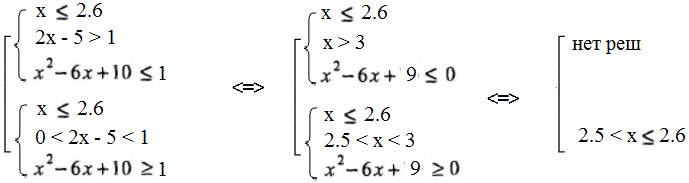
Решением второй системы будет промежуток 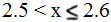
Таким образом, решением исходного неравенства 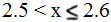 ; x 3.
; x 3.
Ответ. (2,5; 2,6]; (3;  )
)








 1. Область определения:
1. Область определения: 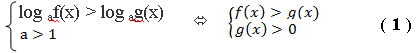 Как эта система получилась? По условию logaf(x) logag(x) Мы знаем что, при а 1 функция монотонно возрастает. Отсюда: f(x) g(x). (1-ая строка системы)
Как эта система получилась? По условию logaf(x) logag(x) Мы знаем что, при а 1 функция монотонно возрастает. Отсюда: f(x) g(x). (1-ая строка системы) 
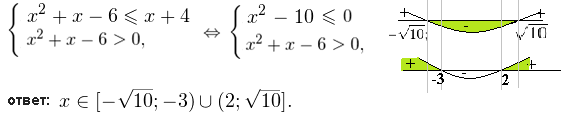
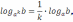
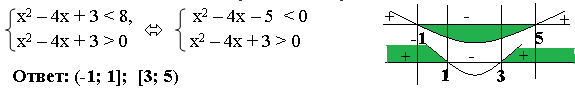
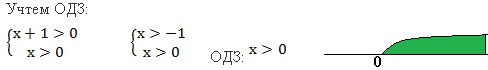 Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:
Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:

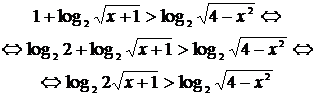 Основания одинаковые и больше 1.Функция log2 t – возрастающая, поэтому первый аргумент больше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее. Теперь перейдем к равносильной системе:
Основания одинаковые и больше 1.Функция log2 t – возрастающая, поэтому первый аргумент больше второго, по ОДЗ оба они больше нуля. Для соблюдения ОДЗ достаточно защитить меньшее. Теперь перейдем к равносильной системе: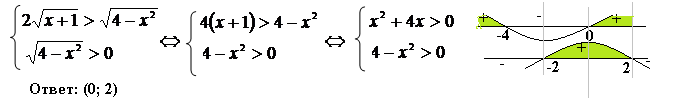
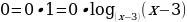 =
=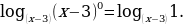 Имеем неравенство:
Имеем неравенство: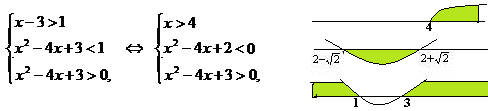 Совмещаем промежутки и видим, что данная система не имеет решений.
Совмещаем промежутки и видим, что данная система не имеет решений.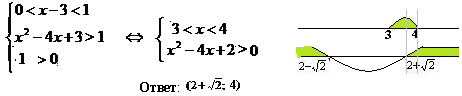
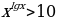

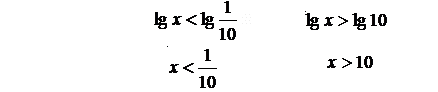
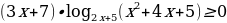
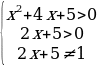
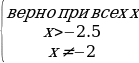
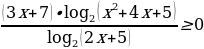 . Оно равносильно неравенству
. Оно равносильно неравенству 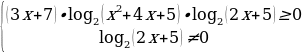
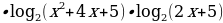
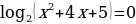
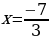 или
или 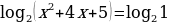
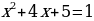
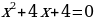
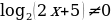
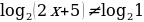
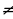 1 x
1 x 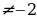 .
. Ответ:
Ответ: 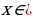
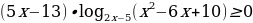
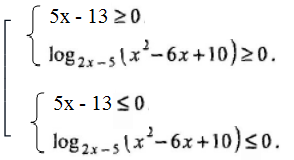
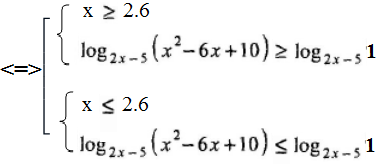 Первая система равносильно совокупности двух систем:
Первая система равносильно совокупности двух систем: