Презентация " Прямая Эйлера"

ПРЯМАЯ ЭЙЛЕРА

Подготовили: Кошкаров В, Белова Е,

Привезенцев Н,

Учитель: Козлова О. Е.

ГБОУ СОШ № 15 г. Севастополь

Эйлер как великий математик XVIII ст.

Леонард Эйлер — швейцарский, немецкий и российский математик и механик, внёсший фундаментальный вклад в развитие этих наук. Эйлер оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Познания Эйлера были энциклопедичны; кроме математики, он глубоко изучал ботанику, медицину, химию, теорию музыки, множество европейских и древних языков.

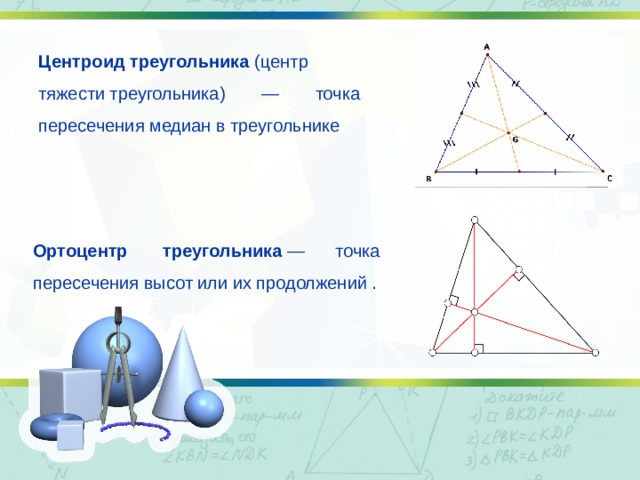
Центроид   треугольника  (центр тяжести треугольника) — точка пересечения медиан в треугольнике

Ортоцентр   треугольника  — точка пересечения высот или их продолжений .

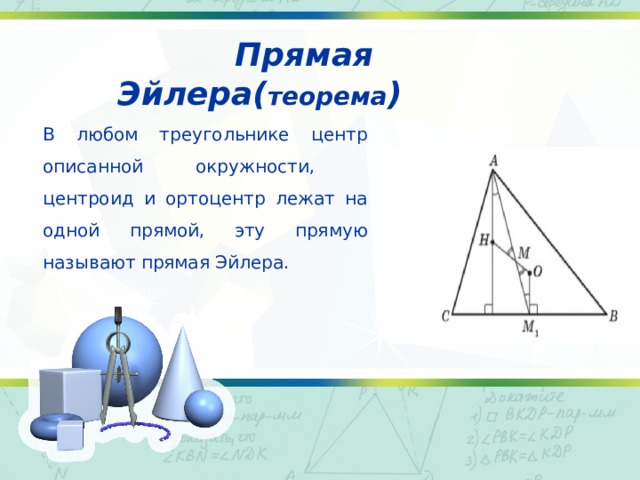
Прямая Эйлера( теорема )

В любом треугольнике центр описанной окружности, центроид и ортоцентр лежат на одной прямой, эту прямую называют прямая Эйлера.

треугольники HAM и OMM 1 (подобны по двум углам) = AM/MM 1 = AH/OM 1 =2 3) Итак, точка M делит медиану AM 1 в отношении 2:1, считая от вершины A. Отсюда точка M - центроид треугольника ABC = HM = 2MO. Точки O, M и H лежат на одной прямой. ч. т. д.   " width="640"

Доказательство теоремы Эйлера

1) Так как точка M 1 - середина стороны BC, то отрезок AM 1 - медиана треугольника ABC.

2) Пусть M - точка пересечения отрезков A M 1 и OH. Так как AH||OM 1 , то ∠HAM = ∠OM 1 M. Углы AMH и M 1 MO равны (вертикальные) = треугольники HAM и OMM 1 (подобны по двум углам) =

AM/MM 1 = AH/OM 1 =2

3) Итак, точка M делит медиану AM 1 в отношении 2:1, считая от вершины A. Отсюда точка M - центроид треугольника ABC = HM = 2MO. Точки O, M и H лежат на одной прямой.

ч. т. д.  

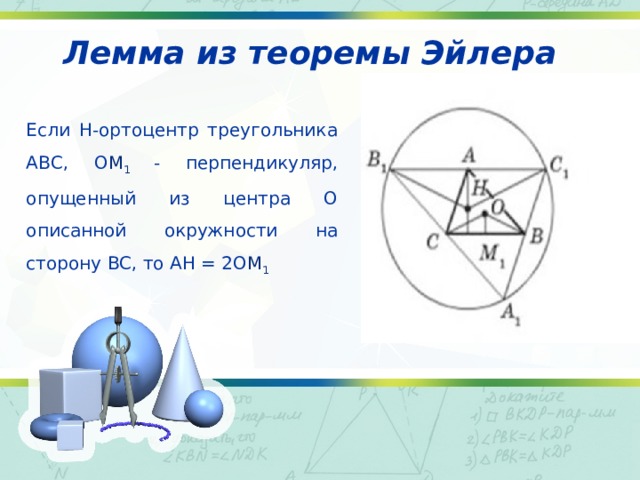
Лемма из теоремы Эйлера

Если H-ортоцентр треугольника ABC, O M 1 - перпендикуляр, опущенный из центра O описанной окружности на сторону BC, то AH = 2O M 1

Доказательство леммы из теоремы Эйлера

1) Через каждую высоту треугольника ABC проведем прямую, параллельную противолежащей стороне. Получим треугольник A 1 B 1 C 1

2) Так как два угла опираются на одну и ту же дугу, то

∠ B 1 HC 1 = 2∠B 1 A 1 C 1 . Углы BAC и B 1 A 1 C 1 равны как противолежащие углы параллелограмма ABA 1 C, поэтому

∠ BOC = 2∠BAC=2∠B 1 A 1 C 1 = ∠B 1 HC 1 .

3) Так как B 1 C 1 =2BC, то равнобедренные треугольники COB и B 1 HC 1 подобны с коэффициентом подобия 2

4) Так как отрезок AH и OM 1 - соответственны высотам подобных треугольников, то AH = 2OM 1 .

    Что и требовалось доказать: AH = 2OM 1

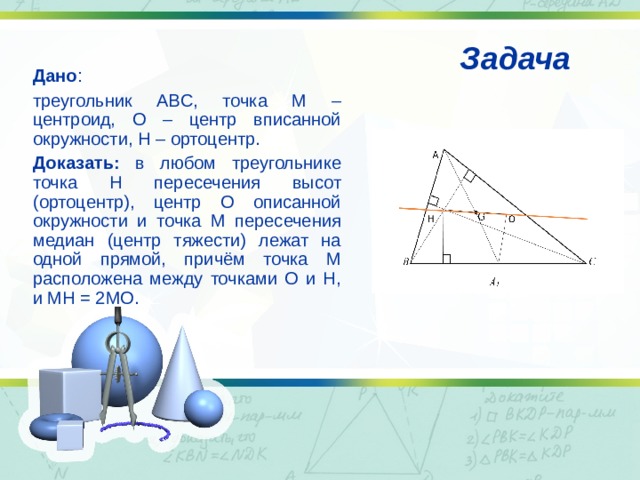
Задача

Дано :

треугольник ABC, точка M – центроид, O – центр вписанной окружности, H – ортоцентр.

Доказать: в любом треугольнике точка H пересечения высот (ортоцентр), центр O описанной окружности и точка M пересечения медиан (центр тяжести) лежат на одной прямой, причём точка M расположена между точками O и H, и MH = 2MO.

Доказательство

1. Пусть A 1 — середина стороны BC треугольника ABC,

G — точка пересечения прямых AA 1 и OH, то по теореме

Эйлера AH = 2OA 1

2. Из подобия треугольников A 1 GO и AGH следует, что

AG/G A 1 = HG/GO = AH/O A 1 = 2

3. Следовательно, G — точка пересечения медиан треугольника

ABC , т.е. G совпадает с M и MH = 2MO

Что и требовалось доказать: MH= 2MO

Литература

1. Геометрия для общеобразовательных учреждений с углубленны: учеб. для 8 кл. / А.Г. Мерзляк, В.Б Полонский, М.C Якир. – М. : «Вентана – Граф», 2016.

2. Задачи по планиметрии: В.B Просолов. – M.:  МЦНМО , 2001. - [Электронный ресурс]. – Режим доступа : https :// math . ru / lib / book / pdf / planim 4. pdf

3. Сборник задач по геометрии: И.B Яковлев. – 

[Электронный ресурс]. – Режим доступа : http:// mathus.ru/math/okr9t.pdf