Презентация к работе "Метод мажорант"

XI научно-практическая конференция «Грани творчества»

«Свойства функции в решении уравнений»

Работа ученика 11 класса Муниципального бюджетного

общеобразовательного учреждения «Гимназия» Дударева Даниила

Научный руководитель – учитель математики МБОУ «Гимназия» Терехова Надежда Анатольевна 2015 год

Цель работы:

Научиться применять свойства функций при решении комбинированных уравнений

Задачи:

• изложить теоретический материал по свойствам функций;
• научиться решать уравнения из вариантов ЕГЭ с использованием свойства монотонности, ограниченности и чётности.
• в помощь учителю создать приложение, в которое будет входить подборка разных задач ;

Гипотеза

возможно ли научится видеть

применение свойств функций при

решении уравнений?

Объект исследования

комбинированные

уравнения

Метод мажорант

К 11 классу мы с одноклассниками решили сотни различных уравнений и неравенств. Исследуя различные способы их решения, я пришла к выводу, что наиболее красивым, наиболее универсальным способом поиска решений является именно этот метод. Очень возможно, что кто-то из вас и не слышал такое выражение, как «метод мажорант».

На самом деле, вы встречались с этим методом, просто не знали, как он называется. Некоторые математики называют этот метод по-другому: «метод математической оценки», «метод mini-max ». Это очень красивый метод, и ему непременно надо научить всех.

Суть метода мажорант:

Способы нахождения мажоранты

• С помощью производной;
• С использованием ограниченности функций;
• С использованием неравенства Коши;
• С использованием множества значений показательной, тригонометрических, квадратичных функций:

Свойство монотонности функции

Практическая часть:

• Решение уравнений;
• Решение неравенств;
• Задания для самостоятельного решения.

Решение уравнений:

1

2

3

6

7

Решение неравенств:

2

3

Выводы:

Метод мажорант применяется к

комбинированному уравнению, если оно

содержит:

1. Тригонометрические и им обратные функции:

2. Квадратичную функцию

3. Показательную функцию

4. Сумму взаимно обратных функций;

5. Иррациональные функции.

Тест для проверки :

Найдём ОДЗ уравнения: R

Оценим левую и правую части уравнения

с использованием множества значений.

В данном уравнении мажоранта равна 1.

Сведём данное уравнение к системе:

Решая второе уравнение и подставляя найденный корень во второе, получим, что уравнение имеет единственный корень х = 0.

Прежде, чем производить оценку, преобразуем

уравнение, используя формулу разности

квадратов и правило выделения полного

квадрата. Тогда

Оценка выполняется с использованием

множества значений функций.

Мажоранта равна 3, а корень уравнения х = -1,2

В данном уравнении оценку правой части произведём с помощью производной

В левой части , учитываем множество

значений функции

+

-

- 0,2

Таким образом, мы показали, что левая часть уравнения при любом х строго меньше правой части,

т.е. уравнение решений не имеет.

При нахождении мажоранты в этом

уравнении, для оценки правой части

используем оценку суммы двух взаимно

обратных функций. Т.к.

то или .

Левая часть оценивается через множество значений:

Т.о. мажорантами являются числа 2

или – 2, тогда уравнение имеет решение:

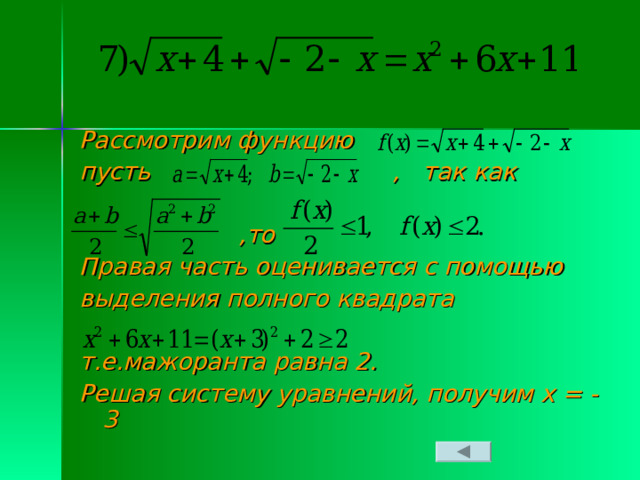
Рассмотрим функцию

пусть , так как

,то

Правая часть оценивается с помощью

выделения полного квадрата

т.е.мажоранта равна 2.

Решая систему уравнений, получим х = -3

Остановлюсь на решении 2 и 3 неравенств.

ОДЗ неравенства: R

Оценим каждый множитель:

т.к показательная функция с основанием большим 1

возрастает.

т.к. логарифмическая функция с основанием

меньшим 1 - убывает.

Т.о. при умножении двух чисел меньших 3 никогда не

получится число большее 9, а вот равное 9 получится

может т.т.т, когда

Ответ: 0

Найдём область допустимых значений неравенства

При любом х из ОДЗ

По определению арифметического корня

тогда

при всех значениях х.

Ответ:

следовательно, в силу свойства суммы взаимно обратных положительных функций, получим: