Преобразование подобия

ПРЕОБРАЗОВАНИЕ

ПОДОБИЯ

ГУ ЛНР «ЛОУ СОШ №41»

Виденеева Н.Н.

Определения слова подобие:

  Нечто похожее, сходное с чем-либо, напоминающее собою что-либо.

• В этой конурке он приладил к стене узенькую трехногую кровать, накрыв ее небольшим подобием тюфяка, убитым и плоским, как блин, и, может быть, так же замаслившимся, как блин, который удалось ему вытребовать у хозяина гостиницы.
• В этой конурке он приладил к стене узенькую трехногую кровать, накрыв ее небольшим подобием тюфяка, убитым и плоским, как блин, и, может быть, так же замаслившимся, как блин, который удалось ему вытребовать у хозяина гостиницы.

• Он показал на середину плаца, где стояло сделанное из сырой глины чучело, представлявшее некоторое подобие человеческой фигуры, только без рук и без ног.
• Он показал на середину плаца, где стояло сделанное из сырой глины чучело, представлявшее некоторое подобие человеческой фигуры, только без рук и без ног.

• У изголовья - столик из дощечки и кольев; на дощечке - подобие шкатулки, а в ней все добро, все хозяйство Таганка; моток ниток, варежки, тавлинка из бересты с нюхательным табаком…
• У изголовья - столик из дощечки и кольев; на дощечке - подобие шкатулки, а в ней все добро, все хозяйство Таганка; моток ниток, варежки, тавлинка из бересты с нюхательным табаком…

• Я решил, что если ближайший день не переменит всей этой злобной нечистоты в хотя бы подобие спокойной жизни, - самое лучшее для меня будет высадиться на первой же остановке.
• Я решил, что если ближайший день не переменит всей этой злобной нечистоты в хотя бы подобие спокойной жизни, - самое лучшее для меня будет высадиться на первой же остановке.

Определения слова подобие в математике:

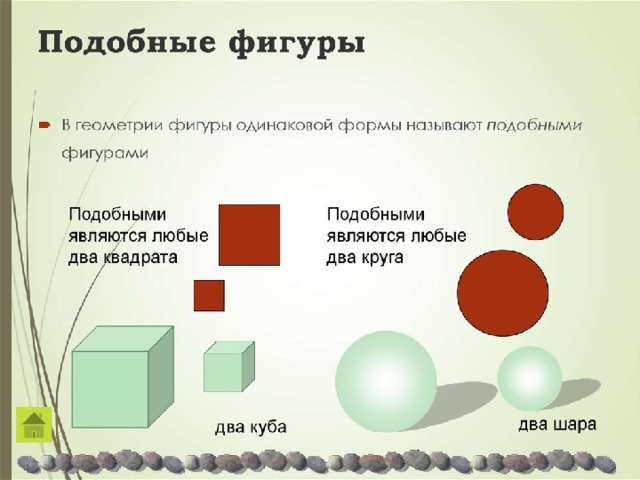
Подобие – это понятие, характеризующее наличие одинаковой, не зависящей от размеров, формы у геометрических фигур.

Подобные фигуры – это фигуры, для которых существует взаимно-однозначное соответствие, при котором расстояние между любыми парами их соответствующих точек изменяется в одно и то же число раз.

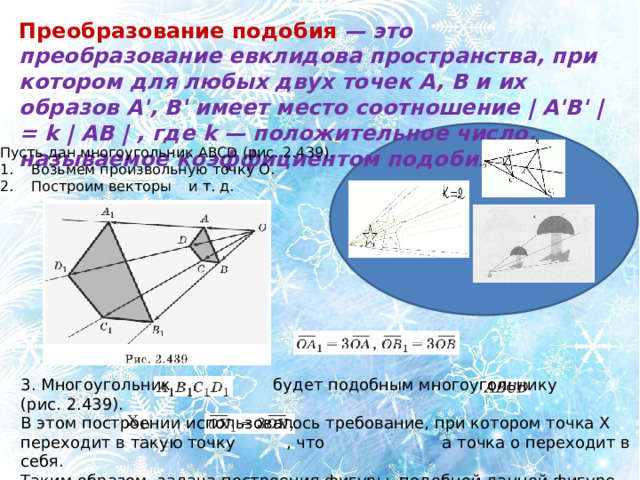
Преобразование подобия   — это преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A', B' имеет место соотношение | A'B' | = k | AB | , где k — положительное число, называемое коэффициентом подобия.

Пусть дан многоугольник ABCD (рис. 2.439).

1.    Возьмем произвольную точку О.

2.    Построим векторы   и т. д.

3. Многоугольник    будет подобным многоугольнику    (рис. 2.439).

В этом построении использовалось требование, при котором точка X переходит в такую точку  , что  а точка о переходит в себя.

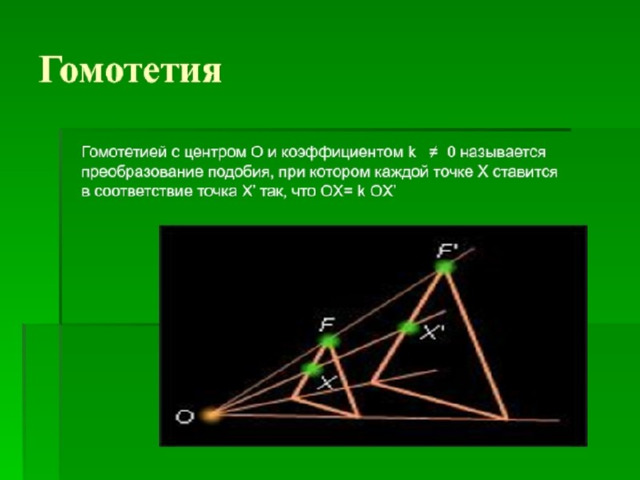
Таким образом, задача построения фигуры, подобной данной фигуре, приводит к новому виду преобразований, которое называют  гомотетией .

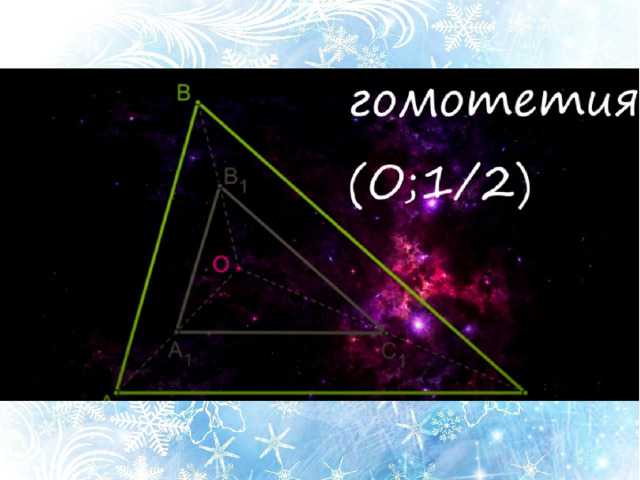
0 , то гомотетичные фигуры располагаются по одну сторону от центра гомотетии (рис. 2.440, 2.441). Если k , то гомотетичные фигуры располагаются по разные стороны от центра гомотетии (рис. 2.442). " width="640"

Определение:  

Гомотетией с центром O и коэффициентом  называют преобразование, при котором каждая точка X переходит в точку , такую, что 

Если при гомотетии фигура  переходит в фигуру , то эти фигуры называют  гомотетичными .

Если k = 1 , то каждая точка X перейдет сама в себя.

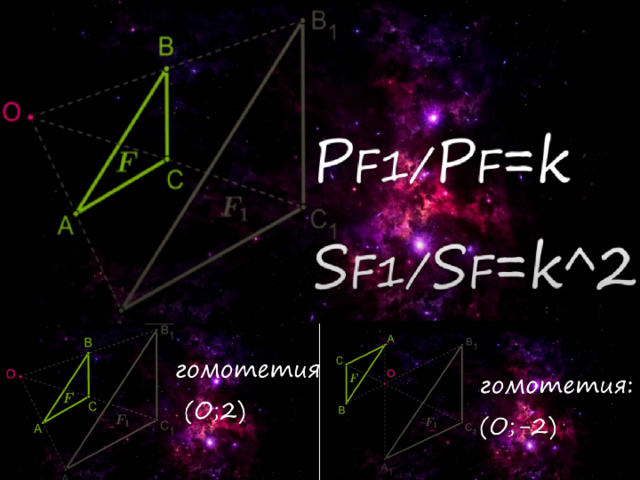
Если k 0 , то гомотетичные фигуры располагаются по одну сторону от центра гомотетии (рис. 2.440, 2.441).

Если k , то гомотетичные фигуры располагаются по разные стороны от центра гомотетии (рис. 2.442).

0 (рис. 2.440), то точки X и  лежат на прямой ОХ по одну сторону от центра гомотетии (так, векторы  сонаправлены). 3)    Если k (рис. 2.442), то точки X и  лежат на прямой ОХ по разные стороны от центра гомотетии (так, векторы  противоположно направлены). Имеет место теорема (смотри следующий слайд). " width="640"

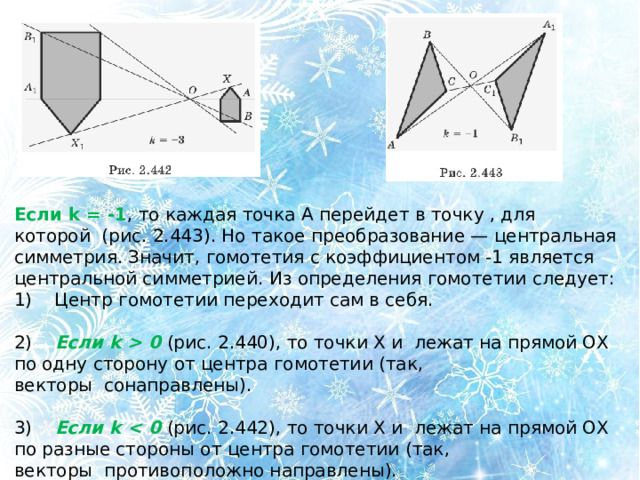
Если k = -1 , то каждая точка А перейдет в точку , для которой  (рис. 2.443). Но такое преобразование — центральная симметрия. Значит, гомотетия с коэффициентом -1 является центральной симметрией. Из определения гомотетии следует:

1)    Центр гомотетии переходит сам в себя.

2)     Если k 0 (рис. 2.440), то точки X и  лежат на прямой ОХ по одну сторону от центра гомотетии (так, векторы  сонаправлены).

3)    Если k (рис. 2.442), то точки X и  лежат на прямой ОХ по разные стороны от центра гомотетии (так, векторы  противоположно направлены).

Имеет место теорема (смотри следующий слайд).

Теорема 1:  

Если при гомотетии с коэффициентом k точки X и У переходят в точки X1 и Y1, то X1Y1=kXY.

Из этой теоремы можно получить три следствия — свойства гомотетии:

Следствие 1.   При гомотетии с коэффициентом k расстояние между точками умножается на |k|.

Следствие 2.   При гомотетии всякая прямая переходит в параллельную ей прямую.

Следствие 3.   Гомотетия всякую плоскость переводит в параллельную ей плоскость.

Теорема 2:  

Гомотетичные треугольники всегда подобны.

Понятие преобразования подобия

Гомотетия фигур является частным случаем другого соответствия между фигурами: соответствия подобия или, как его еще называют,  преобразования подобия .

Рассмотрим определение и некоторые свойства преобразований подобия.

Определение:   Преобразование фигуры F называют преобразованием подобия, если при этом преобразовании расстояния между соответствующими точками изменяются в одно и то же число раз, т. е. для любых двух точек X и У фигуры F и точек X', У фигуры F', в которые они переходят, X'Y' = k * XY.

Преобразование подобия переводит прямые в прямые, полупрямые в полупрямые, отрезки в отрезки и сохраняет углы между полупрямыми. Преобразование подобия переводит плоскости в плоскости.

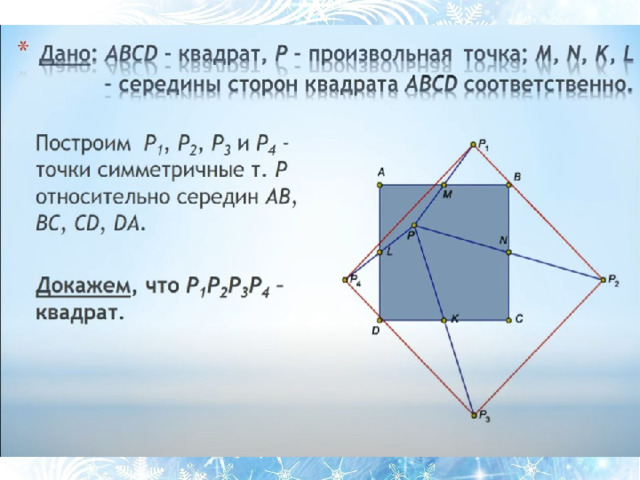
Фигуры называют подобными, если они переводятся одна в другую

  преобразованием подобия.

Это значит, что если произвольные точки X, Y фигуры F при преобразовании подобия переходят в точки X', У' фигуры F', то X'Y' = k * XY, причем число k — одно и то же для всех точек X, Y. Число k является коэффициентом подобия.

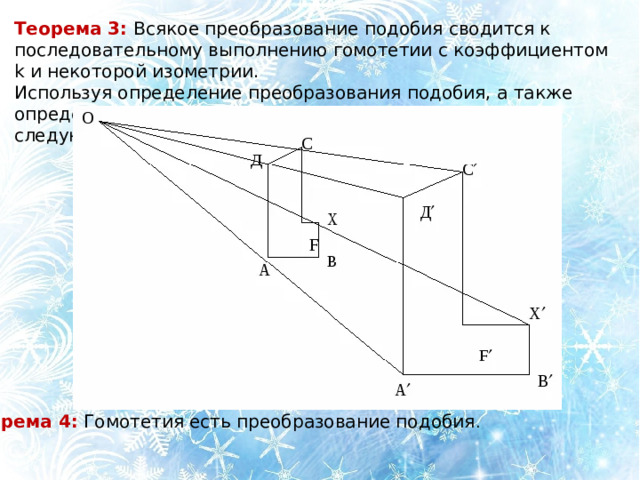
Теорема 3: Всякое преобразование подобия сводится к последовательному выполнению гомотетии с коэффициентом k и некоторой изометрии.

Используя определение преобразования подобия, а также определение и свойства гомотетии, можно доказать следующую теорему.

Теорема 4:  Гомотетия есть преобразование подобия .

ГУ ЛНР «ЛОУ СОШ №41»

Виденеева Н.Н.