Преобразование графиков функций

Муниципальное общеобразовательное учреждение « Лицей №5 имени Ю.А. Гагарина Центрального района Волгограда»

Автор:

Таболаева Марина Васильевна –

учитель математики

МОУ лицея №5

им.Ю.А.Гагарина Волгограда

«Преобразование графиков функций»

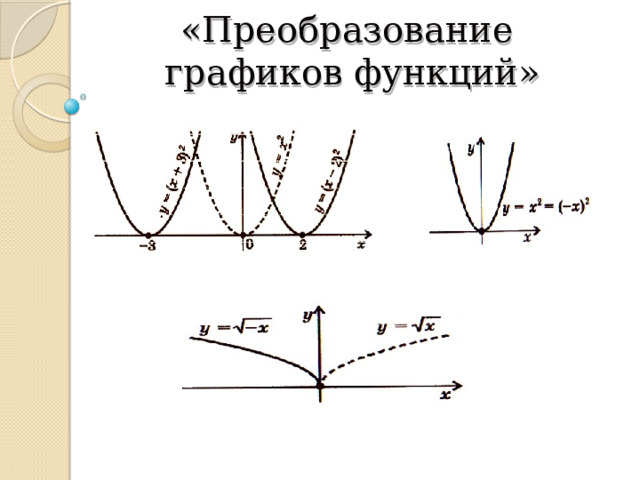
«Преобразование графиков функций»

.

Цели:

• Систематизировать приёмы построения графиков.

• Дать понятие преобразования графиков функций

• Показать применение :

а) при построении графиков функций y = f(x-m), y=f(x)+n, y = ƒ(│x│), y = R ƒ(x ), y = −ƒ(x), y = ƒ(−x).

б)при решение заданий ОГЭ и ЕГЭ.

Функция, область определения и область значений функции.

• Функция – это соответствие между множествами X и Y, при котором каждому элементу множества Х соответствует единственный элемент множества Y.

• Область определения функции – это множество значений аргумента или независимой переменной

• Область значений функции – это все значения, которые принимает функция.

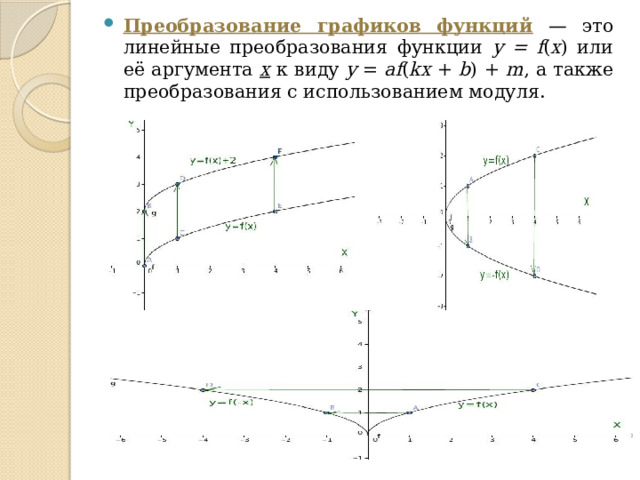
• Преобразование графиков функций — это линейные преобразования функции y = f ( x ) или её аргумента x к виду y = af ( kx + b ) + m , а также преобразования с использованием модуля.

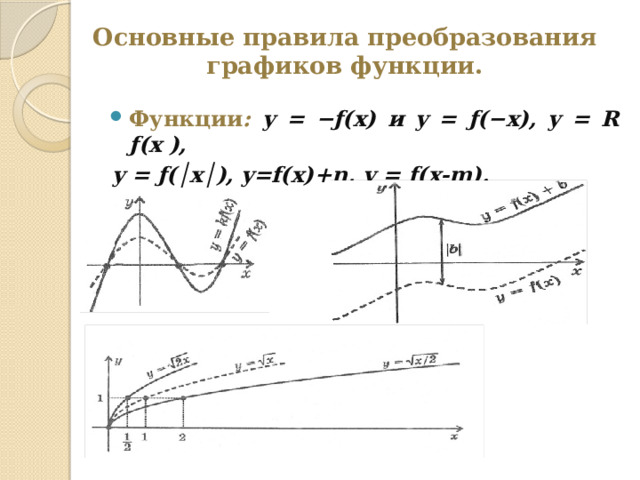
Основные правила преобразования графиков функции.

• Функции : y = −ƒ(x) и y = ƒ(−x), y = R ƒ(x ),

y = ƒ(│x│), y=f(x)+n, y = f(x-m).

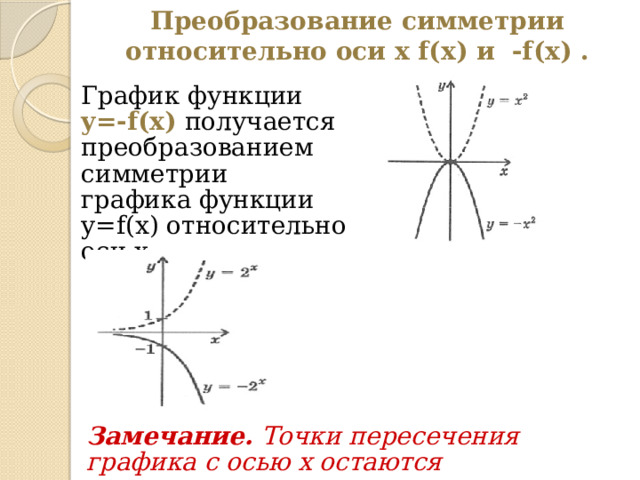
Преобразование симметрии относительно оси x f(x) и -f(x) .

График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.

Замечание. Точки пересечения графика с осью x остаются неизменными.

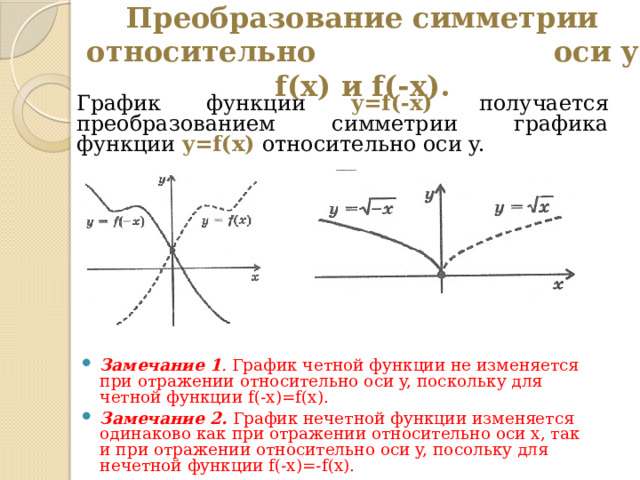
Преобразование симметрии относительно оси y f(x) и f(-x).

График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.

• Замечание 1 . График четной функции не изменяется при отражении относительно оси y, поскольку для четной функции f(-x)=f(x).
• Замечание 2. График нечетной функции изменяется одинаково как при отражении относительно оси x, так и при отражении относительно оси y, посольку для нечетной функции f(-x)=-f(x).

0, то растягиваем полученный график в K раз вдоль оси OY. А если 0Замечание. Точки пересечения графика с осью x остаются неизменными. " width="640"

Преобразование графиков функций y = R ƒ(x ).

• Сначала строим график функции ƒ(x), а затем, если K0, то растягиваем полученный график в K раз вдоль оси OY. А если 0

Замечание. Точки пересечения графика с осью x остаются неизменными.

0 и влево при aЗамечание. График периодической функции с периодом T не изменяется при параллельных переносах вдоль оси x на nT, nZ. " width="640"

Параллельный перенос вдоль оси х f(x) и f(x-а)

• Функция y=f(x-a) . График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a0 и влево при a

Замечание. График периодической функции с периодом T не изменяется при параллельных переносах вдоль оси x на nT, nZ.

Преобразование графиков функции y= │ƒ(x)│.

Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).

Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).

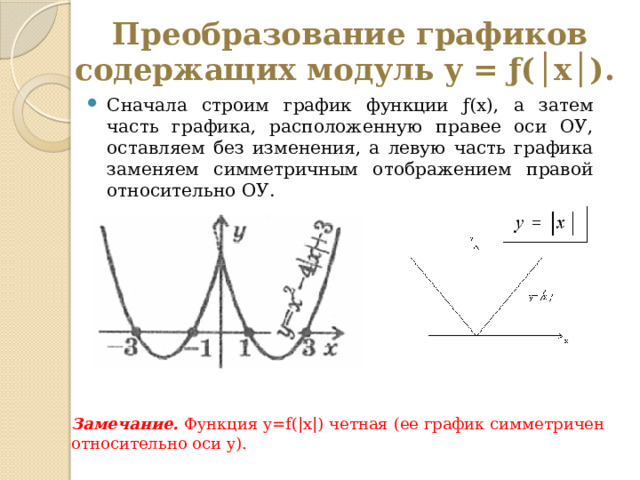
Преобразование графиков содержащих модуль y = ƒ(│x│).

• Сначала строим график функции ƒ(x), а затем часть графика, расположенную правее оси ОУ, оставляем без изменения, а левую часть графика заменяем симметричным отображением правой относительно ОУ.

Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).

0 и вниз при n" width="640"

Параллельный перенос вдоль оси y f(x) и f(x)+n

• График функции y=f(x)+n получается параллельным переносом графика функции y=f(x) вдоль оси y на |n| вверх при n0 и вниз при n

0 и влево при mЗамечание. График периодической функции с периодом T не изменяется при параллельных переносах вдоль оси x на nT, nZ. " width="640"

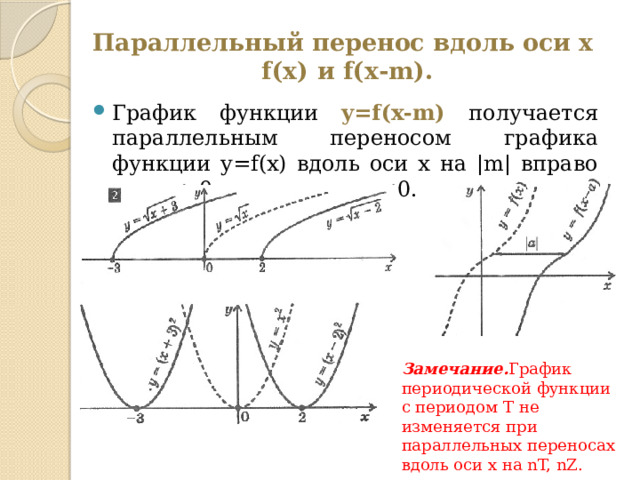
Параллельный перенос вдоль оси x f(x) и f(x-m).

• График функции y=f(x-m) получается параллельным переносом графика функции y=f(x) вдоль оси x на |m| вправо при m0 и влево при m

Замечание. График периодической функции с периодом T не изменяется при параллельных переносах вдоль оси x на nT, nZ.

Применение графиков функций

С помощью графиков функции можно ответить на целый ряд вопросов:

• по заданному значению одной из переменных х или у определить значение другой;
• определять промежутки возрастания и убывания функции;
• определять промежутки знакопостоянства;
• называть значение аргумента, при котором функция принимает наибольшее (наименьшее) значение, а также определять это значение.
• решать уравнения и неравенства

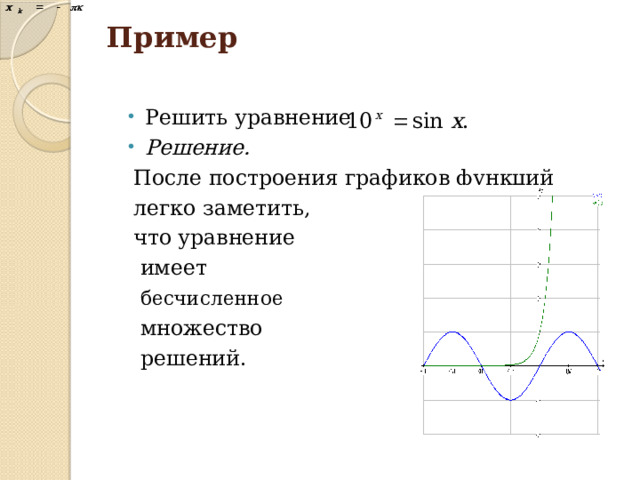
Пример

• Решить уравнение
• Решение.

После построения графиков функций

легко заметить,

что уравнение

имеет

бесчисленное

множество

решений.

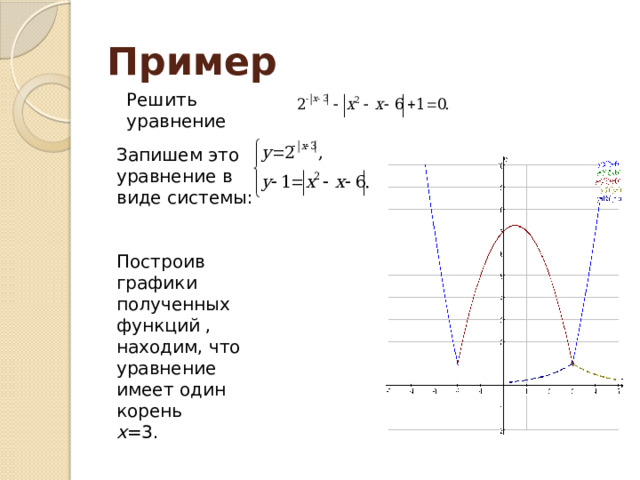
Пример

Решить уравнение

Запишем это уравнение в виде системы:

Построив графики полученных функций ,

находим, что уравнение имеет один корень

x =3.

Выводы:

Перевод алгебраической задачи на язык графиков позволяет избежать громоздких решений. Овладение рациональными методами построения графиков функций и уравнений  способствует успешно выполнять задания ГИА , конкурсные математические задания, содержащие модуль и параметр.

СПАСИБО ЗА ВНИМАНИЕ