Пособие "Начертательная геометрия для школьников"

N

A^l

A

Оглавление

Введение 3

Символика и обозначение 5

Центральное 7

Параллельное 8

Необратимость 9

Способы обратимости 10

Метод числовых отметок 10

Метод Монжа 11

Эпюра Монжа 13

Основные плоскости проекции 13

Переход от пространственной модели

к эпюре Монжа (I октанта) 14

Точка 16

Переход к эпюре Монжа 16

Точки частного положения и их координаты 17

Построение комплексного чертежа

точки нечастного положения с заданными координатами 18

Прямая 19

Переход к эпюре Монжа 19

Прямые частного положении, их свойства и признаки 19

Свойства и признаки: 20

Плоскость 21

Как можно задать часть плоскость 21

Переход к эпюре Монжа 22

Плоскости частного положении, их свойства и признаки 22

Свойства и признаки: 23

Заключение 23

Введение

Начертательная геометрия является одним из разделов геометрии. Здесь пространственные фигуры – совокупность точек, линий, плоскостей (поверхностей). Они изучаются по их проекционным изображениям на плоскости. Основными задачами начертательной геометрии являются:

1. создание метода изображения геометрических фигур на плоскости

2. разработка способов решения позиционных, метрических и конструктивных задач, связанных с этими фигурами, при помощи их изображений на плоскости.

Начертательная геометрия по своему содержанию занимает особое положение среди других наук: она является лучшим средством развития у

человека пространственного воображения, без которого немыслимо никакое инженерное творчество.

Начертательная геометрия - теоретическая база для составления чертежа. Чертеж – это своеобразный язык, с помощью которого, используя всего лишь точки, линии и ограниченное число геометрических знаков, букв и цифр, человек имеет возможность изобразить на поверхности геометрические фигуры или их сочетания (машины, приборы, инженерные сооружения и т.д.). Также этот графический язык является интернациональным и понятен любому технически грамотному человеку независимо от того, на каком языке он говорит.

Проекционные способы начертательной геометрии в авиационной и автомобильной промышленности, архитектуре, строительстве, изобразительном искусстве дают возможность получать наглядные изображения проектируемых объектов.

Естественные науки достигают еще большего расцвета в тех случаях, когда изучаемые свойства сопровождаются доступными для человеческого восприятия наглядными геометрическими моделями.

Способы начертательной геометрии, позволяющие решать математические задачи в их графической интерпретации, находят широкое применение в физике, химии, механике, кристаллографии и многих других науках. Как и другие отрасли математики, начертательная геометрия развивает логическое мышление.

Это далеко не полный перечень вопросов, которые решаются с помощью начертательной геометрии, но даже он не оставляет сомнения, что начертательная геометрия входит в число фундаментальных дисциплин, составляющих основу инженерного образования.

Желаем успехов в изучении данной науки. Надеемся, вам будет интересно…

А теперь вперед, покорять вершины знаний!

Символика и обозначение

А, В, С, D, E …– точки в пространстве

a, b, c, d, e, … – прямые линии в пространстве

Oxyz – система координат в пространстве

Ox, Oy, Oz – оси координат

= – равенство, совпадение

∩ – пересечение (b ∩ Σ = A – прямая b пересекает плоскость Σ в точке А)

// – параллельность (b // d – прямая b параллельна прямой d)

⊥ – перпендикулярность (е ⊥ a – прямая е перпендикулярна прямой а)

∈ – принадлежность элемента множества данному множеству (А ∈ b – точка А принадлежит линии b)

≠, ∉ – знаки, обозначающие отрицание указанных выше отношений

⇒ – знак логического следствия

П1– горизонтальная плоскость проекций

П2– фронтальная плоскость проекций

П3– профильная плоскость проекций

А1, В1, С1, D1, E1 … – проекции точек на П1

А2, В2, С2, D2, E2 … – проекции точек на П2

А3, В3, С3, D3, E3 … – проекции точек на П3

A_X, A_Y, A_Z – точки, являющиеся пересечением линий проекционной связи и соответствующей оси. (А_X⇒OX; A_Y⇒OY; A_Z ⇒OZ).

a – угол а)

Методы проецирования

Познакомимся с терминами…

• С позиции теории множеств любую геометрическую фигуру следует рассматривать как множество всех принадлежащих ей точек. Говоря иначе, всякая геометрическая фигура есть не пустое множество (точек).

• Отображение геометрической фигуры на плоскость можно получить путем проецирования ее точек на эту плоскость.

• Евкли́дово простра́нство –пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность, равную 3. В данном курсе «Начертательной геометрии для школьников» мы будем работать только в евклидовом пространстве.

Разберём основные свойства евклидова пространства ( а конкретно с отношениями принадлежности между элементами евклидова пространства):

1. Если точка А принадлежит прямой а, а прямая а принадлежит плоскости α, то точка А принадлежит плоскости α.

2. Две различные точки А и В всегда принадлежат одной и той же и только одной прямой а или каждой прямой а принадлежат, по крайней мере, две точки А и В.

3. Три различные точки А, В и С, не принадлежащие одной прямой, принадлежат одной и той же и только одной плоскости.

4. Если две точки А и В, принадлежащие прямой а, принадлежат плоскости α, то прямая a принадлежит плоскости α.

5. Две прямые, принадлежащие одной плоскости, могут принадлежать одной точке, но этого может и не быть.

6. Две плоскости могут принадлежать одной и той же прямой, но этого может и не быть.

7. Плоскость и не принадлежащая ей прямая могут принадлежать одной точке, но этого может и не быть.

Примечание! Последние три предложения по существу перефразируют аксиому о параллельности.

Центральное

Человек нередко заимствует строения систем из природы для того, чтобы использовать это в своей деятельности. Например, головной мозг и компьютер состоят из аналогичных частей: зрительная зона коры больших полушарий и видео карта компьютера аналогичны по своим функциям (обеспечивают анализ и отображение изображения); звуковая карта компьютера и слуховая зона коры больших полушарий ответственны за звуковые сигналы и т.д.

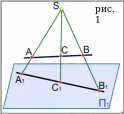
Так и первый появившийся метод проецирования – центральный, подобен системе зрения человеческого глаза. Давайте разберём его на примере рис.1.

Для начала нам нужна плоскость, на которую мы будем проецировать, т.е. плоскость проекции П₁. S – центр проецирования (сравниваемый с человеческим глазом), не лежащий в одной плоскости с П₁ из которого исходят проецирующие лучи. A – точка, которую мы хотим спроецировать на плоскости П₁. Проведём проецирующий луч через точку A. Точка пересечения этого проецирующего луча и плоскости П₁ и есть проекция точки A на плоскость П₁ и обозначается А₁.

На рис.1 кроме точки А на плоскость П₁ спроецированы В и С (через любые 2 точки проходит прямая ⇒ через А и В проходит прямая АВ; С∈АВ). Отсюда следует, что если на прямой АВ есть некоторая точка С в пространстве, то изображение этой точки при центральном проецировании должно попадать на изображение прямой.

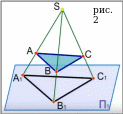
Этим методом проецирования люди пользовались долгое время и заметили, что фигуры сильно искажаются, размеры изменяются, а их взаимоположения в пространстве и на плоскости не совпадают. Например, длины отрезков увеличиваются (это заметно на рис.2, на котором А₁В₁С₁ центральная проекция треугольника АВС), а параллельные прямые пересекаются (этот эффект есть в человеческом зрении).

Параллельное

В связи с искажениями фигур при центральном проецировании ⇒ Гаспар Монж разработал новый способ проецирования – параллельный. Давайте разберём его на примере (рис.3).

Плоскость проекции - П_1. Здесь S^- – направление проецирования, которое не параллельно П₁ – плоскости проекции ⇒ проецирующие лучи – это лучи, параллельные S. Как и в центральном методе здесь A – точка, которую мы хотим спроецировать на плоскости П₁. Точка пересечения проецирующего луча, проходящего через А, и плоскости П₁ – проекция точки A на плоскость П₁ и обозначаетсА₁.

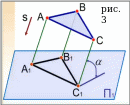На рис.3 А₁В₁С₁ – параллельная проекция треугольника АВС, как видите при рассмотрении с одного и того же ракурса объект в пространстве и его изображение идентичны ⇒ размеры и взаимоположение фигур.

В этом способе разделяют два подвида: косоугольное, при a≠90^о, и ортогональное (прямоугольное), при a=90^о. Вот, именно, ортогональное проецирование даже сейчас считается простым и удобоизмеримым. Оно сохраняет соотношение предметов и их частей и является самым часто используемым.

Необратимость

Научившись проецировать, люди начали пытаться использовать это умение в жизни и передавать друг другу проекции. Например, для изучения предмета, вместо самого объекта. Они заметили, что нельзя с помощью обычных проекционных изображений восстановить предмет и его положение в пространстве единственным правильным способом. Это явление назвали необратимостью проекционного изображения. И оно мешало людям при работе с проекциями, не имеющим спроецированного объекта.

Рассмотрим пример необратимости изображения на рис.4, рис.5:

Нам дана параллельная проекция M₁N₁ геометрической фигуры на плоскости П₁ и направление её проецирования S^- (см. на рис.4) Из данных точек проекций проводим прямые параллельные S^- (как на рис.5), видно, что данная проекция может быть изображением:

• прямой M₁N₁

• прямой M₂N₂

• кривой M₃N₃

  

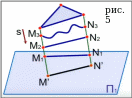
• плоскостью, например, треугольником (как на рис.5)

Способы обратимости

Поняв то, что простые изображения объектов необратимы, учёные стали думать, что можно сделать, чтобы изображения были обратимы. Обратимость проекции – возможность восстановления предмета и его положения в пространстве единственным правильным способом. Всего есть 2 способа обратимости…

Метод числовых отметок

Сущность метода проекций с числовыми отметками заключается в том, что изображаемый объект прямоугольно проецируется только на одну горизонтальную плоскость проекций Π₁. При этом на плоскости отображаются только два его измерения – длина и ширина. Третье измерение – высота изображаемого предмета – выражается числами. Эти числа определяют расстояния от основной плоскости проекций до точек предмета и записываются на чертеже возле символьных обозначений этих точек. (см. рис.6)

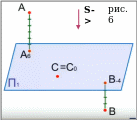
• Число положительно, если проецируемая точка лежит от плоскости проекции с одной и той же стороны, что и направление.

• Отрицательно, если она лежит по другую сторону.

• Равно 0, если точка принадлежит плоскости.

Этот метод используется в строительстве, архитектуре, геодезии…

Метод Монжа

Данный метод, называемый ещё и методом 2-ух плоскостей, изобрёл уже известный нам Гаспар Монж. «Почему объект пространства, имеющий 3 измерения, изображают на одной плоскости, обладающей 2-мя измерениями?» - думал он. Поэтому Монж предложил ортогонально проецировать объект на двух плоскостях сразу, т.е. он добавил ещё одну плоскость П₂ (см. рис.7). П₁ располагалась горизонтально, её назвали горизонтальной. П₂ должна быть перпендикулярна первой и располагаться вертикально, эту плоскость называли фронтальной. Также эти плоскости соприкасаются в прямой, названной осью проекции X.

Метод 2-ух плоскостей работает за счёт того, что на горизонтальной плоскости отображаются такие измерения, как длина и ширина, а на фронтальной – длина и высота. ⇒ Имея две разные ортогональные проекции одного объекта, ты можешь узнать три пространственных измерения точки ⇒ всех остальных фигур.

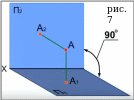
Для начала нужно построить ортогональные проекции точки А на плоскости П₁ и П₂, получим изображения А₁ и А₂. (см. рис.7)

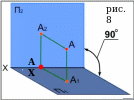
Далее Монж, так как это изображения одной точки, объединил их линиями проекционной связи, которые перпендикулярны к координатной оси X (см. рис.8). Было замечено, что эти отрезки соприкасаются в точке, лежащей на оси Х. Эту точку обозначили как А_Х.

Исходя из этого, Гаспар Монж вывел закон, что для достоверности и обратимости пространственных, 3-х мерных объектов нужно строить минимум 2 изображения. Этим законом воспользовались французские полицейские, которые стали фотографировать преступников и в анфас, и в профиль. Сейчас этим пользуется весь мир, так как есть похожие люди, бывают близнецы, но на одной из фотографий нос с горбинкой, больше оттопырены уши, или заметна родинка, шрам и т.д.

Эпюра Монжа

Основные плоскости проекции

I

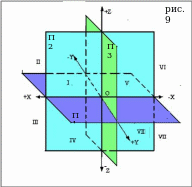
Всего существует 3 основные плоскости проекции (см. рис.9): горизонтальная П₁, фронтальная П₂ и профильная П₃. П₁ и П₂ делят пространство на четверти. П₃ располагается перпендикулярно и к П₁, и к П₂, отражает такие пространственные измерения, как ширина и высота. Профильная плоскость делит каждую четверть, образованную пересечением П₁ и П₂ на 2 части. Из этого следует, что всего пространство делится основными плоскостями проекции на 8 частей-октантов.

В разделе «Метод Монжа» мы рассматривали лишь части плоскостей П₁ и П₂, сами плоскости не умеют ограничений по площади, но мы можем изображать только тот кусочек, который нам нужен.

Четверти и соответствующие им октанты:

1. I и V

2. II и VI

3. III и VII

4. IV и VI

Пересечение 2-х любых плоскостей – прямая, называемая осью.

• Ось X – пересечение П₁ и П₂

• Ось Y – пересечение П₁ и П₃

• Ось Z – пересечение П₂ и П₃

Пересечение всех 3-х плоскостей – точка, обозначаемая О и имеющая координаты (0,0,0)

Положение любой точки в пространстве можно охарактеризовать 3-мя координатами, которые численно обозначают удалённость точки от начала координат О по одной из осей (ОX,ОY,ОZ). Координаты точки А, которая расположена на длине 9-и единичных отрезков, ширине -6 ед.отр. и высоте 4 ед.отр., записываются как А(9;-6;4). Общий вид: А(x,y,z), где x – координата длины, y – ширины, z – высоты.

Единичный отрезок – величина, принимаемая за единицу при геометрических построениях. 

Примечание! В нашем учебном курсе мы будем детально работать только с I октантом, в нём все координаты имеют не отрицательную величину.

Переход от пространственной модели к эпюре Монжа (I октанта)

Эпюру Монжа имеет и другое название – комплексный чертёж. Комплексный чертёж – чертёж, состоящий из 2-х и более ортогональных проекций геометрического образа, он получается при совмещении 3-х плоскостей проекций в 1 (при 2-х проекциях 3-я плоскость не отображается).

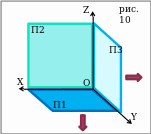
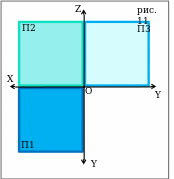
Алгоритм совмещения плоскостей(от рис.10 к рис.11):

• вращать плоскость П₁ вокруг оси ОХ в направлении от себя, пока она не станет той же частью плоскости, что и П₂.

• вращать плоскость П₃ вокруг оси ОZ в направлении от себя, пока она не станет той же частью плоскости, что и П₂.

Точка

Точка – простейший геометрический объект, не имеющий никаких измеримых характеристик. Нульмерный объект.

Переход к эпюре Монжа

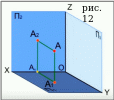
Для начала построим для некоторой точки А, лежащей в I октанте пространства, ортогональные проекции А₁ и А₂, соответственно, на горизонтальную и фронтальную плоскости. Далее соединим эти 2 изображения уже известными нам из раздела «Метод Монжа» линиями связи. (см. рис.12)

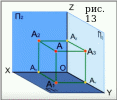
Теперь построим ортогональную проекцию А₃ точки А на профильную плоскость, также соединим это изображение линиями связи с 2-мя другими. (см. рис.13)

Заметим! На рис.13 получился параллелепипед, рёбра которого – это части координатных осей, проецирующих лучей и линий связи. Это объясняется взаимной перпендикулярностью плоскостей между собой, а также взаимной перпендикулярностью линий связи с координатными осями. Из свойства параллелепипедов следует, что его противолежащие рёбра равны.

A_X, A_Y, A_Z – точки, являющиеся пересечением линий проекционной связи между изображениями некоторой точки А на эпюре Монжа и соответствующей оси (OX, OY или OZ).

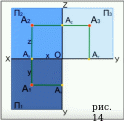
Теперь преобразим данную пространственную модель в комплексный чертёж. Помните, что сам объект и проецирующие лучи на эпюре не отображаются. (см. рис.14)

Заметим! На рис.14: А₁А₂, A₃A_Y, А₂А₃ и A₁A_Y – линии связи. А₁А₂||A₃A_Y и А₂А₃||A₁A_Y.

Для определения точки в пространстве нужно как минимум 2 проекции, т.к.:

• А₁ определяется координатами: x и y

• А₂ определяется координатами: x и z

• А₃ определяется координатами: y и z

Точки частного положения и их координаты

• Лежащие в точке О ⇒A(0;0;0)

• Лежащие на координатных осях:

  • ОХ⇒A(x;0;0),где х≠0⇒x0

  • OY⇒A(0;y;0),где y≠0⇒y0

  • OZ⇒A(0;0;z),где z≠0⇒z0

Заметим! А_Х, А_Y, A_Z – точки, лежащие на координатных осях ⇒ А_Х(х;0;0), А_Y(0;y;0), А_Z(0;0;z), при этом координаты этих точек, отличные от 0, соответствуют координатам проецируемой точки А.

• Лежащие на плоскостях проекций:

  • П₁⇒A(x;y;0),где х,y≠0⇒x,y0

  • П₂⇒A(x;0;z),где х,z≠0⇒x,z0

  • П₃⇒A(0;y;z),где y,z≠0⇒y,z0

Заметим! А₁, А₂, A₃ – точки, лежащие на плоскостях проекций

Построение комплексного чертежа точки нечастного положения с заданными координатами

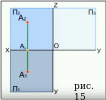Пусть: нам надо построить точку А(40;25;45).(см. рис.15-рис.16)

1. Построим А_Х(40;0;0)

2. Проведём отрезок А_ХА₂=45, где А₂(40;0;45)

3. Проведём отрезок А_ХА₁=25, где А₁(40;25;0)

4. Построим А_Y(0;25;0) и А_Z(0;0;45)

   

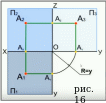
5. Проведём отрезок А₂А_Z=40, где А_Z(0;0;45)

6. Проведём отрезок А_ZА₃=25, где А₃(0;25;45)

7. Проведём отрезки А₁А_Y=40 и А₃А_Y=45

Заметим!

• А_ХА₂+А_ХА₁=А₁А₂=45+25=70,

• А_ZА₂+А_ZА₃=А₂А₃=40+25=65

• У дуги А_YА_Y с центром в точке О радиус равен у=25(рис.16)

• Имея любые 2 проекции точки можно достроить 3-ю

Задание! Построить комплексный чертёж точки А(1;2;3). За единичный отрезок взять 1см.

Прямая

Прямая – геометрический объект, представляющий собой множество точек, имеющий одну измеримую характеристику – длину. Одномерный объект.

Комплексный чертёж

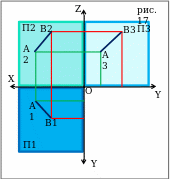Чтобы построить проекцию прямой, нужно построить проекции любых 2-х её точек, а затем провести через них прямую. Луч, отрезок – часть прямой. ⇒ Если нужно построить отрезок или луч, то лучше брать ограничивающие их точки (при луче: одна точка любая, не равная началу; другая ограничивающая – начальная ). Затем соответственно проецируемого объекта соединяем изображения точек.

Комплексный чертёж отрезка общего (нечастного) положения АВ см. на рис.17.

Задание! Построить комплексный чертёж прямой АВ, А(1;2;3) и В(2;3;1). За единичный отрезок взять 1см.

Прямые частного положении, их свойства и признаки

• Проецирующие прямые (перпендикулярные плоскостям проекций)

  • Горизонтально-проецирующие (⊥П₁)

  • Фронтально-проецирующие (⊥П₂)

  • Профильно-проецирующие (⊥П₃)

• Прямые уровня (прямые параллельные плоскостям проекций)

  • Горизонталь(||П₁)

  • Фронталь(||П₂)

  • Профильная прямая(||П₃)

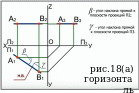
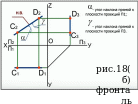
Свойства и признаки:

Если прямая параллельна плоскости проекции, то (рис.18):

• на эту плоскость проецируются в натуральную величину сама прямая и углы наклона её к двум другим плоскостям

• проекции прямой на две другие плоскости проекций параллельны координатным осям.

Если прямая перпендикулярна плоскости проекции, то (рис.19):

• на эту плоскость она проецируются в точку

• проекции прямой на две другие плоскости проекций перпендикулярны координатным осям, а их длины представляют собой натуральную величину

Задание! Постройте комплексный чертёж профильной прямой.

Задание! На рис.19 есть проецирующие прямые и пространственные модели их проекций. Определите, какая из проецируемых прямых является:

а) горизонтально-проецирующей

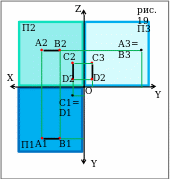
б)фронтально-проецирующей

в)профильно-проецирующей.

Постройте комплексный чертёж того вида прямой, которого нет на рис.19.

Плоскость

Плоскость – геометрический объект, представляющий собой множество точек или прямых и имеющий 2 измеримые характеристики: длину, ширину. Двумерный объект.

Как можно задать часть плоскости

• 3-мя точками, не лежащими на одной прямой

• Отрезком и точкой, не лежащей на этой прямой

• 2-мя пересекающимися отрезками

• параллельными отрезками, которые не принадлежат одной прямой

Переход к эпюре Монжа

Чтобы построить проекции части плоскости, нужно построить проекции точек и (или) отрезков, а затем соответственные изображения соединить отрезками в часть плоскости (см. рис.20).

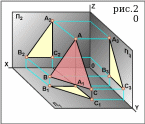
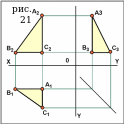
Комплексный чертёж части плоскости АВС , изображеной на рис.20, отображён на рис.21.

Задание! Построить комплексный чертёж плоскости АВС, А(1;2;3), В(2;3;1) и С(3;1;2). За единичный отрезок взять 1см.

Плоскости частного положении, их свойства и признаки

• Плоскости уровня (плоскости параллельные плоскостям проекций)

  • Горизонтальные (|| П₁)

  • Фронтальные (|| П₂)

  • Профильные (|| П₃)

• Проецирующие плоскости (плоскости перпендикулярные плоскостям проекций)

  • Горизонтально-проецирующие (⊥П₁)

  • Фронтально-проецирующие (⊥ П₂)

  • Профильно-проецирующие (⊥П₃)

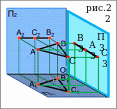
Свойства и признаки:

Если плоскость параллельна плоскости проекции, то (рис.22 –эпюра Монжа горизонтальной плоскости):

• на эту плоскость она проецируются в натуральную величину

• проекции плоскости на две другие плоскости проекций являются прямыми линиями, параллельными координатным осям.

Если плоскость перпендикулярна плоскости проекции, то (рис.23 – эпюра Монжа горизонтально-проецирующей плоскости):

• на эту плоскость проецируются в прямую

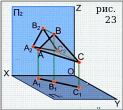
Задание! Постройте комплексные чертежи части фронтальной и профильной, фронтально-проецирующей и профильно-проецирующей плоскостей.

Заключение

Вот и подошёл к концу наш вводный курс начертательной геометрии для школьников. Надеемся, что для вас это было увлекательно и интересно. До новых встреч в следующих наших пособиях об этой увлекательной науке!

О книге

Это издание познакомит вас с основами составления и прочтения проекционных изображений, историей развития данных методов.

Рекомендуется ученикам 8-11 классов, которые собираются поступать на факультеты профессий, требующих инженерное образование.

Автор – Цхай Александра Евгеньевна

г.Хабаровск

2019 год

16