Задание 4. Задачи на вычисление вероятности события
Основой успешного решения этого задания является понимание выпускником термина «вероятность случайного события». Ниже приведена такая расшифровка этого термина, которая интуитивна понятна и удобна в использовании на практике.
Вероятностью того, что в результате проведения некоторого опыта наступит интересующее нас событие, называется отношение числа тех исходов опыта, в которых интересующее нас событие происходит, к числу всех возможных исходов опыта.
1. Новогодняя гирлянда состоит из 250 красных, 300 зелёных, 100 жёлтых и 150 синих лампочек. Одна лампочка перегорела. Какова вероятность, что перегоревшая лампочка красного цвета?
Решение.
Число всех лампочек в гирлянде равно 250 + 300 + 100 + 150 = 800. Так как перегореть могла любая из этих лампочек, то число всех «исходов опыта» равно 800. «Интересующее нас событие» - перегорела красная лампочка. Поскольку красных лампочек 250 и перегореть могла любая из них, то «интересующее нас событие» происходит в 250 исходах опыта. Таким образом, вероятность «интересующего нас события» равна
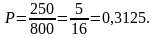
Ответ: 0,3125.
2. На фабрике керамической посуды 8% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 85% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка будет иметь дефект. Ответ округлите до тысячных.
Решение.
Рассмотрим партию из 1000 тарелок. Число тарелок с дефектом в этой партии равно 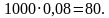 Из этих 80 тарелок при контроле качества будет выявлено
Из этих 80 тарелок при контроле качества будет выявлено 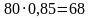 тарелок, а оставшиеся 12 тарелок с дефектом не будут обнаружены и поступят в продажу. Так как из рассматриваемой партии в продажу поступит 1000 – 68 = 932 тарелки, среди которых дефект имеют 12 тарелок, то искомая вероятность равна
тарелок, а оставшиеся 12 тарелок с дефектом не будут обнаружены и поступят в продажу. Так как из рассматриваемой партии в продажу поступит 1000 – 68 = 932 тарелки, среди которых дефект имеют 12 тарелок, то искомая вероятность равна
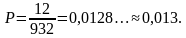
Ответ: 0,013.
3. В одном из регионов производством постельного белья занимаются две фабрики. Первая фабрика выпускает 40% постельного белья, реализуемого в данном регионе, вторая – 60%. Среди комплектов постельного белья, произведённых первой фабрикой, дефекты пошива имеют 5% комплектов, у второй фабрики дефекты пошива имеют 9% комплектов. Найдите вероятность того, что случайно купленный в данном регионе комплект постельного белья имеет дефект.
Решение.
Из каждых 1000 комплектов постельного белья, проданных в данном регионе, первой фабрикой произведены 400 комплектов, а второй – 600 комплектов. Среди 400 комплектов, произведённых первой фабрикой, дефекты пошива имеют 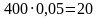 комплектов, а среди 600 комплектов, произведённых второй фабрикой, дефекты пошива имеют
комплектов, а среди 600 комплектов, произведённых второй фабрикой, дефекты пошива имеют 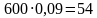 комплекта. Следовательно, из каждых 1000 комплектов постельного белья дефекты будут иметь 20 + 54 = 74 комплекта. Поэтому искомая вероятность равна
комплекта. Следовательно, из каждых 1000 комплектов постельного белья дефекты будут иметь 20 + 54 = 74 комплекта. Поэтому искомая вероятность равна
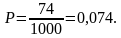
Ответ: 0,074.
4. В конкурсе эстрадной песни «Евровидение» участвуют представители 40 стран, по одному исполнителю от каждой страны. Все выступления разбиваются жеребьёвкой на два полуфинала, по 20 выступлений в каждом. Порядок выступления в полуфинале также определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится во втором полуфинале и будет не ранее, чем 12 по счёту?
Решение.
Если выступление представителя России состоится во втором полуфинале и будет не ранее, чем 12 по счёту, то это означает, что оно будет не менее, чем 32 по счёту среди всех 40 выступлений. «Интересующее нас событие» происходит в 9 случаях из 40 (количество целых чисел от 32 до 40 включая равно 9). Поэтому искомая вероятность равна
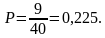
Ответ: 0,225.
5. В командном соревновании по художественной гимнастике участвуют команды 36 стран, в число которых входят Белоруссия, Казахстан, Китай и Россия. Порядок выступления команд определяется жеребьёвкой. Какова вероятность, что команда Китая начнёт выступление позже, чем команда России, но раньше, чем команды Белоруссии и Казахстана? Ответ округлите до тысячных.
Решение.
«Интересующее нас событие» – команда Китая начнёт выступление позже команды России, но раньше, чем команды Белоруссии и Казахстана. Каждой из 36 команд присвоим порядковый номер, в соответствии с тем какой по счёту она начинает выступление (т.е. тот номер, который выпадает ей при жеребьёвке). Командам Белоруссии, Казахстана, Китая и России будут присвоены какие-то 4 из этих номеров, например, 5, 6, 8, 10. Так как вероятность выпадения какой-то конкретной четвёрки номеров одинакова для каждой из возможных четвёрок, то достаточно посчитать вероятность «интересующего нас события» для одной из этих четвёрок. В приведённом выше примере «интересующее нас событие» наступает в следующих двух случаях: команда России начинает выступление пятой, команда Китая – шестой, а команды Белоруссии и Казахстана соответственно восьмой и десятой, или же наоборот – десятой и восьмой. Количество всех способов присвоить командам Белоруссии, Казахстана, Китая и России номера 5, 6, 8, 10 равно 4! =  Поэтому искомая вероятность равна
Поэтому искомая вероятность равна
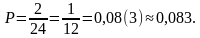
Ответ: 0,083.
Примечание. «Интересующее нас событие» происходит в 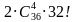 случаях, а общее число всех случаев равно
случаях, а общее число всех случаев равно 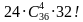 (множитель
(множитель 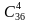 – количество способов выбрать четвёрку номеров для присвоения командам Белоруссии, Казахстана, Китая и России, а множитель 32! соответствует числу способов присвоить номера остальным 32 командам).
– количество способов выбрать четвёрку номеров для присвоения командам Белоруссии, Казахстана, Китая и России, а множитель 32! соответствует числу способов присвоить номера остальным 32 командам).
6. Оценка за контрольную работу по алгебре в 9 классах школы представлены в таблице. Какова вероятность того, что оценка наугад выбранного учащегося 9 «Б» будет отличаться от средней по школе оценки не более, чем на 0,5 балла? Ответ округлите до сотых.
|
| 9 «А» класс | 9 «Б» класс |
| Отметка | «2» | «3» | «4» | «5» | «2» | «3» | «4» | «5» |
| Число учащихся | 2 | 14 | 9 | 3 | 1 | 12 | 10 | 3 |
Решение.
Сначала найдём среднее по школе значение оценки за контрольную. Согласно таблице, оценки по всей школе таковы: «двоек» - 3 шт., «троек» - 26 шт., «четвёрок» - 19 шт., «пятёрок» - 6 шт. Значит, количество учеников, писавших контрольную, равно
3 + 26 + 19 + 6 = 54, сумма баллов всех учеников равна 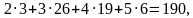 а среднее по школе значение оценки равно
а среднее по школе значение оценки равно 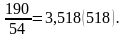
Оценка наугад выбранного учащегося 9 «Б» класса будет отличаться от среднего по школе значения оценки, равного 3,518(518), не более, чем на 0,5 только в том случае, если эта оценка будет «четвёркой».
Поскольку количество «четвёрок» в 9 «Б» равно 10, а общее число учеников из 9 «Б», писавших контрольную, равно 26, то искомая вероятность равна
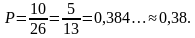
Ответ: 0,38.
7. Пункт контроля качества бракует партию деталей в том случае, если вероятность того, что выбранная наугад деталь окажется бракованной, превышает 0,045. Какое наибольшее число бракованных деталей могло быть в партии из 1100 деталей, если она успешно прошла контроль?
Решение.
Пусть n – искомое число бракованных деталей. Тогда вероятность того, что выбранная наугад деталь окажется бракованной, равна 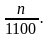 По условию эта вероятность должна не превышать 0,045 (иначе партия была бы забракована), поэтому
По условию эта вероятность должна не превышать 0,045 (иначе партия была бы забракована), поэтому
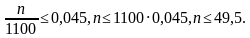
Так как наибольшим целым числом, не превышающим 49,5, является число 49, то 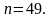
Ответ: 49.
8. В коробке лежат 10 белых и 30 чёрных шаров. Какое наибольшее число чёрных шаров можно вынуть из этой коробки, чтобы после этого вероятность наугад достать из коробки белый шар была не больше 0,6?
Решение.
Пусть из коробки вынуто х чёрных шаров. Тогда в коробке осталось 30 – х чёрных и 10 белых шаров, т.е. всего 40 – х шаров. При этом вероятность наугад достать из коробки белый шар будет равна числу 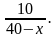 Это число не больше 0,6 в том случае, если
Это число не больше 0,6 в том случае, если
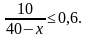
Так как число 40 – х положительно, то предыдущее неравенство равносильно неравенствам: 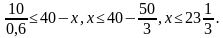 Поэтому наибольшим целым значением х, для которого условие задачи выполнено, является х = 23.
Поэтому наибольшим целым значением х, для которого условие задачи выполнено, является х = 23.
Ответ: 23.
9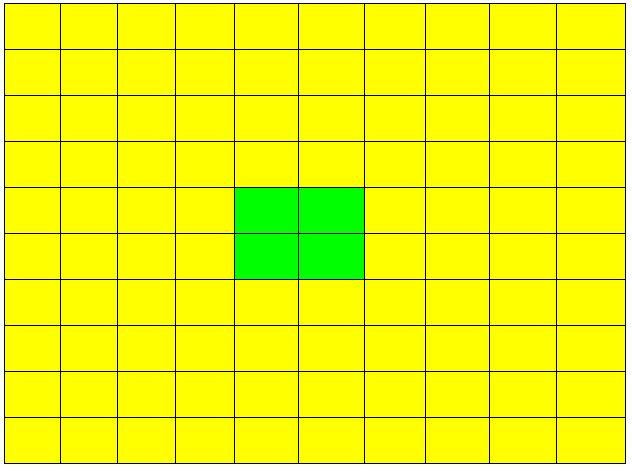 . Квадратный лист бумаги со стороной 10 см разбивают на 100 квадратиков со стороной 1 см и среди этих квадратиков случайным образом выбирают один. Какова вероятность, что расстояние от одной из сторон выбранного квадратика до границы листа составит не более 3 см?
. Квадратный лист бумаги со стороной 10 см разбивают на 100 квадратиков со стороной 1 см и среди этих квадратиков случайным образом выбирают один. Какова вероятность, что расстояние от одной из сторон выбранного квадратика до границы листа составит не более 3 см?
Решение.
Расстояние от одной из сторон выбранного квадратика до границы листа составляет не более 3 см в том случае, если этот квадратик лежит внутри «каёмки» шириной 4 клеточки, примыкающей к сторонам квадрата: на рисунке выделена жёлтым цветом. Те из квадратиков, которые лежат вне этой «каёмки», образуют квадрат со стороной 2, дополняющий «каёмку» до квадрата 10 х 10, число этих квадратиков равно 4. Поэтому число квадратиков внутри «каёмки» равно 100 – 4 = 96. Отсюда получаем, что искомая вероятность равна
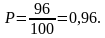
Ответ: 0,96.
10. На гранях игрального кубика отмечены числа от 1 до 6. Найдите вероятность того, что при бросании двух игральных кубиков сумма выпавших на них очков составит не больше 9. Ответ округлите до тысячных.
Решение.
При бросании двух игральных кубиков число всех возможных исходов опыта равно числу различных комбинаций верхних граней этих кубиков (т.к. именно верхняя грань кубика указывает число выпавших очков), т.е. равно 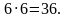 Вместо нахождения числа «интересующих нас» исходов опыта, найдём сначала число всех остальных исходов опыта – тех, в которых сумма выпавших очков больше 9.
Вместо нахождения числа «интересующих нас» исходов опыта, найдём сначала число всех остальных исходов опыта – тех, в которых сумма выпавших очков больше 9.
Пусть (n; m) – пара чисел, соответствующая комбинации верхних граней кубиков. Простым перебором находим, что неравенство  выполняется для шести из этих пар чисел, а именно, для пар (4; 6), (6; 4), (5; 5), (5; 6), (6; 5), (6; 6). Таким образом, число тех исходов опыта, в которых выпадает более 9 очков, равно 6. Поэтому вероятность выпадения более 9 очков равна
выполняется для шести из этих пар чисел, а именно, для пар (4; 6), (6; 4), (5; 5), (5; 6), (6; 5), (6; 6). Таким образом, число тех исходов опыта, в которых выпадает более 9 очков, равно 6. Поэтому вероятность выпадения более 9 очков равна  а вероятность выпадения не более 9 очков равна
а вероятность выпадения не более 9 очков равна
Ответ: 0,833.
Примечание. Вместо нахождения вероятности интересующего нас события можно найти вероятность противоположного события. Если вероятность противоположного события равна р, то искомая вероятность будет равна 1 – р. Указанный приём является очень эффективным для тех задач, где число случаев, в которых наступает противоположное событие, значительно меньше числа тех случаем, в которых происходит интересующее нас событие.
11. Коля дважды бросает игральный кубик. В сумме у него выпало 6 очков. Найдите вероятность того, что при первом броске выпало не больше 3 очков.
Решение.
Пусть n – число, выпавшее при первом броске игрального кубика Колей, а m – число, выпавшее при втором броске. Перебором находим, что равенство n + m = 6 выполняется для следующих пар чисел (n; m): (1; 5), (5; 1), (2; 4), (4; 2), (3; 3). Таким образом, число всех исходов опыта, возможных по условию задачи, равно 5. Так как нас интересуют те исходы опыта, в которых  а это выполнено в трёх из пяти вышеперечисленных случаев – для пар (1; 5), (2; 4), (3; 3), то искомая вероятность равна
а это выполнено в трёх из пяти вышеперечисленных случаев – для пар (1; 5), (2; 4), (3; 3), то искомая вероятность равна

Ответ: 0,6.
12. Монету подбрасывают несколько раз так, что каждый раз с равной вероятностью выпадает «орёл» или «решка». Найдите вероятность того, что при первых трёх подбрасываниях выпадет одна и та же сторона монеты (т.е. либо все три раза «орёл», либо все три раза «решка»).
Решение.
При трёх подбрасываниях монеты имеется 23 = 8 различных вариантов последовательности выпадений «о» или «р». Одна и та же сторона монеты выпадает три раза подряд в двух из этих вариантов: либо «о», «о», «о»; либо «р», «р», «р». Поэтому искомая вероятность равна

Ответ: 0,25.
13. Монету подбрасывают несколько раз так, что каждый раз с равной вероятностью выпадает «орёл» или «решка». Найдите вероятность того, что при четырёх подбрасываниях монеты и «орёл» и «решка» выпадут хотя бы по одному разу.
Решение.
Так как при четырёх подбрасываниях монеты имеется 24 = 16 различных вариантов последовательности выпадений «о» или «р», а вариантов, в которых все четыре раза выпадает одна и та же сторона монеты, всего два (либо все четыре раза «о», либо все четыре раза «р»), то число различных вариантов, в которых и «орёл» и «решка» выпадают хотя бы по одному разу, равно 16 – 2 = 14. Поэтому искомая вероятность равна
Ответ: 0,875.
14. Перед началом волейбольного матча жребием определяется команда, которая будет первой осуществлять подачу. Команда «Рубин» по очереди играет с командами «Сапфир», «Изумруд», «Аметист» и «Топаз». Найдите вероятность того, команда «Рубин» будет первой осуществлять подачу не более, чем в двух играх.
Решение.
Будем считать, что перед началом игры подбрасывают монету, и команда «Рубин» первой осуществляет подачу, если выпал «орёл», а если выпала «решка», то первыми подают соперники. Тогда вопрос задачи можно переформулировать так: какова вероятность, что при четырёх подбрасываниях монеты «орёл» выпадет не более двух раз?
При четырёх подбрасываниях монеты имеется 24 = 16 различных вариантов последовательности выпадений «о» или «р». Вместо нахождения числа интересующих нас вариантов (в которых «орёл» выпал не более двух раз), найдём число вариантов противоположного события – «орёл» выпал не менее трёх раз.
Пусть «орёл» выпал не менее трёх раз, тогда он выпал либо ровно три раза, либо все четыре раза. Если в последовательности выпадений «о» встречается ровно три раза, то «р» встречается ровно один раз – это выполняется для четырёх вариантов: «р» находится или на 1-ом месте, или на 2-ом, или на 3-ем, или на 4-ом. Число вариантов последовательности выпадений, в которых «о» находится на всех четырёх позициях, равно 1. Таким образом, число вариантов последовательности выпадений, в которых «о» встречается не менее трёх раз, равно 4 + 1 = 5. Отсюда получаем, что число вариантов, в которых «о» встречается не более двух раз, равно 16 – 5 = 11, а искомая вероятность равна
Ответ: 0,6875.
15. Для некоторого стрелка вероятность попадания в мишень равна 0,7. Найдите вероятность того, что сделав четыре выстрела, стрелок попадёт в мишень не более двух раз.
Решение.
Если вероятность попадания в мишень равна 07, то вероятность промаха равна
1 – 0,7 = 0,3. В записи результатов выстрелов попадание будем обозначать знаком «+», а промах знаком «–».
Вместо вероятности «интересующего нас» события найдём вероятность противоположного события – стрелок попал в мишень более двух раз, т.е либо три раза, либо все четыре раза. Для этого противоположного события в записи результатов стрельбы будет последовательность из 4-х знаков «+» или «–», в которой количество знаков «+» равно либо 3, либо 4.
Событие 3 знака «+» и 1 знак «–» разбивается на следующие четыре исхода:
{–, +, +, +}; {+, –, +, +}; {+, +, –, +}; {+, +, +, –}. Так как вероятность появления в результатах стрельбы каждого из значений «+» равна 0,7, а вероятность появления знака «–» равна 0,3, то вероятности каждого из приведённых выше четырёх результатов стрельбы равны  Поэтому вероятность того, что при четырёх выстрелах будет три попадания и один промах, равна
Поэтому вероятность того, что при четырёх выстрелах будет три попадания и один промах, равна 
Вероятность четырёх попаданий равна 0,74. Следовательно, вероятность «противоположного» события равна
0,74 + а вероятность «интересующего нас» события равна
Р = 1 – 0,6517 = 0, 3483.
Ответ: 0,3483.
16. В коробке лежат два чёрных, два белых и один красный шар. Из коробки наугад вынимают два шара. Какова вероятность, что вынутые шары окажутся одного цвета?
Решение. Способ 1
Так как в коробке лишь 1 красный шар, то вынутые шары могут оказаться одноцветными лишь в том случае, если они оба белые или оба чёрные. Будем считать, что шары извлекают из коробки по очереди – сначала один, а затем другой, и найдём вероятность того, что оба вынутых шара окажутся белыми.
Первый вынутый шар оказывается белым в двух случаях из пяти (всего шаров пять, из них белых – два). Если первый шар оказался белым, то второй вынутый шар окажется белым лишь в одном случае из четырёх возможных (среди оставшихся 4 шаров белым является лишь один). Поэтому и первый, и второй шар окажутся белыми в числе случаев, равном  от числа всех возможных случаев. То есть вероятность того, что оба вынутых шара окажутся белыми, равна 0,1.
от числа всех возможных случаев. То есть вероятность того, что оба вынутых шара окажутся белыми, равна 0,1.
Вероятность того, что оба вынутых шара окажутся чёрными, также равна 0,1 (приведённое выше рассуждение можно повторить дословно, заменив белый цвет на чёрный). Следовательно, вероятность того, что оба вынутых шара окажутся одного цвета, равна 0,1 + 0,1 = 0,2.
Способ 2
Так как всего в ящике пять шаров, то число всех способов выбрать какие-то два из этих шаров равно Среди всех способов выбрать два шара из пяти имеющихся ровно для двух способов выбора эти шары будут одноцветными – либо оба выбранных шара белые, либо оба чёрные. Таким образом, вероятность того, что будут выбраны шары одного цвета, равна

Ответ: 0,2.
17. Таня написала в блокноте трёхзначное число, делящееся на 28. Ваня должен угадать это число, написав шесть трёхзначных чисел, делящихся на 28, а затем сравнив эти числа с числом, написанным Таней. Какова вероятность, что Ваня угадает загаданное Таней число?
Решение.
Наименьшим трёхзначным числом, делящимся на 28, является число  , а наибольшим трёхзначным числом, делящимся на 28, является число
, а наибольшим трёхзначным числом, делящимся на 28, является число  Поэтому количество трёхзначных чисел, делящихся на 28, равно 35 – 3 = 32 (таких чисел ровно столько же, сколько натуральных чисел от 4 до 35 включая). Так как Ваня пишет какие-то шесть из этих чисел, то вероятность того, что он угадает загаданное Таней число, равна
Поэтому количество трёхзначных чисел, делящихся на 28, равно 35 – 3 = 32 (таких чисел ровно столько же, сколько натуральных чисел от 4 до 35 включая). Так как Ваня пишет какие-то шесть из этих чисел, то вероятность того, что он угадает загаданное Таней число, равна
Ответ: 0,1875.
18. Из трёхзначных чисел наугад выбирают одно число. Какова вероятность, что будет выбрано число, меньшее 700 и делящееся на 3, но не делящееся на 7?
Решение.
Число всех возможных исходов опыта равно количеству трёхзначных чисел, т.е. равно 900 (могло быть выбрано любое число от 100 до 999). Найдём число «интересующих нас» исходов опыта. Поскольку наименьшим трёхзначным числом, делящимся на 3, является число  , а наибольшим число
, а наибольшим число  то количество трёхзначных чисел, меньших 700 и делящихся на 3, равно 233 – 33 = 200 – это числа
то количество трёхзначных чисел, меньших 700 и делящихся на 3, равно 233 – 33 = 200 – это числа  Заметим, что 35 =
Заметим, что 35 =  а 231 =
а 231 =  поэтому среди указанных выше чисел делящимися на 7 являются числа ( количество которых равно 33 – 4 =29. Таким образом, количество трёхзначных чисел, меньших 700 и делящихся на 3, но не делящихся на 7, равно 200 – 29 = 171, а искомая вероятность равна
поэтому среди указанных выше чисел делящимися на 7 являются числа ( количество которых равно 33 – 4 =29. Таким образом, количество трёхзначных чисел, меньших 700 и делящихся на 3, но не делящихся на 7, равно 200 – 29 = 171, а искомая вероятность равна
Ответ: 0,19.
19. Из трёхзначных чисел наугад выбирают одно число. Какова вероятность, что будет выбрано число, десятичная запись которого содержит хотя бы одну цифру 6?
Решение.
Вместо нахождения вероятности интересующего нас события найдём сначала вероятность противоположного события – то есть вероятность того, что будет выбрано число, десятичная запись которого не содержит ни одной цифры 6.
Найдём количество трёхзначных чисел, десятичная запись которых не содержит ни одной цифры 6. Для первой цифры такого числа имеется 8 возможностей – все цифры от 1 до 9 за исключением цифры 6, а для второй и третьей цифры такого числа имеется по 9 возможностей – все цифры от 0 до 9 за исключением цифры 6. Следовательно, количество таких чисел равно  а вероятность выбрать такое число среди всех трёхзначных чисел равна
а вероятность выбрать такое число среди всех трёхзначных чисел равна
Так как вероятность противоположного события равна 0,72, то искомая вероятность равна
Р = 1 – 0,72 = 0,28.
Ответ: 0,28.
20. Из шестизначных чисел наугад выбирают одно число. Какова вероятность, что будет выбрано число, десятичная запись которого содержит ровно три цифры 7?
Решение.
Найдём сначала количество таких шестизначных чисел, содержащих в десятичной записи три цифры 7, в которых первая цифра отлична от 7. Для выбора первой цифры такого числа имеется 8 возможностей – все цифры от 1 до 9 за исключением 7. Для выбора остальных пяти цифр такого числа имеется  способов:
способов:  число способов определить те три позиции, на которых будут находиться цифры 7,
число способов определить те три позиции, на которых будут находиться цифры 7,  число способов выбрать де оставшихся цифры (для каждой из этих цифр имеется 9 возможностей – все цифры от 0 до 9 за исключением 7). Следовательно, количество шестизначных чисел, содержащих в десятичной записи три цифры 7, в которых первая цифра отлична от 7, равно
число способов выбрать де оставшихся цифры (для каждой из этих цифр имеется 9 возможностей – все цифры от 0 до 9 за исключением 7). Следовательно, количество шестизначных чисел, содержащих в десятичной записи три цифры 7, в которых первая цифра отлична от 7, равно
Теперь найдём количество таких шестизначных чисел, содержащих в десятичной записи три цифры 7, в которых первой цифрой является 7. Для выбор пяти цифр такого числа (со 2-ой по 6-ую цифры) имеется  способов:
способов:  число способов определить те две позиции, на которых будут находиться цифры 7,
число способов определить те две позиции, на которых будут находиться цифры 7,  число способов выбрать три оставшихся цифры.
число способов выбрать три оставшихся цифры.
Из результатов двух предыдущих абзацев следует, что количество всех шестизначных чисел, содержащих в десятичной записи три цифры 7, равно
6480 + 7290 = 13770. Осталось заметить, что поскольку количество всех шестизначных чисел равно 900000, то искомая вероятность равна
Ответ: 0,0153.
21. У Дины в копилке лежит 15 рублёвых, 12 двухрублёвых и 9 пятирублёвых монет. Дина наугад достаёт из копилки две монеты. Найдите вероятность того, что она достанет не более шести рублей. Ответ округлите до тысячных.
Решение.
Вместо нахождения вероятности интересующего нас события найдём сначала вероятность противоположного события – Дина достала из копилки более 6 рублей или, что то же самое, не меньше 7 рублей.
Если из копилки вынуто не меньше 7 рублей двумя монетами, то одна из этих монет обязательно пятирублёвая, а другая – либо пятирублёвая, либо двухрублёвая.
Достать из копилки две пятирублёвые монета Дина может способами. А одну пятирублёвую и одну двухрублёвую монеты Дина может достать  способами. Так как всего у Дины 36 монет, то выбрать две из них можно
способами. Так как всего у Дины 36 монет, то выбрать две из них можно
способами.
Таким образом, вероятность того, что Дина достанет не меньше 7 рублей, равна, А искомая вероятность равна
Ответ: 0,771.
22. При подготовке к зачётам по двум предметам студент выучил по одному предмету 26 вопросов из 35, а по другому предмету – 21 вопрос из 32. Чтобы получить «зачёт» по предмету, студенту необходимо ответить на один вопрос, случайным образом выбранный из списка вопросов по данному предмету. Какова вероятность, что студент не получит «зачёт» хотя бы по одному из этих двух предметов?
Решение.
Вместо нахождения вероятности интересующего нас события найдём сначала вероятность противоположного события – то есть вероятность того, что студент получит «зачёт» по обоим предметам.
Число вариантов выбора одного вопроса по первому предмету и одного вопроса по второму равно  Студент знает ответ на оба вопроса для
Студент знает ответ на оба вопроса для  из этих вариантов. Поэтому вероятность того, что студент получит «зачёт» по обоим предметам, равна Тогда искомая вероятность равна
из этих вариантов. Поэтому вероятность того, что студент получит «зачёт» по обоим предметам, равна Тогда искомая вероятность равна
Ответ: 0,5125.
23. Некоторый прибор состоит из трёх блоков. Если в работе одного из блоков происходит сбой, прибор отключается. Вероятность сбоя в течение года для первого блока составляет 0,2, для второго блока – 0,3, а для третьего блока – 0,1. Какова вероятность, что в течение года произойдёт хотя бы одно отключение данного прибора?
Решение.
Вместо нахождения вероятности интересующего нас события найдём сначала вероятность противоположного события – то есть вероятность того, что в течение года не произойдёт ни одного отключения данного прибора.
Вероятность работы без единого сбоя в течение года для 1-го блока равна
1 – 0,2 == 0,8, для 2-го блока эта вероятность равна 1 – 0,3 = 0,7, а для 3-го блока эта вероятность равна 1 – 0,1 = 0,9. Отсюда находим, что вероятность работы без единого сбоя в течение года всех трёх блоков (т.е. вероятность того, что в течение года не произойдёт ни одного отключения данного прибора) равна
Так как вероятность противоположного события равна 0,504, то искомая вероятность равна
Ответ: 0,496.
24. При стрельбе по цели артиллерийская система делает несколько выстрелов. Вероятность уничтожения некоторой цели при первом выстреле этой системы равна 0,8, а при каждом последующем выстреле – 0,9. Какое наименьшее число выстрелов должна сделать эта система для того, чтобы вероятность уничтожения цели составляла не менее 0,998?
Решение.
Сначала найдём вероятность того, что при n выстрелах данной артиллерийской системы цель не будет поражена. Из условия следует, что вероятность промаха по цели при первом выстреле системы равна 1 – 0,8 = 0,2, а вероятность промаха по цели при каждом следующем выстреле равна 0,1. Поэтому вероятность промаха по цели при двух выстрелах равна  вероятность промаха по цели при трёх выстрелах равна
вероятность промаха по цели при трёх выстрелах равна
 и продолжая аналогично далее, получаем, что вероятность промаха по цели при n выстрелах равна
и продолжая аналогично далее, получаем, что вероятность промаха по цели при n выстрелах равна 
Вероятность уничтожения цели составляет не менее 0,998  вероятность промаха по цели составляет не более 0,002. Поэтому если n – искомое значение числа выстрелов, то Таким образом, наименьшее число выстрелов, при котором вероятность промаха по цели составит не более 0,002, равно 3.
вероятность промаха по цели составляет не более 0,002. Поэтому если n – искомое значение числа выстрелов, то Таким образом, наименьшее число выстрелов, при котором вероятность промаха по цели составит не более 0,002, равно 3.
Ответ: 3.
25. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом анализ даёт положительный результат с вероятностью 0,99. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,02. Известно, что 10% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Решение.
Рассмотрим выборку анализов 1000 пациентов, поступивших с подозрением на гепатит. Согласно условию, из этих 1000 пациентов число действительно больных гепатитом равно  Среди результатов анализа этих 100 пациентов положительными будут
Среди результатов анализа этих 100 пациентов положительными будут  анализов, а среди результатов анализа остальных 900 пациентов, не больных гепатитом, положительными будут
анализов, а среди результатов анализа остальных 900 пациентов, не больных гепатитом, положительными будут  анализов. Таким образом, общее число положительных результатов будет равно 99 + 18 = 117 случаев на каждую тысячу анализов. Поэтому искомая вероятность равна
анализов. Таким образом, общее число положительных результатов будет равно 99 + 18 = 117 случаев на каждую тысячу анализов. Поэтому искомая вероятность равна

Ответ: 0,117.
26. В некоторой местности летнее утро бывает либо ясным, либо облачным. Наблюдения показали, что летнее утро бывает ясным с вероятностью 0,6, причём если утро ясное, то вероятность дождя в течение дня равна 0,3, а если утро облачное – вероятность дождя в этот день равна 0,95. Какова вероятность того, что в случайно выбранный летний день дождя не будет?
Решение.
Для удобства будем считать, что «летнее» время длится в данной местности ровно 100 дней. Так как летнее утро ясное с вероятностью 0,6, то из 100 дней ясными будут 60, а облачными – 40.
Вероятность дождя в ясный день, равна 0,3, поэтому из 60 ясных дней будет
 дней, в течение которых пройдёт дождь.
дней, в течение которых пройдёт дождь.
Вероятность дождя в облачный день, равна 0,95, поэтому из 40 облачных дней будет  дней, в течение которых пройдёт дождь.
дней, в течение которых пройдёт дождь.
Таким образом, из 100 дней дождь будет в течение 18 + 38 = 56 дней, а не будет дождя в течение 44 дней, т.е. искомая вероятность равна

Ответ: 0,44.
27. В Волшебной стране бывает два типа погода: хорошая и отличная. При этом, установившись утром, погода держится неизменной весь день, а вероятность изменения погоды на следующий день равна 0,3. Найдите вероятность того, что 5 сентября в Волшебной стране будет хорошая погода, если 1 сентября погода в Волшебной стране была отличная.
Решение.
Так как вероятность изменения погоды на следующий день равна 0,3, то вероятность того, что погода не изменится, равна 1 – 0,3 = 0,7.
Для погоды на 2, 3, 4 и 5 сентября есть 8 вариантов: ОООХ, ХООХ, ОХОХ, ООХХ, ХХОХ, ХОХХ, ОХХХ, ХХХХ (здесь Х — хорошая, О — отличная погода). Найдем вероятности наступления такой погоды:
Р(ОООХ) = 
Р(ХООХ) =
Р(ОХОХ) =
Р(ООХХ) =
Р(ХХОХ) =
Р(ХОХХ) =
Р(ОХХХ) =
Р(ХХХХ) = 
Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:
Р(ОООХ) + Р(ХООХ) + Р(ОХОХ) + Р(ООХХ) + P(ХХОХ) + P(ХОХХ) + P(ОХХХ) + P(ХХХХ) = = 0,1029 + 0,0189 +0,0189 + 0,1029 + 0,0189 + 0,0189 + 0,1029 + 0,1029 = 0,4872.
Ответ: 0,4872.
2 8. На рисунке показана схема дорог, ведущих из пункта А в пункт D. Водитель случайным образом выбирает один из возможных маршрутов (при этом маршруты, проходящие повторно через пункт А, он не рассматривает). Какова вероятность, что будет выбран маршрут, не проходящий через пункт В?
Решение.
Из пункта А можно попасть напрямую в пункт В двумя способами (пункт В соединяют с пунктом А две дороги). Из пункта В можно проехать в пункт D пятью различными способами – двумя путями, проходящими через промежуточный пункт С, и тремя дорогами, соединяющими пункт В с пунктом D напрямую. Таким образом, существует  способов попасть из А в D по маршруту, первая дорога которого проходит через пункт В.
способов попасть из А в D по маршруту, первая дорога которого проходит через пункт В.
Так как пункт С соединяют с пунктом А три дороги, а из пункта С в пункт D можно проехать пятью различными способами, то существует  способов попасть из А в D по маршруту, первая дорога которого проходит через пункт С. При этом только
способов попасть из А в D по маршруту, первая дорога которого проходит через пункт С. При этом только
3∙2=6 из этих маршрутов не проходят через пункт В.
Таким образом, всего существует 10 + 15 = 25 различных маршрутов из пункта А в пункт D, из которых только 6 маршрутов не проходят через пункт В. Поэтому искомая вероятность выбрать маршрут, не проходящий через пункт В, равна
О твет: 0,24.
29. На рисунке показана схема дорог из пункта А в пункт D с указанием их длины – рядом с каждой линией указано число, обозначающее длину соответствующей дороги в км. Водитель наугад выбирает маршрут из А в D (при этом маршруты, проходящие повторно через пункт А, он не рассматривает). Какова вероятность, что им будет выбран маршрут наименьшей возможной длины?
Решение.
Общее число различных маршрутов из пункта А в пункт D подсчитывается аналогично тому, как это сделано в решении предыдущей задачи: маршрутов, первая дорога которых проходит через пункт В,  маршрутов, первая дорога которых проходит через пункт С,
маршрутов, первая дорога которых проходит через пункт С,  всего различных маршрутов из пункта А в пункт D –
всего различных маршрутов из пункта А в пункт D –
8 +8 = 16.
Легко видеть, что наименьшая длина маршрута из А в D равна 14 км, а число маршрутов, длина которых равна 14 км, равна трём: два маршрута, проходящие, проходящие по дороге из А в В длиной 6 км и далее напрямую из В в D по дороге длиной 8 км, а также один маршрут, проходящий по дороге из А в С длиной 9 км и далее напрямую из С в D по дороге длиной 5 км.
Следовательно, искомая вероятность выбрать маршрут наименьшей возможной длины равна
Ответ: 0,1875.
30. На отрезке [–5; 15] числовой оси случайным образом отмечают одну точку. Какова вероятность, что координата отмеченной точки будет больше –2, но меньше 11?
Решение.
По определению «геометрической вероятности», вероятность выбрать точку внутри промежутка L так, чтобы она принадлежала некоторому промежутку l, расположенному внутри L, равна отношению длин промежутков l и L.
Согласно данному выше определению, искомая вероятность того, что отмеченная точка окажется внутри промежутка (–2; 11), равна отношению длины промежутка (–2; 11) к длине промежутка [–5; 15], т.е. равна
Ответ: 0,65.







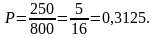
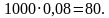 Из этих 80 тарелок при контроле качества будет выявлено
Из этих 80 тарелок при контроле качества будет выявлено 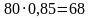 тарелок, а оставшиеся 12 тарелок с дефектом не будут обнаружены и поступят в продажу. Так как из рассматриваемой партии в продажу поступит 1000 – 68 = 932 тарелки, среди которых дефект имеют 12 тарелок, то искомая вероятность равна
тарелок, а оставшиеся 12 тарелок с дефектом не будут обнаружены и поступят в продажу. Так как из рассматриваемой партии в продажу поступит 1000 – 68 = 932 тарелки, среди которых дефект имеют 12 тарелок, то искомая вероятность равна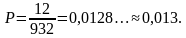
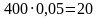 комплектов, а среди 600 комплектов, произведённых второй фабрикой, дефекты пошива имеют
комплектов, а среди 600 комплектов, произведённых второй фабрикой, дефекты пошива имеют 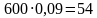 комплекта. Следовательно, из каждых 1000 комплектов постельного белья дефекты будут иметь 20 + 54 = 74 комплекта. Поэтому искомая вероятность равна
комплекта. Следовательно, из каждых 1000 комплектов постельного белья дефекты будут иметь 20 + 54 = 74 комплекта. Поэтому искомая вероятность равна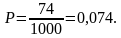
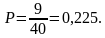
 Поэтому искомая вероятность равна
Поэтому искомая вероятность равна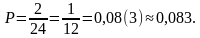
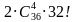 случаях, а общее число всех случаев равно
случаях, а общее число всех случаев равно 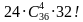 (множитель
(множитель 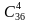 – количество способов выбрать четвёрку номеров для присвоения командам Белоруссии, Казахстана, Китая и России, а множитель 32! соответствует числу способов присвоить номера остальным 32 командам).
– количество способов выбрать четвёрку номеров для присвоения командам Белоруссии, Казахстана, Китая и России, а множитель 32! соответствует числу способов присвоить номера остальным 32 командам).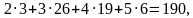 а среднее по школе значение оценки равно
а среднее по школе значение оценки равно 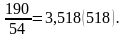
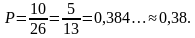
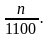 По условию эта вероятность должна не превышать 0,045 (иначе партия была бы забракована), поэтому
По условию эта вероятность должна не превышать 0,045 (иначе партия была бы забракована), поэтому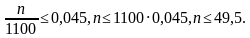
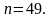
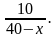 Это число не больше 0,6 в том случае, если
Это число не больше 0,6 в том случае, если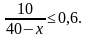
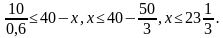 Поэтому наибольшим целым значением х, для которого условие задачи выполнено, является х = 23.
Поэтому наибольшим целым значением х, для которого условие задачи выполнено, является х = 23. . Квадратный лист бумаги со стороной 10 см разбивают на 100 квадратиков со стороной 1 см и среди этих квадратиков случайным образом выбирают один. Какова вероятность, что расстояние от одной из сторон выбранного квадратика до границы листа составит не более 3 см?
. Квадратный лист бумаги со стороной 10 см разбивают на 100 квадратиков со стороной 1 см и среди этих квадратиков случайным образом выбирают один. Какова вероятность, что расстояние от одной из сторон выбранного квадратика до границы листа составит не более 3 см?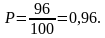
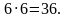 Вместо нахождения числа «интересующих нас» исходов опыта, найдём сначала число всех остальных исходов опыта – тех, в которых сумма выпавших очков больше 9.
Вместо нахождения числа «интересующих нас» исходов опыта, найдём сначала число всех остальных исходов опыта – тех, в которых сумма выпавших очков больше 9.

















