

Оглавление
Введение 3
История развития понятия функции. 6
Практическая часть. 19
Прикладные задачи по физике с математическим содержанием.…………....28
Заключение 32
Список использованной литературы 33
Введение
В современном мире математика и технические науки развиваются в тесном взаимодействии и сотрудничестве друг с другом. Сегодня трудно представить научно-техническую деятельность, где бы ни использовались фундаментальные исследования в области математики. Все технические инновации, которые окружают нас в повседневной жизни, есть результат плодотворного сотрудничества техники с математикой. Взаимодействие математических и прикладных дисциплин приводит к их двустороннему обогащению. С одной стороны, мы наблюдаем это в применении математического аппарата для решения технических задач. С другой стороны, инженерная практика в существенной мере определяет и стимулирует развитие самой математики. Такой симбиоз математики и технических наук уже весьма высоко зарекомендовал себя и открывает далекие перспективы в будущем.
Как известно, эффективному обучению во многом способствует решение задач с практическим содержанием. Потребность в использовании практических материалов математики диктуется тем, что возникновение, формирование и развитие математических понятий имеют своим источником ощущения и восприятия, а также и тем, что в познавательной деятельности имеет место тесная связь логических процессов мышления и чувственных восприятий. Поэтому обращение к примерам из жизни, окружающей обстановке облегчает возможность организовать учебную деятельность обучающихся и поддерживать их интерес к обучению. В то же время, бурное развитие математики и физики не могло не наложить определенного отпечатка на уровень развития и направление интересов учащихся. Интерес молодежи к технике, физике и математике растет с каждым днем.
Математика использует физические задачи для иллюстрации некоторых процессов, явлений и их исследования. Физики же не могут обойтись без аппарата математики. Функции – не исключение. Определенный круг вопросов, таких как физические законы, описывающие физические явления описываются с помощью различных математических функций. Поэтому довольно актуальным становится обучение математике (в частности изучение тем «Показательная и логарифмические функции», «Тригонометрические функции») через применение этих функций в физике.
Понятие функция является одним из основных в математике. Изучение этой понятия происходит на протяжение всего обучения в курсе средней школы, и постоянно знакомит обучающихся с новым терминами и зависимостями.
Анализ учебников и учебных пособий, содержащих материал по данной теме, показывает наличие разных мнений по поводу изложения этого достаточно сложного материала в определении содержания, необходимого для успешного усвоения и понимания основ функционального анализа.
Таким образом, актуальность темы работы обусловлена:
• необходимостью полноценного изучения важнейших элементов функционального анализа.
• недостаточной разработанностью методики преподавания этого материала с помощью использования физических моделей в курсе математики.
Исходя из вышесказанного, для исследования была выбрана тема «Применение функций для описания физических процессов и явлений».
Проблемой исследования является поиск путей применения функций для описания физических явлений и законов.
Объект исследования – процесс изучения функций использованием физических законов в курсе математики.
Предмет исследования – физические законы и явления при изучении функций в курсе математики.
Основные цели данной работы – собрать и систематизировать теоретический материал о различных функциях; рассмотреть использование функций в различных сферах жизнедеятельности.
Гипотеза: изучение функций, их свойств и графиков с помощью данного материала будет способствовать осознанному качественному усвоению обучающимися этого материала, развитию правильного представления об изучаемом понятии, его огромной значимости в физике.
Задачи исследования:
1. изучить и проанализировать научную, учебно-методическую и психолого-педагогическую литературу по теме исследования;
2. на основе анализа литературы предложить для изучения данной темы задачи на практическое применение функций в курсе математики.
Для достижения целей работы, проверки гипотезы и решения поставленных задач были использованы следующие методы:
1. изучение учебных пособий и методической литературы, содержащей этот материал.
В данной работе мы постараемся раскрыть связь математики и физики при решении физических задач. Рассмотреть применение функций для описания различных физических явлений.
История развития понятия функции.
Функция — роль и предназначение
Функция молотка — забивание гвоздей, а Центрального банка (не единственная) — выдача кредитов банкам помельче.
Вот мы и вернулись к первоначальному значению латинского слова “выполнять”. Молоток (выполняет работу) по забиванию гвоздей. Банк (выполняет работу) по выдаче кредитов. В обоих случаях есть и связь одного с другим и какое-то действие оправдывающее существование и молотка и банка.
В программировании функция — это код выполняющий определенную задачу. Подпрограмма которую можно “вызывать” (обычно много раз) для выполнения некой задачи. Вот пример из php:
Function sum($x,$y){return$x+$y;}
Даже не будучи программистом становится понятно, что функция по имени «sum» суммирует 2 переменные.
Итак функция, это зависимость, или работа, или предназначение… Зависит от контекста, но всегда есть минимум две сущности (может быть и больше) связанные каким-то правилом или законом, которые действуют одна на другую. Что-то с чем-то связано, кто-то на что-то оказывает влияние. Такая одновременно и простое и сложное, почти философское понятие, но встречается нам каждый день.
Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.
Идея функциональной зависимости восходит к древности. Так, вавилонские ученые (4-5тыс.лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r2. Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции - теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости.
П 
 уть к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы.
уть к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы.
К  роме того, у Декарта и Ферма (1601-1665) в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы; он систематически рассматривал лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы. В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени (называл в «флюентой»).
роме того, у Декарта и Ферма (1601-1665) в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы; он систематически рассматривал лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы. В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени (называл в «флюентой»).
В 
 «Геометрии» Декарта и работах Ферма, Ньютона и Лейбница понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями: ординаты точек кривых - функция от абсцисс (x); путь и скорость - функция от времени (t) и т.п.
«Геометрии» Декарта и работах Ферма, Ньютона и Лейбница понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями: ординаты точек кривых - функция от абсцисс (x); путь и скорость - функция от времени (t) и т.п.
Само слово «функция» (от латинского functio - совершение,выполнение) впервые было употреблено немецким математиком Лейбницем в 1673г. Швейцарский математик Иоганн Бернулли (1667-1748), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способ из этой переменной величины и постоянных». Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер (во «Введении в анализ бесконечного»). Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых 18 века по поводу того, что стоит понимать под функцией, внес французский математик Жан Батист Жозеф Фурье (1768-1830), занимавшийся в основном математической физикой.


 Дальнейшее развитие математической науки в 19 веке основывалось на общем определении функции Дирихле, ставшим классическим. В общем виде понятие обобщенной функции было введено французом Лораном Шварцем. В 1936 году, 28-летний советский математик и механик С.Л. Соболев первым рассмотрел частный случай обобщенной функции, включающей и дельта-функцию, и применил созданную теорию к решению ряда задач математической физики. Важный вклад в развитие теории обобщенной функции внести ученики и последователи Шварца - И.М. Гельфанд, Г.Е. Шилов и др.
Дальнейшее развитие математической науки в 19 веке основывалось на общем определении функции Дирихле, ставшим классическим. В общем виде понятие обобщенной функции было введено французом Лораном Шварцем. В 1936 году, 28-летний советский математик и механик С.Л. Соболев первым рассмотрел частный случай обобщенной функции, включающей и дельта-функцию, и применил созданную теорию к решению ряда задач математической физики. Важный вклад в развитие теории обобщенной функции внести ученики и последователи Шварца - И.М. Гельфанд, Г.Е. Шилов и др.
Что такое функция?
Разные ученые выдвигали разные мысли. Но мы хотим вас познакомить с одним определением: «Если даны числовое множество X и правило f, позволяющие поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят, что задана функция у = f(x) с областью определения Х; у = f(x) , хЄХ. При этом переменную х называют независимой переменной или аргумент, а переменную у- зависимой переменной.»
Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.
Функция – это не только математическое понятие, но и:
функция — работа, производимая органом, организмом; роль, значение чего-либо;
функция в математике — закон зависимости одной величины от другой;
функция — возможность, опция, умение программы или прибора;
функция — обязанность, круг деятельности;
функция персонажа в литературном произведении;
функция — вид подпрограммы в информатике социальная функция.
Каждая область знаний: физика, химия, биология, социология, лингвистика имеет свои объекты изучения, устанавливает свойства и, что особенно важно, взаимосвязи этих объектов.
В различных науках и областях человеческой деятельности возникают количественные соотношения, и математика изучает их в виде свойств чисел.
Математика создает условия для развития умения применять теоретические знания для решения практических задач, ориентироваться в окружающей нас действительности. Нам кажется, что функциональные зависимости могут касаться самых разнообразных явлений природы и окружающей среды. Каждому человеку в его повседневной практической деятельности приходится применять практические приемы геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков. Без конкретных математических знаний затруднено понимание и восприятие научных знаний, разнообразной социальной, экономической, технологической информации.
Свободное владение техникой построения графиков часто помогает решать многие задачи, а порой является естественным средством их решения. Математика является языком различных областей науки и нашей жизни.
Экологические проблемы являются глобальными проблемами человечества, всех стран независимо от размеров территории, численности населения, уровня экономического развития.
С функцией мы встречаемся каждый день.
Например:
каждый ученик в школе учится в определённом классе. Если обозначить через Х – множество учеников в школе, а через Y – множество классов, то можно сказать, что каждому элементу множества Х (т.е. каждому ученику) сопоставляется единственный элемент множества Y (т.е. тот класс, где данный ученик учится);
 пришли в магазин, покупаем конфеты. Пусть их цена 100 рублей. Сколько денег мы отдаем за 2кг? За 3кг? Говорят, что стоимость покупки есть функция от количества конфет;
пришли в магазин, покупаем конфеты. Пусть их цена 100 рублей. Сколько денег мы отдаем за 2кг? За 3кг? Говорят, что стоимость покупки есть функция от количества конфет;
 ежедневная температура на улице есть функция от времени. В одно и то же время температура не может принимать более одного значения и быть одновременно +5 и -10.
ежедневная температура на улице есть функция от времени. В одно и то же время температура не может принимать более одного значения и быть одновременно +5 и -10.
Способы задания функций.
Существует несколько способов задания функций:
аналитический,
графический,
табличный,
с помощью графов.
Аналитический способ.
Наиболее распространен аналитический способ задания функции, при котором функция задается формулой, устанавливающей, какие вычислительные операции надо произвести над х, чтобы найти у. Пример: у = к х; V = s h ; s = a b
Графический способ.
Распространен и графический способ задания функции. Графиком функции у=f(x), где х из множества Е, называется множество точек плоскости с прямоугольными координатами (х,у), где х из Е, у=f(x). Графический способ состоит в проведении линии (графика), у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Этот способ позволяет наглядно представить функциональную зависимость. Пример:
Табличный способ.
При табличном способе задания функция задается в виде таблицы, в которой для каждого значения аргумента указывается соответствующее ему значение функции. Табличный способ общеизвестен (таблица квадратов и таблица кубов натуральных чисел и т. д.). Этот способ сразу даёт числовое значение функции. В этом его преимущество перед другими способами.
Пример. Таблица квадратов чисел от 1 до 10:
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| х2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
С помощью графов.
В математике графом называют набор точек, некоторые из которых соединены линиями. Точки именуются вершинами графов, а отрезки- ребрами.
В курсе математики изучаются следующие
элементарные функции.
| Название функции | Формула функции | График функции | Название графика |
| Линейная | y = kx | 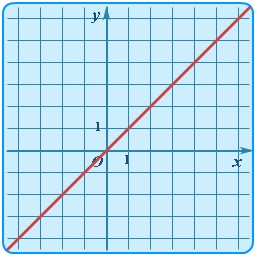
| Прямая |
| Линейная | y = kx + b | 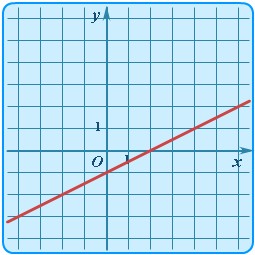
| Прямая |
| Квадратичная | y = x2 | 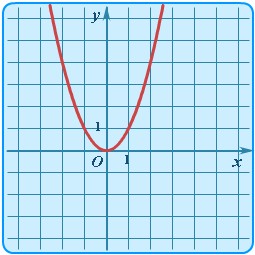
| Парабола |
| Квадратичная | y = ax2 + bx + c | 
| Парабола |
| Степенная | y = x3 | 
| Кубическая парабола |
| Степенная | y = x1/2 | 
| График функции
y = √x__ |
| Степенная | y = k/x | 
| Гипербола |
| Показательная | y = ex | 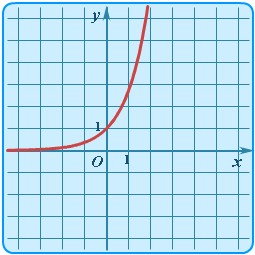
| Экспонента |
| Показательная | y = ax | 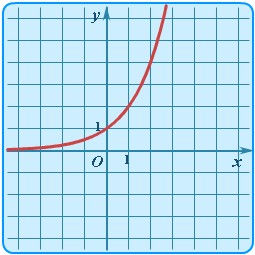
| График показательной функции |
| Показательная | y = ax | 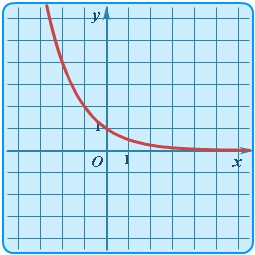
| График показательной функции |
| Логарифмическая | y = lnx | 
| График логарифмической функции |
| Логарифмическая | y = logax | 
| График логарифмической функции |
| Логарифмическая | y = logax | 
| График логарифмической функции |
| Синус | y = sinx | 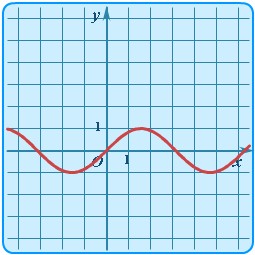
| Синусоида |
| Косинус | y = cosx | 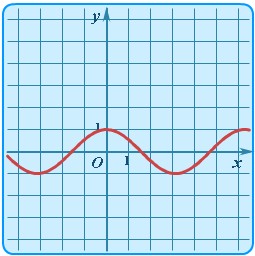
| Косинусоида |
| Тангенс | y = tgx | 
| Тангенсоида |
| Котангенс | y = сtgx | 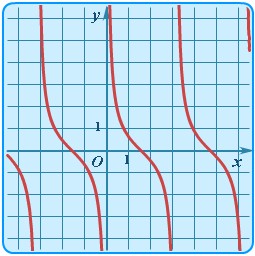
| Котангенсоида |
| Обратные тригонометрические функции. |
| Название функции | Формула функции | График функции | Название графика |
| Арксинус | y = arcsinx | 
| График арксинуса |
| Арккосинус | y = arccosx | 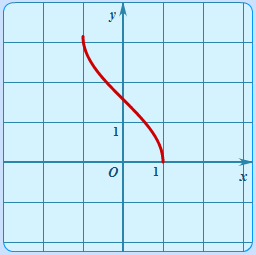
| График арккосинуса |
| Арктангенс | y = arctgx | 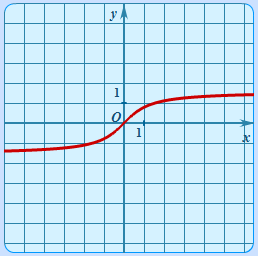
| График арктангенса |
| Арккотангенс. | y = arcctgx | 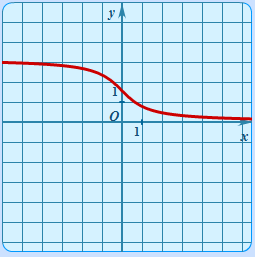
| График арккотангенса |
Практическая часть.
Рассмотрим применение вышеуказанных функций в физике.
Линейная y = kx + b и квадратичная функции y = ax2 + bx + c применяются в механике для описания равномерного и равноускоренного движений, для графического представления энергии.
.


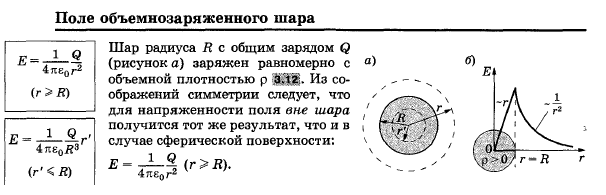
Прямая пропорциональность y = kx, линейная функция y = kx + b, обратная пропорциональность y = k/x применяются в молекулярной физике для описания изопроцессов, в электростатике – для описания электрического поля и для описания зависимости сопротивления от температуры, в квантовой физике для описания энергии электрона в атоме водорода.
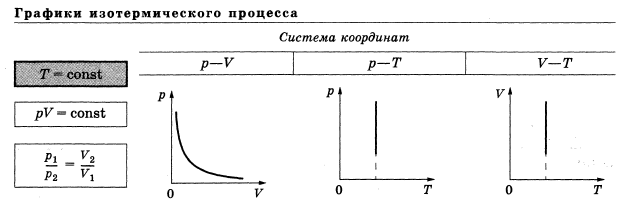
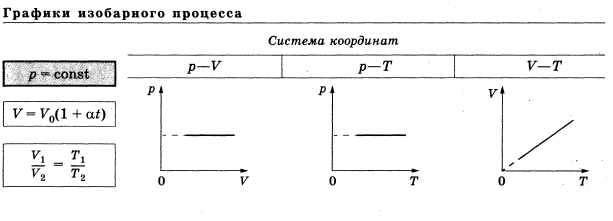
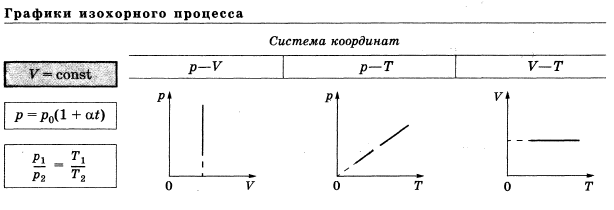



Квадратичная функции y = ax2, показательная функция (экспонента) y = ex применяются для описания распределения молекул газа по скоростям.

Показательная функция (экспонента) y = ex применяются для составления вольт-амперных характеристик, для описания токов замыкания и размыкания, для описания магнитных свойств вещества, для описания закона радиоактивного распада.





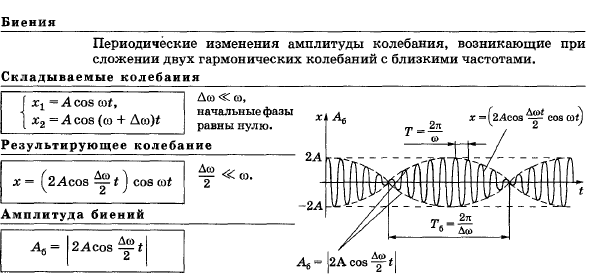
Тригонометрические функции y = sinx и y = cosx используются для описания колебательных процессов, для описания электромагнитных волн, для описания дифракции в оптике

Биения, как результат сложения колебаний.


Степенная функция используется при изучении p-n перехода в полупроводниках.

Мы рассмотрели малую часть применения математических функций для описания физических процессов и явлений.
Прикладные задачи по физике с математическим содержанием.
Решение задач на определение вида зависимости величин.
Все группы получают одинаковые задания. По окончании работы – самопроверка.
Зависимость модуля напряженности поля Е точечного заряда от расстояния r до него задана графиком:

Зависимость силы тока I от напряжения U для трех резисторов представлена на графике. Сопротивление какого резистора наибольшее?
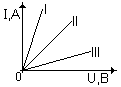
а) I;
б) II;
в) III;
г) сопротивления всех резисторов одинаковые.
Какой из графиков соответствует зависимости давления, оказываемого идеальным газом на стенки сосуда, от средней кинетической энергии поступательного движения молекул при постоянном объеме?

II. Решение и анализ физических задач с линейной зависимостью величин.
Решение задач в группах, затем представители от групп (поочередно) комментирует ход решения.
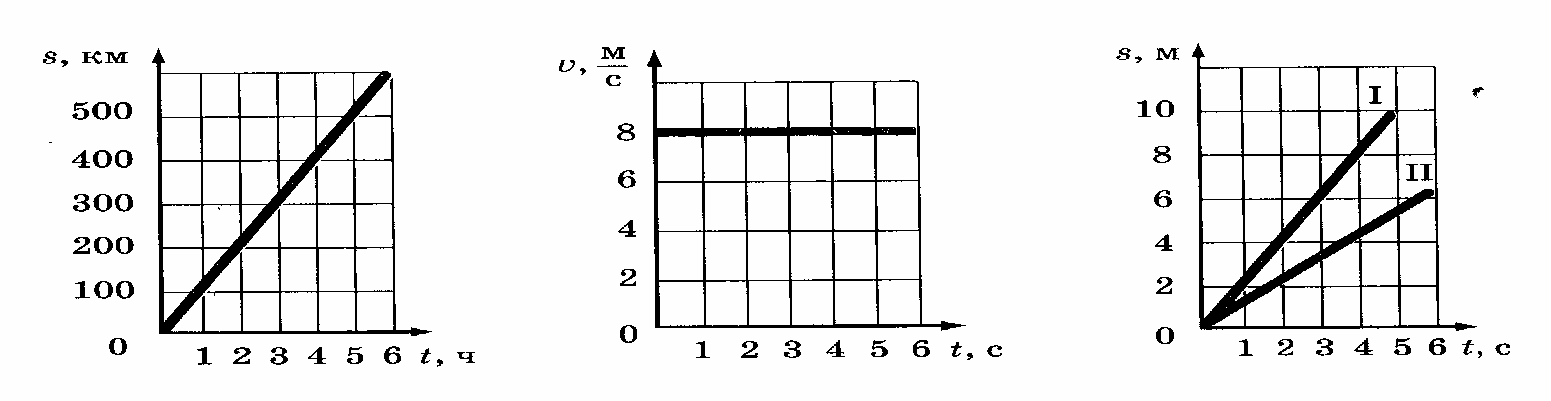
Задача 1. Автомобиль, выехавший из пункта А, в настоящее время находится от него в 120 км. На каком расстоянии S от пункта А будет находиться автомобиль через t ч, если он будет двигаться в том же направлении со скоростью 50 км/ч?
 [Решение: при равномерном движении тел зависимость между S и t задается формулой S=vot+So, т.е. выражается линейной функцией S=50t+120, где k=500. Функция возрастает, значит автомобиль будет удаляться от пункта А в течение всего времени движения. График – прямая линия, образующая с осью времени острый угол ?. tg? =vo. Чем больше скорость, тем больше угол наклона графика к оси времени, тем дальше от пункта А будет автомобиль через время t.]
[Решение: при равномерном движении тел зависимость между S и t задается формулой S=vot+So, т.е. выражается линейной функцией S=50t+120, где k=500. Функция возрастает, значит автомобиль будет удаляться от пункта А в течение всего времени движения. График – прямая линия, образующая с осью времени острый угол ?. tg? =vo. Чем больше скорость, тем больше угол наклона графика к оси времени, тем дальше от пункта А будет автомобиль через время t.]
Задача 2. Проанализировать зависимость кинетической энергии фотоэлектронов от частоты падающего излучения.
[Решение: явление фотоэффекта описывается уравнением Эйнштейна h? = Авых + Ек.
Отсюда Ек = h? – Авых. Зависимость между Ек и ? выражается линейной функцией вида
у = kx – b, где k = h = tg? угла наклона прямой к оси о?. Следовательно, 1) угол наклона ? графика зависимости Ек(?) одинаков для всех материалов tg? = h = const; 2) точка пересечения графика с осью о? определяется как -b/k, т.е. Авых/h = частота падающего  излучения, вызывающего фотоэффект, определяется только работой выхода электронов из данного вещества. С физической точки зрения можно рассматривать часть графика, соответствующую положительным значениям Ек.]
излучения, вызывающего фотоэффект, определяется только работой выхода электронов из данного вещества. С физической точки зрения можно рассматривать часть графика, соответствующую положительным значениям Ек.]
Задача 3. Проанализировать два адиабатных процесса при различных давлениях. Какое значение давления больше.

[Решение: из уравнения Менделеева-Клапейрона  для данной массы газа получим
для данной массы газа получим 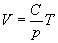 , где С=
, где С=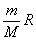 =const. Зависимость между V и Т выражается линейной функцией вида y = kx, где k = tg?, ? – угол наклона графика к оси температур. При увеличении р угловой коэффициент
=const. Зависимость между V и Т выражается линейной функцией вида y = kx, где k = tg?, ? – угол наклона графика к оси температур. При увеличении р угловой коэффициент  уменьшается, поэтому р2р1.]
уменьшается, поэтому р2р1.]
III. Использование степенной функции и ее графиков для решения физических задач.
Задача 1. Исследовать зависимость объема V идеального газа от давления р в изотермическом процессе.
[Решение: согласно закона Бойля-Мариотта при постоянной температуре Т произведение давления данной массы газа на его объем постоянно pV = k, где 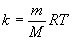 =const. Этот закон можно записать иначе:
=const. Этот закон можно записать иначе: 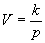 . Зависимость между p и V выражается степенной функцией вида
. Зависимость между p и V выражается степенной функцией вида 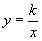 . Область определения и область значений функции – множество действительных чисел, за исключением нуля. График функции – гипербола. Значения p и V не могут быть отрицательными, поэтому область определения и область значений функции в данном случае есть множество положительных чисел, т.е. ветвь гиперболы расположена
. Область определения и область значений функции – множество действительных чисел, за исключением нуля. График функции – гипербола. Значения p и V не могут быть отрицательными, поэтому область определения и область значений функции в данном случае есть множество положительных чисел, т.е. ветвь гиперболы расположена
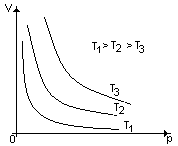 в I четверти. Если в уравнении
в I четверти. Если в уравнении 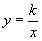
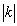 близок к нулю, то ветви гиперболы приближаются к осям координат; при k1 ветви гиперболы отодвигаются от осей. Таким образом, при низкой температуре Т1 ветви гиперболы ближе к осям координат, при Т2 Т1 ветви гиперболы отодвигаются от осей.]
близок к нулю, то ветви гиперболы приближаются к осям координат; при k1 ветви гиперболы отодвигаются от осей. Таким образом, при низкой температуре Т1 ветви гиперболы ближе к осям координат, при Т2 Т1 ветви гиперболы отодвигаются от осей.]
Задача 2. Исследовать зависимость силы тока I от сопротивления R участка цепи при постоянном напряжении U на этом участке.
Задача 3. Дан график скорости движения тела как функции времени. Построить эскизы графиков ускорения, перемещения и пройденного пути как функции времени.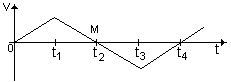
[Решение: судя по графику зависимости v(t) тело совершает неравномерное движение, описываемое уравнением v = v0 ± at или v = ± v0t + at, т.е. зависимость между v и t задана линейной функцией вида y = kx + b. Если ускорение а0, то скорость растет; если а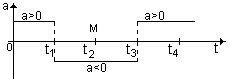
Зависимость перемещения от времени при равноускоренном движении задается функцией

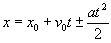 , т.е. степенной функцией вида y = ax2 ± c. На промежутке времени 0-t1
, т.е. степенной функцией вида y = ax2 ± c. На промежутке времени 0-t1
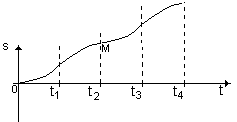
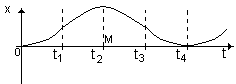 х? = v 0, значит функция возрастает. Так как в этот промежуток времени а 0, график представляет собой вогнутую параболу. На промежутке времени t1-t2 х? = v 0, значит функция возрастает, но а 2 (т.М) х? = v =0, значит т.М – стационарная. На промежутке времени t2-t3 х? = v 3-t4 х? = v 0, значит график – вогнутая парабола. В момент времени t4 функция опять начинает возрастать.
х? = v 0, значит функция возрастает. Так как в этот промежуток времени а 0, график представляет собой вогнутую параболу. На промежутке времени t1-t2 х? = v 0, значит функция возрастает, но а 2 (т.М) х? = v =0, значит т.М – стационарная. На промежутке времени t2-t3 х? = v 3-t4 х? = v 0, значит график – вогнутая парабола. В момент времени t4 функция опять начинает возрастать.
График зависимости пройденного пути от времени имеет тот же вид, что и график перемещения, а на промежутке времени t2-t4 - зеркальное отражение этого графика относительно т.М.
Заключение
Применение физических моделей, законов, явлений при изучении тех или иных функций, способствует осознанному качественному усвоению материала, развитию правильного представления об изучаемом понятии, его огромной значимости в различных науках, формированию мировоззрения, таких специальных качеств, как умение строить математические модели реальных процессов и явлений, исследовать и изучать их, а, следовательно, способствует развитию мышления, памяти, внимания и речи.
Список использованной литературы
Сигорский В.П. Математический аппарат инженера. – изд. 2-е, сте-реотип. – «Техника», 2000. – 753 с.
Амосов, А.А. Вычислительные методы для инженеров: учеб. пособие / А.А. Амосов, Ю.А. Дубинский, Н.А. Копченова; под общ. ред. - М.: Высш. шк., 1994. - 544 с.: ил
Письменный Д.Т. Конспект лекций по высшей математике. М.: Айрис-пресс, 2005. - 228 с.: ил.
Дьяченко М.И., Ульянов П.Л. Мера и интеграл. - М.: Издательство "Факториал Пресс", 2002. - 160с.
Камке Э. Интеграл Лебега-Стилтьеса. Перевод с немецкого Г.П. Сафроновой. Под ред. И.П. Натансона. - М.: Государственное издательство физ. - мат. литературы, 1959г.











 уть к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы.
уть к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы. роме того, у Декарта и Ферма (1601-1665) в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы; он систематически рассматривал лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы. В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени (называл в «флюентой»).
роме того, у Декарта и Ферма (1601-1665) в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы; он систематически рассматривал лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы. В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени (называл в «флюентой»).
 «Геометрии» Декарта и работах Ферма, Ньютона и Лейбница понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями: ординаты точек кривых - функция от абсцисс (x); путь и скорость - функция от времени (t) и т.п.
«Геометрии» Декарта и работах Ферма, Ньютона и Лейбница понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями: ординаты точек кривых - функция от абсцисс (x); путь и скорость - функция от времени (t) и т.п. 

 Дальнейшее развитие математической науки в 19 веке основывалось на общем определении функции Дирихле, ставшим классическим. В общем виде понятие обобщенной функции было введено французом Лораном Шварцем. В 1936 году, 28-летний советский математик и механик С.Л. Соболев первым рассмотрел частный случай обобщенной функции, включающей и дельта-функцию, и применил созданную теорию к решению ряда задач математической физики. Важный вклад в развитие теории обобщенной функции внести ученики и последователи Шварца - И.М. Гельфанд, Г.Е. Шилов и др.
Дальнейшее развитие математической науки в 19 веке основывалось на общем определении функции Дирихле, ставшим классическим. В общем виде понятие обобщенной функции было введено французом Лораном Шварцем. В 1936 году, 28-летний советский математик и механик С.Л. Соболев первым рассмотрел частный случай обобщенной функции, включающей и дельта-функцию, и применил созданную теорию к решению ряда задач математической физики. Важный вклад в развитие теории обобщенной функции внести ученики и последователи Шварца - И.М. Гельфанд, Г.Е. Шилов и др. пришли в магазин, покупаем конфеты. Пусть их цена 100 рублей. Сколько денег мы отдаем за 2кг? За 3кг? Говорят, что стоимость покупки есть функция от количества конфет;
пришли в магазин, покупаем конфеты. Пусть их цена 100 рублей. Сколько денег мы отдаем за 2кг? За 3кг? Говорят, что стоимость покупки есть функция от количества конфет; ежедневная температура на улице есть функция от времени. В одно и то же время температура не может принимать более одного значения и быть одновременно +5 и -10.
ежедневная температура на улице есть функция от времени. В одно и то же время температура не может принимать более одного значения и быть одновременно +5 и -10.












































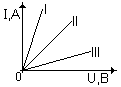

 [Решение: при равномерном движении тел зависимость между S и t задается формулой S=vot+So, т.е. выражается линейной функцией S=50t+120, где k=500. Функция возрастает, значит автомобиль будет удаляться от пункта А в течение всего времени движения. График – прямая линия, образующая с осью времени острый угол ?. tg? =vo. Чем больше скорость, тем больше угол наклона графика к оси времени, тем дальше от пункта А будет автомобиль через время t.]
[Решение: при равномерном движении тел зависимость между S и t задается формулой S=vot+So, т.е. выражается линейной функцией S=50t+120, где k=500. Функция возрастает, значит автомобиль будет удаляться от пункта А в течение всего времени движения. График – прямая линия, образующая с осью времени острый угол ?. tg? =vo. Чем больше скорость, тем больше угол наклона графика к оси времени, тем дальше от пункта А будет автомобиль через время t.] излучения, вызывающего фотоэффект, определяется только работой выхода электронов из данного вещества. С физической точки зрения можно рассматривать часть графика, соответствующую положительным значениям Ек.]
излучения, вызывающего фотоэффект, определяется только работой выхода электронов из данного вещества. С физической точки зрения можно рассматривать часть графика, соответствующую положительным значениям Ек.]
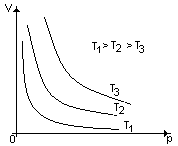 в I четверти. Если в уравнении
в I четверти. Если в уравнении 
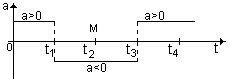
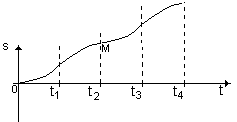
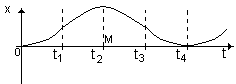 х? = v 0, значит функция возрастает. Так как в этот промежуток времени а 0, график представляет собой вогнутую параболу. На промежутке времени t1-t2 х? = v 0, значит функция возрастает, но а 2 (т.М) х? = v =0, значит т.М – стационарная. На промежутке времени t2-t3 х? = v 3-t4 х? = v 0, значит график – вогнутая парабола. В момент времени t4 функция опять начинает возрастать.
х? = v 0, значит функция возрастает. Так как в этот промежуток времени а 0, график представляет собой вогнутую параболу. На промежутке времени t1-t2 х? = v 0, значит функция возрастает, но а 2 (т.М) х? = v =0, значит т.М – стационарная. На промежутке времени t2-t3 х? = v 3-t4 х? = v 0, значит график – вогнутая парабола. В момент времени t4 функция опять начинает возрастать.

















