«Золотое сечение» и его пропорции в архитектуре»
Автор: Утешева Ксения
Ученица 11 класса МООУ «Санаторная
школа-интернат №2»
Научный руководитель:
Петрашова Валентина Николаевна
Учитель математики МООУ
«Санаторная школа-интернат №2»
Магнитогорск
Содержание.
1.Введение...................................................................................стр.3
2.Взаимосвязи математики и архитектуры:
2.1.Архитектура, с точки зрения математики..........................стр.4
2.2.Отношения архитектуры и математики.............................стр.5
2.3.Математические методы в архитектуре.............................стр.8
3.Практическое применение математики:
3.1.Золотое сечение.................................................................. стр. 9
3.2. «Золотое сечение» в строениях нашего города...............стр.11
3.3. Дом моей мечты.................................................................стр.12
3.4. Модель и макет дома моей мечты…………………..…..стр.13
4.Заключение..............................................................................стр.14
5.Литература...............................................................................стр.15
1. Введение.
Архитектура – удивительная область
человеческой деятельности. В ней тесно
переплетены и строго уравновешены
наука, техника и искусство.
А.В.Волошинов
Архитектура - это искусственная среда, воздвигнутая человеческими руками, является непременным условием существования и развития общества. Вот почему архитектура зарождается вместе с человеком и сопровождает человечество на всем его историческом пути. Роль математики в формировании «прочности» и «пользы» архитектуры очевидна.
Актуальность данного исследования состоит в том, что новейшие, современные открытия и исследования в математике способствуют скорейшему развитию архитектуры. Эти две дисциплины зависят друг от друга, взаимодействуют между собой.
Цели и задачи данной работы:
о вкладе математики в красоту архитектуры, то есть для нас архитектура будет, прежде всего, искусством;
об отношении друг к другу двух дисциплин, казалось бы, совершенно различной природы;
о влиянии друг на друга и о возможности анализа каждой из них методами другой;
попытаться спроектировать и сделать модель моего будущего дома, отвечающего пропорциям «золотого сечения».
о применении «золотого сечении», как математического понятия, в архитектуре.
Объектом исследования является взаимосвязь архитектуры и математики, эта связь нужна для того, чтобы архитекторы перестали смотреть на математику, как на нечто абстрактное, далекое от жизни и от архитектуры. Разработка эскиза и модели «дома моей мечты», соответствующая правилам «золотого сечения».
Гипотеза: математика, как составляющая архитектуры, как аппарат для качественного и гармоничного создания чертежей и впоследствии построения сооружений, всецело связана с архитектурой.
Математическая Энциклопедия определяет математику, как науку «о количественных отношениях и пространственных формах действительного мира». Архитектура – это совокупность зданий и сооружений, это пространство, созданное человеком и необходимое для его жизни и деятельности.
В работе эти две науки подразумеваются, как предмет исследования, анализа, сбора и систематизации информации.

2. Взаимосвязи математики и архитектуры.
2.1.Архитектура, с точки зрения математики.
Математические понятия носят абстрактный характер, а все построения архитектуры наоборот – имеют своей целью материальное воплощение, хотя на стадии постановки архитектурных задач и проектирования, сохраняют абстрактный, умозрительный характер. Более того, имеет хождение устойчивое словосочетание «бумажная архитектура», означающее проекты, которые по разным причинам не были воплощены. Несмотря на некую иронию этого термина, очевидно, что «бумажная архитектура», по крайней мере, на стадии обучения, тренировки, разработки вариантов, должна существовать. Она позволяет неизмеримо малыми, по сравнению со стоимостью строительства, средствами, получить, оценить, и промоделировать любую информацию о будущем объекте. Таким образом, можно сказать, что на стадиях постановки задач, разработки вариантов и проектирования архитектура ближе всего напоминает то, что обычно называют «чистой математикой».
По своему содержанию архитектура, как математика, имеет дело с иерархическими структурами. Аналогом неопределяемых понятий в ней служат вполне реальные предметы: кирпичи, элементы сборного железобетона и т. п. Из них строят дома, квартирные блоки, возводятся жилые и промышленные корпуса. В свою очередь, эти объекты образуют совокупности последующих уровней: ансамбли, кварталы, промышленные комплексы и т.п. Следующий уровень архитектурного творчества – поселки, города, промышленные зоны, районы и целые регионы. Завершает эту пирамиду некая гипотетическая архитектурная структура, включающая в себя целые страны, континенты и даже весь Земной Шар. Причем, на каждом уровне все архитектурные объекты и их объединения, кроме функциональной значимости, должны обладать целостностью, композиционной завершенностью и, что для архитектуры является не менее важным, быть красивыми, то есть вызывать у людей положительные эмоции.
Хотя развитие архитектуры, как и развитие математики, вплетено в общий поток человеческой истории, большую роль в обеих дисциплинах играют законы внутренней логики. Потому поведение и направление развития обеих дисциплин в будущем, в принципе, не предсказуемо и не подлежит планированию. В качестве примера, можно привести проекты «идеальных домов» и планы «городов будущего», созданные архитекторами античности и Возрождения, которые сейчас нам порой представляются наивными и даже - непрофессиональными.
Отметим также такую черту, свойственную и архитектуре, и математике, как, мы бы сказали, «благотворную» консервативность. Хотя архитектура, и в какой-то мере и математика, иногда, особенно на переломе эпох, как бы, «стесняются» своего прошлого, пытаясь освободиться от наследия предыдущего, ни та, ни другая дисциплина не могут существовать без преемственности, не опираясь на опыт предшествующих поколений, на выработанные ранее понятия, образы, приёмы, символику и т. п.
Нельзя не сказать о сходстве обеих дисциплин в таком «философском» аспекте, как отношение математических и архитектурных построений к жизни, то есть – непосредственно к бытию. Имеются в виду неизбежные различия между идеальными понятиями и теми природными или искусственными объектами, которым они должны соответствовать. Действительно, ни один даже самый «тонкий и прямой», материальный стержень, на самом деле не является отрезком прямой линии, каким его представляет себе математик. Аналогично, и самое совершенное, с точки зрения строительства, сооружение в каких-то деталях всегда будет отличаться от того идеального образа, который возник в мозгу архитектора. Важно только, чтобы сумма всех этих отличий и отклонений не превышала того порога, за которым теряется идеальный образ, то есть, цель данного построения.
2.2.Отношения архитектуры и математики.
Следует отметить, что потребности зарождающегося строительства и, возникшей вслед за ним архитектуры явились одним стимулов, благодаря которым возникла и сделала первые шаги математика. Это, в частности, нашло отражение в названии одной из старейших разделов математики – геометрии, что означает землемерие. Действительно, с задач землемерия расстояний, площадей земельных участков, нахождения закономерностей между линейными размерами и площадями различных фигур, на предметном уровне, и начиналась геометрия – важный и самый наглядный раздел математики.

Напомним, что в древности математика, как и архитектура, относилась к искусствам. Образование человека считалось неполным, если он, наряду с философией, поэзией, музыкой и т.п., не овладевал современной ему математикой, не умел ставить и решать задачи, доказывать теоремы. Великие философы древности Аристотель, Платон и были хорошими математиками, имена некоторых, например, Пифагора, Евклида, Фалеса и других известны в наше время, благодаря их выдающимся математическим открытиям (Пифагоровы числа, постулаты Евклида, теорема Фалеса). Несомненно, и то, что математика, в своём развитии, оказала определённое влияние на архитектуру. Ещё в древности были открыты и использовались в архитектуре такие ключевые понятия математики, как общая мера архитектурного объекта (модуль), несоизмеримого отношения и – другие. Математики разработали много методов получения этого отношения на практике. Простейшие поверхности, образованные движением прямой в пространстве и называемые линейчатыми поверхностями – цилиндры и конусы,- были известны давно. Еще древние римляне сооружали цилиндрические своды. А существуют ли другие линейчатые поверхности? Ответ на этот вопрос архитекторам подсказали математики, которые обнаружили еще два типа линейчатых поверхностей:
однополостный гиперболоид: �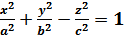 �
�
гиперболический параболоид: �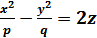 �
�
Канонические уравнения этих поверхностей легко представить в виде � �, �
�, �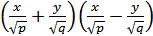 �, откуда и видно, что они образованны двумя семействами прямых в пространстве (в уравнение прямой переменные x,y,z входят только в первых степенях).
�, откуда и видно, что они образованны двумя семействами прямых в пространстве (в уравнение прямой переменные x,y,z входят только в первых степенях).
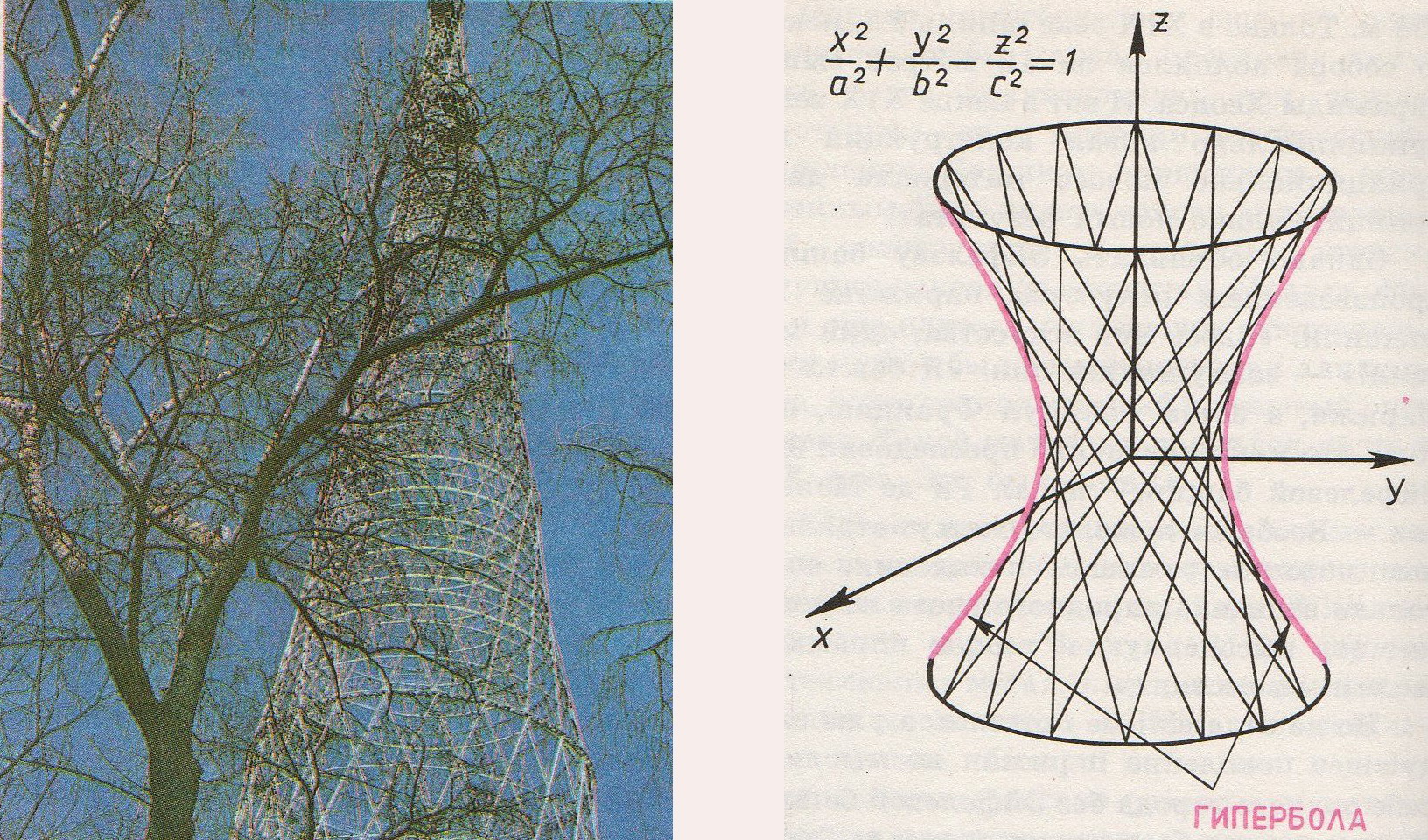
Архитекторы воспользовались открытием математиков. Форму однополостного гиперболоида имеют градирни – устройства для охлаждения воды атмосферным воздухом. Линейчатое свойство однополостного гиперболоида положено в основу конструкции Шаболовской радиобашни в Москве, построенной по проекту замечательного русского советского инженера, почетного академика В.Г.Шухова. Башня Шухова состоит из нескольких поставленных друг на друга частей однополостных гиперболоидов, причем каждая часть сделана из двух семейств прямолинейных балок, соединенных в точках пересечения(см. рис.).
Если однополостный гиперболоид отдает должное «пользе» в архитектуре, то гиперболический параболоид (архитекторы называют его красивым сокращенным именем гипар) благодаря своей выразительной и элегантной форме служит «красоте». Архитектурные возможности гипаров открыл инженер Феликс Кандела – испанский патриот, сражавшийся против фашистской диктатуры Франко, вынужденный эмигрировать в Мексику. Кандела с блеском продемонстрировал выразительные свойства гипаров на различных сооружениях – от промышленных зданий до ресторанов, ночных клубов и церквей.
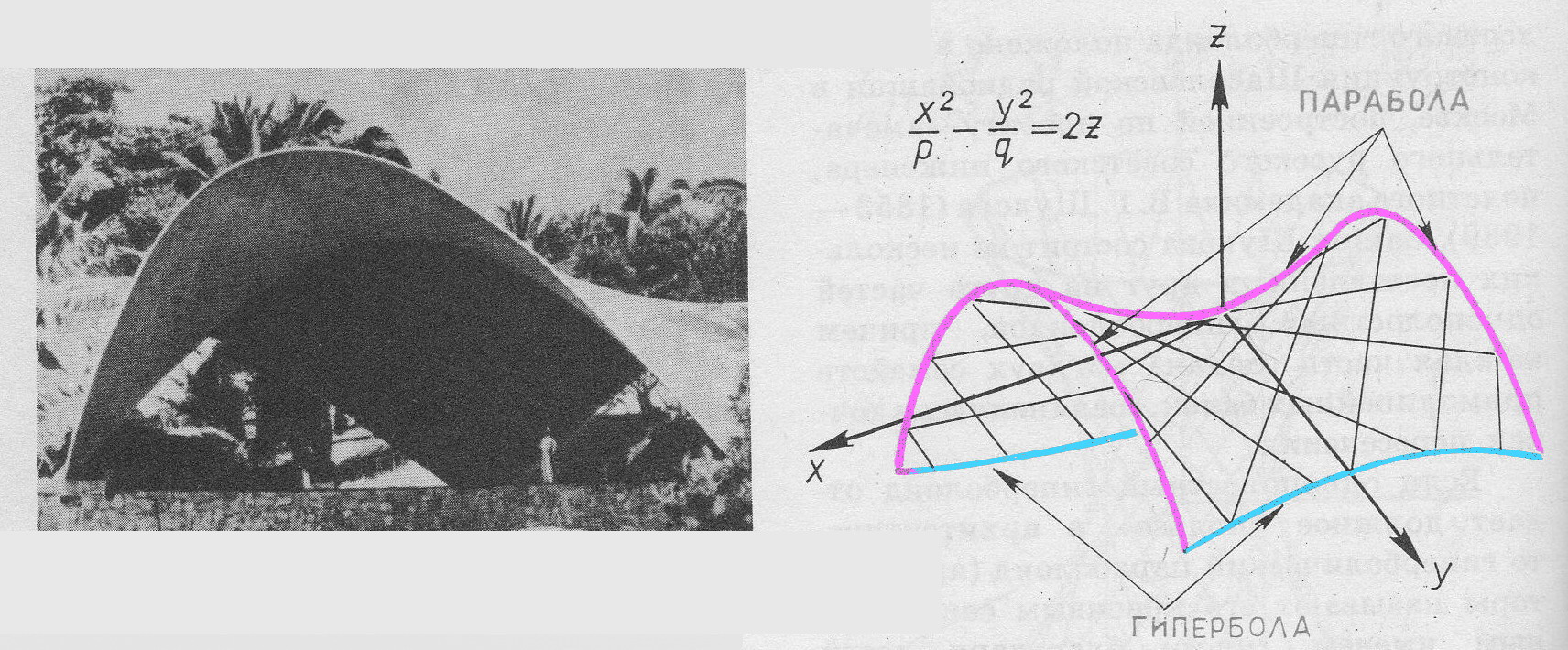
2.3.Математические методы в архитектуре.
Использовались и другие математические факты. Например: квадрат имеет наименьший периметр из всех прямоугольников, охватывающих площадь определённой величины; для любого треугольника всегда можно найти вписанную и описанную окружности; метод деления отрезка на любое число равных между собой отрезков – и многое другое. Активно применялись в архитектурной практике и такие понятия прикладной математики, как масштаб, единицы измерения, приближенные вычисления.
С другой стороны, можно проследить и влияние архитектуры на развитие математики в целом. Действительно, для осуществления всё более сложных и в то же время экономичных построек всегда требовалось предварительное планирование, разработка более тонких математических приёмов и моделей, использование более совершенных точных вычислительных методов. Всё это, в ответ на запросы архитектурной практики разрабатывала теоретическая и прикладная математика.
Применение математических методов в архитектуре в наше время осуществляется по разным направлениям. Прежде всего, используются геометрические формы, которые не употреблялись ранее. Примеров можно приводить сколь угодно много. Это и гиперболоиды вращения, и перекрытия больших помещений самонесущими поверхностями; использование мембран и оболочек, применение винтовых поверхностей – и многое другое.
Другое направление – математическое моделирование, в том числе – и использование ЭВМ для расчета поведения сложных архитектурных и градостроительных объектов и систем во времени. Применение этих методов в архитектуре позволяет избегать ошибок при строительстве, более рационально расходовать ресурсы, при минимальных затратах добиваться более значительных результатов.
Упомянем и о таком деликатном приложении математики к архитектуре, как разработка методов по оценке эстетического воздействия сооружения на человека. Несмотря на трудности, возникающие при формализации таких задач, и, несмотря на скептическое отношение некоторых архитекторов и искусствоведов к такой идее, поисковые работы в этом направлении ведутся, а результаты накапливаются и систематизируются.
3.Практическое применение математики.
3.1.Золотое сечение.
Большое влияние на архитектуру, на эстетику и на всё искусство оказало, так называемое, отношение «Золотого сечения». Для дальнейшего повествования о золотом сечении, поговорим о пятиконечной звезде. Ей около 3000 лет. Её первые изображения донесли до нас вавилонские глиняные таблички. Рассмотрим свойства звездчатого пятиугольника. Прежде всего, заметим, что уже первый этап его построения – деление окружности на пять равных частей – представляет собой прекрасный пример «обретения неочевидной истины». В самом деле, в то время как деление окружности на три, четыре и шесть равных частей не представляет затруднений, разделить окружность на пять равных частей не так-то просто. Вот почему задача о пятикратном делении окружности подробно разбирается в таких великих сочинениях, как «Начала» Евклида, «Альмагест» Птолемея, «Руководство к измерению…» Дюрера.
Итак, пусть окружность разделена на пять равных частей. Соединяя последовательно точки деления, получим правильный пятиугольник, диагонали которого образуют пятиконечную звезду. Легко видеть, что внутри этой звезды вновь образуется правильный пятиугольник, диагонали которого дают новую звезду, и так далее. Рассмотрим равнобедренный треугольник АВС, в котором � �, �
�, � � (как вписанные в окружность углы, опирающиеся на дуги в 72�
� (как вписанные в окружность углы, опирающиеся на дуги в 72� � (360�
� (360� �:5) и 144�
�:5) и 144� � соответственно). Но D = 36�
� соответственно). Но D = 36� �, поэтому СD является биссектрисой в треугольнике АВС и отсекает от него r BCD �
�, поэтому СD является биссектрисой в треугольнике АВС и отсекает от него r BCD �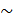 � r АВС. Из подобия этих треугольников имеем АВ : ВС = ВС : DB. Учитывая, что ВС = CD = AD, приходим к пропорции
� r АВС. Из подобия этих треугольников имеем АВ : ВС = ВС : DB. Учитывая, что ВС = CD = AD, приходим к пропорции
�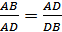 �
�
То есть «целое» (АВ) так относится к большей части (AD), как большая часть к меньшей (DB). Иначе говоря, точка D делит отрезок АВ в золотом сечении.
Принимая сторону исходного правильного пятиугольника за единицу АF = АD = 1, полагая DB = х и, следовательно, АВ = 1 + х, затем приходим к уравнению при а = 1:
�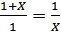 � ð �
� ð �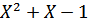 �=0
�=0
Это уравнение имеет единственный корень
�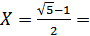 � φ
� φ
Поскольку 1 – φ =�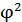 �, то мы окончательно находим: х = DB = AE = ... = φ, AD = DC = CB = AF = ... = 1, ED = EG = ... = 1 – φ =�
�, то мы окончательно находим: х = DB = AE = ... = φ, AD = DC = CB = AF = ... = 1, ED = EG = ... = 1 – φ =�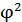 �.
�.
Повторяя наши рассуждения для треугольника DGH, в котором DG = φ, легко видеть, что стороны внутренней звезды будут равны �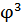 �, а стороны её внутреннего правильного пятиугольника – �
�, а стороны её внутреннего правильного пятиугольника – �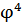 �. И так далее.
�. И так далее.
Таким образом, последовательность правильных пятиугольников и вписанных в них звезд образует ряд золотого сечения при а = 1: �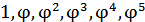 �, … , причем стороны правильных пятиугольников образует ряд четных степеней: �
�, … , причем стороны правильных пятиугольников образует ряд четных степеней: � �, … , а стороны звезд – ряд нечетных степеней: �
�, … , а стороны звезд – ряд нечетных степеней: �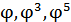 �, … .
�, … .
Такой ряд является геометрической прогрессией. Однако из бесконечного множества геометрических прогрессий ряд отличается уникальным свойством, называемым аддитивным: сумма двух соседних членов ряда равна следующему члену ряда.

Хочется закончить разговор о золотом сечении одним примером, показывающим, насколько органично входит оно в архитектурные пропорции. В качестве примера рассмотрим пропорциональный строй одной из жемчужин древнерусской архитектуры – храма Василия Блаженного в Москве. За «целое» а = 1 принята высота храма. Пропорции храма определяются восемью членами ряда золотого сечения: �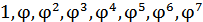 �. Многие из членов ряда неоднократно повторяются в пропорциях этого затейливого архитектурного сооружения, но всегда благодаря аддитивному свойству золотого сечения я уверена в том, что части сойдутся в целое, то есть �
�. Многие из членов ряда неоднократно повторяются в пропорциях этого затейливого архитектурного сооружения, но всегда благодаря аддитивному свойству золотого сечения я уверена в том, что части сойдутся в целое, то есть � � и так далее. Таким образом, аддитивное свойство золотого сечения делает эту геометрическую пропорцию единственной и неповторимой.
� и так далее. Таким образом, аддитивное свойство золотого сечения делает эту геометрическую пропорцию единственной и неповторимой. 
3.2. «Золотое сечение» в строениях нашего города.


Пропорции «Золотого Сечения» исходят из строения Мироздания, поэтому все известные принципы гармонии основаны именно на этом «сечении».
Доказывать это излишне, так как каждый по собственному опыту знает, что в старинных зданиях, построенных в пропорциях «золотого сечения», лучше живется и легче дышится, чем в современных многоэтажных железобетонных коробках. Как, например, классическая музыка вызывает прилив сил, в отличии от современной рок- и поп-музыки.
Весь город можно разделить на государственные многоэтажные дома и частные секторы. Редко в Магнитогорске можно увидеть многоэтажные жилые дома в которых проглядывается пропорция золотого сечения, но такие дома существуют. В то же время, "многоэтажки" приобретают красоту благодаря аркам, колоннам и подобным сооружениям и достройкам.


В домах левобережья красоту придают колонны, арки, лепнина и пилястры.
3.3. Дом моей мечты.
Всё чаще и чаще в наши дни люди стремятся купить свой дом - уютный и надежный, родной. Все хотят иметь свое пространство, в которое никто посторонний не будет вторгаться. Жители больших городов - люди особые, они ежедневно и помногу вторгаются в жизненное пространство друг друга. Их общение по большей части вынужденное - как общение зверей в тесной клетке. Свой дом должен быть не только красивым, но и комфортным. Люди, покупающие себе дом, либо те, кто строит сам, могут учесть все эти критерии и другие свои требования. В отличии от них, те, кто покупает квартиру в большом доме, лишаются многого.

Рассмотрев, один из предлагаемых фирмой частных домов, можно найти ряд пропорций «золотого сечения». За единицу можно принять: высоту дома, высоту парадного входа и высоту балкона.
3.4. Модель и макет дома моей мечты.
Одной из составляющих практической части работы, является макет «моего будущего» дома. Так как мы пока не архитекторы, модель выглядит довольно просто, но в его пропорциях четко виден ряд членов «золотого сечения».
Макет создан для того, чтобы научиться видеть пропорции «золотого сечения». Если самому попробовать применить математические знания при моделировании дома, то в обычной, повседневной жизни можно найти в окружающих нас зданиях, исторических и современных постройках и пропорции золотого сечения, и другие математические понятия применяемые в архитектуре.
З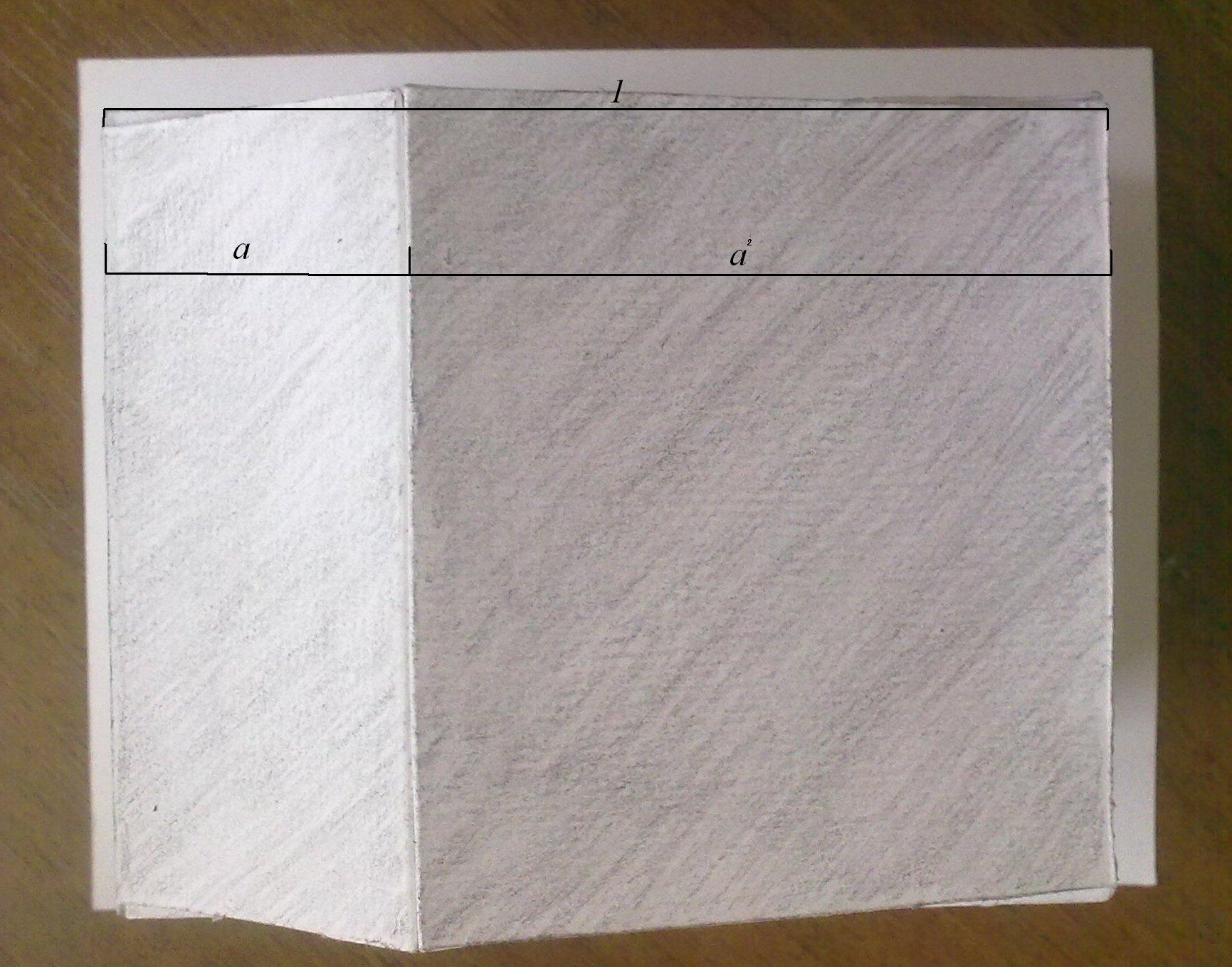 а единицу принята длина крыши, длина крутого малого ската 1/3 всей длины крыши, т.е. «a». Длина пологого ската равна 2/3 всей длины.
а единицу принята длина крыши, длина крутого малого ската 1/3 всей длины крыши, т.е. «a». Длина пологого ската равна 2/3 всей длины.
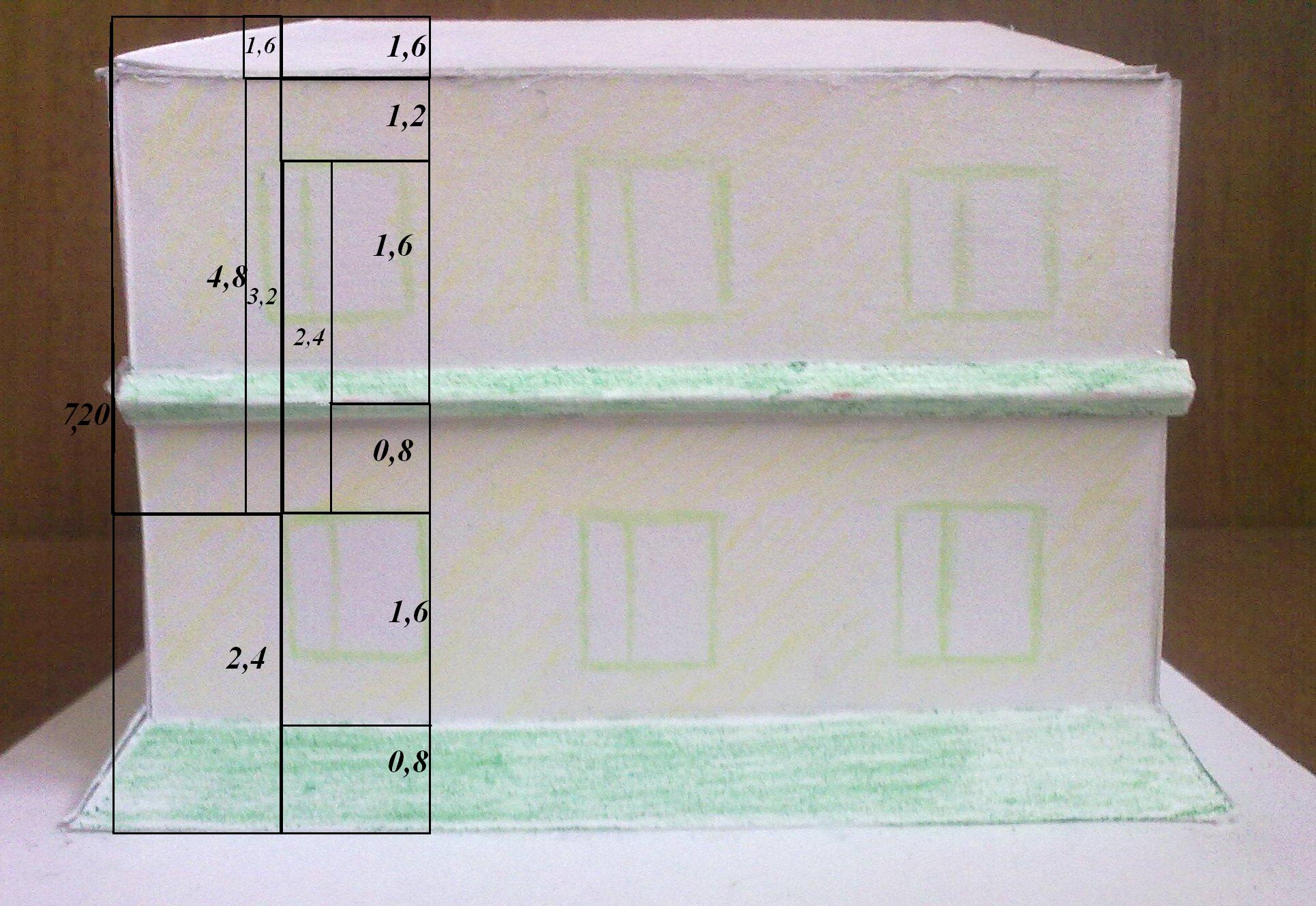
Высота дома равна 7,2 метра.
По принципу «золотого сечения» делим всю высоту на 3 части. Две третьих из трех частей равны 4,8 метра, одна третья равна 2,4 метра. По этому же принципу делятся и остальные составляющие дома.
4.Заключение.
Всё сказанное убеждает нас в том, что архитектура и математика, являясь соответствующими проявлениями человеческой культуры, на протяжении веков активно влияли друг на друга. Они давали друг другу новые идеи и стимулы, совместно ставили и решали задачи. По сути, каждую из этих дисциплин можно рассматривать существенным и необходимым дополнением другой.
Следует, однако, предостеречь от другой крайности – элементов «фетишизации» математики. Некоторые люди считают, что «Математика, способна решить всё!». На самом деле – не всё и не всегда. Математика никогда не сможет, например, ответить на основные вопросы бытия, определить, что такое искусство, красота и – многое другое.
Не надо также забывать, что математика решает только поставленные задачи, а поставлены они должны быть корректно.
Необходимо помнить и главный принцип математики: «Нельзя объять бесконечное (время, пространство, информацию и т.д.), но можно досконально (на самом деле – с любой степенью точности) изучить строение материальных объектов и поведение процессов и явлений в малых областях».
И архитекторы в своей профессиональной деятельности могут и должны использовать не только вычислительный аппарат математики, но и применять её методологию, её доказательную строгость, её логику и, конечно, её своеобразную, математическую красоту.
Изучив эти две дисциплины, приходим к выводу:
1) что очевиден вклад математики в красоту архитектуры, прежде всего, как искусства;
2) что есть возможности анализа каждой из науки методами другой.
3) что математика, как аппарат для качественного и гармоничного создания чертежей и впоследствии построения сооружений, всецело связана с архитектурой.
4) что, если человек хочет жить комфортно и легко дышать в своем доме, то нужно построить свой дом, отвечающий пропорциям «золотого сечения».
 БАРСЕЛОНА
БАРСЕЛОНА





5.Литература.
1.Большой Российский энциклопедический словарь.-М.:Большая Б79 Российская энциклопедия,2006.-1887:ил.
2.Гликин Я.Д. Методы архитектурной гармонии.-Л.: Стройиздат, 1979.
3.Гримм Г.Д. Пропорциональность в архитектуре.-Л.; М.: ОНТИ,1935.
4.Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение.-М.:Стройиздат, 1990
5.http.//www.edic.ru. Большой энциклопедический и исторический словари он-лайн.
6. http.//www.school.edu.ru. Российский образовательный портал.
7. htt.//www.nips.riss-telecom.ru/poly/
8. htt.//www.photoline.ru/tcomp 1.htm
9.Математика: Школьная энциклопедия.-М.:Большая Российская энциклопедия, 2003.-М34 528с.:ил.
10.Волошин А.В. Математика и искусство.- М.: Просвещение, 1992. – 335 с.: ил.
20









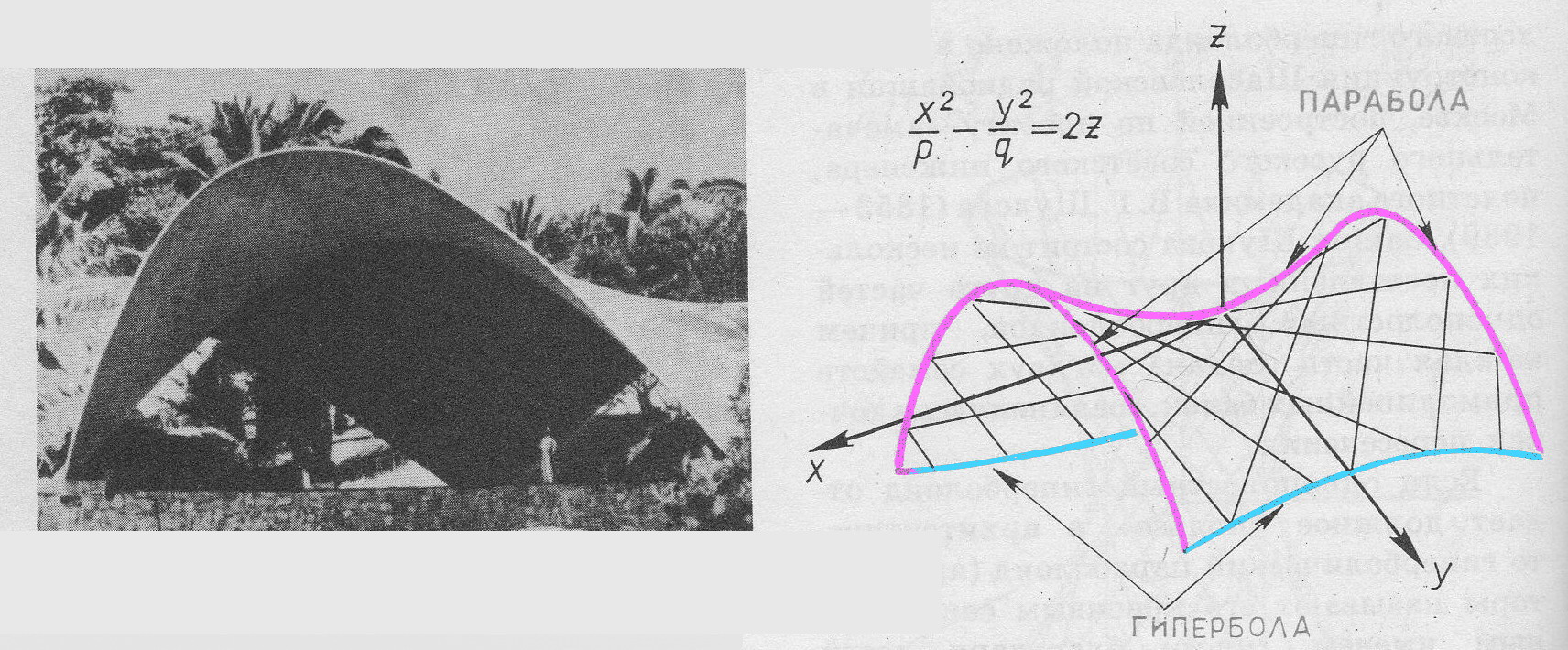








 а единицу принята длина крыши, длина крутого малого ската 1/3 всей длины крыши, т.е. «a». Длина пологого ската равна 2/3 всей длины.
а единицу принята длина крыши, длина крутого малого ската 1/3 всей длины крыши, т.е. «a». Длина пологого ската равна 2/3 всей длины.
 БАРСЕЛОНА
БАРСЕЛОНА





















