МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ ДИНАМИЧЕСКИХ СИСТЕМ
Устойчивость характеризует одну из важнейших черт поведения систем и является фундаментальным понятием, используемым в физике, биологии, технике, экономике. Понятие устойчивости применяется для описания постоянства какой-либо черты поведения системы, понимаемого в весьма широком смысле. Это может быть постоянство состояния системы (его неизменность во времени) или постоянство некоторой последовательности состояний, «пробегаемых» системой в процессе ее движения, или постоянство числа определенного биологического вида, живущего на земном шаре, и т. п.
Под устойчивостью понимается свойство системы возвращаться к равновесному состоянию или циклическому режиму после устранения возмущения, вызвавшего нарушения последних.
Устойчивость есть категория, относящаяся, прежде всего, к собственным движениям системы, порождаемым начальными условиями (возмущениями) и внутренними свойствами системы, но не внешними воздействиями.
Состояние равновесия, в которое система способна возвращаться, называют устойчивым состоянием равновесия.
Состояние устойчивости (устойчивое состояние) - это такое равновесное состояние системы, в которое, она возвращается после снятия возмущающих воздействий.
Простейшим примером устойчивой системы может служить маятник с трением, колеблющийся по затухающему закону. Другими примерами устойчивых систем могут служить шарик в ямке, пассивная электрическая цепь. Переходная функция устойчивой системы с течением времени монотонно или колебательно стремится к некоторому постоянному значению.
Для неустойчивой системы характерна обратная тенденция. Если ее вывести из состояния равновесия, то сама она в это состояние не возвращается. Существует несколько определений устойчивости, в частности, различают устойчивость в малом и большом, устойчивость по Ляпунову, асимптотическую устойчивость и т. д. Примеры неустойчивых систем – перевернутый маятник, шарик на вершине горы, карандаш, стоящий на острие.
Во многих случаях не так легко ответить на вопрос, является ли система устойчивой. С математической точки зрения удобнее говорить не об устойчивости самих систем, а об устойчивости соответствующих дифференциальных уравнений. Решение устойчивых дифференциальных уравнений со временем стремится к нулю. Так, уравнение, описывающее движение маятника
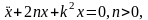
устойчиво, так как его решение
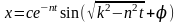
асимптотически стремится к нулю при 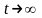 .
.
Аналогичное уравнение карандаша, стоящего на острие 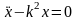 , неустойчиво, так как второе слагаемое в решении
, неустойчиво, так как второе слагаемое в решении 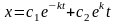 неограниченно возрастает со временем.
неограниченно возрастает со временем.
1. Постановка задачи
Рассмотрим систему:
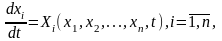 (2.1)
(2.1)
Предположим, что правые части системы (2.1), т.е. функции 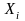 , непрерывны в некоторой области
, непрерывны в некоторой области 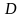 , который может совпадать со всем
, который может совпадать со всем 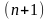 - мерным пространством переменных
- мерным пространством переменных 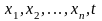 . Будем считать, что, кроме того, для системы (2.1) в области
. Будем считать, что, кроме того, для системы (2.1) в области 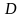 выполнены условия существования и единственности решения
выполнены условия существования и единственности решения
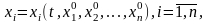 (2.2)
(2.2)
удовлетворяющего начальным условиям
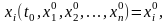 (2.3)
(2.3)
где 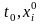 - некоторые числа из области
- некоторые числа из области 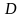 . Будем предполагать, что решение (2.2) определено для любого значения
. Будем предполагать, что решение (2.2) определено для любого значения 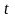 , в этом случае оно называется продолжаемым.
, в этом случае оно называется продолжаемым.
Правые части системы (2.1) можно рассматривать как проекции переменного вектора скорости 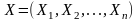 , а величину
, а величину 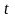 - как время. Тогда система (2.1) описывает закон движения начальной точки
- как время. Тогда система (2.1) описывает закон движения начальной точки 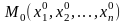
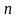 - мерного фазового пространства по траектории
- мерного фазового пространства по траектории 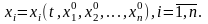
Запишем систему (2.1) в векторной форме:
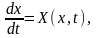 (2.4)
(2.4)
где 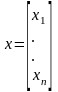 - вектор-столбец размерности
- вектор-столбец размерности  ;
;
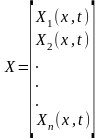 является вектором скорости.
является вектором скорости.
Решением системы (2.4) называется векторная функция
.
Через  обозначим норму вектора, который будем считать совпадающей с евклидовой длиной вектора.
обозначим норму вектора, который будем считать совпадающей с евклидовой длиной вектора.
. (2.5).
2. Определение устойчивости.
Уравнения возмущенного движения
Рассмотрим систему дифференциальных уравнений
 . (2.6)
. (2.6)
Выделим некоторое решение  системы (2.6) и назовем его невозмущенным движением.
системы (2.6) и назовем его невозмущенным движением.
Определение. Движение  называется устойчивым в смысле Ляпунова, если для любого
называется устойчивым в смысле Ляпунова, если для любого  существует
существует  такое, что из неравенства следует неравенство
такое, что из неравенства следует неравенство  при любых
при любых  . Здесь через
. Здесь через  обозначено любое другое решение системы (2.6), определяемое начальными условиями
обозначено любое другое решение системы (2.6), определяемое начальными условиями  . (рис. 2.1.).
. (рис. 2.1.).
Рис. 2.1.
Определение. Движение  называется неустойчивым, если существует
называется неустойчивым, если существует  и решения
и решения  такие, что для любого
такие, что для любого  при найдется
при найдется такое, что
такое, что  (рис. 2.2).
(рис. 2.2).
Рис. 2.2.
Определение. Движение  называется асимптотчески устойчивым в смысле Ляпунова, если оно устойчиво в смысле Ляпунова и существует такое положительное число
называется асимптотчески устойчивым в смысле Ляпунова, если оно устойчиво в смысле Ляпунова и существует такое положительное число  , что при будем иметь (рис. 2.3)
, что при будем иметь (рис. 2.3)
. (2.7)
Рис. 2.3.
Определение. Если движение  устойчиво по Ляпунову и соотношение (2.7) справедливо для решения
устойчиво по Ляпунову и соотношение (2.7) справедливо для решения  , определяемых любыми начальными условиями, то говорят, что движение
, определяемых любыми начальными условиями, то говорят, что движение  асимптотически устойчиво при любых начальных данных ( или асимптотически устойчиво в целом; рис 2.4).
асимптотически устойчиво при любых начальных данных ( или асимптотически устойчиво в целом; рис 2.4).
Рис.2.4.
Произведем в системе (2.6) замену искомой функции  функцией
функцией  :
:
 .
.
Новая система будет иметь вид:
.
Введя обозначение , получим систему:
 , (2.8)
, (2.8)
где  при
при  .
.
Система (2.8) определяет дифференциальные уравнения возмущенного движения. Движение  переходит при рассматриваемой замене переменных в состояние равновесия
переходит при рассматриваемой замене переменных в состояние равновесия  новой системы, а задача устойчивости движения
новой системы, а задача устойчивости движения  - в задачу устойчивости нулевого решения системы (2.8)
- в задачу устойчивости нулевого решения системы (2.8)  .
.
Определение. Решение  системы (2.8) называется устойчивым в смысле Ляпунова, если для любого
системы (2.8) называется устойчивым в смысле Ляпунова, если для любого  существует
существует  такое, что из неравенства
такое, что из неравенства  следует неравенство
следует неравенство  при любых
при любых  .
.
Определение. Нулевое решение называется асимптотчески устойчивым в смысле Ляпунова, если оно устойчиво в смысле Ляпунова и существует такое положительное число  , что при
, что при  выполняется условие . Область
выполняется условие . Область  называется областью притяжения нулевого решения. Если эта область охватывает все фазовое пространство
называется областью притяжения нулевого решения. Если эта область охватывает все фазовое пространство  , нулевое решение системы (2.8) называется асимптотически устойчивым в целом.
, нулевое решение системы (2.8) называется асимптотически устойчивым в целом.
На рис. 2.5, 2.6 дается геометрическая интерпретация данных определений устойчивости в случае двумерных векторов  ,т.е. описывается поведение траекторий движения
,т.е. описывается поведение траекторий движения  на фазовой плоскости.
на фазовой плоскости.
Рис. 2.5. Рис. 2.6.
Рис. 2.7.
Геометрическая интерпретация неустойчивости нулевого решения системы (2.8) в двумерном случае дана на рис. 2.7.
3. Функции Ляпунова и теоремы Ляпунова об устойчивости и неустойчивости решений дифференциальных уравнений
Рассмотрим функцию  , которая определена в фазовом пространстве переменных
, которая определена в фазовом пространстве переменных  , непрерывна и имеет непрерывные частные производные в некоторой области
, непрерывна и имеет непрерывные частные производные в некоторой области  , включающей начало координат, и удовлетворяет условию
, включающей начало координат, и удовлетворяет условию  .
.
Определение. Функция  , где
, где  , называется определенно положительной или положительно определенной в области
, называется определенно положительной или положительно определенной в области  , если
, если  для любых
для любых  ,
,  . Если
. Если  для любых
для любых  ,
,  , то функция
, то функция  называется определенно отрицательной или отрицательно определенной. В обоих случаях
называется определенно отрицательной или отрицательно определенной. В обоих случаях  называется также знакоопределенной.
называется также знакоопределенной.
Определение. Если для любых 
 или
или  , то функция
, то функция  называется знакопостоянной, причем в первом случае она знакоположительная, а во втором случае – знакоотрицательная.
называется знакопостоянной, причем в первом случае она знакоположительная, а во втором случае – знакоотрицательная.
Определение. Если в области  функция
функция  принимает как положительные, так и отрицательные значения, то в этом случае
принимает как положительные, так и отрицательные значения, то в этом случае  называется знакопеременной функцией.
называется знакопеременной функцией.
Пример 2.1.
1)  - знакопеременная в пространстве переменных
- знакопеременная в пространстве переменных  .
.
2)  - определенно положительная в пространстве переменных
- определенно положительная в пространстве переменных  .
.
3)  - знакоположительная в пространстве переменных
- знакоположительная в пространстве переменных  .
.
Очень часто в качестве функций Ляпунова для дифференциальных систем берут квадратичные формы, поэтому укажем признаки знакоопределенности квадратичных форм.
Рассмотрим квадратичную форму
, (2.9)
где
 (2.10)
(2.10)
Матрица 
коэффициентов квадратичной формы (2.9) является симметричной, то есть  , что следует из условий (2.10). Рассмотрим ее диагональные определители:
, что следует из условий (2.10). Рассмотрим ее диагональные определители:
,  . (2.11)
. (2.11)
Теорема 1. (Критерий Сильвестра). Для того, чтобы квадратичная форма (2.9), (2.10) была определенно положительной, необходимо и достаточно выполнения условий  ,
,  . Для того, чтобы квадратичная форма (2.9), (2.10) была определенно отрицательной, необходимо и достаточно выполнения условий
. Для того, чтобы квадратичная форма (2.9), (2.10) была определенно отрицательной, необходимо и достаточно выполнения условий  ,
,  .
.
Рассмотрим автономную (правые части системы не зависят от времени  ) систему дифференциальных уравнений
) систему дифференциальных уравнений
 , (2.12)
, (2.12)
где  ; ;
; ;  .
.
Предположим, что правые части системы (2.12) непрерывны и удовлетворяют условиям существования и единственности решения в некоторой области  фазового пространства. Условие
фазового пространства. Условие  означает, что точка 0 – положение равновесия системы (2.12).
означает, что точка 0 – положение равновесия системы (2.12).
Определение. Полной производной функции  в силу системы (2.12) называется производная
в силу системы (2.12) называется производная
.
Определение. Знакоопределенная в окрестности точки 0 функция  называется функцией Ляпунова для системы (2.12), если ее полная производная
называется функцией Ляпунова для системы (2.12), если ее полная производная  является знакоопределенной, знакопостоянной или тождественно равной нулю в этой окрестности.
является знакоопределенной, знакопостоянной или тождественно равной нулю в этой окрестности.
Теорема 2. (Ляпунова об устойчивости). Если для системы (2.12) существует в области  знакоопределенная функция
знакоопределенная функция  , полная производная которой по времени
, полная производная которой по времени  , вычисленная в силу системы (2.12), является знакопостоянной функцией, знак которой противоположен знаку функции
, вычисленная в силу системы (2.12), является знакопостоянной функцией, знак которой противоположен знаку функции  , или
, или  , то положения равновесия устойчиво в смысле Ляпунова.
, то положения равновесия устойчиво в смысле Ляпунова.
Теорема 3. (Ляпунова об асимптотической устойчивости). Если существует знакоопределенная функция  , полная производная которой по времени, найденная в силу системы (2.12), будет также знакоопределенной со знаком, противоположным знаку
, полная производная которой по времени, найденная в силу системы (2.12), будет также знакоопределенной со знаком, противоположным знаку  , то положение равновесия – асимптотически устойчиво.
, то положение равновесия – асимптотически устойчиво.
Теорема 4. (Первая теорема Ляпунова о неустойчивости). Если в окрестности начала координат 0 существует функция Ляпунова  такая, что ее полная производная
такая, что ее полная производная  является знакоопределенной функцией в окрестности 0 того же знака, что и
является знакоопределенной функцией в окрестности 0 того же знака, что и  , то нулевое решение системы (2.12) неустойчиво.
, то нулевое решение системы (2.12) неустойчиво.
Теорема 5. (вторая теорема Ляпунова о неустойчивости). Если существет функция  такая, что ее производная по времени имеет вид
такая, что ее производная по времени имеет вид  , где
, где  , а
, а  или тождественно равна нулю или знакопостоянна и если в последнем случае функция
или тождественно равна нулю или знакопостоянна и если в последнем случае функция  не является в любой окрестности точки 0 знакопостоянной, причем знак ее противоположен
не является в любой окрестности точки 0 знакопостоянной, причем знак ее противоположен  ,то нулевое решение системы (2.12) неустойчиво.
,то нулевое решение системы (2.12) неустойчиво.
Пример 2.2. Исследовать на устойчивость при различных значениях  нулевое решение системы:
нулевое решение системы:
(*)
Решение. Выберем функцию Ляпунова вида:  . Находим
. Находим
.
Исследуем правую часть последнего равенства.
1. Пусть  ,
,  или
или  ,
, , тогда
, тогда  . Если при этом
. Если при этом  ,
,  , то будут выполнены все условия теоремы Ляпунова об асимптотической устойчивости и нулевое решение (*) асимптотически устойчиво.
, то будут выполнены все условия теоремы Ляпунова об асимптотической устойчивости и нулевое решение (*) асимптотически устойчиво.
2. Пусть  ,
,  , . Все условия теоремы Ляпунова об устойчивости выполнены, то есть нулевое решение (*) устойчиво.
, . Все условия теоремы Ляпунова об устойчивости выполнены, то есть нулевое решение (*) устойчиво.
3. Пусть  ,
,  ,
,  или
или  ,
,  ,
,  . Тогда выполнены все условия первой теоремы Ляпунова о неустойчивости, и нулевое решение (*) неустойчиво.
. Тогда выполнены все условия первой теоремы Ляпунова о неустойчивости, и нулевое решение (*) неустойчиво.
4. Линейные однородные дифференциальные уравнения с постоянными коэффициентами и устойчивость их решений
Рассмотрим дифференциальное уравнение вида
. (2.13)
Составим характеристическое уравнение:
 . (2.14)
. (2.14)
Определим корни уравнения (2.14) и запишем фундаментальную систему решений для уравнения (2.13):  . Тогда его общее решение имеет вид:
. Тогда его общее решение имеет вид:
 . (2.15).
. (2.15).
Произвольные постоянные  определим по начальным условиям:
определим по начальным условиям:
 ,
,  ,…,
,…,  .
.
Получим частное решение:
 . (2.16)
. (2.16)
Фундаментальная система решений находится в зависимости от корней характеристического уравнения (2.14):
а) каждому действительному корню соответствует решение
 , 2.17)
, 2.17)
б) каждому действительному корню кратности m ставится в соответствие m решений:
 (2.18)
(2.18)
в) каждой паре комплексно – сопряженных корней  характеристического уравнение ставится в соответствие два решения:
характеристического уравнение ставится в соответствие два решения:
 и
и  , (2.19)
, (2.19)
г) каждой паре m – кратных комплексно – сопряженных корней  характеристического уравнения ставится в соответствие 2m решений:
характеристического уравнения ставится в соответствие 2m решений:
(2.20)
Рассмотрим поведение решений (2.17) – (2.20) при  .
.
Пусть в решениях (2.17), (2.18)  . Тогда
. Тогда
Пусть в решениях (2.19), (2.20)  . Тогда
. Тогда
, , если  .
.
Функции  ,
,  неограниченны при
неограниченны при  , если
, если  .
.
Теперь пусть в решениях (2.17), (2.18)  . Тогда
. Тогда  и решение (2.17) приводит к
и решение (2.17) приводит к  , то есть к ограниченной функции, а решение (2.18), так как
, то есть к ограниченной функции, а решение (2.18), так как  , - к неограниченным при
, - к неограниченным при  функциям.
функциям.
Определение. Корни характеристического уравнения (2.14) называются характеристическими числами уравнения (2.13).
Теорема 1. Если все характеристические числа уравнения (2.13) имеют отрицательные действительные части, то нулевое решение (2.13) асимптотически устойчиво в смысле Ляпунова (при  ).
).
Теорема 2. Если хоть одно из характеристических чисел уравнения (2.13) имеет положительную действительную часть, то нулевое решение (2.13) неустойчиво.
Теорема 3. Если среди корней характеристического уравнения (2.14) нет таких, у которых действительная часть положительна, но имеются корни с нулевой действительной частью, причем каждому такому корню соответствуют только решения вида (2.17) при  и (2.19) при
и (2.19) при  , то нулевое решение уравнения (2.13) устойчиво неасимптотически; если же хотя бы одному нулевому корню
, то нулевое решение уравнения (2.13) устойчиво неасимптотически; если же хотя бы одному нулевому корню  соответствует хотя бы одно решение вида (2.18) при
соответствует хотя бы одно решение вида (2.18) при  или хотя бы одному корню с нулевой действительной частью
или хотя бы одному корню с нулевой действительной частью  соответствует хотя бы одно решение вида (2.20) при
соответствует хотя бы одно решение вида (2.20) при  , то нулевое решение уравнения (2.13) неустойчиво.
, то нулевое решение уравнения (2.13) неустойчиво.
Пример 2.3. Исследовать на устойчивость нулевое решение уравнения  .
.
Решение. Характеристические числа данного уравнения  ,
,  . Согласно теореме 1, нулевое решение уравнения устойчиво асимптотически. Более того, оно устойчиво асимптотически в целом, так как областью притяжения нулевого решения является все фазовое пространство (
. Согласно теореме 1, нулевое решение уравнения устойчиво асимптотически. Более того, оно устойчиво асимптотически в целом, так как областью притяжения нулевого решения является все фазовое пространство ( ).
).
Пример 2.4. Исследовать на устойчивость нулевое решение уравнения  .
.
Решение. Среди характеристических чисел данного уравнения есть положительное:  . По теореме 2 нулевое решение данного уравнения неустойчиво.
. По теореме 2 нулевое решение данного уравнения неустойчиво.
Пример 2.5. Исследовать на устойчивость нулевое решение уравнения  .
.
Решение. Характеристические числа данного уравнения  ,
,  ,
,  .
.
Корню  соответствует решение
соответствует решение  , а корням
, а корням  -
-  ,
,  . Поэтому согласно теореме 3, нулевое решение данного уравнения устойчиво неасимптотически.
. Поэтому согласно теореме 3, нулевое решение данного уравнения устойчиво неасимптотически.
Пример 2.6. Исследовать на устойчивость нулевое решение уравнения  .
.
Решение. Среди характеристических чисел данного уравнения есть нулевое двукратное:  , Ему соответствует решение вида (2.20) при
, Ему соответствует решение вида (2.20) при  . Следовательно, согласно теореме 3, нулевое решение неустойчиво.
. Следовательно, согласно теореме 3, нулевое решение неустойчиво.
5. Линейные однородные системы дифференциальных уравнений с постоянными коэффициентами и устойчивость их решений
Рассмотрим систему
(2.21)
По аналогии с однородным дифференциальным уравнением с постоянными коэффициентами будем искать частное решение (2.21) в виде:
(2.22)
Подставим  и
и  в систему (2.21), сократим полученное равенство на
в систему (2.21), сократим полученное равенство на  . В результате придем к линейной алгебраической системе относительно
. В результате придем к линейной алгебраической системе относительно :
:
 (2.23)
(2.23)
Система (2.23) однородная и существует ее решение, отличное от тривиального только тогда, когда определитель этой системы  , т.е.
, т.е.
(2.24)
Уравнение (2.24) называется характеристическим уравнением системы (2.21), его корни – характеристические числа системы (2.21).
Для того, чтобы  из формулы (2.22) являлось решением уравнения (2.21), отличным от тривиального, необходимо и достаточно, чтобы
из формулы (2.22) являлось решением уравнения (2.21), отличным от тривиального, необходимо и достаточно, чтобы  было характеристическим числом системы (2.21).
было характеристическим числом системы (2.21).
Алгебраическое уравнение (2.24) имеет ровно n корней. В зависимости от вида характеристических чисел можно построить фундаментальную систему решений системы (2.21) и найти общее решение системы (2.21) как линейную комбинацию решений по аналогии с однородными линейными уравнениями.
Теорема 1. Если все характеристические числа системы (17.21) имеют отрицательные действительные части, то нулевое решение этой системы асимптотически устойчиво.
Теорема 2. Если хоть одно из характеристических чисел системы (2.21) имеет положительную действительную часть, то нулевое решение этой системы неустойчиво.
Теорема 3. Если среди характеристических чисел системы (2.21) нет таких, у которых действительная часть положительна, но имеются характеристические числа с нулевой действительной частью, то нулевое решение системы (2.21) может быть устойчивым неасимптотически или неустойчивым.
Для исследования устойчивости нулевого решения линейной системы с постоянными коэффициентами не обязательно решать характеристическое уравнение, а достаточно лишь установить, какие знаки имеют действительные части характеристических чисел.
Приведем один из критериев, который позволяет по коэффициентам системы сразу установить, когда все ее характеристические числа имеют отрицательные действительные части, и, следовательно, нулевое решение данной системы асимптотически устойчиво. Для этого запишем характеристическое уравнение (2.24) в виде (2.14):
. (2.25)
Из коэффициентов многочлена  составим матрицу:
составим матрицу:
. (2.26)
В этой матрице полагаем  , если mn. Рассмотрим диагональные определители матрицы (2.26):
, если mn. Рассмотрим диагональные определители матрицы (2.26):
Теорема 4. (Гурвица). Для того, чтобы все корни уравнения (2.25) имели отрицательные действительные части, необходимо и достаточно, чтобы выполнялись неравенства
(2.27)
Условия (2.27) называются условиями Рауса - Гурвица.
Пусть n=2, т.е.  . Тогда условие (2.27) принимает вид:
. Тогда условие (2.27) принимает вид:
Таким образом, при n=2, условия Рауса - Гурвица запишутся так:
 (2.28)
(2.28)
При n=3 имеем и условия (2.27) приобретут вид
и условия (2.27) приобретут вид
Окончательно имеем:
 (2.29)
(2.29)
условия Гуса – Гурвица в случае n=3. Аналогично находим условия Рауса – Гурвица в случаях n=4, n=5 и т.д.
Пример 2.7. Выяснить, при каких α и β (в какой области плоскости параметров α, β) устойчиво нулевое решение системы
(1)
Решение.
Характеристическое уравнение данной системы имеет вид

где
Устойчивость или неустойчивость нулевого решения системы (1) зависит от знаков  . Так как
. Так как  являются непрерывными функциями от α и β, то знаки
являются непрерывными функциями от α и β, то знаки  могут обращаться в нуль, т.е. на линиях Эти линии пересекаются в одной точке A(2,-4) и разбивает плоскость на шесть областей (рис. 2.11), в каждой из которых знаки
могут обращаться в нуль, т.е. на линиях Эти линии пересекаются в одной точке A(2,-4) и разбивает плоскость на шесть областей (рис. 2.11), в каждой из которых знаки  неизменны. Поэтому, взяв в каждой из этих областей произвольную точку, можно определить знаки коэффициентов в соответствующей области:
неизменны. Поэтому, взяв в каждой из этих областей произвольную точку, можно определить знаки коэффициентов в соответствующей области:
Характеристические числа системы (1) выражаются через  по формуле
по формуле
Если  то или
то или  (тогда одно из характеристических чисел положительно), или
(тогда одно из характеристических чисел положительно), или  (характеристические числа – комплексно- сопряженные с действительной частью). Если
(характеристические числа – комплексно- сопряженные с действительной частью). Если  то
то  и одно из характеристических чисел положительно. Следовательно, в областях II, III, IV, VI нулевое решение системы (1) неустойчиво (см. теорему 2). При
и одно из характеристических чисел положительно. Следовательно, в областях II, III, IV, VI нулевое решение системы (1) неустойчиво (см. теорему 2). При  (условия Рауса – Гурвица) имеем
(условия Рауса – Гурвица) имеем . Поэтому в областях I и V движение устойчиво асимптотически (см. теорему 1).
. Поэтому в областях I и V движение устойчиво асимптотически (см. теорему 1).
Пример 2.8. Найти область асимптотической устойчивости нулевого решения системы
Решение.
Характеристическое уравнение данной системы имеет вид
или . Корнями последнего уравнения будут . Корни
. Корни  будут отрицательными, если
будут отрицательными, если  т.е.
т.е.  . Согласно теореме 1, в области
. Согласно теореме 1, в области  нулевое решение устойчиво асимптотически. Если
нулевое решение устойчиво асимптотически. Если  то появляется один положительный корень и, согласно теореме 2, нулевое решение неустойчиво.
то появляется один положительный корень и, согласно теореме 2, нулевое решение неустойчиво.






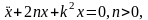
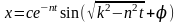
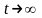 .
. 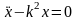 , неустойчиво, так как второе слагаемое в решении
, неустойчиво, так как второе слагаемое в решении 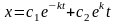 неограниченно возрастает со временем.
неограниченно возрастает со временем.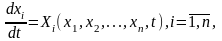 (2.1)
(2.1)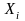 , непрерывны в некоторой области
, непрерывны в некоторой области 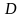 , который может совпадать со всем
, который может совпадать со всем 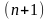 - мерным пространством переменных
- мерным пространством переменных 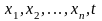 . Будем считать, что, кроме того, для системы (2.1) в области
. Будем считать, что, кроме того, для системы (2.1) в области 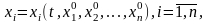 (2.2)
(2.2)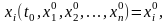 (2.3)
(2.3)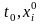 - некоторые числа из области
- некоторые числа из области 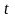 , в этом случае оно называется продолжаемым.
, в этом случае оно называется продолжаемым.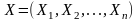 , а величину
, а величину 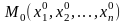
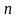 - мерного фазового пространства по траектории
- мерного фазового пространства по траектории 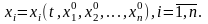
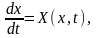 (2.4)
(2.4)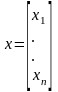 - вектор-столбец размерности
- вектор-столбец размерности  ;
;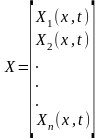 является вектором скорости.
является вектором скорости.
















