Иррациональным уравнением называется уравнение, которое содержит неизвестное под знаком корня.
Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной.
Рассмотрим два вида иррациональных уравнений, которые очень похожи на первый взгляд, но по сути сильно друг от друга отличаются.
 (1)
(1)
и
 (2)
(2)
В первом уравнении  мы видим, что неизвестное стоит под знаком корня третьей степени. Мы можем извлекать корень нечетной степени из отрицательного числа, поэтому в этом уравнении нет никаких ограничений ни на выражение, стоящее под знаком корня, ни на выражение, стоящее в правой части уравнения. Мы можем возвести обе части уравнения в третью степень, чтобы избавиться от корня. Получим равносильное уравнение:
мы видим, что неизвестное стоит под знаком корня третьей степени. Мы можем извлекать корень нечетной степени из отрицательного числа, поэтому в этом уравнении нет никаких ограничений ни на выражение, стоящее под знаком корня, ни на выражение, стоящее в правой части уравнения. Мы можем возвести обе части уравнения в третью степень, чтобы избавиться от корня. Получим равносильное уравнение:

При возведении правой и левой части уравнения в нечетную степень мы можем не опасаться получить посторонние корни.
Пример 1. Решим уравнение 
Возведем обе части уравнения в третью степень. Получим равносильное уравнение:

Перенесем все слагаемые в одну сторону и вынесем за скобки х:


Приравняем каждый множитель к нулю, получим:
 ,
,  ,
, 
Ответ: {0;1;2}
Посмотрим внимательно на второе уравнение:  . В левой части уравнения стоит квадратный корень, который принимает только неотрицательные значения. Поэтому, чтобы уравнение имело решения, правая часть тоже должна быть неотрицательной. Поэтому на правую часть уравнения накладывается условие:
. В левой части уравнения стоит квадратный корень, который принимает только неотрицательные значения. Поэтому, чтобы уравнение имело решения, правая часть тоже должна быть неотрицательной. Поэтому на правую часть уравнения накладывается условие:

 - это условие существования корней.
- это условие существования корней.
Чтобы решить уравнение такого вида, нужно обе части уравнения возвести в квадрат:
 (3)
(3)
Возведение в квадрат может привести к появлению посторонних корней, поэтому нам надо учесть ОДЗ уравнения:

 (4)
(4)
Однако, неравенство (4) следует из условия (3): если в правой части равенства стоит квадрат какого-то выражения, а квадрат любого выражения может принимать только неотрицательные значения, следовательно левая часть тоже должна быть неотрицательна. Поэтому условие (4) автоматически следует из условия (3) и наше уравнение  равносильно системе:
равносильно системе:


Пример 2. Решим уравнение:
 .
.
Перейдем к равносильной системе:


Решим первое уравнение системы и проверим, какие корни удовлетворяют неравеству.



 ,
, 
Неравеству 
 удовлетворяет только корень
удовлетворяет только корень 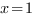
Ответ: x=1
Внимание! Если мы в процессе решения возводим обе части уравнения в квадрат, то нужно помнить, что могут появиться посторонние корни. Поэтому либо нужно переходить к равносильной системе, либо в конце решения СДЕЛАТЬ ПРОВЕРКУ: найти корни и подставить их в исходное уравнение.
Пример 3. Решим уравнение:

Чтобы решить это уравнение, нам также нужно возвести обе части в квадрат. Давайте в этом уравнении не будем заморачиваться с ОДЗ и условием существования корней, а просто в конце решения сделаем проверку.
Воозведем обе части уравнения в квадрат:

Перенесем слагаемое, содержащее корень влево, а все остальные слагаемые вправо:


Еще раз возведем обе части уравнения в квадрат:



По тереме Виета:
 ,
, 
Сделаем проверку. Для этого подставим найденные корни в исходное уравнение. Очевидно, что при  правая часть исходного уравнения отрицательна, а левая положительна.
правая часть исходного уравнения отрицательна, а левая положительна.
При  получаем верное равенство.
получаем верное равенство.
Ответ: 







 (1)
(1) (2)
(2)




 ,
,  ,
, 

 - это условие существования корней.
- это условие существования корней. (3)
(3)

 .
.



 ,
, 

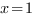







 ,
, 
 правая часть исходного уравнения отрицательна, а левая положительна.
правая часть исходного уравнения отрицательна, а левая положительна. получаем верное равенство.
получаем верное равенство.


















