Основные свойства определенных интегралов. Формула Ньютона-Лейбница для вычисления определенного интеграла. Геометрический и физический смысл определенного интеграла
Определенным интегралом от функции f(x) на отрезке [a,b] называется предел интегральной суммы (суммы Римана) при стремлении максимальной длины частичного интервала к нулю.
Свойства определенных интегралов:
Определенный интеграл от единицы равен длине интервала интегрирования:
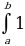 dx=b−a
dx=b−a
Постоянный множитель можно выносить за знак определенного интеграла:
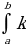 f(x)dx=k
f(x)dx=k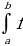 (x)dx
(x)dx
Определенный интеграл от суммы функций равен сумме интегралов от этих функций:
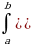 f(x)+g(x)]dx=
f(x)+g(x)]dx=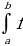 (x)dx+
(x)dx+ g(x)dx
g(x)dx
Определенный интеграл от разности функций равен разности интегралов от этих функций:
 [f(x)−g(x)]dx=
[f(x)−g(x)]dx= f(x)dx−
f(x)dx− g(x)dx
g(x)dx
Если верхний предел равен нижнему, то определенный интеграл равен нулю:
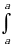 f(x)dx=0
f(x)dx=0
При перестановке пределов интегрирования определенный интеграл изменяет знак на противоположный:
 f(x)dx=−
f(x)dx=−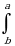 f(x)dx
f(x)dx
Пусть точка c принадлежит отрезку [a,b]. Тогда определенный интеграл от функции f(x) на отрезке [a,b] равен сумме интегралов на частичных промежутках [a,c] и [c,b]:
 f(x)dx=
f(x)dx=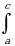 f(x)dx+
f(x)dx+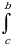 f(x)dx
f(x)dx
Определенный интеграл от неотрицательной функции всегда больше или равен нулю:
 f(x)dx≥0, если f(x)≥0 на [a,b].
f(x)dx≥0, если f(x)≥0 на [a,b].
Определенный интеграл от неположительной функции всегда меньше или равен нулю:
 f(x)dx≤0, если f(x)≤0 на [a,b].
f(x)dx≤0, если f(x)≤0 на [a,b].
Формула Ньютона-Лейбница
Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедлива формула Ньютона-Лейбница:
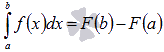 .
.
Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления.
Для доказательства формулы Ньютона-Лейбница нам потребуется понятие интеграла с переменным верхним пределом.
Если функция y = f(x) непрерывна на отрезке [a; b], то для аргумента  интеграл вида
интеграл вида 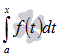 является функцией верхнего предела. Обозначим эту функцию
является функцией верхнего предела. Обозначим эту функцию 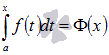 , причем эта функция непрерывная и справедливо равенство
, причем эта функция непрерывная и справедливо равенство 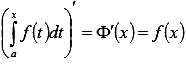 .
.
Действительно, запишем приращение функции 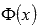 , соответствующее приращению аргумента
, соответствующее приращению аргумента 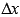 и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства:
и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства:
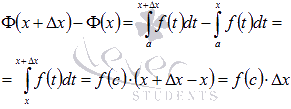
где 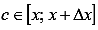 .
.
Перепишем это равенство в виде 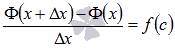 . Если вспомнить определение производной функции и перейти к пределу при
. Если вспомнить определение производной функции и перейти к пределу при  , то получим
, то получим  . То есть,
. То есть, 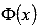 - это одна из первообразных функции y = f(x) на отрезке [a; b]. Таким образом, множество всех первообразных F(x) можно записать как
- это одна из первообразных функции y = f(x) на отрезке [a; b]. Таким образом, множество всех первообразных F(x) можно записать как  , где С – произвольная постоянная.
, где С – произвольная постоянная.
Вычислим F(a), используя первое свойство определенного интеграла: 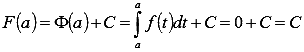 , следовательно,
, следовательно,  . Воспользуемся этим результатом при вычислении F(b):
. Воспользуемся этим результатом при вычислении F(b): 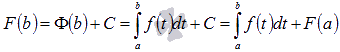 , то есть
, то есть 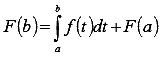 . Это равенство дает доказываемую формулу Ньютона-Лейбница
. Это равенство дает доказываемую формулу Ньютона-Лейбница 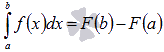 .
.
Приращение функции принято обозначать как 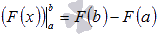 . Пользуясь этим обозначением, формула Ньютона-Лейбница примет вид
. Пользуясь этим обозначением, формула Ньютона-Лейбница примет вид 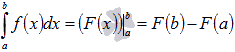 .
.
Для применения формулы Ньютона-Лейбница нам достаточно знать одну из первообразных y=F(x) подынтегральной функции y=f(x) на отрезке [a; b] и вычислить приращение этой первообразной на этом отрезке. В статье методы интегрирования разобраны основные способы нахождения первообразной. Приведем несколько примеров вычисления определенных интегралов по формуле Ньютона-Лейбница для разъяснения.
Пример. Вычислить значение определенного интеграла 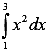 по формуле Ньютона-Лейбница.
по формуле Ньютона-Лейбница.
Решение.
Для начала отметим, что подынтегральная функция  непрерывна на отрезке [1;3], следовательно, интегрируема на нем. (Об интегрируемых функциях мы говорили в разделе функции, для которых существует определенный интеграл).
непрерывна на отрезке [1;3], следовательно, интегрируема на нем. (Об интегрируемых функциях мы говорили в разделе функции, для которых существует определенный интеграл).
Из таблицы неопределенных интегралов видно, что для функции  множество первообразных для всех действительных значений аргумента (следовательно, и для
множество первообразных для всех действительных значений аргумента (следовательно, и для 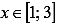 ) записывается как
) записывается как  . Возьмем первообразную при C = 0:
. Возьмем первообразную при C = 0:  .
.
Теперь осталось воспользоваться формулой Ньютона-Лейбница для вычисления определенного интеграла:  .
.
Геометрический и физический смысл определенного интеграла
Площадь криволинейной трапеции
Пусть на отрезке [а; b] задана непрерывная функция у = ƒ(х) ≥ 0. Фигура, ограниченная сверху графиком функции у = ƒ(х), снизу — осью Ох, сбоку — прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции.
Д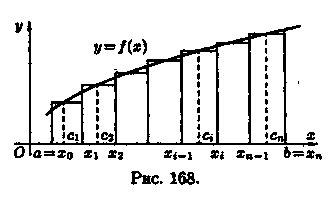 ля этого отрезок [а; b] точками а=х0, х1, ..., b=хn (х01n) paзобьем на n частичных отрезков [хо;х1], [х1;х2],...,[хn-1;хn]. (см. рис. 168). В каждом частичном отрезке [xi-1;xi] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(ci).
ля этого отрезок [а; b] точками а=х0, х1, ..., b=хn (х01n) paзобьем на n частичных отрезков [хо;х1], [х1;х2],...,[хn-1;хn]. (см. рис. 168). В каждом частичном отрезке [xi-1;xi] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(ci).
Умножим значением функции ƒ(ci) на длину ∆xi=xi-xi-1соответствующего частичного отрезка. Произведение ƒ(ci) • ∆xi равно площади прямоугольника с основанием ∆xi и высотой ƒ(ci). Сумма всех таких произведений

равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:
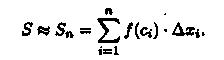
С уменьшением всех величин Δхi точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sn, когда n неограниченно возрастает так, что λ = max∆xi →0:
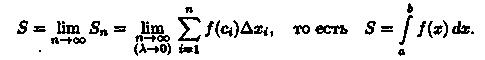
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
В этом состоит геометрический смысл определенного интеграла.
Работа переменной силы
Пусть материальная точка М перемещается под действием силы F, направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х — абсцисса движущейся точки М.
Найдем работу А силы F по перемещению точки М вдоль оси Ох из точки х = а в точку х = b (а 0, х1, ..., b = хn (х0 1 n) разобьем на n частичных отрезков [х0; x1], [x1; x2],..., [xn-1; xn]. Сила, действующая на отрезке [xi-1; xi], меняется от точки к точке. Но если длина отрезка Δхi = хi-xi-1 достаточно мала, то сила F на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F = F(x) в произвольно выбранной точке х = ci Î [xi-1; xi]. Поэтому работа, совершенная этой силой на отрезке [xi-1;xi], равна произведению F(ci)•Δхi (Как работа постоянной силы F(ci) на участке [xi-1; xi].)
Приближенное значение работы А силы F на всем отрезке [а; b] есть
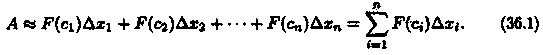
Это приближенное равенство тем точнее, чем меньше длина Δхi Поэтому за точное значение работы А принимается предел суммы (36.1) при условии, что наибольшая длина λ частичных отрезков стремится к нулю: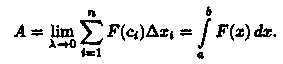 Итак, работа переменной силы F , величина которой есть непрерывная функция F = F(x), действующей на отрезке [а; b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а; b].
Итак, работа переменной силы F , величина которой есть непрерывная функция F = F(x), действующей на отрезке [а; b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а; b].
В этом состоит физический смысл определенного интеграла.
Аналогично можно показать, что путь S, пройденный точкой за промежуток времени от
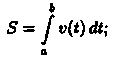
t=а до t=b, равен определенному интегралу от скорости v(t):
м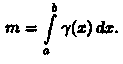 асса m неоднородного стержня на отрезке [a,b] равна определенному интегралу от
асса m неоднородного стержня на отрезке [a,b] равна определенному интегралу от
плотности g(х):
Контрольные вопросы:
Что называется определенным интегралом от функции?
Какими свойствами обладают определенные интегралы?
Как выглядит формула Ньютона-Лейбница?
В чем геометрический смысл определенного интеграла?
В чем состоит физический смысл определенного интеграла?






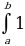 dx=b−a
dx=b−a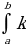 f(x)dx=k
f(x)dx=k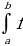 (x)dx
(x)dx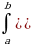 f(x)+g(x)]dx=
f(x)+g(x)]dx= g(x)dx
g(x)dx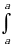 f(x)dx=0
f(x)dx=0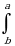 f(x)dx
f(x)dx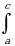 f(x)dx+
f(x)dx+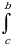 f(x)dx
f(x)dx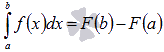 .
.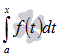 является функцией верхнего предела. Обозначим эту функцию
является функцией верхнего предела. Обозначим эту функцию 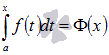 , причем эта функция непрерывная и справедливо равенство
, причем эта функция непрерывная и справедливо равенство 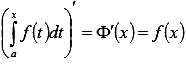 .
.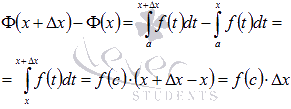
 , где С – произвольная постоянная.
, где С – произвольная постоянная.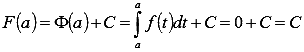 , следовательно,
, следовательно, 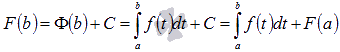 , то есть
, то есть 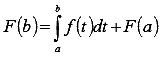 . Это равенство дает доказываемую формулу Ньютона-Лейбница
. Это равенство дает доказываемую формулу Ньютона-Лейбница 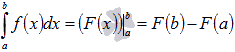 .
. . Возьмем первообразную при C = 0:
. Возьмем первообразную при C = 0:  .
. ля этого отрезок [а; b] точками а=х0, х1, ..., b=хn (х01n) paзобьем на n частичных отрезков [хо;х1], [х1;х2],...,[хn-1;хn]. (см. рис. 168). В каждом частичном отрезке [xi-1;xi] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(ci).
ля этого отрезок [а; b] точками а=х0, х1, ..., b=хn (х01n) paзобьем на n частичных отрезков [хо;х1], [х1;х2],...,[хn-1;хn]. (см. рис. 168). В каждом частичном отрезке [xi-1;xi] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(ci).
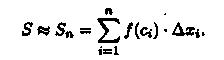
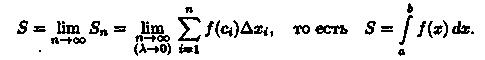
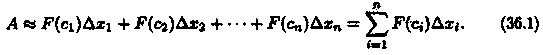
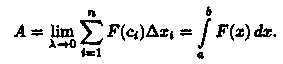 Итак, работа переменной силы F , величина которой есть непрерывная функция F = F(x), действующей на отрезке [а; b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а; b].
Итак, работа переменной силы F , величина которой есть непрерывная функция F = F(x), действующей на отрезке [а; b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а; b].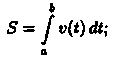
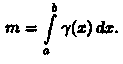 асса m неоднородного стержня на отрезке [a,b] равна определенному интегралу от
асса m неоднородного стержня на отрезке [a,b] равна определенному интегралу от 

















