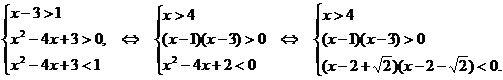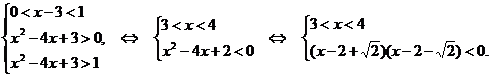Логарифмические неравенства
Неравенства вида logaxb (logax³b) или logaxb (logax£b), где a0, a¹1, называются простейшими логарифмическими неравенствами.
Решение логарифмических неравенств основано на строгой монотонности логарифмической функции. Известно, что
o при основании, большем единицы, логарифмическая функция возрастает,
o при положительном основании, меньшем единицы, логарифмическая функция убывает.
Неравенство вида
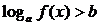
эквивалентно следующим системам неравенств1[1]
o при a1 f(x)0, f(x)ab;
o при 00, f(x)b.
Неравенство вида
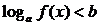
эквивалентно следующим системам неравенств
o при a1 f(x)0, f(x)ab;
o при 00, f(x)ab.
Пример 1 Решить неравенство log8(x2-4x+3).
Решение. Так как основание логарифма больше единицы (а=8), то данное неравенство эквивалентно системе:
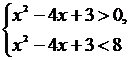 или
или 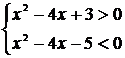 .
.
Каждое неравенство решим методом интервалов.
х2-4x+3=0 при х1=1, х2=3. Определяя знаки, получим:
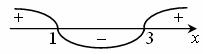
х2-4x-5=0 при х1=-1, х2=5. Определяя знаки, получим
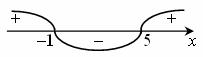
Совмещая промежутки, имеем:
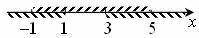
Таким образом, 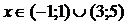 .
.
Ответ: 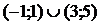 .
.
Неравенство вида
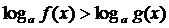
эквивалентно следующим системам неравенств:
o при a1 f(x)0, g(x)0, f(x)g(x);
o при 00, g(x)0, f(x).
Неравенство вида
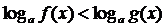
эквивалентно следующим системам неравенств
o при a1 f(x)0, g(x)0, f(x)g(x);
o при 00, g(x)0, f(x)g(x).
Пример2. Решить неравенство:
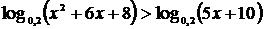 .
.
Решение. Основание логарифмической функции меньше 1 (a=0,2). Поэтому, выписывая области определения выражений левой и правой частей неравенства и пользуясь свойством монотонности, получим равносильную систему:
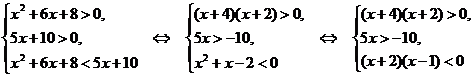 .
.
Решение неравенств второй степени методом интервалов:
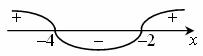
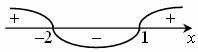
Совмещая промежутки, получим:
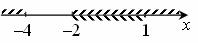
Ответ: (-2;1).
Более сложные логарифмические неравенства сводятся к простейшим методами, аналогичными используемым при решении логарифмических уравнений.
Пример 3. Решить неравенство:
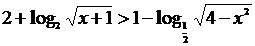 .
.
Решение. Переходя к основанию 2 в выражении, стоящем в правой части данного неравенства, получим:
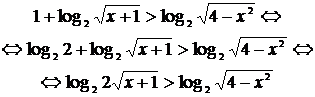
Теперь перейдем к равносильной системе:
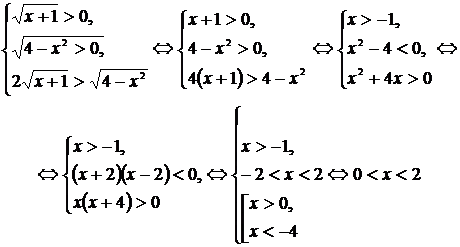
Решение встречающихся квадратичных неравенств провели методом интервалов:

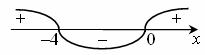
Совмещая промежутки, получим 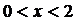 .
.
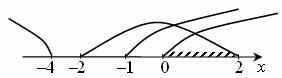
Ответ: (0; 2).
Пример 4. Решить неравенство  .
.
Решение. Так как выражения, стоящие в левой и правой частях неравенства положительны, то для решения прологарифмируем обе части по основанию 10. Получим равносильное исходному неравенство:
 ,
,
или, пользуясь свойствами логарифмов
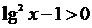 .
.
Обозначая t=lg x, решим неравенство t2-10:

то есть t или t1.
Решая неравенства lg x, а также lg x1, имеем соответственно:
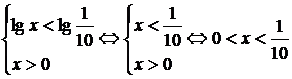 .
.
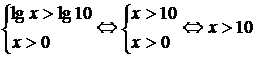 .
.
Ответ: (0; 0,1)È(10;+¥).
Если в неравенстве встречается логарифмическая функция, содержащая неизвестное в основании, то, как правило, следует рассматривать два случая:
o когда основание больше 1
o когда основание положительно, но меньше 1.
Неравенство с переменным основанием можно также решать, используя формулы перехода к новому, не содержащему неизвестное, основанию.
Пример 5. Решить неравенство logx-3(x2-4x+3).
Решение. Так как основание логарифма содержит переменную, то рассмотрим два случая x-31 и 0x-3.
Если основание логарифма больше одного, то пользуясь свойством монотонности с учетом ОДЗ, получим:
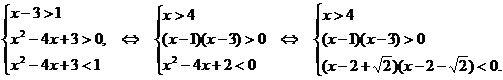
Решая неравенства методом интервалов, получим:
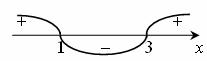
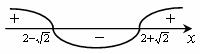
Совмещаем промежутки и убеждаемся, что данная система не имеет решений.
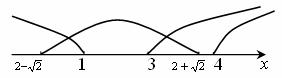
Рассмотрим второй случай, если 0. В этом случае получаем систему:
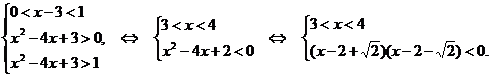
Совмещая промежутки, получаем:
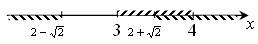
Ответ: 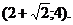

1[1] В случае, если неравенство нестрогое, вторые неравенства этих систем также нестрогие.





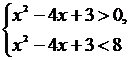 или
или 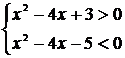 .
.

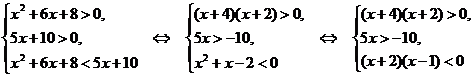 .
.

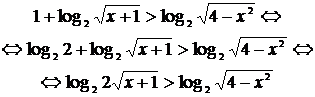
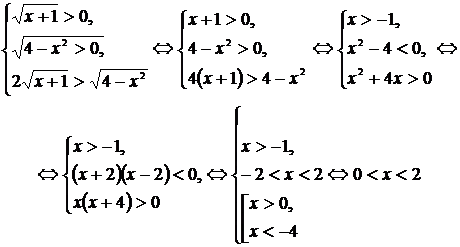




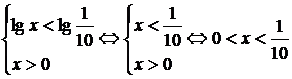 .
.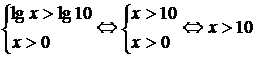 .
.