Лекция №3.
Понятие вероятности.
Классическое определение вероятности.
Определение: Вероятностью события А называется число, равное отношению числа m – благоприятствующих исходов событию А, к числу n – всех возможных исходов, обозначают:
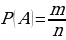
Пример 1.
Найти вероятность выпадения четного числа очков при бросании игральной кости.
Решение.
Множество всех элементарных исходов данного испытания состоит из шести
элементов n = 6. Благоприятствующими событию А = {выпало четное число очков} будут элементарные события – выпадение 2, 4 и 6 очков, т.е. m = 3.
Вероятность события 
Свойства вероятности.
1. Для любого случайного события выполняется 0 ≤ P(А) ≤ 1.
2. Вероятность достоверного события равна единице P(Ω) = 1.
3. Вероятность невозможного события равна нулю 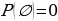 .
.
4. Теорема сложения вероятностей.
Вероятность суммы несовместных событий равна сумме вероятностей этих событий:
P(A+B) = P(A) + P(B). В случае n несовместных событий справедливо:
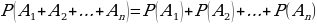
5. Вероятность противоположного события равна  , т.к. сумма вероятностей противоположных событий А и
, т.к. сумма вероятностей противоположных событий А и 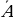 равна единице:
равна единице:  .
.
6. Теорема умножения вероятностей.
Вероятность произведения независимых событий равна произведению вероятностей этих событий: P(A∙B) = P(A) ∙ P(B). В случае n независимых событий справедливо:
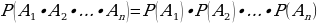
7. Если события совместные, то P(A+B) = P(A) + P(B) – P(A∙B).
Пример 2.
Два стрелка стреляют по мишени. Вероятность попадания для первого стрелка – 0,7, для второго – 0,8.
Найти вероятности следующих событий:
а) оба стрелка попадут в цель;
б) оба стрелка промахнутся;
в) только один стрелок попадёт в цель;
г) хотя бы один попадёт.
Решение.
Рассмотрим следующие события:
A – «попал первый стрелок»,
B – «попал второй стрелок»,
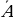 – «первый не попал»,
– «первый не попал»,
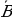 – «второй не попал».
– «второй не попал».
Тогда, по условию задачи вероятности этих событий равны:
Р(А) = 0,7;  = 1 – 0,7 = 0,3;
= 1 – 0,7 = 0,3;
Р(В) = 0,8; 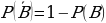 = 1 – 0,8 = 0,2.
= 1 – 0,8 = 0,2.
Используя операции над событиями, найдем искомые вероятности:
а) оба стрелка попадут в цель
Р(А∙В) = Р(А)∙Р(В) = 0,7∙0,8 = 0,56.
б) оба стрелка промахнутся
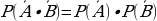 = 0,3∙0,2 = 0,06.
= 0,3∙0,2 = 0,06.
в) только один стрелок попадёт в цель
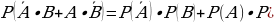 ) = 0,3∙0,8+0,7∙0,2 = 0,38.
) = 0,3∙0,8+0,7∙0,2 = 0,38.
г) хотя бы один попадёт:
Событие 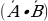 («оба стрелка промахнулись») будет противоположным для события «хотя бы один попал в цель». Следовательно, искомая вероятность находится так:
(«оба стрелка промахнулись») будет противоположным для события «хотя бы один попал в цель». Следовательно, искомая вероятность находится так:
1 – Р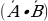 = 1 – 0,2∙0,3 = 0,94.
= 1 – 0,2∙0,3 = 0,94.
Условная вероятность. Формула полной вероятности.
Формулы Байеса.
Определение: Условной вероятностью события В при условии, что событие А произошло называется вероятность 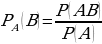 . Обзначается:
. Обзначается:  или Р(В/А).
или Р(В/А).
Теорема умножения (для зависимых событий). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого:

В случае произвольного числа событий теорема умножения имеет вид:
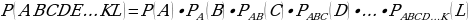
Пример 3.
Студент выучил 15 из 40 экзаменационных вопросов. Найти вероятность того, что в наудачу взятом билете он знает оба вопроса.
Решение.
Рассмотрим события А={первый вопрос в билете студент знает}, В={второй вопрос в билете студент знает}.
Очевидно, что вероятность Р(А) = 15/40.
Вероятность события В найдем из условия, что всех исходов осталось 39 и благоприятствующих 14, тогда РА(В) = 14/39.
Итак, искомая вероятность, что в наудачу взятом билете он знает оба вопроса, будет равна:

События Н1, Н2, Н3, …, Нn образуют полную группу событий, если выполняются следующие
условия:
1) 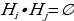 – события попарно несовместны;
– события попарно несовместны;
2) 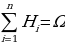 – их сумма равна достоверному событию.
– их сумма равна достоверному событию.
Очевидно, что  .
.
Пусть требуется найти вероятность события А, которое может произойти после того, как произойдет одно из событий Н1, Н2, Н3, …, Нn, образующих полную группу событий. Искомая вероятность находится по следующей формуле, которая называется формулой полной вероятности:
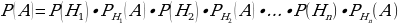
или:
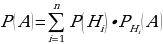
Пример 4.
С первого станка-автомата поступают 30% деталей, со второго – 25%, с третьего – 45%. Бракованных деталей поступает с первого станка 2%, со второго – 1%, с третьего – 3%. Какова вероятность того, что выбранная наудачу деталь бракованная?
Решение.
Обозначим через А интересующее нас событие: А={выбранная наудачу деталь бракованная}. Поскольку выбранная деталь могла быть изготовлена на любом из трех станков-автоматов, введем события
Hi = {деталь изготовлена на i-ойм станке}, i=1,2,3.
Из условия задачи следует, что Р(Н1) = 0,30; Р(Н2) = 0,25; Р(Н3) = 0,45.
События H1, H2, H3 попарно несовместны, сумма их вероятностей равна единице, следовательно, они образуют полную группу событий и можно воспользоваться формулой полной вероятности:
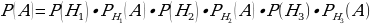
Из условия задачи 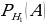 означает вероятность того, что наудачу выбранная деталь окажется бракованной и изготовленной на первом станке, она равна
означает вероятность того, что наудачу выбранная деталь окажется бракованной и изготовленной на первом станке, она равна 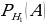 = 0,02.
= 0,02.
Аналогично: 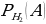 = 0,01;
= 0,01;  = 0,03.
= 0,03.
По формуле полной вероятности найдем требуемую вероятность события А:
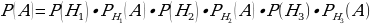 = 0,3∙0,02 + 0,25∙0,01 + 0,45∙0,01 = 0,022.
= 0,3∙0,02 + 0,25∙0,01 + 0,45∙0,01 = 0,022.






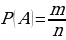

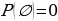 .
.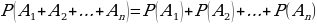
 , т.к. сумма вероятностей противоположных событий А и
, т.к. сумма вероятностей противоположных событий А и 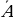 равна единице:
равна единице:  .
.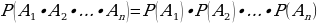
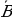 – «второй не попал».
– «второй не попал».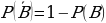 = 1 – 0,8 = 0,2.
= 1 – 0,8 = 0,2.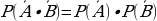 = 0,3∙0,2 = 0,06.
= 0,3∙0,2 = 0,06.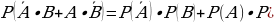 ) = 0,3∙0,8+0,7∙0,2 = 0,38.
) = 0,3∙0,8+0,7∙0,2 = 0,38.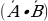 («оба стрелка промахнулись») будет противоположным для события «хотя бы один попал в цель». Следовательно, искомая вероятность находится так:
(«оба стрелка промахнулись») будет противоположным для события «хотя бы один попал в цель». Следовательно, искомая вероятность находится так: 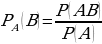 . Обзначается:
. Обзначается:  или Р(В/А).
или Р(В/А).
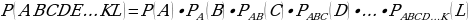

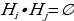 – события попарно несовместны;
– события попарно несовместны;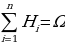 – их сумма равна достоверному событию.
– их сумма равна достоверному событию. .
.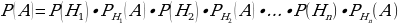
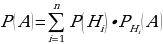
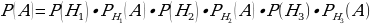
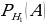 означает вероятность того, что наудачу выбранная деталь окажется бракованной и изготовленной на первом станке, она равна
означает вероятность того, что наудачу выбранная деталь окажется бракованной и изготовленной на первом станке, она равна 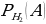 = 0,01;
= 0,01;  = 0,03.
= 0,03.
















