Характеристики случайных величин. Математическое ожидание. Дисперсия и стандартное отклонение. Условная вероятность. Неравенство Чебышева

"Методика достижения и оценки образовательных результатов по теме "Характеристики случайных величин. Математическое ожидание. Дисперсия и стандартное отклонение. Условная вероятность. Неравенство Чебышева"

• Математическая статистика – это раздел математики, посвященный методам сбора, анализа и обработки результатов статистических данных наблюдений для научных и практических целей.

• Одной из центральных задач математической статистики является задача оценивания теоретического распределения случайной величины на основе выборочных данных. При этом часто предполагается, что вид закона распределения генеральной совокупности известен, но неизвестны параметры этого закона, такие, например, как математическое ожидание, дисперсия. Требуется найти приближенные значения этих параметров, т.е. получить статистические оценки указанных параметров.

Математическое ожидание

Задача № 509373

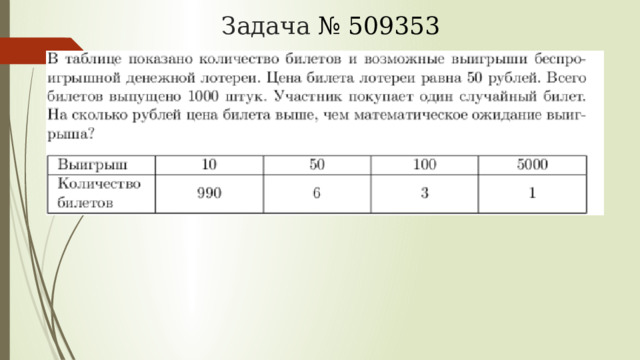
Задача № 509353

Примечание.

Понятие матожидания является относительно новым для российской школы, поэтому сделаем небольшое замечание. Матожидание выигрыша это характеристика, показывающая сколько в среднем получит или потеряет игрок, если при неизменных условиях будет играть достаточно долго. Полученный выше результат говорит о том, что каждый раз выигрывая (лотерея  — беспроигрышная) купивший билет, тем не менее, в среднем будет терять 34,5 рубля за игру.

Дисперсия и стандартное отклонение

• В статистике оценка дисперсии является важным понятием, которое позволяет измерить разброс данных вокруг их среднего значения. Однако, чтобы получить точную оценку дисперсии, необходимо использовать несмещенную оценку. 
• Оценка дисперсии – это статистическая мера, которая позволяет оценить разброс значений вокруг среднего значения выборки. Дисперсия является одной из основных характеристик распределения данных и позволяет понять, насколько значения выборки отклоняются от среднего значения.
• Дисперсия обычно обозначается как σ² (сигма в квадрате) и вычисляется путем нахождения среднего квадратичного отклонения от среднего значения выборки. Однако, чтобы получить точную оценку дисперсии для всей генеральной совокупности, нам нужно знать все значения в генеральной совокупности, что часто невозможно. Поэтому мы используем оценку дисперсии на основе выборки.
• Оценка дисперсии на основе выборки позволяет нам приближенно оценить дисперсию генеральной совокупности, используя только данные из выборки. Она является статистической оценкой и может быть смещенной или несмещенной.

Несмещенная оценка

• Несмещенная оценка – это оценка параметра, которая в среднем равна истинному значению параметра. В контексте оценки дисперсии, несмещенная оценка дисперсии означает, что среднее значение оценки дисперсии равно истинной дисперсии генеральной совокупности.
• Формально, пусть X1, X2, …, Xn – случайная выборка из генеральной совокупности. Оценка дисперсии S^2 называется несмещенной, если E(S^2) = σ^2, где E(S^2) – математическое ожидание оценки дисперсии, а σ^2 – истинная дисперсия генеральной совокупности.
• Несмещенная оценка дисперсии является важным свойством, так как она позволяет нам получить более точную оценку дисперсии генеральной совокупности на основе выборки. Она учитывает случайность выборки и позволяет учесть различия между выборкой и генеральной совокупностью.

Формула для несмещенной оценки дисперсии

• Формула для несмещенной оценки дисперсии основана на выборочных данный и позволяет нам оценить дисперсию генеральной совокупности на основе выборки. Формула выглядит следующим образом:
• S^2 = (1 / (n – 1)) * Σ(xi – x̄)^2

где:

• S^2 – несмещенная оценка дисперсии
• n – размер выборки
• Σ – сумма
• xi – значение i-го элемента выборки
• x̄ – среднее значение выборки

• Формула позволяет нам вычислить несмещенную оценку дисперсии, учитывая различия между выборкой и генеральной совокупностью. Здесь мы вычитаем среднее значение выборки из каждого элемента выборки, возводим результат в квадрат и суммируем все значения. Затем делим полученную сумму на (n – 1), где n – размер выборки, чтобы получить несмещенную оценку дисперсии.

Свойства несмещенной оценки дисперсии

• Близость к истинному значению

Несмещенная оценка дисперсии стремится к истинному значению дисперсии при увеличении размера выборки. Это означает, что с увеличением количества наблюдений оценка становится все более точной и приближается к истинному значению дисперсии.

• Сохранение свойств дисперсии

Несмещенная оценка дисперсии сохраняет основные свойства дисперсии. Например, если исходная случайная величина умножается на константу, то несмещенная оценка дисперсии также будет умножена на эту константу в квадрате.

• Использование в статистических тестах

Несмещенная оценка дисперсии широко используется в статистических тестах и анализе данных. Она позволяет оценить разброс значений в выборке и сравнивать различные группы или условия на основе их дисперсии.

• Сравнение различных выборок

Несмещенная оценка дисперсии позволяет сравнивать различные выборки и оценивать, насколько они отличаются друг от друга. Сравнение дисперсий может помочь выявить статистически значимые различия между группами или условиями.

• Важно помнить, что несмещенная оценка дисперсии является только оценкой и может отличаться от истинного значения дисперсии. Однако, при правильном использовании и достаточном размере выборки, она обычно дает достаточно точные результаты.

Задача № 509479

• Шаг 1: Вычисляем среднее значение выборки:
• Х=(1,4+1,2+1,3+1,4+1,2):5=6,5:5=1,3
• Шаг 2: Вычисляем разницу между каждым значением выборки и средним значением:

1,4-1,3=0,1

1,2-1,3=-0,1

1,3-1,3=0

1,4-1,3=0,1

1,2-1,3=-0,1

• Шаг 3: Возводим каждую разницу в квадрат:

=0,01

=0,01

=0

=0,01

=0,01

• Шаг 4: Суммируем все полученные значения:

0,01+0,01+0+0,01+0,01=0,04

• Шаг 5: Делим полученную сумму на (n – 1), где n – размер выборки:

0,04:(5-1)=0,04:4=0,01

• Ответ:0,01

Задача № 509480

• Ответ:2,25

Условная вероятность. Формула Байеса

• Условная вероятность — вероятность наступления события А при условии, что событие В произошло.
• Вероятность события А, вычисленная в предположении, что событие В уже произошло, обозначается
• круги Эйлера :

• Пусть для некоторого эксперимента красный круг обозначает множество всех возможных исходов. Зеленый круг обозначает множество исходов, благоприятствующих событию А, синий круг обозначает множество исходов, благоприятствующих событию В, область, лежащая в пересечении этих кругов обозначает множество исходов, благоприятствующих обоим событиям А и В, обозначим его АВ.

Вероятность события  А   в предположении, что событие В уже

произошло вычисляется по формуле

Вероятность события  В   в предположении, что событие А уже

произошло вычисляется по формуле

Задача № 509332

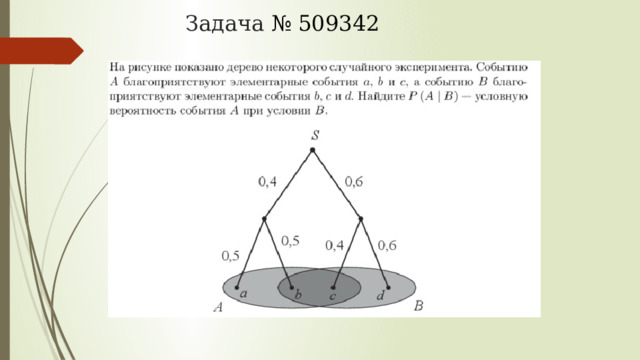
Задача № 509342

Неравенство Чебышева

Неравенство Чебышева

Когда известны не только математическое ожидание, но и дисперсия для случайной величины, можно применять следствие неравенства Маркова — неравенство Чебышева , которое дает оценку вида:

Также его можно записать в другой форме:

Неравенство Чебышева показывает, что случайная величина принимает значения близкие к среднему (математическому ожиданию) и дает оценку вероятности больших отклонений.

Задача № 509452