Муниципальное автономное образовательное учреждение
Средняя общеобразовательная школа №3 имени Героя России Сергея Ромашина
Исследовательская работа по математике
«Линейные диофантовы уравнения»
Выполнили :ученицы 8 Д класса Мачкалян Ангелина,
Авасбекова Айгерим
Научный руководитель :Цой Ю.Е.
Южно-Сахалинск
2018
Оглавление
Введение 4
Что такое линейное диофантово уравнения? 5
Диофантовы уравнения в олимпиадных задачах 6
Диофантовы уравнения в экономике 7
Применение в истории 10
Диафантовы уравнения в КИМах ЕГЭ 10
Заключение 12
Литература 13
Введение
Проблема :диофантовы уравнения не изучается в школьной программе,но для решения олимпиадных задач,а также задания уровня С ЕГЭ поэтому необходимо изучить данную тему
Актуальность
Диофантовы уравнения не изучаются в школьном курсе математики, но присутствуют во многих олимпиадных заданиях и в ЕГЭ группы С 6( № 19). Помимо этого они применяются в молекулярной физике и органической химии, системах цифровой подписи и шифрования, в экономике и теории вероятностей.
Цель- узнать что такое линейные диофатовы уравнения, как они решаются, сферы их применения.
Гипотеза исследования
Умение решать диофантовы уравнения поможет решать олимпиадные задания, а также подготовиться к решению ряду задач № 19 ЕГЭ.
Задачи исследования:
Изучить литературу, интернет-ресурсы
Узнать, как решаются, когда не имеют решений
Разобрать решение различных задач, в том числе задания №19 ЕГЭ .
Разработать сборник и предложить для решения на дополнительных занятиях по математике.
Что такое линейное диофантово уравнения?
Древнегреческий математик Диофант Александрийский занимался решением отдельных задач, равносильных неопределенным уравнениям (уравнения, содержащие несколько неизвестных), применяя для этого хитроумные, но частные методы. Между тем простой разбор задач Диофанта показывает, что он не только обозначил проблему решения неопределенных уравнений в рациональных числах, но и дал некоторые общие методы их решения.
Диофантовы уравнения – алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неизвестных в уравнениях больше числа уравнений.
Рассмотрим простое диофантово уравнение
5х-8у=19
Найдем частное решение методом подбора х=7, у=2.
1)5 х - 8 у=19;
2)57-82=19;
_______________
Вычтем из уравнения 1) второе равенство, получим
5(х-7)-8(у-2)=0
5(х-7)=8(у-2)
5 и 8 взаимно простые(НОД=1), 5 не делится на 8, следовательно делится (х-7)
x-7=8k, k-целое.
x=8k+7, подставим
5(8k+7-7)=8(y-2)
58k=8(y-2)
5k=y-2;
y=5k+2.
Ответ:(8k+7;5k+2)
Существует более удобный способ подбора частного решения.
Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент. 5х - 8у = 19 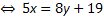
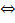 х =
х = 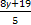 .
.
Остатки при делении на 5: 0,1,2,3,4. Подставим вместо у эти числа.
Если у = 0, то х = 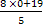 =
=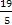 .
.
Если у =1, то х = 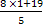 =
=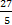 .
.
Если у = 2, то х = 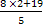 =
=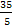 = 7
= 7 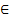 Z.
Z.
Если у =3, то х = 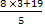 =
=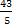 .
.
Если у = 4 то х = 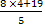 =
=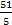 .
.
Итак, частным решением является пара (7;2).
Тогда общее решение: 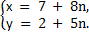 n
n 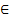 Z.
Z.
Диофантовы уравнения могут и не могут иметь решение.
Пример: 35х+28y=25
7(5x+4y)=25
7(5x+4y) делится на 7, а 25 не делится на 7, т.к. эти части равны, такого быть не может, получили противоречие, значит это уравнение не имеет решений. Мы рассмотрели множество таких уравнений и пришли к выводу, что уравнение вида
ax+by=c, не имеют решение, если a и b делятся на целое число d, а с не делится на d, то диофантовое уравнение не имеет решений.
Диофантовы уравнения в олимпиадных задачах
Диофантовы уравнения в экономике
Задача 1. Как, имея монеты в 5 копеек и в 3 копейки, заплатить кассиру в магазине 13 копеек?
Решение : х- количество монет по 5 коп., у- количество монет по 3 коп. Составим и решим уравнение 5х + 3у= 13. Подберём частное решение х=2, у=1, тогда 5·2+3·1=13,
5х + 3у = 5·2+3·1, перенесём все слагаемые в левую часть и сгруппируем
5·(х-2) + 3·(у-1) =0, обозначим х-2 = х1, у-1 = у1, тогда уравнение становиться однородным, 5х1+3у1=0, отсюда 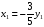 , у1 кратно 5, т.е. у1 =5n, х1 = -3n, где n- любое целое число, вернёмся к старым неизвестным х-2= -3n , х= 2-3n,
, у1 кратно 5, т.е. у1 =5n, х1 = -3n, где n- любое целое число, вернёмся к старым неизвестным х-2= -3n , х= 2-3n,
у-1= 5n, у =1+ 5n .
Ответ: х= 2-3n, у =1+ 5n , где n- любое целое число.
Замечание: Если х будет отрицательным, это значит сдача, т.е. продавец должна будет вернуть .
Задача. 2. Для перевозки зерна имеются мешки, в которые входит либо 60 кг, либо 80 кг зерна. Сколько надо заготовить тех и других мешков для загрузки 1 т зерна таким образом, чтобы все мешки были полными? Какое наименьшее количество мешков при этом может понадобиться?
Решение: Для неизвестных х и у , обозначающих количество мешков по 60 и по 80 кг соответственно, имеем уравнение 60х+80у=1000, сократив обе части уравнения получим 3 х+5 у =50. Надо решить это уравнение в целых неотрицательных числах. Одно целочисленное решение этого уравнения
(-50;50), действительно 3·(-50)+4·50 = 50.
3 х+5 у = 3·(-50)+4·50 , 3( х+50)+5( у-50)=0,
х=4n-50, у=50-3n, где n- любое целое число.
Так как число мешков неотрицательно, то 4n-50 ≥0 и 50-3n ≥0, значит
| Значение n | Значение х | Значение у | х+у |
| 13 | 2 | 11 | 13наименьшее |
| 14 | 6 | 8 | 14 |
| 15 | 10 | 5 | 15 |
| 16 | 14 | 2 | 16 |
Ответ : 13 мешков, 2 мешка по 60 кг, 11 мешков по 80 кг
Задача 3. Требуется разлить 20,5 литра сока в банки по 0,7л и 0,9 л, так, чтобы все банки оказались полными. Сколько каких банок надо заготовить? Какое наименьшее количество банок при этом может понадобиться?
Решение: Задача сводится к решению уравнения
0,7х+09у= 20,5 в целых неотрицательных числах , где х и у – количество банок по 0,7л и 0,9л соответственно.
Преобразуем уравнение к виду 7 х+9 у = 205 , а затем, делая последовательные замены переменных в левой части, получим равенства
7 х+9 у =7(х+ у)+2у= 7u+2у= u+2(у+3u) =u+2v= 205, где х+у=u, у+3u = v.
Из этих равенств имеем
u = 205-2v, у = v - 3u = v- 3(205-2v)=7v- 615 ≥ 0, х =u-у = 205-2v- (7v-615)= 820-9v ≥0.
| v | х | у | х+у |
| 88 | 28 | 1 | 29 |
| 89 | 19 | 8 | 27 |
| 90 | 10 | 15 | 25 |
| 91 | 1 | 22 | 23- наименьшая |
Ответ: 23 банки, из них 1 по 0,7л и 22 банки по 0,9 л.
Задача 4. На складе имеются гвозди, упакованные в ящики по16кг,17кг и 40кг. Может ли кладовщик отпустить 140 кг гвоздей, не вскрывая ни одного ящика
Решение:
Пусть х – количество ящиков по 16 кг,
у – количество ящиков по 17 кг,
z – количество ящиков по 40 кг
Задача сводится к решению уравнения 16х +17у+40z = 140
х=2, у = 4, z =1.
Ответ: Можно, 2 ящика по 16 кг, 4 ящика по 17 кг и 1 ящик с 40 кг.
Задача 5. ( старинная )
Двенадцать человек несут 12 хлебов; каждый мужчина несёт по 2 хлеба, женщина – по половине хлеба, ребёнок – по четверти хлеба. Сколько было мужчин, женщин и детей?
Решение: Пусть было х мужчин, у женщин, тогда детей было 12- х – у. Вместе они несли  хлебов. Составим уравнение
хлебов. Составим уравнение
 .
.
Умножим правую и левую части этого уравнения на 4 , после преобразований получим равносильное ему уравнение
7х+у = 36,
имеющий частное решение х=5, у=1 и общее решение х = 5- n,
у = 1+7n, где n- любое целое число.
Чтобы х и у и (12-х-у) были натуральными числами, можно взять только одно значение n , равное 0. При этом х = 5, у = 1, 12 – х –у = 6, т.е. было 5 мужчин,1 женщина, 6 детей.
Ответ: было 5 мужчин,1 женщина, 6 детей.
адача 1.
Андрей работает летом в кафе. За каждый час ему платят 10
руб . И высчитывают 2 р
уб . за каждую разбитую тарелку. На прошедшей
неделе он заработал 180 р
уб . Определите, сколько часов он работал и
сколько разбил тарелок, если известно, что он работает не более 3 ч в день.
Решение.
Пусть
x
часов он всего работал в неделю, тогда
10х
руб . ему заплатили,
но он разбил
у
тарелок, и с него вычли
2у
руб . Имеем уравнение
10х – 2у
=180
, причем
x
меньше или р
авен 21. Получим:
5х-у=90, 5х=90+у, х=18+у:5.
Так как
x
целое число, то
у
должно нацело делится на 5, чтобы в правой
части получилось целое число. Возможны четыре случаи:
1)
у=0, х=18, т. е. решением является пара
– (18, 0);
2)
у=5, х=19, (19, 5);
3)
у=10, х=20
, (20, 10);
4)
у=15, х=21, (21, 15).
Задача No2
. Из двухрублевых и пятирублевых монет составлена сумма в
23 рубля. Сколько среди этих монет двухрублевых?
Решение.
Пусть
x
– количество двухрублевых монет,
у –
количество пятирублевых
монет. Составим и решим ура
внение:
2х+5у=23; 2х=23
–
5у;
x = (23
– 5у):2;
x =(22+1
– 5у):2, почленно поделим 22 на 2 и (1
– 5у) на 2,
получим:
x = 11 + (1
– 5у):2.
Так как
x
и
y
натуральные числа по условию задачи, то левая час
ть
уравнения есть натуральное число, значит, и правая часть должна быть
натуральным числом. К тому же, чтобы получить в правой части число
натуральное, нужно чтобы выражение (1
– 5у) нацело делилось на 2.
Осуществим перебор вариантов.
1)
y=1, х=9, то есть дв
ухрублевых монет может быть 9;
2)
у=2, при этом выражение (1
– 5у) не делится нацело на 2;
3)
у=3, х=4, то есть двухрублевых монет может быть 4;
4)
при у больше или равном 4 значение
x не является числом
натуральным.
Таким образом, ответ в задаче следующий:
среди м
онет 9 или 4
двухрублевых.
Учащиес
Применение в истории
Стоит упомянуть одно интересное историческое приложение, использующее свойства диофантовых уравнений. Согласно некоторым источникам, китайские военачальники, чтобы узнать численность своей армии, давали несколько последовательных команд «В колонну по 7 становись!», «В колонну по 11 становись!», «В колонну по 13 становись!», «В колонну по 17 становись!» и в каждом случае выясняли, сколько солдат получилось в последнем ряду. После этого (только по полученным остаткам!) вычислялось общее количество солдат.
Диафантовы уравнения в КИМах ЕГЭ
Вариант № 144 А.Ларин , задание № 19

Из книги Ю. В,. Садовничего «Решение задач и уравнений в целых числах. Задание № 19 профильный уровень»:
Дмитрий Гущин предлагает такие задачи на своем сайте «Решу ЕГЭ»:
Заключение
В разных учебниках встречаются многие старинные задачи, которые можно решить с помощью уравнений Диофанта, в т.ч. некоторые прототипы задания № 19 профильного ЕГЭ.. Выполнив данный проект, мы научились находить целые решения линейных уравнений с двумя неизвестными , поняли, что существуют жизненные ситуации, когда необходимо решить уравнение с несколькими неизвестными в целых числах, помимо этого увидели, что спектр применения данных уравнений очень широк. В дальнейшем нам бы хотелось расширить наше исследование и рассмотреть решение диофантовых уравнений более высокого порядка, в том числе великую теорему Ферма.
Литература
Башмакова И.Г. Диофант и диофантовы уравнения. – М.: «Наука», 1972 г. - 68 с.
Гельфонд А.О. Решение уравнений в целых числах. Популярные лекции по математике, вып. М.: «Гостехиздат», 1957 г. - 66 с.
Кордемский Б.А. Увлечь школьников математикой. – М.: «Просвещение»,1981г.-141с.
Матисеевич Ю.В. Десятая проблема Гильберта. - М.: «Физматлит», 1973 г. - 224 с.
Михелович Ш.Х. Теория чисел. – М.: «Высшая школа», 1962 г. - 260 с.
Никольский С.М. Алгебра7. учебник.- М.: « Просвещение», 1999г.–137с.
Сергеев И.Н. Примени математику.- М .: « Наука», 1990г.-с.63
Соловьев Ю. Неопределенные уравнения первой степени: Квант, 1992 г., №4.
Стройк Д.Я. Краткий очерк истории математики. – М.: «Наука», 1990
:http // student7.ru/greeceOld/n/math8.
http://www.tutoronline.ru/blog/zadacha-diofanta
http://otherreferats.allbest.ru/mathematics/
Шевкин А.В. «Задача С6»_М:Экзасен, 2011
Садовничий Ю.В, «Задачи и уравнения в целых числах»-М:Экзасен, 2017
Школьная энциклопедия. Математика. / под редакцией Никольский С. М. – Москва: Издательство «Большая российская энциклопедия», 1996 – с.648.
Энциклопедия для детей Т. 11 (Математика) / под редакцией М. Д. Аксёнова – Москва: Издательство «Аванта +», 1998 – с.688.
Энциклопедический словарь юного математика / под редакцией Гнеденко Б. В. – Москва: Издательство «Педагогика», 1985 – с. 350.
Бабинская И. Л. Задачи математических олимпиад. – Москва, 1875.
Болгарский Б. В. Очерки по истории математики. –Минск, 1979.
Васильев Н. Б., Егоров А. А. Задачи Всесоюзных математических олимпиад. – Москва, 1998.
Васильев Н. Б., Тутенмахер В. Л. Заочные математические олимпиады. – Москва, 1986.
Выгодский М. Я. Справочник по элементарной математике. – Москва, 1974.
Гальперин Г. А., Тольпыго А. К. Московские математические олимпиады. – Москва, 1986.
Генкин С. А., Интенберг И. В., Фомин Д. В. Ленинградские математические кружки. – Киров, 1994.
Егоров А. А. О дискриминанте. – Приложение к журналу «Квант», № 2/1994. с – 117.
Задачи математических олимпиад школьников Нижегородской области. – Н. Новгород, 1998.
Заочные математические олимпиады. – Москва, 1981.









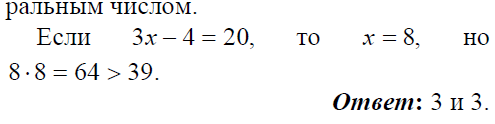


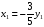 , у1 кратно 5, т.е. у1 =5n, х1 = -3n, где n- любое целое число, вернёмся к старым неизвестным х-2= -3n , х= 2-3n,
, у1 кратно 5, т.е. у1 =5n, х1 = -3n, где n- любое целое число, вернёмся к старым неизвестным х-2= -3n , х= 2-3n, хлебов. Составим уравнение
хлебов. Составим уравнение  .
.



















