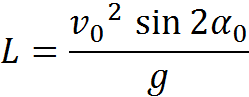Проект "Бросание мячика в стенку" на языке Visual Basic
Создадим сначала графический интерфейс проекта "Бросание мячика в стенку"
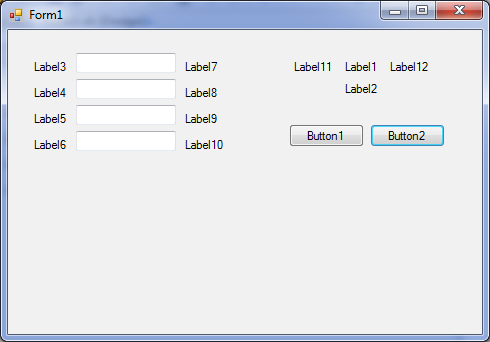
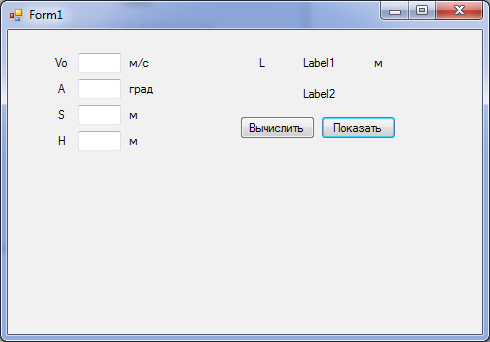
1. Разместить на форме:
- четыре текстовых поля для ввода значений:
TextBox1 - начальной скорости
TextBox2 - угла бросания мячика
TextBox3 - расстояние до стенки
TextBox4 - высота стенки
- надпись Label1 для вывода высоты мячика на заданном расстоянии;
- надпись Label2 для вывода текстового сообщения о результатах броска;
- десять надписей для вывода имён переменных и единиц измерения;
- кнопку Button1 для запуска событийной процедуры вычисления результатов бросания мячика;
- кнопку Button2 для демонстрации траектории движения мячика.
Обработчик события - вычисление результатов бросания мячика
2. Создать программный код обработчика события, который определяет попадание мячика в стенку. В этом коде:
- объявить вещественные константы одинарной точности G (ускорение свободного падения g) и Pi (число π);
- объявить вещественные переменные одинарной точности V0 (начальная скорость v0), А (угол бросания α), S (расстояние до стенки s), H (высота стенки h) и L (высота мячика l);
- присвоить переменным V0, A, S, H значения, введенные в текстовые поля, с использованием функции преобразования строки в вещественное число Val();
- вычислить высоту мячика L на заданном расстоянии по формуле.
- вывести высоту мячика L на надпись Label1;
- вывести текстовое сообщение о результатах броска на надпись Label2 с использованием оператора Select Case, в котором в качестве условия проверяется значение переменной L.
В языке программирования Visual Basic аргументы тригонометрических функций Sin(), Cos() и Tan() задаются в радианах, а угол бросания мячика мы будем вводить в градусах. Поэтому необходимо преобразовать значения углов из градусов в радианы с использованием константы Pi.
Код:
Const G As Single = 9.81
Const Pi As Single = 3.14
Dim V0, A, S, L, H As Single
Private Sub Button1_Click(...)
'Ввод начальных значений
V0=Val(TextBox1.Text)
A=Val(TextBox2.Text)
S=Val(TextBox3.Text)
H=Val(TextBox4.Text)
'Попадание в стенку
L=S*Math.Tan(A*Pi/180)-(G*S^2)/(2*V0^2*Math.Cos(A*Pi/180)^2)
Label1.Text=L
Select Case L
Case Is
Label2.Text="Недолет"
Case Is H
Label2.Text="Перелет"
Case Else
Label2.Text="Попадание"
End Select
End Sub
Обработчик события - демонстрация траектория движения мячика
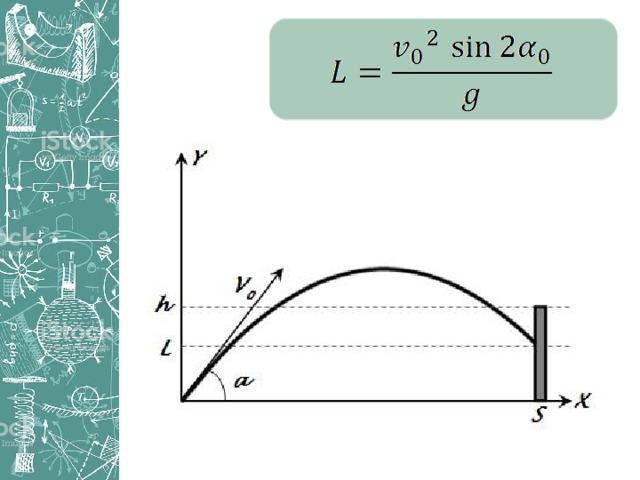
Для визуализации компьютерной модели построим в графическом поле траекторию движения мячика.
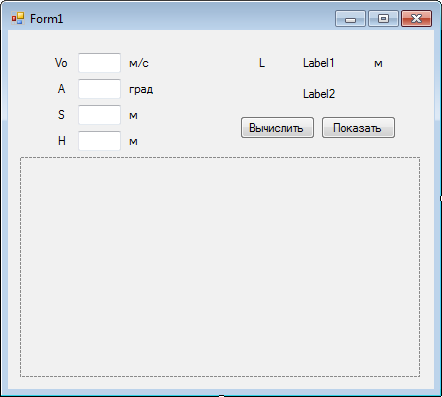
3. Поместить дополнительно на форму графическое поле PictureBox1. С помощью диалогового окна Свойства установить с использованием свойства Size размер поля, например 400; 220.
В обработчике события осуществим преобразование компьютерной системы координат графического поля в математическую систему координат, удобную для построения траектории движения. Нарисуем оси координат и нанесем на них шкалы.
4. В математической системе координаты находятся в диапазонах 0 - координаты точек графика необходимо умножить на 10;
- значения шкал осей разделить на 10.
Построение траектории осуществить в цикле со счетчиком (координата Х) с использованием метода рисования точки DrawEllipse(Pen1, X*10, Y*10, 1, 1), в котором координатами точки являются координаты мячика.
Код:
Dim Graph1 As Graphics
Dim Pen1 As New Pen(Color.Black, 4)
Dim drawBrush As New SolidBrush(Color.Black)
Dim drawFont As New Font("Arial",10)
Dim X, Y, T As Single
Private Sub Button2_Click(...)
Graph1=Me.PictureBox1.CreateGraphics()
Graph1.Clear(Color.White)
'Печать шкал математической системы координат
'в компьютерной системе координат
For X=0 To 400 Step 50
Graph1.DrawString (X/10, drawFont, drawBrush, X, 200)
Next X
For Y=20 To 220 Step 50
Graph1.DrawString((Y-20)/10, drawFont,drawBrush, 0, 220-Y)
Next Y
'Преобразование компьютерной системы координат
'в математическую систему координат
Graph1.ScaleTransform(1,-1)
'Поворот оси Y
Graph1.TranslateTransform(0,-200)
'Сдвиг по оси Y
'Рисование осей математической системы координат
Graph1.DrawLine(Pen1, 0, 0, 400, 0) 'Ось X
Graph1.DrawLine(Pen1, 0, -20, 0, 200) 'Ось Y
'Построение траектории движения мячика
For T=0 To 10 Step 0.1
Y=V0*Math.Sin(A*Pi/180)*T-G*T*T/2
X=V0*Math.Cos(A*Pi/180)*T
Graph1.DrawEllipse(Pen1,X*10,Y*10,1,1)
Next T
End Sub
Компьютерный эксперимент. Введём произвольные значения начальной скорости и угла бросания мячика. Скорее всего, попадания в стенку не будет. Меняя один из параметров, например угол, произведем пристрелку, используя известный артиллерийский приём "взятие в вилку", в котором применяется эффективный метод "деление пополам". Сначала найдём угол, при котором мячик не долетит до стенки. Вычислим среднее значение углов, составляющих "вилку", и проверим попадает ли при этом значении мячик в стенку. Если он попадает в стенку, то задача выполнена, если не попадает, то рассмотрим новую "вилку" и т.д.
5. Запустить проект и ввести значения начальной скорости, угла бросания, расстояния до стенки и её высоты. Щёлкнуть по кнопкам Вычислить и Показать. На надписи будут выведены результаты, а в графическом поле появится траектория движения тела.
Подобрать значения начальной скорости и угла бросания мячика, обеспечивающие его попадание в стенку.
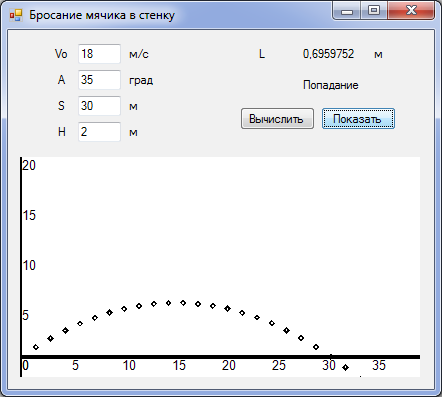
Например, при скорости бросания мячика v0=18 м/с и угле бросания α=35° мячик попадает в стенку высотой h=2 м и находящуюся на расстоянии s=30 м на высоте l=0,6959749 м.
Анализ результатов. Полученная точность высоты попадания мячика в стенку l=0,6959749 м не имеет физического смысла и определяется типом переменной. Так как L является переменной одинарной точности, то её значение вычисляется с точностью семи значащих цифр. Исходные данные заданы с точностью две значащие цифры, поэтому необходимо и результат округлить до двух значащих цифр: l=0,70 м.
Корректировка модели. Рассмотренный выше проект "Бросания мячика в стенку" позволяет задавать различные значения скорости и угла бросания мячика. Предположим, что броски мячика производятся с одинаковой скоростью, и попробуем определить диапазон углов, при которых происходит попадание мячика в стенку.
Для этого необходимо в цикле со счетчиком по углу бросания вычислить положение мячика на расстоянии стенки и определить те углы, которые соответствуют высоте стенки.











 униципальное казённое общеобразовательное учреждение
униципальное казённое общеобразовательное учреждение 
 =X
=X