Индивидуальный образовательный проект по дисциплине «Математика» на тему: «Параллельное проектирование..»

ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ ПРИМОРСКОГО КРАЯ

краевое государственное бюджетное

профессиональное образовательное учреждение «Автомобильно-технический колледж»

Индивидуальный образовательный проект

по дисциплине «Математика»

на тему: «Параллельное проектирование..»

Выполнил студент Шамовцев Денис Анатольевич, 27 группа,

Профессия 23.01.03 «Автомеханик»

Руководитель: преподаватель Каралупова В.Б.

пгт. Ярославский

2019г.

ВВЕДЕНИЕ

Геометрия, наравне со многими другими разделами математики, дает возможность почувствовать красоту математики вообще и может стать для кого-то началом пути в «большую науку». Кроме того, каждый любитель геометрии имеет шанс открыть нечто новое и пополнить ее сокровищницу собственной драгоценной находкой, ибо геометрия поистине неисчерпаема!

А. Г. Мякишев «Элементы геометрии треугольника»

Геометрия многолика. И одну задачу можно решить большим количеством разных способов. В школе изучается лишь малая часть того, что принято называть геометрией. Моя работа называется «Помогает параллельное проектирование». Работа показывает, что параллельное проектирование позволяет не только строить проекции фигур и пространственных тел, но еще и облегчает решение ряда задач, связанных с нахождением отношений отрезков и нахождения отношения площадей.

В этой работе рассмотрен удивительный способ для решения ряда задач. Способ, не описанный в школьном учебнике. Способ, основанный на свойствах параллельного проектирования таких как: любой треугольник при помощи параллельного проектирования можно перевести в правильный; при параллельном проектировании сохраняются отношения отрезков и площадей фигур.

Работа состоит из двух частей. В первой части работы рассказывается, что же такое параллельное проектирование, формулируются и доказываются некоторые его свойства. Во второй – практической части рассмотрен ряд задач, которые можно решать с помощью параллельного проектирования.

К сожалению, параллельное проектирование очень редко используется. Оно не упоминается в школьной программе до десятого класса, хотя оно могло бы существенно упростить решение некоторых задач по геометрии. К тому же я считаю эту тему очень интересной и стоящей, ведь мы встречаемся с параллельным проектированием каждый день.

Актуальность: Внимание в этой работе направлено на связь курсов математики и черчения, так как изучение математики, точнее стереометрии значительно отражается на изучении начертательной геометрии – одного из разделов инженерной графики, которая в дальнейшем будет являться моим спецпредметом: умение аккуратно и красиво чертить, правильно изображать пространственные фигуры на плоскости, использовать свойства параллельной и ортогональной проекций и свойства площадей и объемов при решении реальных прикладных задач

. Цель исследования: параллельное проектирование и его свойств, а также применение параллельного проектирования при решении задач.

Методы исследования:

1. Изучение теории по параллельному проектированию

2. Доказательство некоторых свойств параллельного проектирования

3. Установление связи между параллельным проектированием и решением задач

Задача – использовать знания о параллельной и ортогональной проекции и их свойствах, полученные на уроках математики, для более полного и глубокого усвоения программного материала по начертательной геометрии.

Гипотеза: Можно предположить, что параллельное проектирование, изучаемое на уроках стереометрии может в дальнейшем применяться на занятиях по черчению и при работе над прикладными задачами .

1. ЧТО ТАКОЕ ПАРАЛЛЕЛНОЕ ПРОЕКТИРОВАНИЕ

Ветреный летний день.

Прижавшиеся к стене

Дерево и его тень.

И тень интересней мне.

Иосиф Бродский. «Сидя в тени»

Пусть – π некоторая плоскость, l – пересекающая ее прямая (рис. 1). Через произвольную точку A, не принадлежащую прямой l, проведем прямую, параллельную прямой l. Точка пересечения этой прямой с плоскостью π называется параллельной проекцией точки A на плоскость π в направлении прямой l. Обозначим ее A'. Если точка A принадлежит прямой l, то параллельной проекцией A на плоскость π считается точка пересечения прямой l с плоскостью π.

математика параллельный проектирование

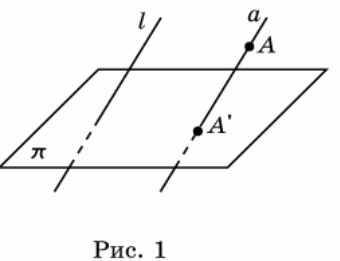
Таким образом, каждой точке A пространства сопоставляется ее проекция A' на плоскость π. Это соответствие называется параллельным проектированием на плоскость π в направлении прямой l.

Определение: Пусть Ф - некоторая фигура в пространстве. Проекции ее точек на плоскость π образуют фигуру Ф', которая называется параллельной проекцией фигуры Ф на плоскость π в направлении прямой l. Говорят также, что фигура Ф' получена из фигуры Ф параллельным проектированием.

Мы не раз встречались с параллельным проектированием в жизни. Например, наша тень в солнечный день на ровном асфальте есть наша параллельная проекция ( солнечные лучи приближенно можно считать параллельными ввиду большой удалённости Солнца от Земли).

Параллельное проектирование позволяет получать наглядные изображения пространственных (трёхмерных) фигур на (двумерной) плоскости (рис. 4). Дело в том, что параллельное проектирование сохраняет ряд важных черт изображаемой фигуры. Перечислим основные свойства параллельного проектирования в предложении, что направление проектирования не параллельно рассматриваемым прямым и отрезкам (в противном случае их проекциями являются точки.

  В стереометрии изучаются пространственные фигуры, однако на чертеже они изображаются в виде плоских фигур. Каким же образом следует изображать пространственную фигуру на плоскости? Обычно в геометрии для этого используется параллельное проектирование.
    Пусть p - некоторая плоскость, l - пересекающая ее прямая (рис. 1). Через произвольную точку A, не принадлежащую прямой l, проведем прямую, параллельную прямой l. Точка пересечения этой прямой с плоскостью p называется параллельной проекцией точки A на плоскость p в направлении прямой l. Обозначим ее A'. Если точка A принадлежит прямой l, то параллельной проекцией A на плоскость p считается точка пересечения прямой l с плоскостью p.

   Таким образом, каждой точке A пространства сопоставляется ее проекция A' на плоскость p. Это соответствие называется параллельным проектированием на плоскость p в направлении прямой l.
    Пусть Ф - некоторая фигура в пространстве. Проекции ее точек на плоскость p образуют фигуру Ф', которая называется параллельной проекцией фигуры Ф на плоскость p в направлении прямой l. Говорят также, что фигура Ф' получена из фигуры Ф параллельным проектированием.

3.7. Ортогональное проектирование

О пределение 3.10. 

Параллельное проектирование, при котором проектирующие прямые перпендикулярны к плоскости проекций, называется ортогональным проектированием.

Т еорема 3.13. 

Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции: 

Теоремы о проекциях (с доказательством)

  Свойство 1. Если прямая параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.
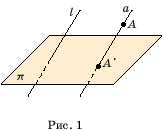
    Доказательство. Ясно, что если прямая k параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой на плоскость p будет точка пересечения прямой l и плоскости p. Пусть k не параллельна и не совпадает с прямой l (рис. 2). Возьмем какую-нибудь точку A на прямой k и проведем через нее прямую a, параллельную l. Ее пересечение с плоскостью проектирования p даст точку A', являющуюся проекцией точки A. Через прямые a и k проведем плоскость a . Ее пересечением с плоскостью p будет искомая прямая k', являющаяся проекцией прямой k.

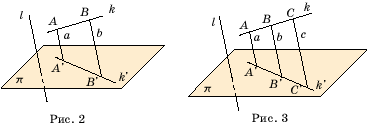
    Свойство 2. Проекция отрезка при параллельном проектировании есть точка или отрезок, в зависимости от того лежит он на прямой, параллельной или совпадающей с прямой l, или нет. Параллельное проектирование сохраняет отношение длин отрезков, лежащих на прямой, не параллельной и не совпадающей с прямой l. В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.
    Доказательство.Ясно, что если отрезок лежит на прямой, параллельной или совпадающей с прямой l, то его проекцией будет точка. Пусть точки A, B и C лежат на прямой k, не параллельной и не совпадающей с прямой l; k' – проекция прямой k на плоскость p в направлении прямой l; A', B', C' – проекции точек A, B и Cсоответственно; a, b, c – соответствующие прямые, проходящие через эти точки и параллельные прямой l (рис. 3). Тогда из теоремы Фалеса планиметрии следует равенство отношений AB : BC = A'B' : B'C'. В частности, если точка B - середина отрезка AC, то B' - середина отрезка A'C'.
    Свойство 3. Если две параллельные прямые не параллельны прямой l, то их проекции в направлении l могут быть или параллельными прямыми или одной прямой.
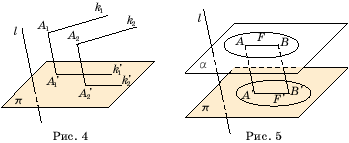
    Доказательство. Пусть k₁, k₂ - параллельные прямые, не параллельные прямой l. Так же как и при доказательстве первого свойства, рассмотрим плоскости a₁, a₂, линии пересечения которых с плоскостью p дают проекции k₁', k₂' прямых k₁, k₂ соответственно (рис. 4). Если плоскости a₁ и a₂ совпадают, то проекции прямых k₁ и k₂также совпадают. Если эти плоскости различны, то они параллельны между собой, по признаку параллельности плоскостей (прямая k₁ параллельна прямой k₂, прямаяA₁A₁' параллельна прямой A₂A₂' ). В силу свойства параллельных плоскостей, линии пересечения этих плоскостей с плоскостью p параллельны.

   При изображении пространственных фигур на плоскости особенно важно уметь правильно изображать плоские фигуры, поскольку они входят в поверхность основных пространственных фигур. Например, плоские многоугольники являются гранями многогранников, круги - основаниями цилиндров и конусов.
    Теорема. Если плоская фигура F лежит в плоскости, параллельной плоскости проектирования p, то ее проекция F' на эту плоскость будет равна фигуре F.
    Доказательство. Пусть A, B – точки фигуры F и A’, B’ – их параллельные проекции (рис. 5). Тогда ABB’A’ – параллелограмм. Поэтому параллельный перенос на вектор 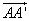  переводит точку B в B’. Поскольку точку B фигуры F можно выбирать произвольно, то этот параллельный перенос переводит фигуру F в фигуру F’. Значит фигуры F и F’ равны.

2.СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕКТИРОВАНИЯ

Свойство 1. Проекция прямой есть прямая, проекция отрезка – отрезок.

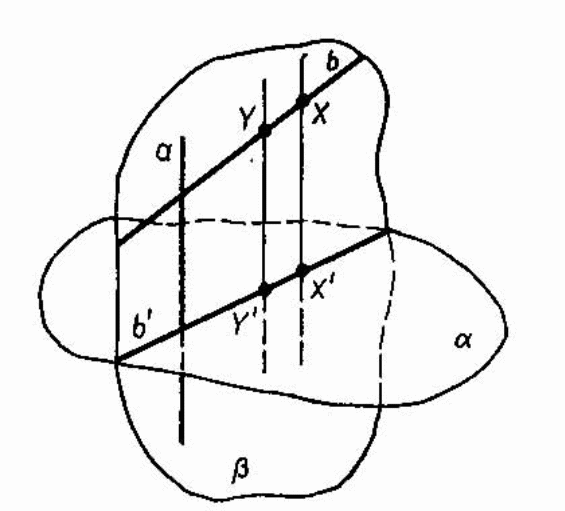
Свойство 2. Две параллельные прямые проектируются либо в две параллельные прямые, либо в одну и ту же прямую. Проекции параллельных отрезков лежат либо на параллельных прямых, либо на одной прямой.

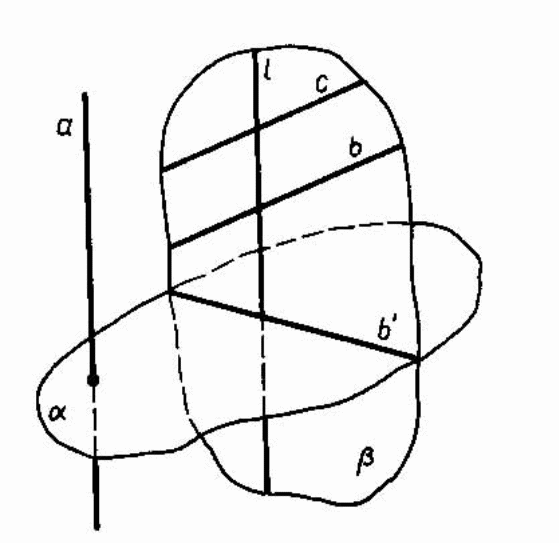
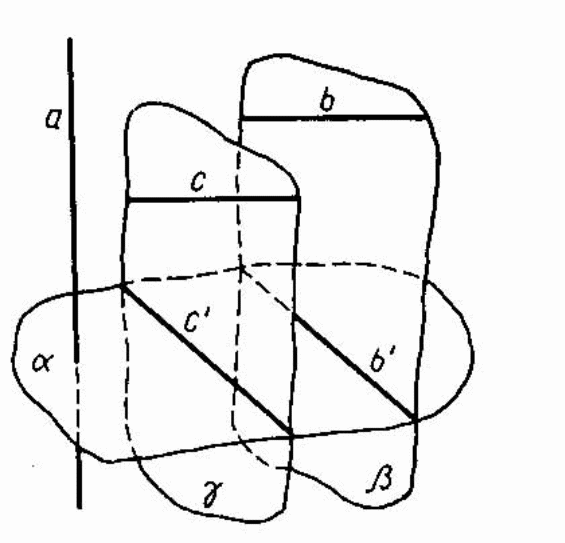
Свойство 3. Длины проекций параллельных отрезков или отрезков лежащих на одной прямой, пропорциональны длинам этих отрезков

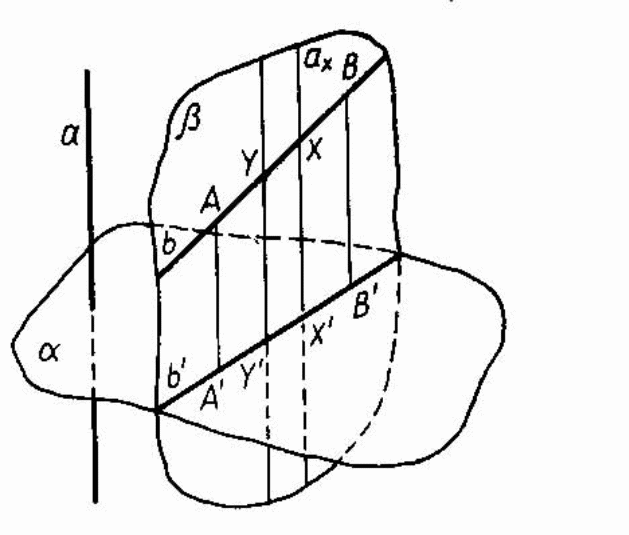
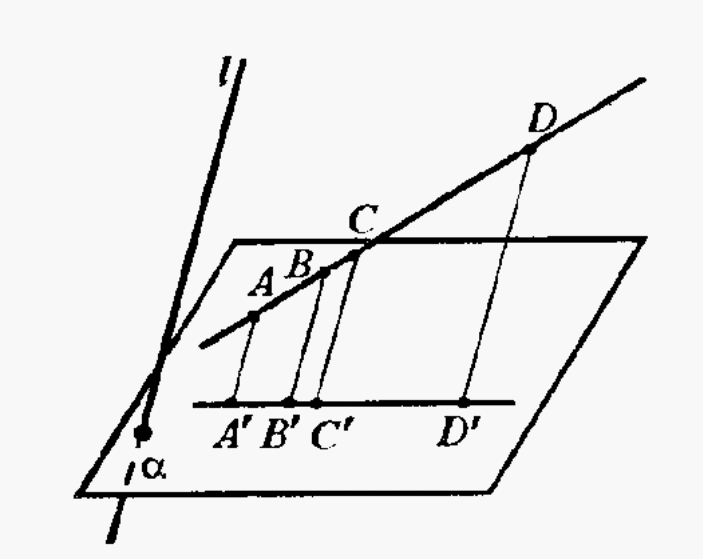
Доказательство свойства №3. Пусть АВ и СD – отрезки не параллельные направлению проектирования l ; А`, B`, C`, D` - проекции точек А, В, С, D соответственно на плоскость а в направлении l . Если А` B` и C` D` - один и тот же отрезок, то АВ = СD и доказываемое утверждение очевидно. Пусть А` B` и C`D`различны. Рассмотрим сначала случай, когда проектируемые отрезки лежат на одной прямой (рис. 10). Тогда их проекции лежат на линии пересечения плоскости а и плоскости, проходящей через прямую АВ параллельно направлению проектирования l. Применяя известную теорему о пропорциональных отрезках, получим, что АВ :CD = A` B` : C` D`.

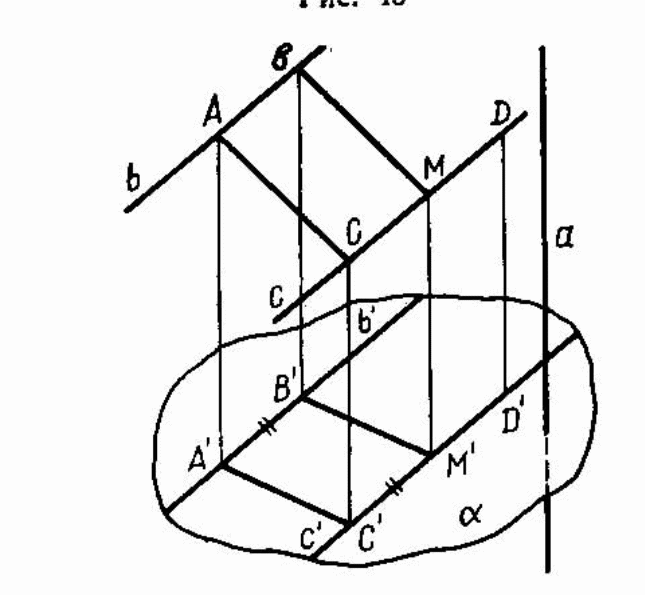
Теперь рассмотрим случай, когда отрезки АВ и СD параллельны, а их проекции различны (рис. 11). Возьмём на продолжении отрезка СD за точку С точку Е такую, что СЕ = АВ. Так как (СЕ) ll (AB), но четырёхугольник АВЕС – параллелограмм в плоскости, проходящей через прямые АВ и СD ( по признаку параллелограмма), следовательно, (АС) ll (BE). Пусть Е` - проекция точки Е на плоскость а в направлении l. По свойству №2 (A` C`) ll (B` E`) и (A` B`) ll (C` E`) ( так как (АС) ll (BE) и (АВ) ll (CE)), но (A`B`) ll (C`D`), значит, Е` принадлежит (C`D`) и, так как A`B`E`C` - параллелограмм, А`B` = C`E`. Итак равенство АВ : СD = A`B` : C`D` равносильно равенству СЕ : ЕD = A`B` : C`D`, тем самым мы свели рассматриваемый случай к разработанному выше.

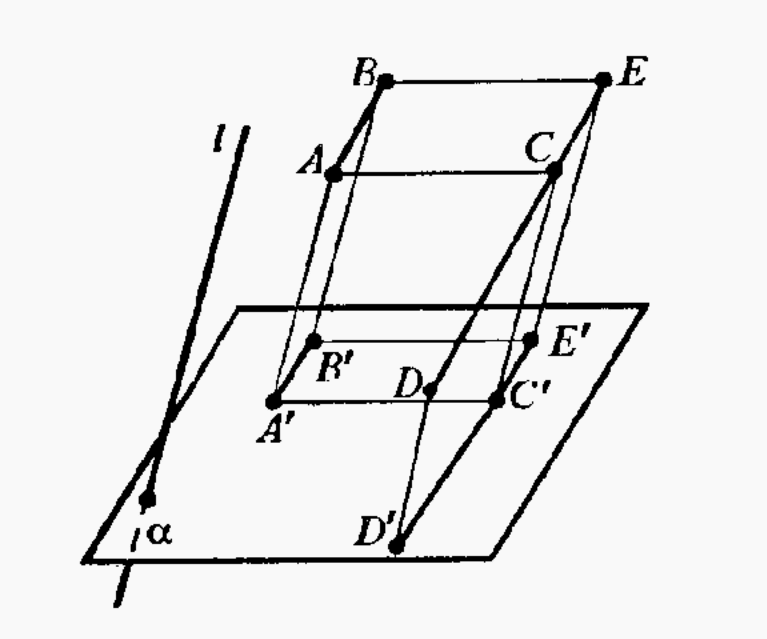
Свойство 4. При параллельном проектировании сохраняется отношения площадей двух любых фигур, если направление проектирования не параллельно плоскостям фигур.

Свойство 5. Любой треугольник можно рассматривать как параллельную проекцию данного треугольника с точностью до подобия.

Доказательство свойства 5: Докажем, что в общем случае треугольник любой формы может служить параллельной проекцией равностороннего треугольника.

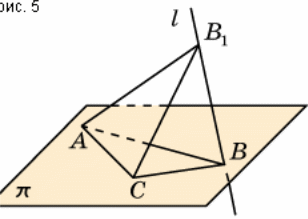
Действительно, пусть дан произвольный треугольник ABC в плоскости π Построим на одной из его сторон. например, AC равносторонний треугольник AB1C так, чтобы точка B1 не принадлежала плоскости π. Обозначим через l прямую, проходящую через точки B1 и B. Тогда ясно, что треугольник ABC является параллельной проекцией треугольника AB1C на плоскость π в направлении прямой l.

3. Решение задач с использованием параллельного проектирования

Задача 1. Доказать, что прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжений ее боковых сторон, делит основания трапеции пополам.

Решение: Изобразим на плоскости β (рис. 11) и мысленно параллельно спроектируем его на плоскость α так, чтобы треугольник AMD перешел в A1M1D1 равнобедренный треугольник (рис.12).

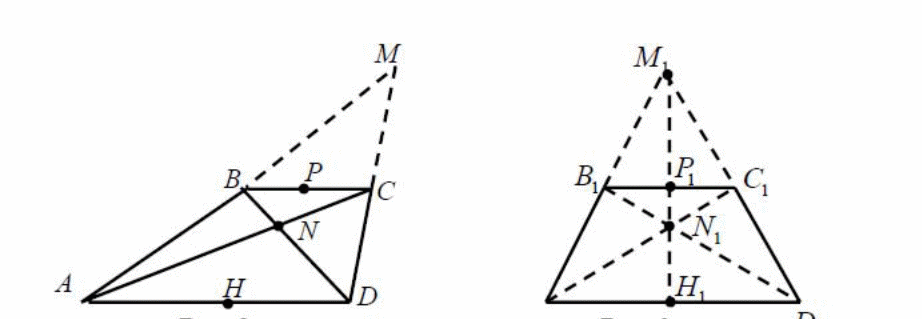
Из свойств параллельного проектирования следует, что проекцией трапеции ABCD является трапеция A1B1C1D1, то есть B1C1 // A1D1. Далее, так как треугольник A1M1D1 равнобедренный, то его высота M1H1 совпадает с медианой и является осью симметрии треугольника.

При симметрии относительно прямой M1H1 точка A1 переходит в точку D1, поэтому прямая A1M1 переходит в прямую D1M1 , а прямая B1C1 переходит в себя, так как она перпендикулярна оси симметрии.

Следовательно, точка C1 переходит в точку B1, прямая A1C1 переходит в прямую B1D1, а поэтому N1 точка пересечения прямых A1C1 и B1D1 находится на оси симметрии, то есть на прямой M1H1.

В результате доказано, что для трапеции точка пересечения диагоналей, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой. Поэтому при обратном параллельном проектировании трапеции A1B1C1D1 в трапецию ABCD точки M1, P1, N1, H1 , лежащие на одной прямой, проектируются соответственно в точку M пересечения прямых AB и CD, в точку P – середину основания BC, в точку N пересечения диагоналей AC и BD и в точку H – середину основания AD, причем точки M, P, N, H также лежат на одной прямой.

Что и требовалось доказать.

Задача 2..Рассмотрим параллельную проекцию правильного шестиугольника ABCDEF с центром в точке O (точка O – точка пересечения диагоналей правильного шестиугольника). Выполнить рисунок.

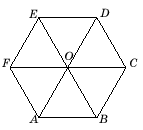
Выберем какой-нибудь треугольник, например, AOB. Его проекцией может быть треугольник A'O'B' на плоскости π, имеющий произвольную форму. Выполнить рисунок.

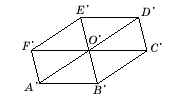
- Далее отложим O'D'=A'O' и O'E'=B'O'.

- Теперь из точек A' и D' проведем прямые, параллельные прямой B'O';

- из точек B' и E' проведем прямые, параллельные прямой A'O'.

-Точки пересечения соответствующих прямых обозначим F' и C'.

- Шестиугольник A'B'C'D'E'F' и будет искомой проекцией правильного шестиугольника ABCDEF. 

Задача 3. Треугольник ABC является параллельной проекцией треугольника AB₁C на плоскость π в направлении прямой l. Выполнить рисунок.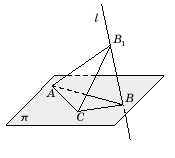

Задача 4. На диагонали АС1 параллелепипеда АВСDA1B1C1D1 Взята точка М, а на прячка N так, что отрезки MN и DB параллельны. Найти их отношение. А А1 D1 C1 B1 B C D М N Решение: 1. Построим проекцию параллелепипеда на плоскость, перпендикулярную прямой В1С. плоскости боковой грани, а В1С как диагонали квадрата., а D1C1ВС1 В1С.следовательно D1C1 Т.е мы проектируем наш параллелепипед на плоскость D1C1ВА в направлении В1С. Эта проекция представляет собой два равных параллелограмма АВВ1А1 и DCC1D1 с общей стороной А1В1=DC, где MN // BD. (По свойству проектирования параллельные прямые перешли в параллельные прямые). 2) MN=DK Т.к. ∆A1KА = ∆С1МС по свойству (УСУ) 3) ВK=2MN Т.к. ∆ КС1В подобен ∆ МС1С по двум углам (угол МС1N и угол KC1В – общий, а углы МСС1 и КBC1 равны как соответственные при параллельных MN // BК и секущей С1В ) 4). Из 2 и 3

следует, что BD=3MN.

Задача 5. Плоское изображение, подчиняясь определенным законам, способно передать впечатления о трехмерном предмете

В живописи существует целое направление, которое называется «импоссибилизм» (невозможность) - изображение невозможных фигур, парадоксов. Известный голландский художник Мариус Эшер в гравюрах «Бельведер», «Водопад» изобразил невозможные объекты

Современный шведский архитектор Оскар Рутерсвард посвятил невозможным объектам серию своих художественных работ

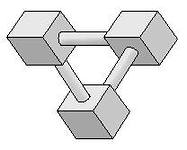
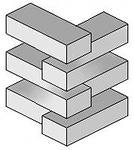
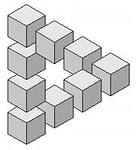
Обобщая, делаем вывод, что грамотно выполненный чертеж – качественная помощь при решении любой геометрической задачи.

ЗАКЛЮЧЕНИЕ

Анализ теоретического материала по параллельному проектированию позволил узнать свойства и область применения параллельного проектирования. 2. Решение практических задач показало, что многие задачи, даже очень сложные можно решить с помощью параллельного проектирования, сэкономив при этом и время, и силы. 3. Я узнала много нового и интересного, работая над данной темой. Многие задачи оказываются не такими трудными, как казалось бы. Это действительно занимательно и увлекательно. Так же эта прекрасная тема пригодится мне в будущем, при изучении стереометрии в старших классах. Заключение. В заключении мне хотелось бы повторить слова эпиграфа Геометрия …, наравне со многими другими разделами математики, дает возможность почувствовать красоту математики вообще и может стать для когото началом пути в «большую науку». Кроме того, каждый любитель геометрии … имеет шанс открыть нечто новое и пополнить ее сокровищницу собственной драгоценной находкой, ибо геометрия поистине неисчерпаема! А. Г. Мякишев «Элементы геометрии треугольника»

1. Анализ теоретического материала по параллельному проектированию позволил узнать свойства и область применения параллельного проектирования.

2. Решение практических задач показало, что многие задачи, даже очень сложные можно решить с помощью параллельного проектирования, сэкономив при этом и время, и силы.

3. Я узнал много нового и интересного, работая над данной темой. Многие задачи оказываются не такими трудными, как казалось бы. Это действительно занимательно и увлекательно.

СПИСОК ЛИТЕРАТУРЫ

1. А. Ю. Калинин, Д. А. Терешин. «Стереометрия 10». МФТИ 1996.

2 А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. «Неожиданный шаг или сто тринадцать красивых задач». Киев, Агрофирма «Александрия» 1993.

3. Геометрия 10-11 класс - Л.С. Атанасян. «Просвещение», 2001. Азмеще

4. Аргунов Б. И., Балк М, Б. Геометрические построения на плоскости. 2-е изд. М.: Учпедгиз, 1957.

5. Казаков П. Г. Параллельные проекции и методы и решения конструктивных задач. М.: Учпедгиз, 1960

6. Орехов П. С. Изображения в стереометрии. Ижевск: Удмуртия, 1981.

7. Четверухин Н. Ф. Изображения в курсе геометрии. М.: Учпедгиз, 1958.

8. Четверухин Н. Ф. Методы геометрических построений. М.: Учпедгиз, 1952