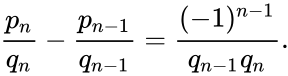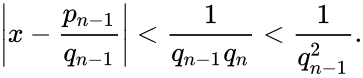Просмотр содержимого документа
«Доклад на тему "конечные и бесконечные цепные дроби"»
|
|
|
|
|
| Доклад |
| КОНЕЧНЫЕ И БЕСКОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ
|
|
| Учитель: Горчева К.А. |
|
|
|
|
|
Пермь, 2022 г.
Конечные и бесконечные цепные дроби
Непрерывная дробь (или цепная дробь) — это конечное или бесконечное математическое выражение вида
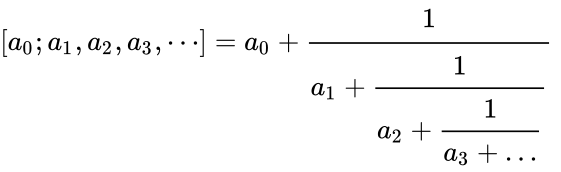
где 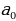 есть целое число, а все остальные
есть целое число, а все остальные 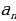 — натуральные числа (положительные целые). При этом числа
— натуральные числа (положительные целые). При этом числа 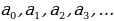 называются неполными частными или элементами цепной дроби.
называются неполными частными или элементами цепной дроби.
Любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной). Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально.
Главное (но далеко не единственное) назначение непрерывных дробей состоит в том, что они позволяют находить хорошие приближения вещественных чисел в виде обычных дробей. Непрерывные дроби широко используются в теории чисел и вычислительной математике, а их обобщения оказались чрезвычайно полезны в математическом анализе и других разделах математики. Используются также в физике, небесной механике, технике и других прикладных сферах деятельности.
Алгоритм разложения вещественного числа на цепную дробь имеет следующий вид:
| 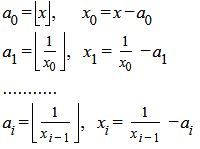 . .
|
Если на i-ом шаге xi=0, то процесс останавливается. Цепная дробь принимает вид:
| 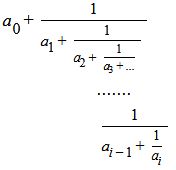 . .
|
Теорема. Всякое действительное число может быть разложено в цепную дробь единственным образом, и всякая конечная или бесконечная цепная дробь имеет своим значением некоторое действительное число.
Пусть α ∈ R - действительное число, заключенное между двумя последовательными целыми числами: а ≤ α а + 1. Число а будем называть нижним целым числа α (это просто целая часть α ), а число а + 1 - верхним целым. Обозначениями для нижнего и верхнего целого числа α пусть будут, соответственно, ⎣ α ⎦ и ⎡ α ⎤. Возьмем произвольное действительное число α ∈ R, q1 = ⎣ α ⎦. Тогда α = q 1 + β1, 0 ≤ β1 1, следовательно α1 =1/β1 1, и
α = q1 +1/α2. Если, далее, α1 – не целое, то снова: q2 = ⎣ α2 ⎦,
α2 = q2 + β2 = q2 + 1/α3, α3 1, и α = q1 +1/q2 + 1/α3. Продолжая этот процесс взятия нижних целых и переворачивания дробных частей, получим запись произвольного числа α ∈ R в виде цепной дроби.
Пример. Разложить 105/38 в цепную дробь.
Используем алгоритм Евклида:
105 = 38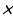 2 + 29
2 + 29
38 = 29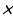 1 + 9
1 + 9
29 = 9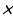 3 + 2
3 + 2
9 = 2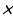 4 + 1
4 + 1
2 = 1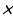 2
2
Неполные частные подчеркнем потому, что теперь для написания ответа нужно расположить их подряд на этажах цепной дроби перед знаками плюс:
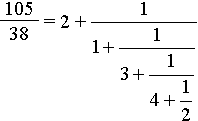 .
.
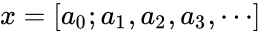 Подходящие дроби
Подходящие дроби
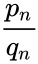 n
n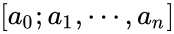 -ой подходящей дробью для цепной дроби называется конечная цепная дробь , значение которой равно некоторому рациональному числу . Подходящие дроби с чётными номерами образуют возрастающую последовательность, предел которой равен x. Аналогично, подходящие дроби с нечётными номерами образуют убывающую последовательность, предел которой также равен x.
-ой подходящей дробью для цепной дроби называется конечная цепная дробь , значение которой равно некоторому рациональному числу . Подходящие дроби с чётными номерами образуют возрастающую последовательность, предел которой равен x. Аналогично, подходящие дроби с нечётными номерами образуют убывающую последовательность, предел которой также равен x.
Эйлер вывел рекуррентные формулы для вычисления числителей и знаменателей подходящих дробей:
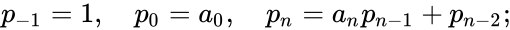
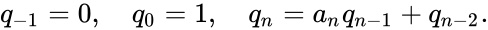
Таким образом, величины pn и qn представляются значениями континуант:
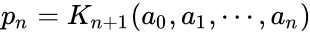
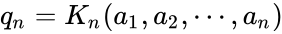
Последовательности {pn} и {qn} являются возрастающими.
Числители и знаменатели соседних подходящих дробей связаны соотношением
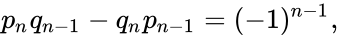
которое можно переписать в виде
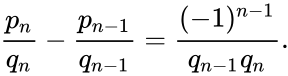
Откуда следует, что
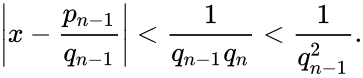






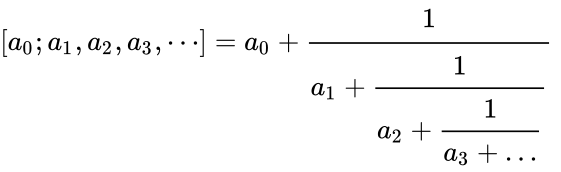
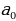 есть целое число, а все остальные
есть целое число, а все остальные 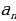 — натуральные числа (положительные целые). При этом числа
— натуральные числа (положительные целые). При этом числа 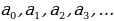 называются неполными частными или элементами цепной дроби.
называются неполными частными или элементами цепной дроби.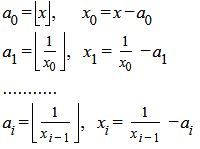 .
.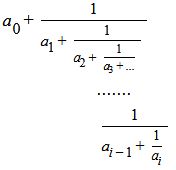 .
.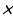 2 + 29
2 + 29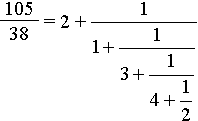 .
.